Rep:Mod:CW4013MGO

Abstract

A ccp MgO lattice was simulated using GULP software to probe the relative accuracies of the Quasi-harmonic approximation and Molecular Dynamics methods in simulating thermal expansion. Thermal Expansivities of 31.2 10^-6 T^-1 and 28.2 10^-6 T^-1 were determined for the simulations, displaying close accordance to literature at temperatures of 300 K and 260 K respectively. MD simulations have been shown to be more accurate at determining lattice volumes at low temperature, whilst the QHA achieves greater thermal expansivity accuracy over the 300 K to 1000 K range.

Introduction

The conventional (white line) and primitive (black line) unit cell, along with the labelled lattice parameters a = b = c. Bond angles are also labelled (not shown: γ)

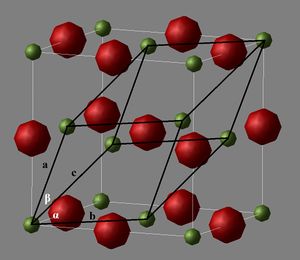
Computation provides a convenient way to study 3D crystal lattices and can be used to both model systems using empirical inputs or predict phenomena from a theoretical basis (ab initio methods). In any case, predictions may be made about the physical properties of solids, such as Magnesium(ii) oxide (MgO), a cubic close packed (ccp) lattice consisting of one atom type at every lattice point (O^2-) arbitrarily chosen for this experiment) and the other atom type (Mg²⁺) occupying every octahedral hole per unit cell. MgO expansion has been studied particularly within the geophysics disciplines due to the abundance of MgO in the Earth's mantle and the effect it has on the convections therein.

General Utility Lattice Program

GULP is a software package used to simulate solid materials based on a broad range of potentials and calculate the properties thereof. Due to being an ionic lattice, the solid may be modeled classically using a potential surface, the components of which include a Coulombic and a Morse-like interatomic potential (such as a Buckingham potential) for this experiment. The Coulombic potential accounts for ion-ion attraction/repulsion according to Coulomb's law, the Buckingham potential adds ineratomic repulsion at low bond distances to prevent ions from making contact and 'sticking'. The aim is therefore to use classical simulations to model the quantum mechanical phenomenon of phonon vibrations (from a classical perspective) and to use the sum of all phonons to determine the Helmholtz free energy density of the lattice and hence predict some of the physical properties of the MgO lattice, such as the thermal expansivity (α).

The two methods used to obtain results were the Quasi-harmonic approximation (QHA) and molecular dynamics (MD) methods, both of which apply classical mechanics. These are discussed in more detail below.

Lattice vibrations

Phonons are defined as quantised vibrational modes of a lattice, treating the total vibration of a lattice as the sum of discrete, periodic elementary matter waves. the individual atoms vibrate independently yet in an ordered and coupled fashion assuming the phonons don't interact. The frequency of vibration for an infinite lattice (dispersion relation) is given by

${\omega }_k=\sqrt{\frac{4J}{M}}\sin \left(\frac{ka}{2}\right)$

where J is an elastic constant, M is atomic mass (for a system of identical atoms), k is a one-dimensional wavevector and a is the lattice parameter.

To describe the phonons of MgO, it's convenient to start from a linear chain of hydrogen atoms. Each repeating unit (Wigner-Seitz cell) centres on 1 atom with a lattice parameter (equivalent to bond distance in this case) of a. Transforming a into a* where $a*=\frac{2\pi }{a}$ results in a reciprocal lattice, with primitive unit cells corresponding to the first Brillouin zone defined from -π/a < k < π/a. Substituting k values into the dispersion relation yields matter waves of wavelength $\lambda =\frac{2\pi }{k}$, where peaks and troughs correspond to regions of high and low atomic density respectively at an instant in time. Note that as k tends to 0, the wavelength tends to infinity, corresponding to vibrations of all atoms in the same direction, whilst when k = ±π/a, λ = a/2, and every atomic pairing contains atoms oscillating against each other in opposite phase.

When the unit cell is extended to include two atoms, a similar dispersion relation is seen, but defined between -π/2a < k < π/2a instead, and ω 'cutting off' at half-maximum for the previous curve. A second band is seen; a result of extending the curve into the next cell in k-space and 'folding' the curve about the lines k = ±π/2a to afford two distinct bands, a lower 'acoustic' band and a higher 'optic' band with degeneracy at k = ±π/a. The acoustic band features vibrations between diatom pairs wherein the atoms of each pair oscillate in phase, and extends from λ = ∞ to λ = a. The higher band features all vibrations where the atoms in diatomic pairs oscillate out of phase with one another, with wavelengths between -a/2 and a. For MgO, degeneracy at k = ±π/2a is lost, and extending the model into three dimensions leads generates an additional four bands as will be explored.

Results and Discussion

Density of States and Dispersion Relation

The phonon dispersion relation ω(k) for MgO was plotted over 50 Npoints using a GULP calculation with 'calculate phonon eigenvectors' selected. Operationally, the software draws a conventional path through the Brillouin zone between symmetry points W to L, L to G, G to W, W to X and X to K, sampling 50 points in total along these lines. The bands in the graph represent the relationship between the phonon vibrational frequencies and their corresponding wavenumbers of vibration as discussed previously; 6 bands are visible in total for 2 atoms per Wigner-Seitz cell in 3 dimensions as expected; 3 acoustic-like bands are visible (one for each cartesian axis); an optical-like band is also visible. It is noted again that for the acoustic bands, Mg and O atoms move in phase with each other in their respective unit cells, whilst for the optic band, Mg and O oscillate in anti-phase with one another within each cell.

The phonon dispersion relation for MgO, displaying 6 unique branches with some degeneracy. The acoustic (low) and optic (high) branches are visible.

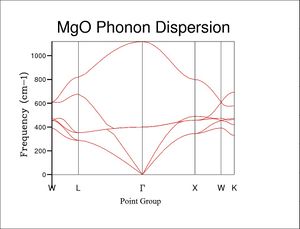
Where two branches merge into one, the density of states doubles, as two possible vibrations become possible for a given vibrational energy. This is illustrated by DOS GULP calculations (Phonon DOS GULP calculation, various grid sizes at default temperature and pressure).

The DOS for a single k-point L.

The Density of states for a 2x2x2 grid of k-points.

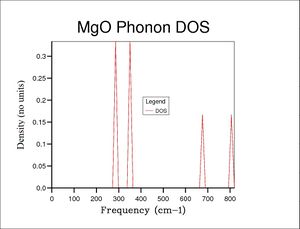
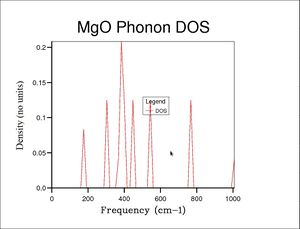
The DOS(ω) of MgO was plotted using GULP calculations, sampling phonons over various grid sizes (shrinking factors) to probe the minimum grid size required to obtain an accurate DOS graph. Algorithmically, the shrinking factor of nxnxn plots a matrix of n³ points on the Wigner-Seitz cell from the corner (defined by symmetry point L; k = 0.5a* + 0.5b* + 0.5c*) outwards. Therefore, a 1x1x1 grid size samples point L exclusively, corresponding to 6 longitudal matter waves 'pointing' in the L direction and oscillating at maximum energy. This becomes apparent when examining the DOS plot for the 1x1x1 grid size, where the peak frequencies map directly onto the dispersion graph at the L coordinate, noting that the peaks are twice as intense at frequencies where two dispersion branches have converged.

The Density of states for a 5x5x5 grid of k-points.

The Density of states for a 10x10x10 grid of k-points.

The Density of states for a 20x20x20 grid of k-points.

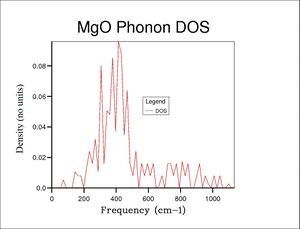
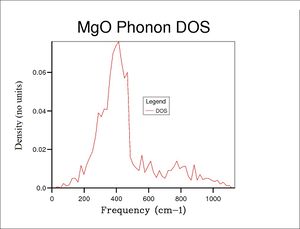
Applying a 2x2x2 grid leads to a DOS graph averaged over 8 points in reciprocal space, sampling 48 phonons. From grid size 5x5x5 upwards, the calculated zero-point energy of the lattice has converged and a dominant DOS peak is visible. Other peaks are obscured by noise however. By grid size 10x10x10, a smaller secondary peak is visible, and by 20x20x20, the signal:noise ratio is high enough to reveal all distinct peaks (the plot is similar but smoother for 30x30x30, where the computation time starts to become significant on the order of seconds rather than milliseconds). The maximum DOS at just over 400 cm^-1 is in agreement with the Dispersion graph, where the line ω = ω_{maximum states} with the dispersion branches is greatest.

Free Energy within the Quasi-Harmonic Approximation

The quasi-harmonic approximation is a development of the harmonic approximation for lattice vibrations, the latter of which treats all vibrating atoms as simple harmonic oscillators. The limitation to this treatment lies in the equilibrium bond distance, which is invariable under vibrational energy. To correct for this, the quasi-harmonic model retains the harmonic motion of individual atoms, but adjusts the bond distances and hence phonon frequencies as a function of temperature to account for thermal expansion, avoiding the need to apply an anharmonic potential. A large collections of phonons are sampled on a grid matrix, and the sum is used to determine the free energy. Minimising the free energy with respond to bond distances allows the lattice parameter to be determined and updated accordingly, resulting in expansion as the free energy decreases.

The Helmholtz energy formula:

$A_{(T,V)}=U_{(V)}-T{S}_{(T,V)}$ can be expressed as: $A(T,V)=E_0+\frac{1}{2}\sum _{j,k}\overline{h}{\omega }_{j,k}+k_{B}T\sum _{j,k}\ln (1-e^{\frac{-\overline{h}{\omega }_{j,k}}{k_{B}T}})$

where E₀ is the zero-point energy, $\frac{1}{2}\sum _{j,k}\overline{h}{\omega }_{j,k}$ is the vibrational energy contribution, and $k_B\sum _{j,k}\ln (1-e^{\frac{-\overline{h}{\omega }_{j,k}}{k_{B}T}})$is the vibrational entropy contribution, ħ is the reduced Planck constant, ω_j,k is the phonon frequency, j is the sampled atom, k is the wavevector (1D space), k_B is the Boltzmann constant and T is temperature. The entropic term arises from a partition function.

The Helmholtz Free energy per primitive unit cell for MgO with increasing number of k-points sampled (grid sizes 1x1x1 to 5x5x5). Convergence is visible at the latter data point.

Given that ω is modeled using a harmonic potential where equilibrium bond distance increases as a function of temperature, ω is expected to decrease with increasing temperature due to weaker interatomic interactions and hence a smaller phonon energy bandwidth (where bandwidth is intrinsically related to bond distance). The magnitude of the logarithmic term tends to negative infinity as the exponential term tends to 0 with increasing temperature, corresponding to an increase in entropy with temperature (and hence decrease in free energy). At the lower temperature limit, the vibrational entropy tends to 0 due to occupation of the vibrational ground states, and because the entropic contribution is negligible, the gradient of the free Energy curve is low at low temperatures but increasing.

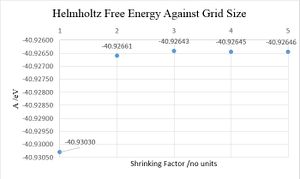
The Free energy of an infinite MgO lattice has been calculated for various grid sizes in order to numerically test the convergence of free energy with the number of phonons sampled. As a preliminary to thermal expansion studies, single point type GULP calculations were run at simulated temperatures and pressures of 0 K and 0 GPa at various grid sizes until convergence to 4 decimal places of precision was achieved. It has been shown that the free energies for grid sizes 3x3x3 and above converge to the same value to 3 decimal places (accurate to 1 meV), sizes 2x2x2 and above converge accurately to the the 0.5 meV, and sizes 5x5x5 and above converge accurately to the 0.1 meV (rounding to even). Shrinking factor 5 has been shown to be optimal for accurate free energy calculation at minimal computation time expense, and this grid size has also been used in literature computational study.

Thermal Expansion within the Quasi-Harmonic Approximation

Free energy optimisation GULP calculations were run at a simulated pressure of 0 GPa at various temperatures from 0 K to 1000 K in 100 K increments. The phonon DOS was calculated for each simulation over a 5x5x5 grid size and the lattice parameters and free energies per unit cell were hence determined at each temperature. Taking the starting volume of the crystal at 0 K, the volumetric thermal expansivity is defined as:

${\alpha }_V=\frac{1}{V_{initial}}{\left(\frac{\partial V}{\partial T}\right)}_P$

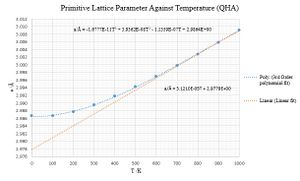
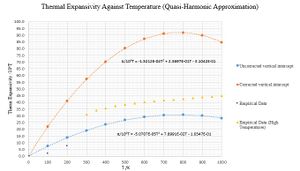
The Lattice parameter against Temperature curve has been plotted and fitted to a 3rd order polynomial and differentiated numerically (multiplying vertical axis values by 3 to convert from linear to volumetric dimensions according to ${\alpha }_V=3{\alpha }_L$. Substituting T values into the derivative allowed α_V to be plotted against temperature to obtain a temperature-dependent thermal expansivity. A linear fit was also drawn for the linear region of lattice parameter curve to obtain a general, temperature independent α_V of 31.2 10^-6 T^-1 . For the experimental α_V(T) curve, relatively close agreement with literature was found for α_V at T = 100 K (7.3 10^-6 T^-1, 14% difference from literature α_V value of 6.3 10^-6 T^-1 extrapolated from the graph ). The α_V(T) polynomial function proves to be unreliable as small changes in the a/T polynomial fit propagate into large errors (fixing the y axis intercept for a(T) makes the curve differentiate to give a very different α_V(T) distribution.

The Helmholtz Free Energy (A) as a function of Temperature for the QHA method. A is intrinsically related to lattice parameter.

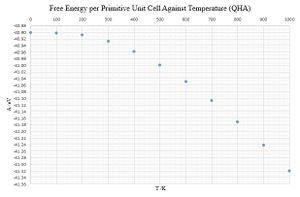
Empirically, α_V(T) displays an apparently Sigmoid curve (compared with the more parabolic QHA curve), suggesting that the potentials used in the QHA simulation were too simplistic to accurately model temperature dependence. The alternative linear fit experimental value of 31.2 10^-6 T^-1 accords exactly with the literature at 300 K (both 31.2 10^-6T^-1 ), but underestimates the expansivity at high temperatures from which the expansivity was actually calculated (28% difference). Notable features of the plotted lattice parameter and free energy curves is that the gradients of each both fall to 0 and 0 K, gradually increasing and becoming linear at 700 K and above.

Failings of the QHA model are known to arise at high temperatures due to the evolution of significant phonon-phonon and phonon-electron scattering. GULP calculations treat phonons classically and therefore don't account for the quantum particle-like behaviour of phonons, to which pseudomomenta given by ћk may be attributed. The wavevector of scattered phonon is the sum of the incident phonon wavevectors, hence momentum is conserved as long as the new k value remains in the 1st Brillouin zone. At higher temperatures however, scattering may lead to k values into the 2nd Brillouin zone, and crystal momentum is not conserved for such collisions due to the periodic nature of k. In summary, high temperatures in real materials are thought to lead to more phonon-phonon interactions that limit the expansion of the solid, accounting for the flattening of the of the empirical da/dT gradient at higher T. The QHA model ignores scattering, hence da/dT appears to increase indefinitely, achieving unrealistically high volumes and low vibrational frequencies. Phonons in real materials will also scatter against crystal defects and imperfections, which become present in significant quantities as T approaches T_m, the melting point. Close to T_m, As the QHA simulations were conducted at low pressure (0 GPA), anharmonic effects arise at very low temperatures by comparison. The failings discussed are difficult to view from the plotted graphs as generally a superlinear dα_V/dT gradient is diagnostic anharmonicity, and this cannot be shown by the somewhat inadequate polynomial α_V(T) fits. The temperature independent α_V result 31.2 10^-6 T^-1 matches the T >300 K empirical trend better than any of the other fits despite being a simple horizontal line.

The primitive lattice parameter of MgO as a function of Temperature fitted to a 3rd order polynomial (blue) and to a straight line (orange).

Molecular Dynamics Simulation

Thermal expansivities as a function of temperature determined experimentally (orange and blue lines) and empirically from literature yellow) and using similar calculation methods (purple series)^[2][3]

Raw data from MD simulation processed into primitive unit cell data by: division by 8 to obtain conventional cell volume, then division by 4 to obtain primitive unit cell volume.

T /K	V /Å3 (8 conventional cells)	V /Å3 (conventional cell)	V /Å3 (primitive unit cell)
0	n/a	n/a	n/a
15	598.1	74.76	18.69
25	598.2	74.78	18.69
50	598.6	74.83	18.71
100	599.6	74.95	18.74
200	601.2	75.15	18.79
300	602.8	75.35	18.84
400	604.3	75.54	18.88
500	606.4	75.80	18.95
600	608.2	76.03	19.01
700	610.3	76.29	19.07
800	611.0	76.38	19.09
900	613.3	76.66	19.17
1000	614.4	76.80	19.20

Physically, MD treats the lattice as a collection of independently and randomly vibrating atoms. The instantaneous interatomic forces are calculated for all atom pairs within a given range, hence the atomic accelerations are determined, hence the velocities are updated according to $v_{final}=v_{initial}+adt$ and the positions are updated similarly according to $r_{final}=r_{initial}+vdt$. For small enough timesteps dt, the system equilibrates and allows average lattice parameters to be determined for given temperatures.

Thermal expansion in MD arises due to the effect of increasing average kinetic energy on the equilibrium interatomic bond distance according to thee anharmonic contribution to the potential employed (Morse-like). It is expected that at low temperatures, the interatomic potentials would be almost harmonic and hence therefore negligible change in lattice parameter would occur as the Temperature is perturbed from 0, whilst increasing temperature will shift the time-averaged bond distance in the positive direction as a direct result of anharmonicity.

The primitive lattice volume of MgO as calculated by MD and using the QHA for the orange and blue line respectively.

An MgO crystal containing 32 unit cells (64 atoms in total) was simulated using the GULP molecular dynamics method in the isothermal-isobaric (NPT) ensemble at a pressure of 0 GPa over a range of temperatures. 500 Equilibration steps were run over a timestep of 1.0 fs, followed by 500 production steps after equilibration from which data means were extracted every 5 sampling steps. From the Volume/Temperature plot, thermal expansivity is found to be 28.3 10^-6 T^-1 and temperature independent using the MD method. This result matches the literature value at 260 K (28.2 10^-6 T^-1 ), although the results from literature show approximate temperature dependence as discussed, hence the result becomes inaccurate to 1 s.f with small perturbations in temperature of less than 10 K. The MD thermal expansivity somewhat resembles the QHA result from the linear fit, being lower with a 9.7% difference. Interestingly, the MD result fits relatively well to the the experimental QHA curve (uncorrected) above 600 K, although the QHA linear fit result remains the most accurate in this temperature domain. At low T, differences in the V(T) curves are observed as the QHA gradient starts to decrease to 0 from 400 K downwards, whilst the MD gradient appears only to change at sub 100 K temperatures (the two lines are very close in gradient and intercept above 400 K). As a result, MD predicts a higher density for MgO compared with QHA, and this trend is consistent over the sampled temperature range. At 300 K, the density predicted by MD accords more closely at 3.553 g cm^-3 cf. 3.543 cm^-3 (cf. lit. 3.576 cm^-3 ). As such, it appears that MD more accurately optimises the MgO lattice parameter and the thermal expansivity at low temperatures, whilst QHA offers the most accurate thermal expansivity value for temperatures around 300K and slightly above, perhaps illustrating the Beyond 1000 K, the expected failure of QHA would imply MD to be more suitable for determining expansion, as MD is capable of modeling phase transitions such as melting (where liquids are generally more expandable under temperature than solids), unlike QHA.

Conclusion

Within the 0 K to 1000 K temperature range, the QHA method offers a more accurate thermal expansivity value for 300 K > T > 1000 K, whereas the MD value is accurate to 2 s.f. at 260 K with accuracy to the nearest 5x10^-6 T^-1 in an approximate 100 K range. The more accurate density prediction of MD suggests that the anharmonic potential offers greater accuracy when optimising volume compared with the QHA harmonic potentials. Deviations between the calculated and literature α_V values have been attributed to the limitations of the potential surfaces used to model both the phonons and the anharmonic MD potential; many more such potentials are available for use with GULP and investigations into quantum potentials could be used to modify the somewhat successful QHA method in attempt to improve the α_V(T) fit by accounting for previously neglected phonon-phonon and phonon-electron scattering. Doing so might aid in determining exactly where the QHA method becomes inappropriate for use so that corrections to the method may be made, given the documented unreliability of the QHA at 0 GPa pressures. Calulations at greater pressures would also be needed to model real-life systems, which are not subject to the 'ideal' 0 pressure as has been approximated, which could potentially cause a significant discrepancy between calculated and literature values.