Rep:Mod:CPh

Module 3 (physical) of the Year 3 Computational Modelling Labs by Jan Szopinski. Please do not edit this page.

The Cope Rearrangement Tutorial

Optimizing the reactants and products

Within each of the gauche, app etc, various energy minima are possible. The experimental script contains an extensive list. Not all of them were recalculated but selected ones are presented in Table 1. The conformers will be referred to with their identifyiers from the experimental script for the sake of consistence. The energy minima were confrmed by the absence of imaginary frequencies.

Fig. A relaxed scan of central dihedral angle at HF/3-21G level of theory.

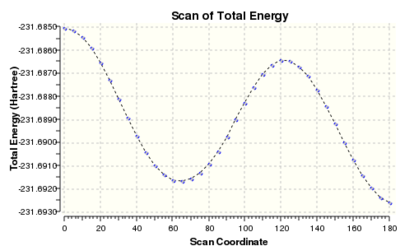
Scan

The scan profile of the central dihedral (C2-C3-C4-C5) of a butane molecule is well-known. Staggered conformations are energy minima, while eclipsed conformations can be regarded as transition states between them. It is also known that antiperiplanar structure is slightly (0.9 kcal/mol) lower in energy than gauche conformations. To find the influence of unsaturation on the both ends of hexadiene molecule, a relaxed scan of the dihedral angle around the central C-C bond was performed. The starting structure had an s-cis conformation with carbon atoms contained in one plane. The calculation was conducted at HF/3-21G and consisted of 36 steps of 5 degrees, encompassing a half of the full angle, which is sufficient due to the symmetry of the molecule. The scan profile is shown on the right. The minimum just above 60 degrees corresponds to a gauche conformation and the minimum at 180 corresponds to antiperiplanar conformation. The calculation suggests that the gauche conformation is higher in energy than the app by 0.60 kcal/mol.

Anti

Two app minima were found. The first one was found in an optimization performed on the structure used in the scan but cleaned by GV. The optimized structure and energy corresponded to the anti1 entry in the experimental script. To find another minimum of the app conformation, the C1-C2-C3-C4 dihedral angle in the cleaned structure was changed from 150 to -150 degrees. This optimization yielded a different local minimum. Their energies are included in the table. The energy difference was...

Gauche

Similarly, to give a more varied and representative view of the structures, two minima were found. The initial structure was first one was found by changing the central dihedral from 180 to 60. Optimizing such structure yielded gauche2, and cleaning before optimization gauche4. The lowest energy conformer, as per experimental script, gauche3 was not found. To locate it, the gauche 2 from ca -123 to 150 degrees. The global minimum was then successful reached in the optimization.

Summary of structures

Conformer	Structure	Point Group	Energy/Hartrees HF/3-21G	Relative Energy in kcal/mol	Energy/Hartrees B3LYP/6-31G*	Relative Energy in kcal/mol
		C2	-231.69260	0.04	-234.61180	0.00
		Ci	-231.69254	0.08	-234.61171	0.06
		C2	-231.69167	0.62	-234.61069	0.70
		C1	-231.69266	0.00	-234.61133	0.30
		C2	-231.69153	0.71	-234.61048	0.83

Fig. Infrared spectrum of liquid 1,5-hexadiene film from the SDBS overlaid with calculations at B3LYP/6-31G* with scaling factor of 0.9613

Fig. Infrared spectrum of liquid 1,5-hexadiene film from the SDBS overlaid with anharmonic frequency calculations at B3LYP/6-31G*.

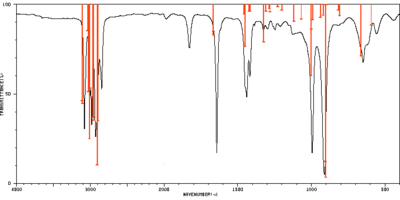
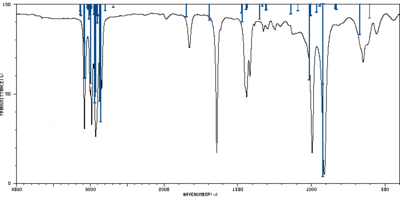
Frequency analysis and thermochemistry of gauche3 conformer

The frequency calculation was performed at B3LYP/6-31G* level of theory. The relevant scaling factors are 0.9613 for frequencies and 0.9804 for thermochemical values. A frequency calculation with anharmonic corrections was also conducted at the same level of theory. The table below shows all calculated frequencies with assigned vibrations. The assignment was based on visual assessment of the animation in GaussView 5, however a more accurate and formal assignment could be conducted using the Total Energy Distribution method. The experimental spectrum from Spectral Database of Organic Compounds was compared with both theoretical spectra in the table below. All theoretical intensities were normalized to the peak of maximum intensity treated as 100%.

Experimental		B3LYP/6-31G*
SDBS		Harmonic (scaled by 0.9613)			Anharmonic
Wavenumber / cm-1	100% - T / %	Wavenumber / cm-1	Intensity (normalized)	Assignment	Wavenumber / cm-1	Intensity (normalized)	Assignment
557	21	594	12	C=CH2 twisting	606	8	←
649	34	663	30		673	18	←
		809	7	C=CH2 and CH2 rocking
913	96	903	100	C=CH2 wagging	922	46	←
		904	91		923	100	←
		919	6	C=CH2 and CH2 rocking
		939	8
					966	5	C=CH2 rocking and C=CH bending
994	84	991	9	C=CH2 twisting and CH2 wagging	1005	7	C=CH torsion
		1001	14	C=CH torsion	1008	7	C=CH2 twisting and CH2 wagging
		1003	41		1015	44	←
		1069	8	C=CH torsion+bending and CH2 twisting	1092	4	←
		1119	10	C=CH bending and C=CH2 rocking	1140	6	←
1207	16
1213	16
1247	19
1257	16
1298	16	1281	4	C=CH bending and C=CH2 scissoring	1310	4	C=CH bend
		1308	4	CH2 twisting
1327	19	1324	22	CH2 wagging	1352	9	CH2 wagging
1384	16
1418	43	1416	4	C=CH2 scissoring	1469	10	CH2 scissoring
		1422	4
1440	54	1451	24	CH2 scissoring	1475	5	←
		1457	6
1643	84	1665	18	C=C stretch	1692	10	←
		1666	16
1828	28				1849	7	C=CH2 wagging overtone
					1851	7
					2799	4	CH2 scissoring overtone
2847	50	2895	67	C-H2 symmetric stretch	2860	68	←
		2906	93		2872	56	C-H2 symmetric stretch
					2902	7	Combination band of 1475 and CH2 scissoring
					2907	11
					2911	6	Combination band of 1475 and C=CH2 scissoring
					2914	5
2928	74	2954	67	C-H2 antisymmetric stretch	2930	51	←
		2963	65		2936	53	C-H2 antisymmetric stretch
					2942	57	C=C-H stretch
					2952	6	Combination of CH2 scissoring 1469 and 1475
2981	69	3010	78	C=C-H stretch	2994	46	C=C-H2 symmetric and C=C-H stretch
3001	53	3028	50	C=C-H2 symmetric and C=C-H stretch	3005	6
		3035	15		3017	8
		3037	15
3081	71	3107	57	C=C-H2 antisymmetric stretch	3082	23	C=C-H2 antisymmetric stretch
		3110	56		3083	43
					3086	21	CH2 scissoring overtone
					3133	7	Combination of C=CH2 scissoring and C=C stretch
					3136	5	Combination of 1692 and C=CH2 scissoring
					3138	4	Combination of C=CH2 scissoring and C=C stretch

Selected peaks of normalized intensities above 4% were assigned to their experimental counterparts to compare the harmonic and anharmonic calculations. Standard deviation for both methods in two frequency regions were calculated and the results are summarized in the table below. While the assignment was to some degree arbitrary, it is clear that harmonic frequencies are better than anharmonic for low wavenumbers and the situation is opposite for the high wavenumber region. This agrees with the fact that high frequency vibrations contain a high degree of anharmonictiy, which has to be accounted for.

Experimental	Harmonic		Anharmonic
Wavenumber / cm-1	Wavenumber / cm-1	Difference squared / cm-2	Wavenumber / cm-1	Difference squared / cm-2
557	594	1380	606	2392
649	663	192	673	585
913	905	63	923	97
994	1001	46	1013	376
1298	1294	16	1310	135
1327	1324	9	1352	638
1418	1419	1	1469	2648
1440	1452	142	1475	1199
1643	1665	499	1692	2391
Standard deviation of low wavenumbers		16 cm-1		34 cm-1
2847	2902	2975	2866	344
2928	2958	921	2937	75
2981	3010	870	2994	171
3001	3031	892	3012	115
3081	3108	746	3083	5
Standard deviation of high wavenumbers		36 cm-1		12 cm-1
Overall standard deviation		25 cm-1		28 cm-1

Optimizing the transition structures

The chair transition state structure has been found by requesting optimization from a sensible guess structure, which was obtained by optimizing with frozen reaction coordinate. The transition state was confirmed by one imaginary frequency obtained in frequency vibration at the same level of theory. An IRC calculation proved that the reaction leads to a gauche2 conformation.

A boat transition structure was obtained from the QST2 algorithm implemented in Gaussian. An imaginary frequency confirmed that it was the structure sought for. An IRC calculation showed that the reaction leads to a conformer, which itself is a transition structure with respect to central dihedral bond torsion.

The Diels Alder Cycloaddition

Reaction of Butadiene with Ethene

Molecular orbital analysis of reactants

The Highest Occupied and Lowest Unoccupied Molecular orbitals of ethene and butadiene are shown in the table below. The symmetry of orbitals with respect to the central plane can be easily seen from the figures. HOMO of ethene and LUMO of butadiene are symmetric, while LUMO of butadiene and HOMO of ethene are antisymmetric. This match allows them to interact in a cycloaddition reaction.

	HOMO	LUMO
ethene
butadiene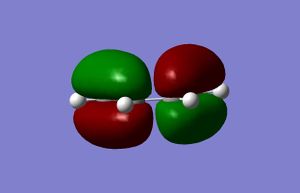

Energies and location of transition state

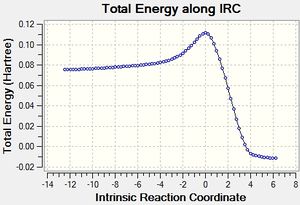
A guess for the structure of transition was made by making slight changes to the reactants and arranging them in a sensible manner. An optimization to transition state was requested using the AM1 semi-empirical method and a frequency calculation at the same level of theory showed one imaginary frequency, which is presented on the central figure and agrees with the expected vibration. An IRC calculation in both direction confirms that the transition state is between reactants (figure on the left) and the cycloaddition product (right). A plot of the IRC calculation allows to estimate the reaction energy barrier. A more accurate result can be obtained from energy values in the table below.
The bond length of the both sigma bonds being formed in the transition structure was calculated to be 2.119 Å. As this bond length was almost identical in the transition state, it can be concluded that this step was synchronous, which agrees with the simultaneous displacements in the imaginary frequency visualisation. At the same time, the central butadiene bond has shortened from 1.449 Å to 1.397 Å.

The lowest real frequency (147 cm^-1) corresponds to a rotation of the molecules with respect to each other. As a real vibration is expected to, it does not seem to lead to any bond breaking.

Molecular orbitals of transition state

The HOMO and LUMO of the transition state structure are shown on Figures X and Y respectively. It can be seen from the figures, that the HOMO is antisymmetric and LUMO antisymmetric with respect to the central plane. The symmetry considerations allow to conclude the following mixing relations:

antisymmetric: HOMO_TS = HOMO_butadiene + LUMO_ethene
symmetric: LUMO_TS = LUMO_butadiene + HOMO_ethene

Orbital

Orbital

Reaction of 1,3-cyclohexadiene with maleic anhydride

Molecular orbital analysis of reactants

The symmetry with respect to the central plane has been noted in the table below. Similarly to the reaction of butadiene and ethene, this reaction is allowed as there is a symmetry match between the HOMO of maleic anhydride with LUMO of 1,3-cyclohexadiene, as well as a match between HOMO of the latter with the LUMO of the former.

	HOMO	LUMO
maleic anhydride	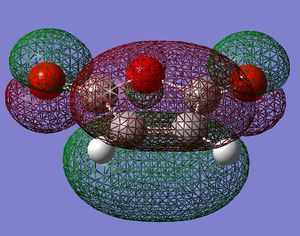symmetric	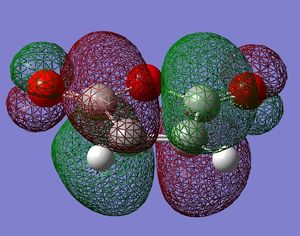antisymmetric
1,3-cyclohexadiene	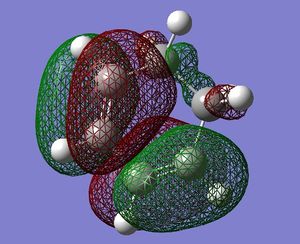antisymmetric	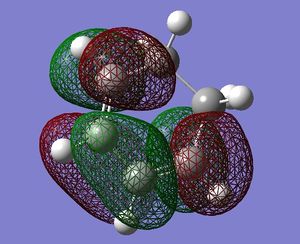symmetric

Energies and location of transition state

The table below summarizes the energies of reactant, product and transition state molecules. To obtain a higher level of accuracy, a B3LYP/6-31G* level of theory was employed for stationary point structures. The results show that the endo form is lower in energy by about 1.6 kcal/mol.

caption

Molecule	Energy (AM1) / Hartree	Energy (B3LYP/6-31G*) / Hartree
Maleic anhydride	-0.12182	-379.28954
1,3-cyclohexadiene	0.02771	-233.41894
endo TS	-0.05151	-612.68340
endo product	-0.16017	-612.75829
exo TS	-0.05042	-612.67931
exo product	-0.15991	-612.75579

Molecular orbitals of transition state

The interactive figures in the table present the HOMO and LUMO orbitals of the endo and exo transition states. All orbitals were antisymmetric with respect to the central plane

approach	HOMO	LUMO
endo	Orbital	Orbital
exo	Orbital	Orbital

Abbreviations

app = antiperiplanar
TS = transition state