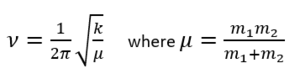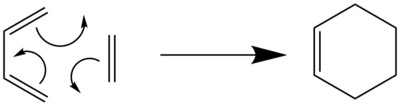Rep:Mod:CPYX TS
Introduction
Transition states
A transition state is a maximum point on the minimum energy path on a potential energy surface. This means that it is at a relative minimum along 1 direction and at a relative maximum along the crossing direction. This point is known as a saddle point, as it is neither a minimum nor a maximum. A minimum has the lowest energy in its local area on a potential energy surface. At a minimum, the gradient is negative before that point and positive after that point.
The gradient of the potential energy surface is 0 at both a minimum and a transition state. The second partial derivatives along the reaction coordinate can be used to differentiate between these points. The second partial derivative of a minimum point always has a positive value, whereas the second partial derivative of a transition state along the reaction coordinate has a negative value.
The second partial derivatives give the force constants k. The frequency ν can then be calculated using the formula
Thus, all frequencies calculated for a minimum are real and positive. A frequency calculation for a transition state will result in 1 imaginary frequency as the force constant, k, used to calculate it is negative. In Gaussview, this frequency is reported as a negative number. The vibrational mode associated with this frequency corresponds to the reaction path and the energy can be lowered by distorting the geometry along this mode in the direction of the reactants or the products.
The study of transition structures is very useful in predicting the reactivity of a reaction where more than one set of products may be formed. Often, the set of products formed are the most thermodynamically stable products for the reaction, which are also known as thermodynamic products. However, there are several cases where the thermodynamically less stable products predominate, and this may be due to stabilising interactions in the transition state leading to this set of products, lowering the activation energy. These products are known as kinetic products as they are formed faster due to a lower energy barrier that needs to be crossed to form these products as compared to other sets of products.
Nf710 (talk) 22:35, 8 February 2018 (UTC) You need to say this is in 3N-6 Degrees of freedom. And you get the frce constant by diagonalising the hessian.
The Diels-Alder reaction
The Diels-Alder cycloaddition reaction is a common type of reaction where kinetic products are known to predominate. In this reaction, often known as a [4+2] cycloaddition, a diene reacts with a dienophile, normally an alkene, in a concerted mechanism to form a 6-membered ring. Normally, the diene is electron-rich while the dienophile is electron-poor, and the main orbitals interacting during the reaction are the HOMO of the diene and the LUMO of the dienophile. However, there are some exceptions, including hetero-Diels-Alder reactions, where there is inverse electron demand and the diene is more electron-poor than the dienophile. In this case, the main orbitals interacting during the reaction are the HOMO of the dienophile and the LUMO of the diene. The Diels-Alder reaction between butadiene and ethylene, which will be investigated in Exercise 1, is shown below. This is a conventional Diels-Alder reaction.
Where there are selectivity issues in a Diels-Alder reaction, the kinetic endo product is preferred in irreversible reactions over the thermodynamic exo product. This is due to the stabilization of the endo transition state by orbital, dipolar and Van der Waals interactions between the atoms on the dienophile which are not involved in the formation of the 6-membered ring and the back of the diene. These stabilizing interactions are absent in the exo transition state, as these atoms on the dienophile and the back of the diene are too far away to interact.
In this lab course, 3 different Diels-Alder reactions were investigated. The first reaction involves a simple formation of cyclohexene from butadiene and ethylene. There are no selectivity issues in this reaction, which was investigated to introduce the Diels-Alder reaction and show the molecular orbitals (MOs) that normally interact in Diels-Alder reactions. The subsequent Diels-Alder reactions are more complicated and involve the formation of endo and exo adducts. The reaction barriers and reaction energies for the formation of endo and exo adducts are calculated and secondary orbital interactions are discussed. For the 3rd reaction involving xylylene and sulphur dioxide, another type of reaction, known as a cheletropic reaction, can take place. This will be explained later on.
Methods for optimisation and data collection
Gaussview software was used to analyse transition structures, visualize MOs of these structures and predict the reactivity of the reactions studied. 2 different electronic methods were used to optimise the structures of reactants, products and transition states. They are the semi-empirical PM6 method and the Density Functional Theory (DFT) B3LYP method. PM6 is a faster method as it uses experimental data to save time and resources. Where structures were optimised using the slower but more accurate B3LYP method, PM6 was used to generate initial geometries, which were then optimised with B3LYP.
The energies of optimised structures at room temperature were obtained from the "Themochemistry" section in their log files after a frequency calculation, and the values used are the "Sum of electronic and thermal Free Energies". These values were then used to calculate the activation and reaction energies reported below for Excercises 2 and 3.
Nf710 (talk) 22:37, 8 February 2018 (UTC) You could have gone into more setail about the computational methods by showing some equations etc.
Exercise 1: Reaction of butadiene and ethylene
Molecular orbitals
The reactants cis-butadiene and ethylene, the product cyclohexene and the transition state structure for the Diels-Alder reaction were optimised using the PM6 method. The 2 tables below show the Jmol files of the HOMO and LUMO of cis-butadiene and ethylene and the 4 MOs they produce in the transition state (TS) for this Diels-Alder reaction, which are MO 16, MO 17, MO 18 and MO 19. Even though trans-butadiene is the more stable conformation of butadiene, the cis-butadiene conformation was used as it is the conformation that reacts in the Diels-Alder reaction. The transition state was confirmed using an intrinsic reaction coordinate (IRC) and the links to the log file of the IRC and the product of this reaction, cyclohexene, are shown below the tables.
| Butadiene HOMO | Butadiene LUMO | Ethylene HOMO | Ethylene LUMO | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MO 16 | MO 17 | MO 18 | MO 19 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Transition state IRC: File:CPYX EXERCISE 1 IRC.LOG
Cyclohexene: File:EXERCISE 1 MINIMUM 1.LOG
(Fv611 (talk) Your MO diagram is nice and constructed correctly, but you haven't found the true minimum structure for the butadiene, leading to relative FMO energies that are slightly off.)
Using these orbitals, as well as the relative energies of these orbitals, a MO diagram for the formation of the TS from butadiene and ethylene was constructed. The MO diagram is shown below, where s stands for symmetric orbitals and a stands for antisymmetric orbitals.
From the diagram above, symmetric orbitals combine with symmetric orbitals to form symmetric orbitals, while antisymmetric orbitals combine with antisymmetric orbitals to form antisymmetric orbitals. Antisymmetric orbitals are not able to combine with symmetric orbitals, even if they are close in energy. This means that the orbital overlap integral is zero for the case of a symmetric-antisymmetric interaction and it is non-zero for symmetric-symmetric interactions and antisymmetric-antisymmetric interactions.
Changes in bond lengths
The changes in bond lengths during the Diels-Alder reaction are shown below.
| Bond type in reactants | Bond length in reactants (Å) | Bond type in cyclohexene | Bond length in transition state (Å) | Bond length in cyclohexene (Å) | Change in bond length |
|---|---|---|---|---|---|
| C=C bond in ethylene | 1.32741 | C-C bond | 1.38176 | 1.56032 | Increase |
| C=C bonds in butadiene | 1.33482 | C-C bond | 1.37979 and 1.37974 | 1.49118 | Increase |
| C-C bond in butadiene | 1.46892 | C=C bond | 1.41111 | 1.36311 | Decrease |
| None (shown as dotted lines in TS MOs above) | N/A | C-C bond | 2.11439 and 2.11508 | 1.58339 | Decrease |
The typical sp3 and sp2 C-C bond lengths are 1.54 Å and 1.34 Å respectively and the Van der Waals radius of the C atom is 1.70 Å. From the table above, the lengths of the partly formed C-C bonds in the transition state are larger than the typical sp3 bond length but they are much shorter than 2 times the Van der Waals radius of the C atom. The other bond lengths in the transition state are in between the sp3 and sp2 C-C bond lengths. In the cyclohexene product, the newly-formed C-C bonds have bond lengths of 1.58 Å, which are typical of sp3 carbon atoms.
Reaction coordinate
The vibration corresponding to the reaction coordinate is shown below.
From the picture above, the formation of the 2 bonds is synchronous as these 2 bonds are formed simultaneously, in that these 2 bonds have almost the same lengths as each other throughout the reaction.
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole
Molecular orbitals
(Fv611 (talk) Your MO diagram is good, but you do not discuss at all the difference between the exo and endo transition state from the perspective of the relative MO energies.)
The reactants cyclohexadiene and 1,3-dioxole, the endo and exo TSs and adducts were optimised using the B3LYP/6-31G(d) method. The Jmol files of the reactants and the 2 different products that can be generated in this reaction are shown in the table below.
| Cyclohexadiene | 1,3-Dioxole | Exo adduct | Endo adduct | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
The MO diagram for the formation of both the exo and endo TS was constructed and it is shown below. The ordering of the energy levels is the same for both the endo and the exo TS. Only the p orbitals are shown in the orbital representations. The p orbitals of the oxygen atoms are shaded a lighter colour as they do not form primary orbital interactions in the TSs. MOs 40 and 41 are the bonding combinations while MOs 42 and 43 are the antibonding combinations.
From the diagram above, the HOMO of the dienophile, 1,3-dioxole, is higher in energy than the HOMO of cyclohexadiene. This means that the HOMO of the dienophile and the LUMO of the diene are closer in energy than the HOMO of the diene and the LUMO of the dienophile, making the HOMO of the dienophile and the LUMO of the diene the main orbitals involved in the Diels-Alder reaction. Hence, this reaction is an inverse electron-demand Diels-Alder reaction, unlike a normal Diels-Alder reaction where the main interacting orbitals are the HOMO of the electron-rich diene and the LUMO of the electron-poor dienophile.
Nf710 (talk) 22:48, 8 February 2018 (UTC) How do you know this?
The Jmol files of the HOMO and LUMO of the reactants as well as the MOs 40, 41, 42 and 43 for each of the exo and endo TSs are shown in the 3 tables below. For the endo TS, MO 41 is displayed with an isovalue of 0.01 to observe secondary orbital interactions.
| Cyclohexadiene HOMO | Cyclohexadiene LUMO | 1,3-dioxole HOMO | 1,3-dioxole LUMO | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Exo TS | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MO number | MO 40 | MO 41 | MO 42 | MO 43 | ||||||||
| Jmol files | ||||||||||||
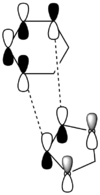
| Symmetric/ antisymmetric | Antisymmetric | Symmetric | Symmetric | Antisymmetric | ||||||||
| Chemdraw representations of MOs | 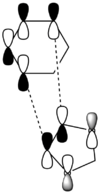 |
 |
 |
| ||||||||
| Endo TS | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MO number | MO 40 | MO 41 | MO 42 | MO 43 | ||||||||
| Jmol files | ||||||||||||
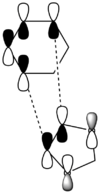
| Symmetric/ antisymmetric | Antisymmetric | Symmetric | Symmetric | Antisymmetric | ||||||||
| Chemdraw representations of MOs |  |
 |
 |

| ||||||||
For the endo TS, there is a bonding interaction between the p orbitals at the back of cyclohexadiene and the p orbitals on both oxygen atoms on 1,3-dioxole in MO 41, the HOMO. This stabilizing secondary orbital interaction is not present in the exo TS, making the endo TS have a lower energy than the exo TS.
Activation and reaction energies
The energies of the optimised structures are recorded below.
| Structure | Energy at room temperature (Hartrees) |
|---|---|
| Cyclohexadiene | -233.324375 |
| 1,3-Dioxole | -267.068643 |
| Exo TS | -500.329164 |
| Exo product | -500.417320 |
| Endo TS | -500.332147 |
| Endo product | -500.418692 |
These energy values recorded above were used to calculate the activation and reaction energies for each of the 2 different products formed, using the formulas below.
Activation energy = Energy of TS - combined energies of reactants
Reaction energy = Energy of product - combined energies of reactants
A negative reaction energy means that the product is more stable than the reactants and energy is given off when the product is formed. The energy values in kJ/mol are rounded off to 3 significant figures.
| Product formed | Activation energy (Hartrees) | Activation energy (kJ/mol) | Reaction energy (Hartrees) | Reaction energy (kJ/mol) |
|---|---|---|---|---|
| Exo product | 0.063854 | 168 | -0.024302 | -63.8 |
| Endo product | 0.060871 | 160 | -0.025674 | -67.4 |
As the activation energy needed to form the endo product is lower than the activation energy needed to form the exo product, the endo product forms more easily and quickly. Thus, the endo product is kinetically favourable.
As the endo product has a lower energy and is more stable than the exo product, and the reaction energy for the formation of the endo product has the more negative value, it is the thermodynamically favourable product.
Nf710 (talk) 22:53, 8 February 2018 (UTC) Your enegies are corect and you have come to the correct conclusion however you explanations were quite brief and you could have gone into more detail.
Exercise 3: Reactions of Xylylene and SO2 - Diels-Alder vs Cheletropic
Introduction
The reactants xylylene and SO2, the endo and exo Diels-Alder and cheletropic TSs and products were optimised using the PM6 method. The optimised structures of xylylene, the diene, and SO2, the dienophile, are shown below.
| Xylylene | SO2 | ||||
|---|---|---|---|---|---|
This reaction, unlike the previous 2 reactions investigated, is not purely a Diels-Alder reaction. There is another competing reaction known as a cheletropic reaction. A cheletropic reaction is similar to a Diels-Alder reaction in that it is a pericyclic cycloaddition reaction. The key distinguishing feature of cheletropic reactions is that both new bonds are made to the same atom on one of the reactants. [1] Cheletropic reactions involving SO2 are commonly observed.
The reaction coordinates for these different reactions, as well as the links to the log files of the transition states and products are shown in the table below.
| Exo Diels-Alder reaction | 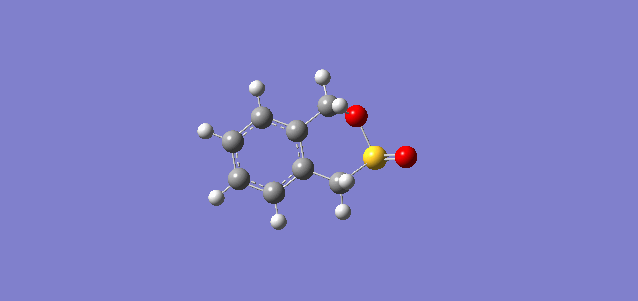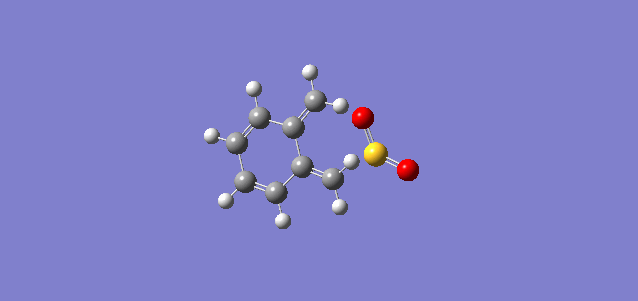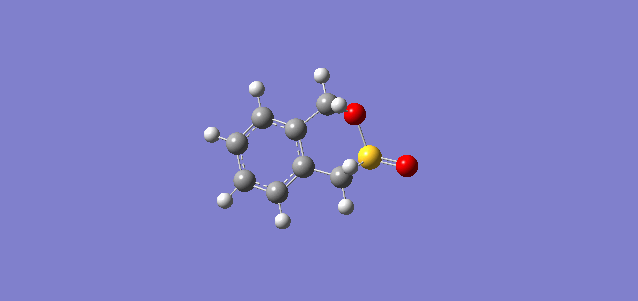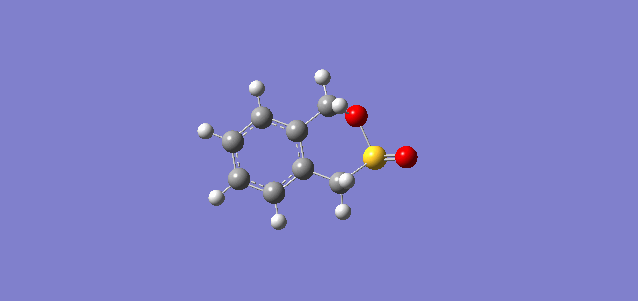 |
File:CPYX Exercise 3 exo-TS.LOG |
| Endo Diels-Alder reaction |  |
File:CPYX Exercise 3 endo TS.LOG |
| Cheletropic reaction |  |
File:CPYX Exercise 3 cheletropic TS.LOG |
Activation and reaction energies
The energies of the optimised structures are recorded below.
| Structure | Energy at room temperature (Hartrees) |
|---|---|
| Xylylene | 0.178031 |
| SO2 | -0.118614 |
| Exo Diels-Alder TS | 0.092078 |
| Exo Diels-Alder product | 0.021452 |
| Endo Diels-Alder TS | 0.090558 |
| Endo Diels-Alder product | 0.021704 |
| Cheletropic TS | 0.099062 |
| Cheletropic product | 0.000005 |
Using these energies recorded above, the activation and reaction energies for the formation of the 3 different products were calculated as in the previous exercise and they are shown below, in units of Hartrees and converted to kJ/mol.
| Product formed | Activation energy (Hartrees) | Activation energy (kJ/mol) | Reaction energy (Hartrees) | Reaction energy (kJ/mol) |
|---|---|---|---|---|
| Exo Diels-Alder product | 0.032661 | 85.8 | -0.037965 | -99.7 |
| Endo Diels-Alder product | 0.031141 | 81.8 | -0.037713 | -99.0 |
| Cheletropic product | 0.039645 | 104 | -0.059412 | -156 |
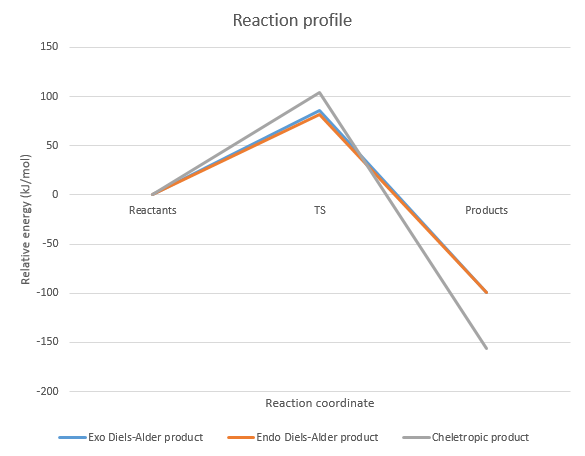
These activation and reaction energies were used to create a reaction profile for each of the 3 reactions. The reaction profiles are shown below, where the 0 kJ/mol energy level is set to the reactants at infinite separation.
From this reaction profile, the thermodynamically favoured product is the cheletropic product, as it has the lowest energy. However, the activation energy required to form this product is the highest among the 3 different reactions. Thus, the cheletropic product is only likely to be the major product when a lot of energy is pumped into the system and the conditions are equilibrating.
The energies of the endo and exo Diels-Alder transition states and products are relatively similar. The kinetically favoured product is the endo Diels-Alder product as the activation energy required to form this product is the lowest. Similar to the endo product in Exercise 2, this is also likely due to a bonding interaction between the p orbital of the oxygen atom on SO2 that is not involved in ring formation and the conjugated π system on the back of xylylene. However, the endo Diels-Alder product has a higher energy and is less stable than the exo Diels-Alder product. Thus, the endo Diels-Alder product is likely to be the major product when non-equilibrating conditions and low temperatures are used, and the reaction between the reactants is irreversible.
Driving force for all 3 reactions
The main driving force for all the 3 reactions is the formation of a stable aromatic benzene ring from non-aromatic reactants, as seen in the gif files of the reaction coordinates above. Although the diene reactant, xylylene, is planar and has a conjugated π system containing 8 π electrons, they are not arranged in a ring. Even if they were arranged in a ring, it will contain (4n) π electrons, so it will be anti-aromatic and highly unstable. This means that xylylene is highly unstable and will want to attain aromaticity, making it a very good diene for cycloaddition reactions.
Xylylene prefers to react using its outer cis-butadiene fragment. There is also another cis-butadiene fragment within the 6-membered ring, but reaction at this site is disfavoured due to steric hindrance and the formation of a slightly strained bicyclic ring system. This is shown in the figure below. The bicyclic products formed do not benefit from aromatic stabilization or increased conjugation, unlike the products formed when the outer cis-butadiene fragment of xylylene reacts which benefit from aromatic stabilization. In fact, the degree of conjugation is lowered in the bicyclic products, as their conjugated π system contains only 4 π electrons.
This is proven using the energies of the endo and exo Diels-Alder transition states and products after optimization at the PM6 level that will hypothetically form if xylylene reacts at this site. These energies are shown in Hartrees in the table below, with the links to the log files where these energies are taken from.
| Endo transition state | Endo product | Exo transition state | Exo product |
|---|---|---|---|
| 0.102069 | 0.065610 | 0.105054 | 0.067305 |
| File:CPYX EXTENSION ENDO TS.LOG | File:CPYX EXTENSION ENDO PRODUCT.LOG | File:CPYX EXTENSION EXO TS.LOG | File:CPYX EXTENSION EXO PRODUCT.LOG |
From this data, the endo transition state and product are more stable. However, they are still much higher in energy than the energies of both the endo and exo Diels-Alder transition states and products formed when xylylene reacts using its outer cis-butadiene fragment. A higher activation energy barrier has to be crossed for reaction to take place using the cis-butadiene fragment within the ring. The high instability of both possible products formed as compared to the previous 3 products investigated also adds to this difficulty. Thus, both the endo and exo Diels-Alder reactions using the cis-butadiene fragment within the ring in xylylene are very thermodynamically and kinetically unfavourable.
(Well written section Tam10 (talk) 13:25, 4 February 2018 (UTC))
Conclusion
3 different Diels-Alder reactions were investigated in this lab course to investigate the role of transition states in the reactivity of these reactions. The main pairs of molecular orbitals that would interact with each other in these reactions were found to be the HOMO of the diene and the LUMO of the dienophile, as well as the LUMO of the diene and the HOMO of the dienophile. This is due to the symmetries of these molecular orbitals, as only orbitals of the same symmetry can react with each other. The reaction between cyclohexadiene and 1,3-dioxole was found to be an inverse electron-demand Diels-Alder reaction as the LUMO of cyclohexadiene and the HOMO of 1,3-dioxole were found to be the main pair of orbitals interacting with each other in the reaction. For the same reaction, the endo TS was found to be stabilised by secondary orbital interactions between the p orbitals on the oxygen atoms on 1,3-dioxole and the p orbitals at the back of cyclohexadiene. This explains the experimental observation of endo adducts generally being the major products formed in Diels-Alder reactions, even though exo adducts may be the more thermodynamically stable products. This is the case in the reaction between xylylene and sulphur dioxide, where there is another competing reaction known as a cheletropic reaction. For this set of reactants, all 3 possible reactions are driven by the formation of a stable aromatic ring in all 3 products from non-aromatic reactants. Different reaction conditions are likely to favour different products, as the cheletropic product is thermodynamically favoured whereas the endo Diels-Alder product is kinetically favoured.
As so much information on MOs and energies that supports experimental observations can be obtained through the optimisation of transition state structures using computational methods, the computational study of transition states is indeed important in understanding the reactivity of reactions, especially where issues of selectivity are involved.
- ↑ Ian Fleming. Frontier Orbitals and Organic Chemistry Reactions. Wiley, 1976.