Rep:Mod:CMC314

Thermal expansion of MgO CID 00931629 (24/04/2017)

Introduction

Investigation of thermal expansion

It is very important to understand the thermal expansion of materials and should be investigated before using the material to build infrastructures or other application. As it results in a change in shape and volume with temperature changes, so it is crucial to predict these changes in order to find out the most suitable material for its application. For example, an expansion joint can be included in a bridge to prevent damage if the bridge located at a place where the temperature contrast is significant between day and night, shown in Figure 1.

The origin of thermal expansion arose from anharmonic interaction between molecules in the system, which lead to an increase in equilibrium spacing of the atomic bonds. As the temperature increase, more kinetic energy which motion of the molecules and they move away from their equilibrium bond length. Increase of the interspacing because the repulsion in the bond shortening is faster than the corresponding attraction after bond elongation

Qusai-harmonic (QA) approximation and molecular dynamics (MD can be used the investigate the thermal expansion and predict physical parameter such as free energy of a lattice. In both models, a lattice was assumed to be infinitely large without defect. Firstly, the size of the lattice input is optimised so that the calculation is minimised but also able to give a good estimation of the infinite crystal. QA approximation uses quantum mechanics model which the anharmonicity is neglected; On the other hand, MD uses ergodic hypothesis which states that if the sample of an ensemble is large enough, the time average is equal to the statistical average. During the calculation in molecular, the force of atoms is computed in each time step by using classical Newtonian mechanics in real time and updates the velocities and positions of the particles for the next calculation. Free movement of atoms in the model is allowed and they accelerate under the Newton's second law (F=ma) and followed by changed in velocity and position for the next step. The last averaged value can be taken to calculate the thermal expansion coefficient of the MgO. More details about both models will be discussed below.

Computational methods

In the investigation, DLVisualise v.2.4.1 was run Linux for the numerical simulation. General Utility Lattice Programme (GULP) in DLVisualise v.2.4.1 converted an interface to a molecular modelling code. GULP runs classical simulation. By running calculation GULP, physical data of the model will be able retrieved within a short computational time with high accuracy, which will be very useful for further investigation of the lattice model. OrginPro 2016 was used to proceed all the data obtained from the GULP. ionic.lib was selected for potential model and shell was not included throughout the whole simuation.

Results and Discussion

Structure and internal energy of a MgO lattice

Figure 2. A conventional cell and primitive cell of MgO

MgO is a face-centred cubic lattice (FCC) (Figure 2), )and can be described by either conventional cell or primitive cell. In the former unit cell, it is formed of four MgO cubic cells with internal angle α_c = β_c = γ_c = 90^•. In the later form, it is formed of one rhombohedron cell with internal angle α_c = β_c = γ_c = 60^• and lattice parameter a_c = b_c = c_c = 2.9783 ‎Å and cell volume = 18.6804 ų.

MgO has lattice energy of -41.0753 eV, which is the energy required to separate the Mg-O ion infinitely. Compare to literature value (-40.06 eV) , the experimental value is slight lower.

Vibration of Phonon in MgO Lattice

Density of state defined as the number of states per unit energy at given energy E. Mathematically, it is a function of E(k), where is the energy of a given wave vector k. From Figure 3, the phonon dispersion graph illustrates the vibration frequencies of the vibrational modes. There are six branches as there are two ions of Mg²⁺ and O^2- vibrate in three-dimension, which results into six vibrational modes.

Figure 3. Phonon dispersion curve of MgO

The 1x1x1 Phonon DOS graph in the first row of Figure 4, there are four available energy levels for phonon population, shown by four frequencies at 288.49, 351.76, 676.23 and 818.82 cm^-1, with relative intensity 2:2:1:1. By matching these frequencies to the dispersion relation curve in Figure 3, they all hit the k-point at L, suggested L is that single k-point in the grid. In addition, the estimation was further proved from the Log output of the 1x1x1 grid calculation, and it has a coordination of (0.5, 0.5, 0.5). the relative intensity of the peaks suggests the peaks at 288.49 and 351.76 cm^-1 are doubly degenerate, which also shown in Figure 3 where the branches intercept at the frequencies at k-point L.

Figure 4. Phonon density of states vary with shrinking factor, 1st row 1; 2nd row 2, 4 and x; 3rd 16, 32 and 64

Figure 5. Illustration between the number of k points and the grid size in 2D; in a 2x2 grid, there are four k-point included but 64 points in an 8x8 grid

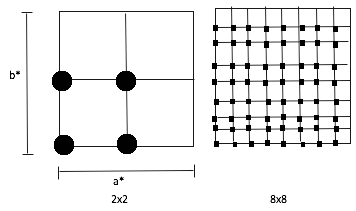
As the shrinking factor increase in Figure 4, the DOS graphs change from multiple sharp peaks to a smooth curve. The larger the shrinking factors, the more the k-points in the reciprocal space will be included in the calculation, so more vibrational frequencies of MgO are covered. The concept is illustrated in Figure 5, by using 2D grids as examples, each black dot correspond to a k point, in a 2x2 grid four k-points were taken into account, whilst 64 k-points were included in an 8x8 grid and they are identical by translation. It also means that as the shrinking factors increase, the ‘resolution’ of the Brillouin zone become higher and therefore more k-points were included in the calculation to find out the accessible vibrational energy levels.

To carry on the thermal expansion investigation in MgO, the grid size should be large enough to generate an accurate representation of the system by covering as many vibrational frequencies as possible. But one concern is the larger the grid size, the longer the calculation time especially when the shrinking factor went up to 64, the calculation was about 30 minutes longer compare to the chrinking factor of 32. By comparing the DOS in Figure 4, the curve of 32 and 64 are observably identical, so the grid size of 32x32x32 would provide a close approximation to the DOS of an infinite lattice and more likely to give accurate results a minimal calculating time.

Helmholtz Free energy

The thermodynamic representation of Helmholtz Free energy (A) is given by

$A(T,V)=U(V)-TS(T,V)$ (Equation. 1)

Where

A(T,V) corresponds to volume and temperature dependence of Helmholtz free energy

T is the temperature

S is the entropy of the system and it is temperature and volume dependent

U internal lattice energy and the full expansion is (equation 2)

$U$= $E_0+\frac{1}{2}\sum _{\mathbf{k},j}\hslash {\omega }_j{,}_k$ (Equation. 2)

where

E₀ is the zero point energy

S Entropy, the internal degree of freedom, taken from Taylor expansion up to the second term.

j band number in volume V

Further more frequency is defined by

${\omega }_k=\sqrt{\frac{4J}{M}}sin\left(\frac{ka}{2}\right)$ (Equation 3)

Overall the full expansion of A is

$A=E_0+\frac{1}{2}\sum _{\mathbf{k},j}\hslash {\omega }_k{,}_j+k_{B}T\sum _{\mathbf{k},j}ln[1-exp(\frac{-\hslash {\omega }_j{,}_k}{k_{B}T})]$ (Equation 4)

In the GULP calculation, quasi-harmonic approximation model was used to compute the sum of the vibrational modes in the lattice with the given k grid size of 32. As mentioned in the previous section, the larger the grid size, the k-points and band were included, therefore more vibrational levels would be included in the sum during the calculation.

Free energies were computed with increasing shrinking factors and the results have been Tabulated in table 1 and plotted in Figure 6

Table 1. Free energy (or entropy) varies with grid size

i	Shrinking Factor	Helmholtz Free Energy A (eV)	|A64 - Ai | (meV)	Ai - Ai+1 | (meV)
1	1	-40.930301	3.8180	3.6920	Figure 6: Free energy against shrinking factor
2	2	-40.926609	0.1260	0.1590
3	4	-40.926450	0.0330	0.0280
4	8	-40.926482	0.0050	0.0040
5	16	-40.926482	0.0010	0.0010
6	32	-40.926483	0.0000	0.0000
7	64	-40.926483	n/a	n/a

From Figure 6, it shows that the Helmholtz free energies (i.e the phonon energies) were getting more positive as the grid size increases. As the grid size increase, more k-points are taken into account to in the free energy calculation. Therefore an infinitely large grid size is supposed to get a very accuracy free energy calculation. However, consider that the calculation time gets longer as the grid becomes larger, so it is used to obtain a grid where the free energy starts to get converge. From table, the ΔA correspond to the calculation accuracy and it shows that the free energy approach as the grid size increase and converge at the shrinking factor at 32, which further proven the shrinking factor of 32 is a good approximation of an infinite lattice of MgO. Either |A₆₄ - A_i | or | A_i - A_i+1 | can be used to find out the accuracy of the free energy with the given shrinking factor, the former is more suitable if the calculation time towards the value of convergence is short. A shrinking factor of 2 gives accuracy to 1 meV and 0.5 meV. Whilst, shrinking factor of 4 starts to give an accuracy to 0.1 meV

Thermal Expansion

Figure 7. Harmonic, Anharmonic and Qusai harmonic model

Quasi-harmonic approximation exploits the phonon vibration in solid state to describe volume-dependent thermal expansion at constant pressure. The origin of thermal expansion is from anharmonic vibration of phonon which as the temperature increase. At 0=K, the MgO lattice is in its only perfect conformation due to Boltzmann distribution and the separation of the bond Mg-O sits at the equilibrium. It also has the most negative potential energy and is illustrated at the minimal point of Lennard-Jones potential curve in Figure 7. As the temperature increase, the phonons in the lattice have more kinetic energy and the Mg-O bond to vibrate away from the equilibrium and result in gaining potential energy. The rise in energy arises from the repulsion (bond shortening) and attraction (bond lengthening) as the bonds vibrate, thus increase in cell volume. Furthermore, the entropy (disorderness) also increases because of the population of phonons in higher vibrational energy level and the physical displacement of the atoms from the equilibrium.

In order to obtain free energy and other parameters, the anharmonic model is simplified to a quasi-harmonic model which assume that all the bonds in the MgO lattice vibrate harmonically with a restoring force after bonds resemble two balls attached at the end a spring. Thermal expansion of MgO was investigated from 0 to 3000K, the optimised Helmholtz free energy, cell volume and cell parameters were recorded in Table 2 and plotted against temperature from Figure 8 to 10.

From Figure 8, the free energy became more negative as the temperature increased. The relationship can be deduced from Equation 1, it suggesting the entropy of the lattice increased as there was more thermal energy provided to the system when increasing the temperature, therefore more kinetic energy for atoms for vibration to different k-points. In addition, the lattice parameter increased as the temperature increased, which suggests the MgO lattice expanded after heating.

Table 2. Free energy, cell volume and lattice parameter at different temperature from QH approximation

Temperature (K)	Helmholtz Free Energy A (eV)	Cell Volume (Å3)	Lattice Parameter (Å)
0	-40.0919	18.8365	2.9866
100	-40.9024	18.8365	2.9867
200	-40.9093	18.8562	2.9876
300	-49.9281	18.8900	2.9839
400	-40.9586	18.9325	2.9916
500	-49.9994	18.9801	2.9941
600	-41.0493	18.0312	2.9968
700	-41.1971	19.0851	2.9994
800	-41.1719	19.1413	2.0056
900	-41.2430	19.1996	3.0056
1000	-41.3198	19.2600	3.0089
1500	-41.7749	19.5952	3.0261
2000	-42.3237	20.0030	3.0470
2500	-42.3237	20.5476	2.0743

Figure 8 Free energy against Temperature	Figure 9, Cell parameter against temperature

The increase of cell paramet with the temperature is a sign of thermal expansion. From the Figure 10, the rise of the volume in a quadratic fashion from 0 to 500 K. From 600 to 1000K, the volume increases proportionally to the increase of temperature. However as the temperature increase further, the increase in volume deviates from linearity. In order to find out the coefficient of thermal expansion of the MgO under Quasi-Harmonic approximation, Cell volume against temperature from 0 to 2500 K was plotted

Figure 10 Cell volume against temperature from 0 to 2500 K

$\alpha =\frac{1}{V_0}{\left(\frac{\partial V}{\partial T}\right)}_P$| (Equation 5)

Where V₀ is the initial volume of the cell and in this MgO it equals to 18.6804 ų

${\left(\frac{\partial V}{\partial T}\right)}_P$ is change of volume as the temperature increase. The gradient of the line of best fit in Figure 10 which is 4.468x10^-4 ų K^-1

By plotting the line of best fit in graph, the thermal coefficient is 2.3918 x 10 ^-5 K^-1. The slope of the graph is a key factor determining a thermal coefficient. however in the Quasi- Harmonic approximation, cell volume increase in an inconsistent fashion. Therefore figure 11 to figure 13 were plotted to obtain the equations that describe the line of best fit in three temperature range.

Figure 11, Cell volume against temperature from 100 to 500 K	Figure 12, Cell volume against temperature from 0 to 1000 K	Figure 13 Cell volume against temperature from 1500 to 2500 K

The thermal expansion coefficient was tabulated in Table 3

Table 3. Thermal expansion coefficient at different temperature

Temperature (K)	α x10-5(K-1)	α x10-5(K-1) from literature	% difference from expt and lit (%)
100-500	1.9461	3.12	38
600-1000	3.0632	4.23	28
1500-2500	4.5720	5.13	11

The thermal expansion coefficients were taken as an average at the given range of temperature. From the percentage difference between literature and experimental values. Experimental values from GULP simulation are closer to literature from the temperature at 600K to 1000K. Even though the thermal expansion has the lowest % difference between experimental and literature value in the range of 1500 to 2500 K, it has to consider that the cell volume deviated compare to the low temperature. Overall, the accuracy of the α is low in the quasi-harmonic approximation. Furthermore, there was no output for MgO at 3000K as the cell was said to be unphysical cell dimension. It is believed that the vibration of the atoms are very large when it was heated close to its melting point, which is 3125 K. It is because the assumption of harmonicity fails at high temperature. The phonons vibrate in a more anharmonic fashion at high temperature. To obtain a more accurate result a high temperature, dissociation should be considered in the calculation.

CaO, Zeolite and LIthium

By applying the trend and theory, we can predict the optimal grid size for CaO will be similar to MgO because their size of unit cells are similar. Compare to MgO, CaO has the same charge and is also a FCC lattice. The lattice parameter of CaO is 4.8108Å and lattice as the MgO 4.273 Å. Even though the lattice parameter of CaO is larger because of the larger ionic radii of calcium, it is expected they will have a very similar the intermolecular orbital interaction because they have a close unit cell size, therefore the grid size of 32 will be able to predict the physical properties in CaO.

On the other hand, for materials, such as Zeolites which consists of aluminium and silicon, that have a larger size of unit cell, a smaller grid size will be enough to give a good approximate for the whole lattice. Given that the relationship of size between real and reciprocal is $a^{*}=\frac{2\pi }{a}$, where 'a is the lattice parameter. from this relationship, a* gets smaller as the lattice parameter increase. Therefore a smaller grid size (i.e. fewer k-points) will be enough to find out all the DOS.

Look at metallic material such as lithium, the presence of electrons across the whole system allows conductivity. There is a overlap of electronic bands and have a greater contribution to the overall energy of the material. Whereas compare to vibrational modes in the system, which is relatively flat and has less contribution to the overall energy of the material. In order to find all the electronic levels, more k-points should be screened therefore a larger shrinking factor than 32 is required. meaning a longer calculation will be required to complete the simulation.

Molecular Dynamics

Molecular dynamic is another approach to find out the vibrational modes in lattices, which simulates the motions of the atoms that are close to reality. the Newton’s second law, Force=mass x acceleration) was computed. In the simulation, atoms in the lattice follow the trajectories as they are in the real lattice.

In GULP, the force of the atoms in the lattice was firstly computed, next to find out the acceleration using the relationship of a=F/m. An isothermal ensemble was used in this investigation, which means the number of atoms (N), pressure (P) and tmeperature (T) are the constrain of the system. As the whole simulation is a time-step process, the velocities (V) and positions (R) of the atoms are updated by V_new = V_old + a * dt followed by R_new = R_old + V_new * dt respectively. Repeat until average properties including energy, temperature and lattice volume converge. dt is the timestep, the length of time should be compromised between accuracy of averaging and calculation time efficiency. As the calculation of molecular dynamic is relatively long compared to 10^-15 fs was set which allowed about10 steps along at each given vibration. In this investigation, a supercell, which contains 32 MgO units, was used. This size is large enough to allow flexibility for vibration, whereas only k-point (0,0,0) would be included and only in-phase vibration would be allowed if only one single unit of MgO was used. Since the static system remains identical regardless the size of the lattice, therefore more vibrational modes can be summed with a 32-unit lattice which is large enough to mimic the real infinite structure of MgO.

Finally, the physical properties can be obtained from the time averages of the behaviour at each given temperature. The last average lattice volume at each temperature was taken and divided by 32 in order to find out the cell volume after thermal expansion. The results were tabulated in Table 4 and plotted in Figure 14. From Figure 14 the cell volume increased linearly as the temperature increased from 300K to 3000K.

Table 4, Cell volume at different temperature in molecular dynamic calculation

Temperature (K)	Cell Volume (Å3)
300	18.8406	Figure 14. Plot of Cell volume against Temperature for MD Calculations
400	18.8809
500	18.9300
600	19.0011
700	19.0627
800	19.1225
900	19.1791
1000	19.2228
1500	19.5003
2000	19.8319
2500	20.2384
3000	20.6197

The kinetic energy of the system increase as the temperature increase. So the molecules in the lattice have a faster motion with greater velocity. The direct proportional relationship between temperature and the average velocity is given by

$\frac{1}{2}{k}_{b}T=<\frac{1}{2}m{v}^2>$ Equation 6

The velocity is the average of velocity at each timestep m is the mass of the lattice k_b

the thermal expansion coefficient can also be calculated by Equation5 with the same V₀ of 18.6801ų. the gradient in the DM model is 6.5004x10^-4 ų K^-1 and α = 3.4799x10^-5 K^-1 .

Comparison between Qusai Harmonic model and Molecular Dynamics

In Figure 15, Cell Volumes were plotted against Temperature in both approaches. It is clearly shown that from 300 K to 1000K, both approaches have similar linear increase. As the temperature increase beyond 1000K, the curve for QH starts to deviate from linearity when the curve for MD remains linear increase with the rise in temperature.

Figure 15. Cell Volume against Temperature in QH and MD models

The deviation of the cell volume in Quasi-Harmonic model can be accounted by the failure of assumption for harmonicity at high temperature. At high temperature, the bond elongation is has a longer lifetime than bond shortening. Meaning the restoring force is relative weaker when the temperature gets higher, especially when the temperature rose close to the melting point of the lattice. The approximation assumed there is infinite expansion in the lattice but in fact, the calculation should have taken bond dissociation into account in order to obtain more accurate values at high temperature.

In the Qusai-harmonic model, a quantum mechanic model was used where the zero point energy is taken into account, therefore it is more accurate to find out the coefficient at low temperature. Whereas molecular dynamics uses a classical model of the dynamics of the molecules in the lattice, and the zero point energy is not taken into account overall. therefore the calculation at low temperature is not accurate. But at high temperature, the zero-point energy is relatively small therefore it is neglectable and it is more accurately predicted by molecular dynamics and the structure of the lattice is less dependent on the temperature.

Conclusion

GULP was used to investigated the thermal expansion of MgO. The lattice energy of the MgO sample is -41.0753 eV, which is slight more negative compare to the literature by 3%. Anharmonicity was neglected in Quasi- Harmonic approximation. a shrinking factor of 32 give the optimal grid size in the reciprocal space in the unit by compromising between the shortest calculation time and the structure close to the real infinite MgO lattice. In the calculation of Halmotlz free energy in QH used the relationship in thermodynamics, the free energy of a primitive cell is -40.926483eV in a 32x32x32 grid. During the simulation, as the temperature increase, the free energy became more negative because of the increase of entropy. In addition, it is obvious sign of thermal expansion because of the increase in cell volume and lattice parameter. the overall thermal expansion coefficient is 2.3918 x 10 -5 K^-1. However, the expansion diverged from linearity as the temperature increase close to the melting point of MgO, which suggested that dissociation in the anharmonic model should be considered.

On the other hand, molecular dynamics is another approach to calculate the thermal expansion coefficient. By using a supercell which consists of 32 unit of conventional cells of MgO. It recorded the averaged parameter of the cell as the temperature. the coefficient from this model is 3.4799x10-5 K^-1 , whcih larger than the QH approach. It is able to predict the behaviour of the MgO lattice because it is less temperature dependence.

As there is a significant difference from literature and experimental value in the QH. It is suggested that a larger grid in the reciprocal space is required to improve the accuracy. The simulation should have been run at least three times to obtain the error from the calculation.