Rep:Mod:CHEM121500122000
Yr 3 Physical Computational Module
Sebastian Strudley
Part 1: The Cope Rearrangement
The Cope Rearrangement is a [3,3] sigmatropic rearrangement of 1,5-hexadiene. It is an example of a pericyclic reaction that undergoes a concerted, cyclic transition state. The reactant and product of the cope rearrangement are chemically identical.
There has been a large degree of study of the Cope Rearrangement. For example, in 1971 Hoffmann and Stohrer published a paper investigating a variety of rearrangements based on the Cope rearrangement.[1]

Optimizing energies of 1,5-hexadiene
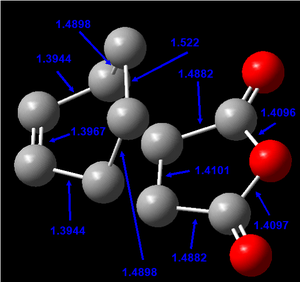
- 1,5-hexadiene with an anti linkage about the central four C atoms was optimized using the HF/3-21G level of theory. The resulting structure corresponded to the anti2 structure within [Appendix 1] of the experimental script. The symmetry of the structure, and its energy was obtained from the calculation.
- A further anti conformation (anti4) was obtained, but this was higher in energy than the previously found conformation.
- Conformational studies have previously been completed on 1,5-hexadiene. In 1994 calculations were reported at the MP2/6-31G* level which showed 'little energy difference between the anti and gauche conformations'. This result was found in this exercise, with only a few kcal / mol difference in energy between the conformations.
- The group also reported 10 distinguishable conformations, with a gauche conformer having the lowest in energy. Further to this they report that 'an attractive interaction may be present between the π orbital and the vinyl proton'.[2] If the central four atoms in 1,5-hexadiene are modelled as butane, an antiperiplanar arrangement of these atoms (as in the anti conformations below) would be expected to be lowest in energy. Somewhat suprisingly, for 1,5-hexadiene the lowest conformation exists with a gauche orientation of the central 4 atoms. The stabilising interaction between a π orbital and vinyl protons mentioned above could explain this phenomenon.
Energies were optimized as below:
Theory: HF/3-21G
Method: Hartree Fock
Basis Set: 3-21G
| Conformer | Geometry | Point Group | Energy (Hartrees) | Energy (kcal/mol) | Relative Energy (kcal/mol) | Log File |
|---|---|---|---|---|---|---|
| Anti2 | 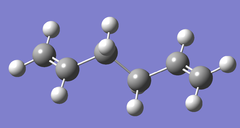 |
Ci / C1 | -231.69253 | -145389.29 | 0.0816 | File:Anti2 .LOG |
| Anti4 |  |
C1 | -231.69097 | -145388.31 | 1.0605 | File:Anti4 .LOG |
| Guache2 |  |
C2 / C1 | -231.69167 | -145388.75 | 0.6212 | File:Guache2 .LOG |
| Guache3 | 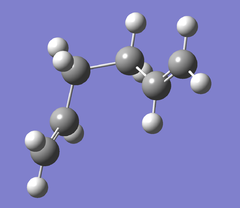 |
C1 | -231.69266 | -145389.37 | 0 | File:Guache3 .LOG |
The Anti2 conformation.
- The anti2 conformation was further analysed at a higher level of theory (B3LYP/6-31G*). The results were compared to those obtained from the earlier calculations. Also, an IR spectrum was simulated.
Comparison between the HF/3-21G and B3LYP/6-31G* levels of theory.
- Little change in geometry was observed between the two calculations, however there are significant differences in the energies predicted by the two levels of theory.
| Theory | Geometry View 1 | Geometry View 2 | Point Group | Sum of electronic and thermal energies (Hartrees) |
Log File |
|---|---|---|---|---|---|
| HF/3-21G |  |
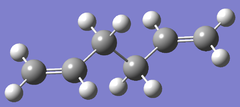 |
Ci/C1 | -231.532566 | File:Anti2 .LOG |
| B3LYP/6-31G* |  |
 |
Ci/C1 | -234.461857 | File:Anti2B3LYP .LOG |
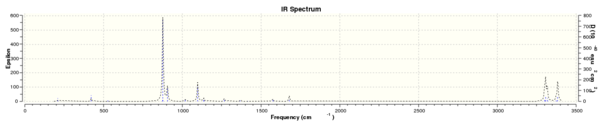
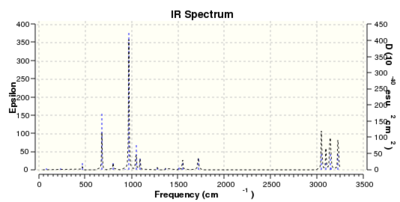
IR Data
- The results of the IR calculation showed only real vibration frequencies (i.e. none reported with negative values). This is expected, as the spectrum was calculated for a 'real' molecule rather than a transition state. Some of the vibrations have been animated and are shown below.
 |
 |
 |
Thermochemical Data
- The thermochemistry data for the anti2 conformation at the B3LYP/6-31G* level of theory is shown below. The data was collected from this log file: File:Anti2B3LYP .LOG
|
|
Optimizing the chair and boat TS structures
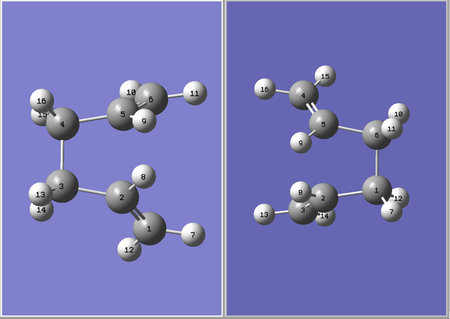
(a) Allyl (CH2CHCH2) fragment optimization
- In GuassView, a 3 carbon fragment was drawn and optimised at the HF/3-21G level of theory.
(b) Optimising to a TS (Berny) for a chair TS.
- A chair TS was approximated by positing two of the allyl fragments previously optimised in (a) with the allylic ends at a distance of around 2.2 Å apart.
- The resulting structure was obtained. The IR spectrum, and an animation of the imaginary vibration (negative frequency) are shown below.
- The log file from the calculation is avaliable here. File:Partb .LOG
(c) Optimising the structure using the frozen coordinate method.
- This part was not attempted due to the recent update to the Guassian software - please see script.
(d) Freezing the forming bond lengths using the redundant coordinate editor
- An optimisation calculation was attempted by fixing the bond distances that are broken / made to 2.2 Å.
- The input file was set up as per the screenshots below.
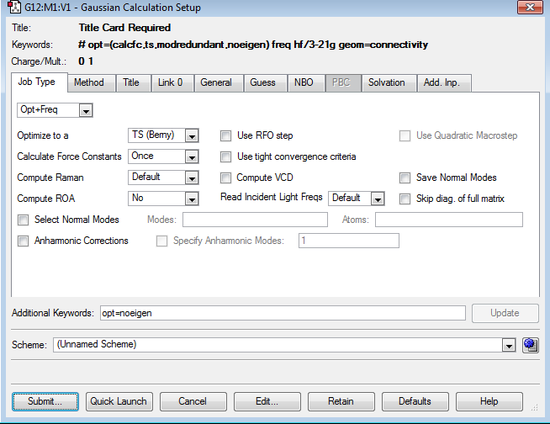 |
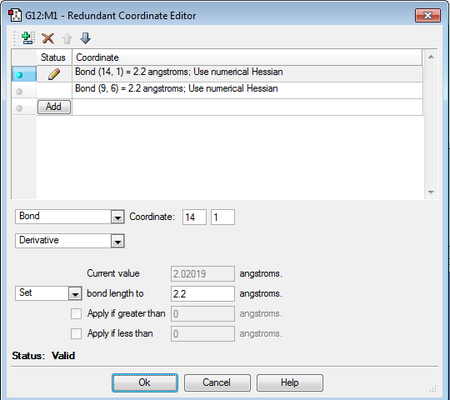 |
Unfortunately when the output file was analysed, the bond lengths of the forming bonds (2.025 Å - see below) were the same as those obtained in part (b), indicating that the attempt to fix the bond forming lengths was not successful.
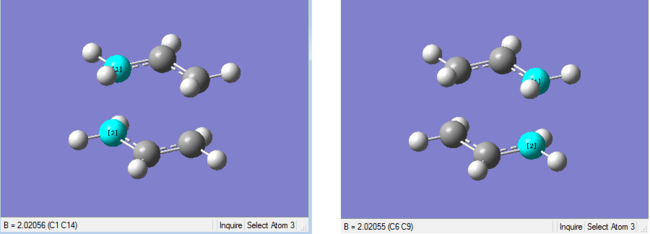
(e) Optimising the boat TS structure, using the QST2 method
- The anti2 conformation obtained from a calculation at the B3LYP/6-31G* level was used as a starting point.
- Care was taken to ensure the atom numbering was correct for reactant to product.

- A QST calculation using Opt + Freq and TS (Berny) was attempted. This calculation failed.
- A further calculation was run with modified conditions in order to locate the boat transition state. The following changes to both reactant and product molecules were stipulated to achieve this:
- C2-C3-C4-C5 dihedral angle: 0°
- C2-C3-C4 angle: 100°
- C3-C4-C5 angle: 100°
|
 |
 |
- A single imaginary vibration (v = -840.1 cm-1) was observed in the output file from the calculation. This vibration is animated below:
 |
- As the calculation was successful, it suggests that the reactants and products were close to the TS, achieved by the stipulations above.
(f) Intrinsic Reaction Coordinate Method
The chair TS appears to connect the guache3 conformers whilst the boat TS appears to connect the gauche2 conformers.
1. Running a minimization from the last point on the IRC

This energy corresponds fairly well to that of -234.460913 found for the anti2 conformation of the reactant.
2. Restart the IRC with a larger number of points
3. Calculating the force constants at each step
| ||||||||||
(g) Calculating the activation energy for the reaction using both transition states
The activation energies for the reaction were then calculated using both the chair and boat transition states at the B3LYP/6-31G* level of theory.
Summary of energies for calculations at different levels of theory (Hartrees)
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS | -231.619322407 File:Chair .LOG |
-231.466705 [Script] |
-231.461341 File:Chair .LOG |
-234.556983 File:Chair b3lyp.LOG |
-234.414919 [Script] |
-234.409009 File:Chair b3lyp.LOG |
| Boat TS | -231.6028024 File:Boat .LOG |
-231.450929 [Script] |
-231.445305 File:Boat .LOG |
-234.5430931 File:Boat b3lyp.LOG |
-234.402340 [Script] |
-234.396008 File:Boat b3lyp.LOG |
| Reactant (anti2) | -231.692535 File:Anti2 .LOG |
-231.539539 [Script] |
-231.532566 File:Anti2 .LOG |
-234.611710 File:Anti2 b3lyp.LOG |
-234.469203 [Script] |
-234.461857 File:Anti2 b3lyp.LOG |
- When the geometries for the two calculation levels are compared, significant changes in energies are reported. However, there is little change in geometries of the transition states observed.
Converted energies for different levels of theory (kcal / mol) compared to experimental data
- Energies were converted using an online converter ( for high accuracy conversion avaliable [here]. The data is reported to 3.d.p as evidence the calculations have been completed...
| Theory | HF/3-21G | B3LYP/6-31G* | Experimental | ||
| Temp. | 0 K | 298.15 K | 0 K | 298.15 K | |
| ΔE Chair TS | 45.704 | 44.694 | 34.064 | 33.163 | 33.5 ± 0.5 |
| ΔE Boat TS | 55.604 | 54.757 | 41.957 | 41.321 | 44.7 ± 2.0 |
The data for the chair TS at the B3LYP/6-31G* level, at 298.15 K agrees very well to the literature value. The data obtained for the boat TS does not agree as favorably. This suggests that the TS calculated for the boat is less accurate than that for the chair.
It can clearly be seen that the data at the B3LYP/6-31G* level agrees much more accurately to the experimental, than that for the HF/3-21G level.
Effect of temperature on the activation energy of the reaction
- The FreqChk utility available in Guassian09W was used to obtain data at different temperatures.
- The partition function energies are reported, as there was no thermal correction to Energy avaliable in the output in command prompt - see this file which is a copy of the command prompt data: File:Freqchk315kboat.txt
The results are summarized below:
|
| ||||||||||||||||||||||||||
The data collected appears anomalous - the activation for the chair TS is higher than that for the boat, which is in contrast to the results obtained above.
Part 2: The Diels Alder Cycloaddition

The Diels Alder cycloaddition[3] has and still is the subject of a huge degree of scientific. Indeed, since the beginning of 2014 over 1,000 scientific papers have been published on the subject! Diels Alder was a revolutionary C-C bond forming reaction (to make 6-membered rings) which is of huge importance in synthetic chemistry. Although typical Diels Alder reactions require an electron rich diene and an electron rich dienophile, Inverse electron demand Diels Alder reactions are well known. The reaction is pericyclic process with a concerted cyclic transition state.
The synthetic usefulness of the Diels Alder is not limited exclusively to carbon only frameworks, but also encompasses hetero-Diels Alder reactions which allow the formation of a number hetereocylic compounds. Interestingly a rate acceleration on Diels-Alder reactions has been reported when they are carried out in water. This is of great interest to chemists, especially in the age where the reduction of hydrocarbon solvent usage is essential.[4]
(i) Cis-butadiene
Optimization of geometry
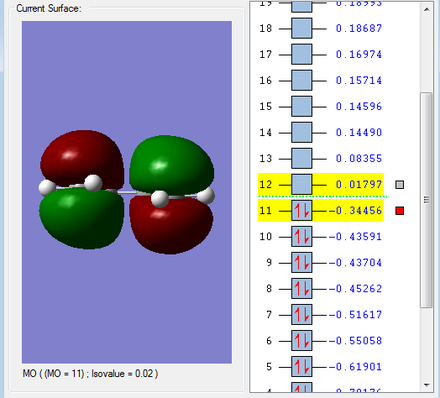
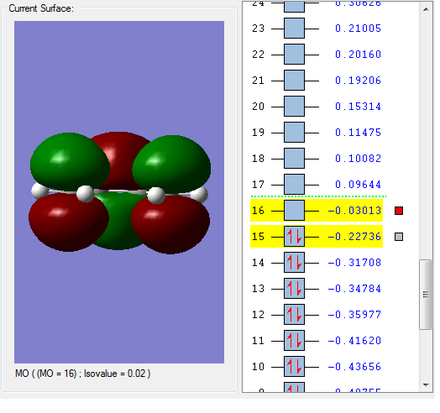
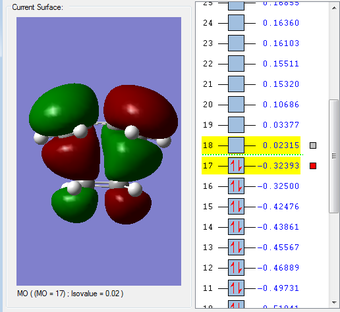
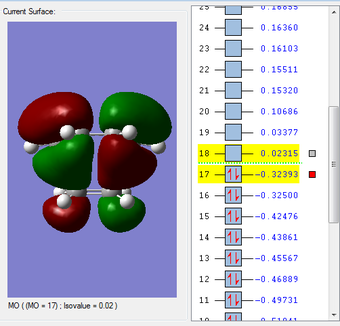
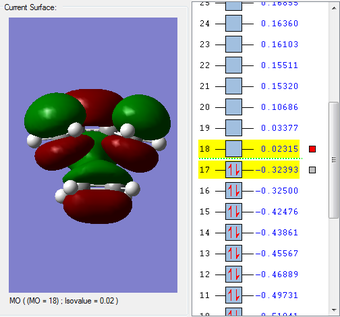
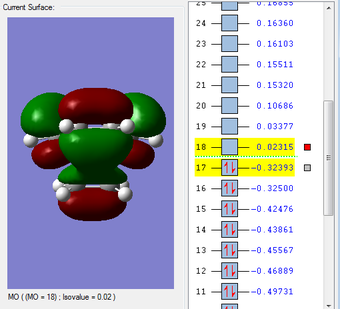
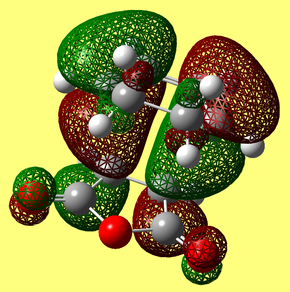
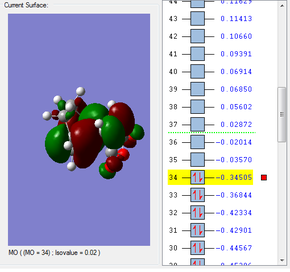
HOMO & LUMO Molecular Orbitals
The HOMO is antisymmetric with respect to the plane of the molecule, whilst the LUMO is symmetric. |
(ii) Computation of the Transition State geometry for the prototype reaction and an examination of the nature of the reaction path
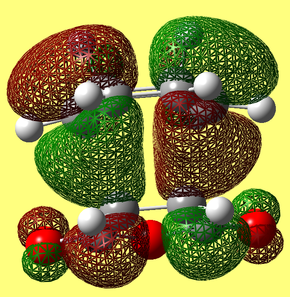
HOMO & LUMO Molecular Orbitals
a) HOMO
b) LUMO
The HOMO is antisymmetric with respect to the plane, whilst the LUMO is symmetric with respect to the plane.
Molecular Orbitals
The HOMO at the TS is asymmetric.
Whether the Diels-Alder is normal or inverse electron demand will determine whether the HOMO is located on the diene and the LUMO on the dienophile or vice versa. In this case the reaction is likely to be normal electron demand, with the HOMO located on diene (cis-butadiene) and the LUMO located on the dienophile (ethylene). The LUMO of cis-butadiene was shown to be symmetric in the previous section and the HOMO of ethylene (π bonding orbital) is also symmetric. These orbitals can therefore overlap effectively. Conversely, if the reaction were to proceed by an inverse electron demand, this is still allowed by orbital symmetry. The HOMO of cis-butadiene and the LUMO of ethylene (π* antibonding orbital) are both antisymmetric. The reaction is allowed, as both the HOMO and LUMO are of the same symmetry and therefore overlap efficiently.
Geometry of the Transition State
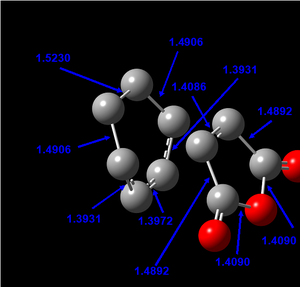
The bond lengths of the partly formed C-C bonds in the transition state were measured as 2.20997 and 2.20899 Å. These bond lengths are very similar and are essentially equivalent when analysed at 2 d.p (2.21 Å). This provides evidence for the concerted, pericyclic nature of the Diels-Alder reaction (i.e. both bonds are formed simultaneously in a cyclic transition state). These bond lengths agree fairly well to those reported in literature for the transition state of this reaction of 2.27 ± 0.25 Å.[5].
A typical C-C bond length for sp3 hybrididised carbon atoms in the -CH2-CH2- functionality is 1.524 Å.[6] A typical C-C bond length for sp2 hybrididised carbon atoms in the -CH=CH- functionality is 1.478 Å.[6] The Van der Waals radius of a carbon atom has been reported as 1.70 Å.[7] The bond lengths obtained for the transition state appear to be significantly greater than the expected C-C radii for sp3 or sp2 hybridised C-C bonds, but within 2 x the Van der Walls radius (2 x 1.70 = 3.40 Å). This suggests there is interaction between the atoms in the transition state which is expected.
Vibration that corresponds to the reaction path at the TS
The formation of the two bonds in the TS (corresponding to the imaginary vibration) appears to be synchronous when animated above. However, the lowest energy vibration appears to show a 'waggling' type motion between the two carbons corresponding to the ethylene reactant and the butadiene framework. In most Diels-Alder reactions, C-C bonds form very shortly (within 50 femto seconds [fs]) of the TS. The two different C-C bonds tend to form within 5 fs of each other which means that any bond stretching vibrations do not occur on a timescale which can prevent the bond forming being synchronous.[5]. |
(iii) Study of the regioselectivity of the Diels Alder Reaction
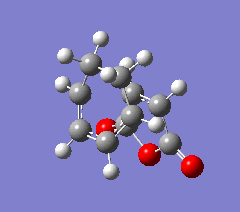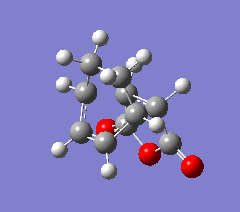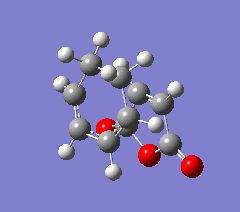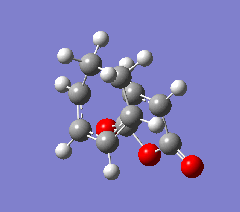
a) Exo TS
b) Endo TS
An imaginary vibration (v= - 806.15 cm-1) was reported for the calculation. This vibration is animated below:
Questions
The endo and exo TS structures were further optimised sequentially at the HF/3-21G' and then B3LYP/6-31G* levels in order to obtain representative values for the energies. The log files and energies obtained are displayed in the table below. In order to check that a TS had indeed been obtained from these re-optimisations, animated immaginary vibrations are also shown in the table for the calculations at the B3LYP/6-31G* level. The endo TS is lower in energy than the exo TS by around 2.59 kcal/mol. In this case, it is the kinetic transition state.
As these sets of interactions occur on a distance smaller than the VdW radius, it can be seen the exo form experiences greater unfavorable steric interactions, whilst the endo form undergoes favorable secondary orbital interactions which stabilises it. Also, in both the exo and endo TS, the C-C bond distances of the forming bonds are similar - this is evidence for the concerted, pericyclic nature of the TS.
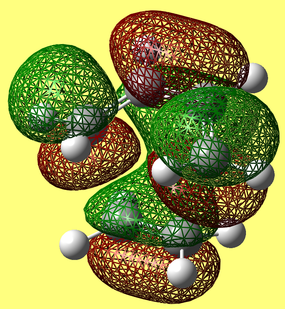
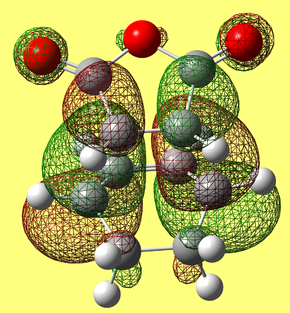
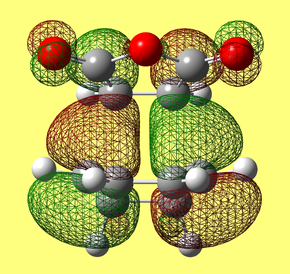
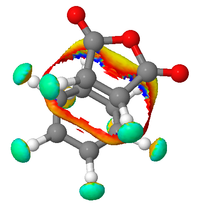
The transition states for both the endo and exo forms were subjected to a NCI (Non-covalent-interactions) analysis. Areas marked green are weakly attractive, in blue strongly attractive, in yellow are weekly repulsive and in in red are strongly repulsive.
The secondary orbital overlap effect is an effect that has been envoked to explain the selectivity of the Diels Alder reaction for the endo isomer over the exo one. The theory is that there are other orbital overlap interactions that are significant in the transition state other than the HOMO - LUMO interactions. It has previously been reported that for certain reactions, these secondary orbital overlap interactions are only present in the endo TS, meaning it is formed faster and thus made preferntially.[8] It can be seen in the endo TS above, that there is a nodal plane between the two fragments that compose the transition state. As HOMO LUMO orbital overlap is thought to be a prerequisite for getting a particular isomer, this cannot explain why the reaction proceeds. Secondary orbital overlap must therefore be envoked to explain why the endo form, the kinetic product predominates. |
(iv) What effects have been neglected in these calculations of Diels Alder transition states?
|
References
<references>
- ↑ Roald Hoffmann , Wolf D. Stohrer, "Cope rearrangement revisited", J. Am. Chem. Soc., 1971, 93 (25), 6491-6948.DOI:10.1021/ja00754a042
- ↑ Benjamin W. Gung , Zhaohai Zhu , Rebecca A. Fouch, "Conformational Study of 1,5-Hexadiene and 1,5-Diene-3,4-diols", J. Am. Chem. Soc., 1995, 117 (6), 1783-1788.DOI:10.1021/ja00111a016
- ↑ Diels, O. .; Alder, K., "Synthesen in der hydroaromatischen Reihe", Justus Liebig's Annalen der Chemie, 1982, 460, 98–122.DOI:10.1002/jlac.19284600106
- ↑ Rideout, Darryl C.; Breslow, Ronald "Hydrophobic acceleration of Diels-Alder reactions", J. Am. Chem. Soc, 1980, 102(26), 7816.DOI:10.1021/ja00546a048
- ↑ 5.0 5.1 Kersey Blacka, Peng Liub, Lai Xub, Charles Doubledayc, Kendall N. Houkb, "Dynamics, transition states, and timing of bond formation in Diels–Alder reactions", Proceedings of the National Academy of Sciences, 2012, 109(32), 2860-5.DOI:10.1073/pnas.1209316109 Cite error: Invalid
<ref>tag; name "ja98253aasa32" defined multiple times with different content - ↑ 6.0 6.1 Frank H. Allen, Olga Kennard, David G. Watson, Lee Brammer, A. Guy Orpen, Robin Taylor "Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds", J. Chem. Soc., Perkin Trans, 1987, 2, S1-S19.DOI:10.1039/P298700000S1
- ↑ A. Bondi, "Van der Waals Volumes and Radii", J. Phys. Chem, 1964, 68 (3), S1-S19.DOI:10.1021/j100785a001
- ↑ Roald Hoffmann , Wolf D. Stohrer, "Steric effects vs. secondary orbital overlap in Diels-Alder reactions. MNDO and AM1 studies", J. Org. Chem., 1987, 52(8), 1469-1474.DOI:10.1021/jo00384a016
- ↑ Assadi, M.H.N, "Theoretical study on copper's energetics and magnetism in TiO2 polymorphs", Journal of Applied Physics, 2012, 113(23), 2860-5.DOI:doi:10.1063/1.4811539