Rep:Mod:CGIC24

NH₃

Calculation Method: B3LYP

Basis Set: 6-31G(d,p)

Final Energy: -56.55776873 au

RMS Gradient: 0.00000485 au

Point Group: C3V

N-H Bond Length: 1.01798 Å

H-N-H Bond Angle: 105.547 degrees

Item Table:

        Item               Value     Threshold  Converged?
Maximum Force            0.000004     0.000450     YES
RMS     Force            0.000004     0.000300     YES
Maximum Displacement     0.000072     0.001800     YES
RMS     Displacement     0.000035     0.001200     YES

File:CGreen NH3 optf pop.log

NH3

Vibrational Modes:

From the analysis, there are 6 vibrational modes which is to be expected from the 3N-6 rule where N=4, of which there are two pairs of degenerate modes, 2 and 3 along with 5 and 6. Modes 1,2 and 3 are bending modes, and then modes 4,5 and 6 are the stretching modes. Mode 4 is a highly symmetric stretch. Mode 1 is known as the 'umbrella' mode. None of the modes are symmetric, however, since modes 2 and 3, and 5 and 6 are degenerate this means there are 4 bands on the spectrum.

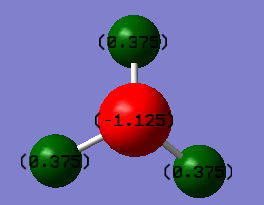
Figure 2 - Shows the relative charges on each atom in NH₃.

From the figure 2 above, the Nitrogen has a charge of -1.125 C and the Hydrogen's have a charge of +0.375 C. This is to be expected due to Nitrogen having a considerably higher electronegativity compared to Hydrogen, and so electron density is shifted towards the Nitrogen giving it a negative charge and leaving a positive charge on the Hydrogen's.

N₂

Calculation Method: B3LYP

Basis Set: 6-31G(d,p)

Final Energy: -109.52411287 au

RMS Gradient: 0.00002853 au

Point Group: D*H

N-N Bond Length: 1.10551 Å

N-N Bond Angle: 180 degrees (Linear)

Item Table:

        Item               Value     Threshold  Converged?
Maximum Force            0.000049     0.000450     YES
RMS     Force            0.000049     0.000300     YES
Maximum Displacement     0.000015     0.001800     YES
RMS     Displacement     0.000022     0.001200     YES

File:Cg1417 n2 optf pop.log

N2

Vibrational Modes:

Figure 3 - Shows the vibrational mode of N₂ and the associated frequency.

There is a single non-negative frequency that corresponds to a stretching mode.

H₂

Calculation Method: B3LYP

Basis Set: 6-31G(d,p)

Final Energy: -1.17853936 au

RMS Gradient: 0.00000017 au

Point Group: D*H

H-H Bond Length: 0.74279 Å

H-H Bond Angle: 180 degrees (Linear)

Item Table:

        Item               Value     Threshold  Converged?
Maximum Force            0.000000     0.000450     YES
RMS     Force            0.000000     0.000300     YES
Maximum Displacement     0.000000     0.001800     YES
RMS     Displacement     0.000001     0.001200     YES

File:Cg1417 h2 optf pop.log

H2

Vibrational Modes:

Figure 4 - Shows the vibrational mode of H₂ and the associated frequency.

This shows a single non-negative frequency which corresponds to a single stretching mode

Haber-Bosch Process

N₂ + 3H₂ --> 2NH₃

E(NH₃) = -56.55776873 au

2*E(NH₃) = -113.11553746 au

E(N₂) = -109.52411287 au

E(H₂) = -1.17853936 au

3*E(H₂) = 3.53561808 au

ΔE = 2*E(NH₃) - [E(N₂) + 3*E(H₂)]

  = -113.11553746 - [-109.52411287 + (-3.53561808)]

  = -0.0558065 au = -146.52 kJ/mol

This shows the reaction is exothermic as ΔE<0, so the ammonia product is more stable than the gaseous reactants.

ClF₃

Calculation Method: B3LYP

Basis Set: 6-31G(d,p)

Final Energy: -759.46531688 au

RMS Gradient: 0.00003817

Point Group: C1

Cl-F Bond Lengths: 1.72842 Å; 1.65136 Å F-Cl-F Bond Angle: 87.135 degrees

Item Table:

        Item               Value     Threshold  Converged?
Maximum Force            0.000064     0.000450     YES
RMS     Force            0.000031     0.000300     YES
Maximum Displacement     0.000191     0.001800     YES
RMS     Displacement     0.000142     0.001200     YES

File:Cg1417 clf3 optf pop.log

ClF3

Vibrational Modes:

From figure 5, there are six vibrational modes, which is to be expected from the 3N-6 rule for the non-linear molecule. Modes 1,2 and 3 correspond to the bending modes, and modes 4,5 and 6 correspond to the stretching modes.

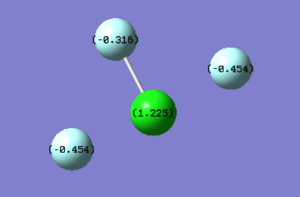
The photo above shows the charges on each atom within the molecule. Since Fluorine has a higher electronegativity than Chlorine, each individual Fluorine atom is expected to have a negative charge as it pulls electron density towards itself and away from the Chlorine atom, leaving behind a positive charge on the Chlorine. As expected the charges in the photo above support this. However, the F atom with the shorter Cl-F bond length (1.65136 Å) has a less negative charge compared to the Fluorine atoms involved in the Cl-F bonds with the longer bond length (1.72842 Å).

Molecular Orbitals:

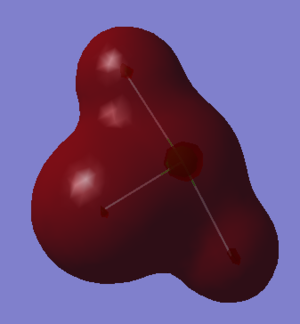
Figure 7 above shows the lowest energy molecular orbital of ClF₃. It is the linear combination of the 3s orbital on the Chlorine and the 2s orbitals on the Fluorine atoms, and each orbital overlaps in phase, meaning the MO is bonding with respect to all three Cl-F bonds.

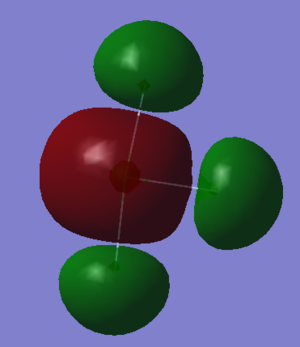
Figure 8 shows the fourth lowest energy MO. The MO is the corresponding antibonding MO of the lowest energy MO. There is destructive interference between the Chlorine 3s and the 2s orbitals on each Fluorine, and no overlap between these orbitals meaning the MO is anti-bonding with respect to all three Cl-F bonds.

Figure 9 shows the bonding MO formed from the linear combination of a 3p orbital which is in a perpendicular plane to the bonds between the atoms, and the 2p orbitals on the Fluorine in the same plane. All of the atomic orbitals are in the same phase, and so constructively overlap meaning the MO is bonding with respect to all three Cl-F bonds.

Figure 10 here is the highest occupied molecular orbital. It is the corresponding anti-bonding orbital with destructive overlap between the a 3p on the Fluorine and the 2p orbitals on the Fluorine atoms in the same plane. As a result, this means the MO is anti-bonding with respect to all three Cl-F bonds.