Rep:Mod:CCL2161
Ammonia
Key Information
Name of the molecule: Ammonia NH3
An optimization has been run with the structure of ammonia using GaussView 5.0.9 and the results are as followed:
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -56.55776873 a.u.
RMS Gradient: 0.00000485 a.u.
Point Group: C3v
N-H bond distance = 1.01798 Å
H-N-H bond angle = 105.741 degree
Ammonia |
Item Table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986287D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
A force value close to zero demonstrated that the lowest potential energy has been achieved and the structure has been optimized. The gradient of the potential energy v.s. distance slope is equaled to force.
Vibration Analysis
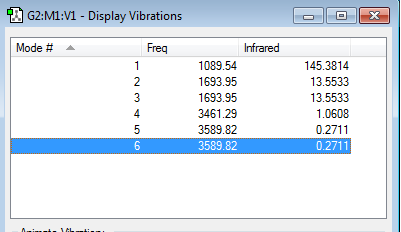
how many modes do you expect from the 3N-6 rule?
Trigonal Pyramidal molecule, hence 3N-6 rule is followed
As N=4, there would be 6 modes.
which modes are degenerate (ie have the same energy)?
mode 2&3 and mode 5&6
which modes are "bending" vibrations and which are "bond stretch" vibrations?
"bending" vibrations -- mode 1,2&3
"bond stretch" vibrations -- mode 4,5&6
which mode is highly symmetric?
mode 1 & 2 (symmetrical bend)
mode 4 (symmetrical stretch)
one mode is known as the "umbrella" mode, which one is this?
mode 1
how many bands would you expect to see in an experimental spectrum of gaseous ammonia?
Theoretically, there should be four band. As stretching vibration cause a much smaller change in dipole moment of the molecule, the two bands cause by mode 4, 5&6 might not be found in the real spectrum due to large signal to noise ratio. Greater the change in dipole moment, greater the absorbance of the band. Hence, in an experimental spectrum, only two band would be found.
Charge Analysis
It is expected that the more nitrogen would have a negative charge -- it has a lone pair of electron and is more electronegative, pulling the electrons from hydrogen. This make the charge of hydrogen positive.
calculation result
Nitrogen: -1.125
Hydrogen: 0.375

Hydrogen
Key Information
Name of the molecule: Hydrogen H2
An optimization has been run with the structure of hydrogen using GaussView 5.0.9 and the results are as followed:
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -1.17853936 a.u.
RMS Gradient: 0.00000017 a.u.
Point Group: D∞h
H-H bond distance = 0.74279 Å
H2 bond angle = N/A
Hydrogen |
Item table
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
A force value close to zero demonstrated that the lowest potential energy has been achieved and the structure has been optimized.
Vibration Analysis
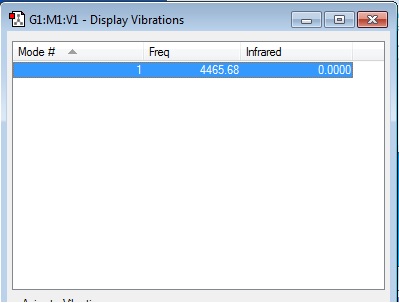
how many modes do you expect from the 3N-5 rule?
Linear molecule, hence 3N-5 rule is followed
1 modes -- symmetrical "bond stretch" vibrations
how many bands would you expect to see in an experimental spectrum of gaseous hydrogen?
This is a diatomic molecule with the two hydrogen atoms having the same electronegativity. Stretching of the molecule doesn't change the dipole moment of the molecule. Hence, 0 band is observed.
Charge Analysis
It is expected that both hydrogen would have a charge of zero as this is a diatomic molecule, implying that it is non-polar. Both hydrogen have the same electronegativiy.
calculation result
Hydrogen 1: 0.000
Hydrogen 2: 0.000
Nitrogen
Key Information
Name of the molecule: Nitrogen N2
An optimization has been run with the structure of nitrogen using GaussView 5.0.9 and the results are as followed:
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -109.52412868 a.u.
RMS Gradient: 0.00000060 a.u.
Point Group: D∞h
N-N bond distance = 1.10550 Å
N2 bond angle = N/A
Nitrogen |
Item table
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401004D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
A force value close to zero demonstrated that the lowest potential energy has been achieved and the structure has been optimized.
Vibration Analysis
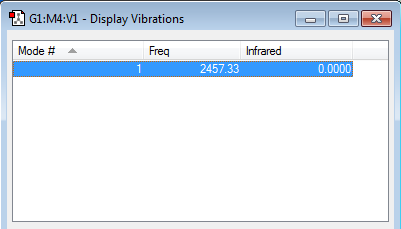
how many modes do you expect from the 3N-5 rule?
Linear molecule, hence 3N-5 rule is followed
1 modes -- symmetrical "bond stretch" vibrations
how many bands would you expect to see in an experimental spectrum of gaseous hydrogen?
This is a diatomic molecule with the two nitrogen atoms having the same electronegativity. Stretching of the molecule doesn't change the dipole moment of the molecule. Hence, 0 band is observed.
Charge Analysis
It is expected that both nitrogen would have a charge of zero as this is diatomic, implying that it is non-polar molecule. Both nitrogen have the same electronegativiy.
calculation result
Nitrogen 1: 0.000
Nitrogen 2: 0.000
Haber-Bosch Process: Reaction Energy
N2 + 3 H2 -> 2 NH3
E(NH3)= -56.55776873 a.u.
2*E(NH3)=-113.1155375 a.u.
E(N2)=-109.52412868 a.u.
E(H2)=-1.17853936 a.u.
3*E(H2)=-3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.05579074 a.u.
ΔE = 2625.5 x (-0.05577074) kJ/mol
ΔE = -146.47858787 kJ/mol
The literature value of ammonia is found to be -92 kJ/mol.[1]
With the literature value being a experimental value, the molecules might not necessarily all be in their lowest potential energy form in reality, leading to this great difference in energy.
Which is more stable the gaseous reactants or the ammonia product?
Ammonia product is relatively more stable as the enthalpy change of the reaction is negative. Overall, energy have been released.
My Choice of Small Molecule: Cyanide Ion
Key Information
Name of the molecul: Cyanide Ion (CN-)
An optimization has been run with the structure of hydrogen using GaussView 5.0.9 and the results are as followed:
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -92.82453153 a.u.
RMS Gradient: 0.00000704 a.u.
Point Group: C∞v
H-H bond distance = 1.18409 Å
bond angle = N/A
Cyanide Ion |
Item Table
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000005 0.001800 YES
RMS Displacement 0.000008 0.001200 YES
Predicted change in Energy=-6.650393D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1841 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
A force value close to zero demonstrated that the lowest potential energy has been achieved and the structure has been optimized.
Vibration Analysis
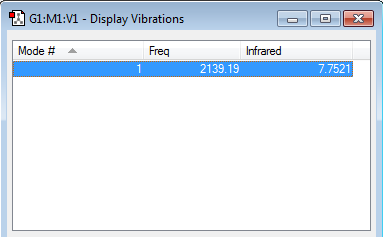
how many modes do you expect from the 3N-5 rule?
Linear molecule, hence 3N-5 rule is followed
1 modes -- symmetrical "bond stretch" vibrations
how many bands would you expect to see in an experimental spectrum of gaseous hydrogen?
Theoretically, 1 band should be observed due to the change in dipole moment from stretching as a result from the electronegatvity difference between carbon and nitrogen. However, the change in dipole moment is not significant (the electronegativity difference is relatively small and stretch tend to lead to less change in dipolemoment than bending), the absorbance value for the band is low. Hence, it is likely that this band would be loss in due to the high signal to noise level and 0 band is observed in the experimental spectrum.
Charge Analysis
The charge on nitrogen and carbon are both negation as the cyanide ion is -1 negative charge overall. As nitrogen is more electronegative than carbon (greater ability to attract electron towards itself), it would have a more negative charge than carbon. The sum of the charge of carbon and nitrogen is -1.
calculation result

Nitrogen: -0.754
Carbon: -0.246
Molecular Orbitals of Cyanide

M=1 is an occupied non-bonding orbital of nitrogen. It is essentially the 1s orbital of nitrogen. (It has the lowest energy among all other orbitals, -14.00393 eV. As the s orbital of carbon is found to be -9.86720 eV by Gaussian, it is expected that there would be no bonding between the two s orbitals. Nitrogen is more electronegative than carbon, hence its 1s orbital is deeper in energy.)

MO=4 is a σ* orbital with an energy of -0.10626 eV and there is two electrons occupying this orbital. It is formed by destructive interference of 2s orbitals from nitrogen & carbon and molecular orbital mixing with the σ* orbital formed by 2p. Hence, it has both bonding and anti-bonding characters. The molecular orbital mixing reduce the energy of this orbital, which makes it even deeper in energy. Hence, it is expected that electron from this orbital tend not to take part in reactions.


MO=5 and MO=6 are two occupied π orbitals with degenerated energy, -0.1698 eV. They are both bonding orbitals formed by constructive interference of 2p orbitals. The two orbitals have exactly the same shape, yet with different orientation. As the electronegative difference between carbon and nitrogen are not significant, the orbital looks rather symmetrical.

MO=7 is a σ orbital and the HOMO (Highest Occupied Molecular Orbital), formed by constructive interference of 2p orbitals. It has a rather high energy, quite close to zero, with two electron occupied, which make cyanide ion a very good nucleophile and Lewis base in organic reaction. The electrons can easily take part in reactions and donate to electrophile. Usually, it is expected that this orbital should have a lower energy than the π Orbital (MO=5 and MO =6). However, due to the molecular orbital mixing with the σ orbital formed by overlaps of 2s orbitals, this orbital have some anti-bonding character and hence high energy, -0.01857 eV.


MO=8 and MO=9 are two unoccupied π* orbitals with degenerated energy, 0.35435 eV. They are also the LUMO (Lowest Unoccupied Molecular Orbital) of the molecule. With a positive energy for LUMO, cyanide is a poor electrophile and poor Lewis acid. In both case, there's a greater electron density towards carbon, the less electronegative atom with higher energy atomic orbital than nitrogen.
Independence: Carbon Dioxide
Key Information
Name of the molecule: Carbon Dioxide CO2
An optimization has been run with the structure of carbon dioxide using GaussView 5.0.9 and the results are as followed:
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -188.58093945 a.u.
RMS Gradient: 0.000001154 a.u.
Point Group: D∞h
C=O bond distance = 1.16915 Å
O=C=O bond angle = 180 degree
Carbon Dioxide |
Item Table
Item Value Threshold Converged?
Maximum Force 0.000024 0.000450 YES
RMS Force 0.000017 0.000300 YES
Maximum Displacement 0.000021 0.001800 YES
RMS Displacement 0.000015 0.001200 YES
Predicted change in Energy=-5.259645D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1691 -DE/DX = 0.0 !
! R2 R(1,3) 1.1691 -DE/DX = 0.0 !
! A1 L(2,1,3,-2,-1) 180.0 -DE/DX = 0.0 !
! A2 L(2,1,3,-3,-2) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
A force value close to zero demonstrated that the lowest potential energy has been achieved and the structure has been optimized. The bond length calculated, 1.1691 Å, is also close to the literature value, 1.168 Å.[2]
Vibration Analysis
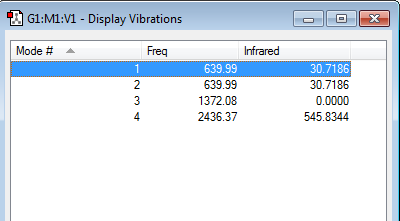
Carbon dioxide is a linear molecule, hence 3N-5 rule is applicable. Hence, 4 different mode of vibration is expected. However, in experimental spectrum, only 2 bands would be expected. MODE 1 and 2 are bending vibration, which are degenerated in energy. MODE 3 (in the above figure) is symmetrical stretching vibration, which lead to no change in the dipole moment of the molecule and doesn't lead to absorption of IR light. Mode 4 is asymmetrical stretching vibration and leads to the greatest change in dipole moment. The band in spectrum for this mode should have the greatest absorption intensity.
Charge Analysis
Overall, this molecule is neutral. Carbon is less electronegative than oxygen. Therefore, it is expected that oxygen would have a partial negative charge and carbon would have a partial positive charge. The sum of the charge of the three atoms in the molecule should be zero.
calculation result

Carbon: 1.022
Oxygen 1: -0.511
Oxygen 2: -0.511
