Rep:Mod:CC0987
Introduction
Computational Chemistry serves as an important tool for chemists to analysis structures and bondings of different molecules, thus projecting the reactivity of a particular reaction. The following wiki-page demonstrated the analysis results of NH3, H2, N2 and SiH4, where the molecules are optimised in the following set-up:
Method: B3LYP Basis Set: 6-31G(d,p)
The structure, energy and vibration modes analysis of the molecules allow us to draw conclusion on the reactivity of the reaction of N2 + 3H2 -> 2NH3.
Cheletropic MO |
NH3
Molecule Name: Ammonia (NH3)
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy, E(RB3LYP): -56.55776873 a.u.
RMS Gradient Norm: 0.00000485
Point Group: C3V
N-H Bond Length: 1.01798 Å (angstrom)
This agrees with the literature value of 1.02 Å. [1]
H-N-H Angle: 105.741o
Ammonia |
The optimisation file is linked to here
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
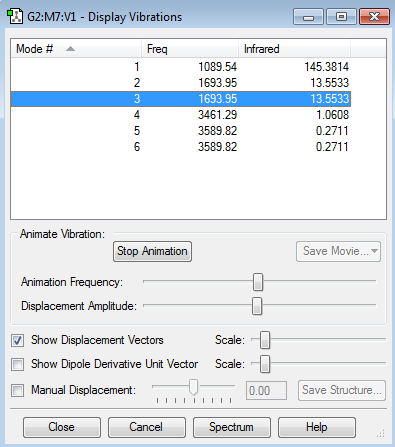
Vibration Modes and Analysis
1. There are 6 vibration modes from the 3N-6 rule for non-linear molecule
2. With mode 2 and 3 being degenerate at frequency of 1693.95 cm-1, and mode 5 and 6 being degenerate as well at frequency of 3589.82 cm-1.
3. Out of the six modes, modes 1,2 and 3 are bending and the other three are bond stretching.
4. Mode 1 at frequency of 1089.54 cm-1 and mode 4 at frequency at 3461.29 cm-1 are highly symmetrical.
5. Mode 1 has an umbrella vibration mode at frequency of 1089.54 cm-1.
6. There could be 4 possible bands in an Infrared (IR) spectrum, but only 2 are expected to be observable.
Mode 1: Observable at 1089.54 cm-1 with noticably high intensity of 145.3814
Mode 2 and 3: These 2 modes are degenerate so they will combine to give one peak at 1693.95 cm-1 with an intensity of 27.1066
Mode 4: This mode has such low intensity of 1.0608 that makes it not noticable
Mode 5 and 6: These 2 modes are degenerate and intensity will be doubled, however, the intensity of peak (i.e. 0.5422) is still too low to be observable.
Out of the six modes only the bending vibrations have high enough intensities to be observable on the IR spectrum. This is because bending causes shape of NH3 to change greatly giving a greater change in dipole moment, whereas, bond stretching generate a relatively subtle change in dipole moment of the molecule.
Charge on N-atom: -1.125
Charge on H-atom: 0.375
There is a negative charge on N-atom be cause it is more electronegative than hydrogen, thus giving it a negative charge value. This agrees with the literature electronegativity values of H (i.e. 2.20) which is smaller than that of N (i.e. 3.04)[2]
H2
Molecule Name: Hydrogen (H2)
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy, E(RB3LYP): -1.17853936 a.u.
RMS Gradient Norm: 0.00000017
Point Group: D*H
H-H Bond Length: 0.74279 Å (angstrom)
This agrees with the literature value of 0.74 Å. [1]
Hydrogen |
The optimisation file is linked to here
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Frequency: 4465.68 cm-1
Since H2 is linear and the bond vibration does not contribute to a change in dipole moment, therefore no peak will be observable in a spectrum of hydrogen.
N2
Molecule Name: Nitrogen (N2)
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy, E(RB3LYP): -109.52412868 a.u.
RMS Gradient Norm: 0.00000060
Point Group: D*H
N-N Bond Length: 1.10550 Å (angstrom)
This bond length agrees with the literature value of a N-N triple bond (i.e. 1.13 Å). [1]
Nitrogen |
The optimisation file is linked to here
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Frequency: 2457.33 cm-1
Similar as H2, N2 is linear and there is no change in dipole moment caused by bond vibration, therefore no peak will be observable in a spectrum of nitrogen.
Reaction Energy Calculations
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.11553746 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -146.48 kJmol-1
Since the enthalpy change of the reaction is negative, therefore the reaction is exothermic and ammonia product is more stable than that of gaseous reactants.
My Choice of Molecule: SiH4
Molecule Name: Silane (SiH4)
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy, E(RB3LYP): -291.88802760 a.u.
RMS Gradient Norm: 0.00000002 a.u.
Point Group: TD
Si-H Bond Length: 1.48485 Å (angstrom)
H-Si-H Angle: 109.471o
SiH |
The optimisation file is linked to here
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Charge on Si-atom: 0.629
Charge on H-atom: -0.157
H has a negative charge, showing that hydrogen is more electronegative than silicon, thus electrons are more attracted towards H atoms. This agrees with the literature electronegativity value of H (i.e. 2.20) and Si (i.e. 1.90), value of H being greater than Si. [2]
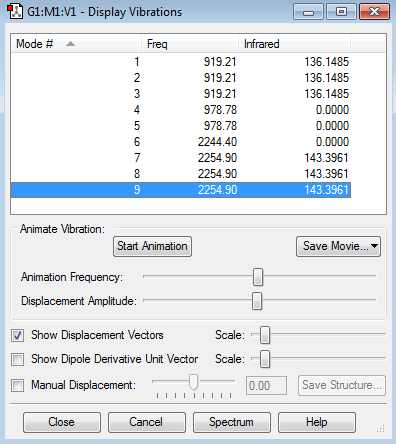
Vibration Modes and Analysis
1. There are 6 vibration modes from the 3N-6 rule for non-linear molecule.
2. Mode 1, 2 and 3 are degenerate at frequency of 919.21 cm-1. Mode 4 and 5 are also degenerate with a frequency of 978.78 cm-1, but these vibrations do not cause a change in dipole moment. Lastly, mode 7, 8 and 9 are degenerate as well at 2254.90 cm-1.
3. Out of the nine modes, modes 1 to 5 are bending and the other four modes are bond stretching.
4. Mode 4 and 5 at frequency of 978.78 cm-1, mode 6 at frequency at 2244.40 cm-1 and mode 9 at 2254.90 cm-1 are highly symmetrical vibrations.
5. Only 2 peaks in an IR spectrum of SiH4 are expected to be observable.
Mode 1-3: These three modes are degenerate so they combine together to give one peak at 919.21 cm-1 with intensity of 408.4455.
Mode 4-5: Although these two vibrations are bending, but since the change in dipole moment caused by individual bond bending of the molecule cancels out each other, there is not net change in dipole moment of the molecule as a whole. Therefore, these vibration modes will not contribute to a peak in the spectrum.
Mode 6: Similar as mode 4 and 5, it does not cause a net change in dipole moment of the molecule, so it does not cause a peak in the spectrum.
Mode 7-9: These modes are degenerate with equal intensities. The peak caused by these vibrations will have triple intensities of 430.1883 at frequency 2254.90 cm-1.
Orbitals Analysis
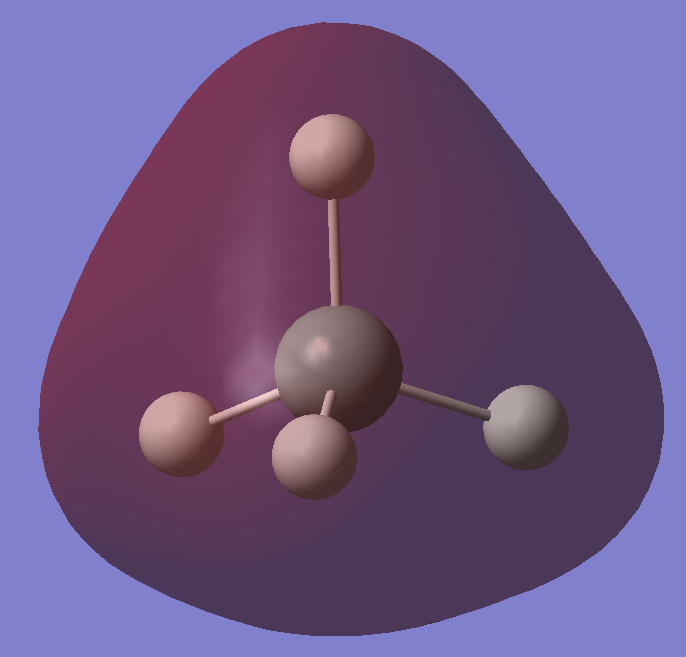
1s orbital of Si which is hidden inside the atom. It has the lowest energy of all orbitals and electrons in this orbitals are localised, thus it does not form bond with the hydrogen.
2s orbital of Si, it is non-bonding as well due to similar reasons as the 1s orbital. The electrons in this orbital have low energies and are localised, hence it is not favourable for bonds to form with electrons in this orbital.
2p orbitals of Si, it has other 2 degenerate orbitals with same energy and they are all non-bonding due to their low energies. Also, they are not diffused enough for it to overlap with the hydrogen 1s orbital, so they remain non-bonding.
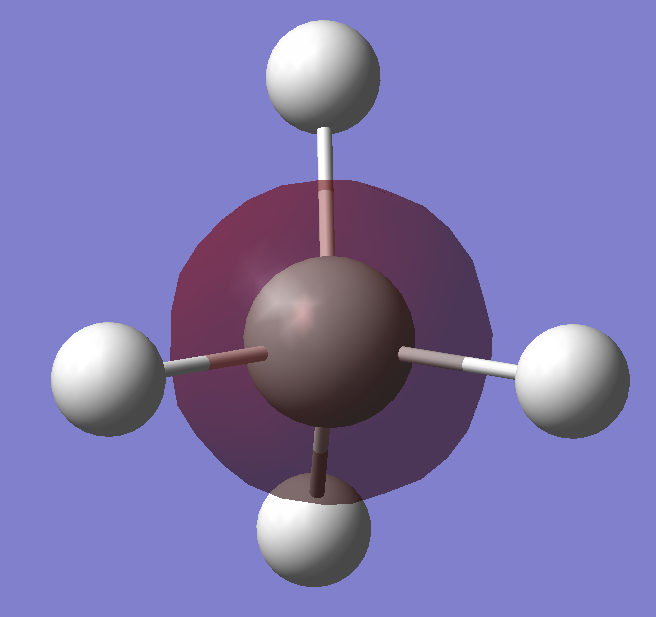
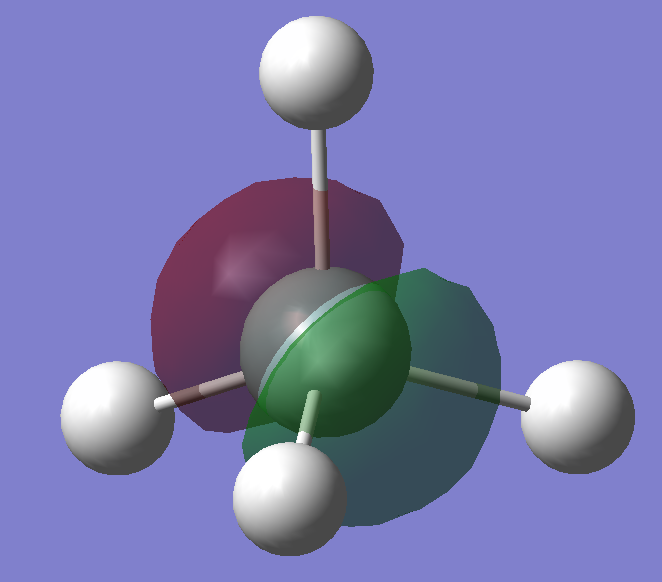
3s orbital of Silicon bonding with the 1s orbitals of the hydrogens. The bonding occur as the 3s orbitals are diffused, allowing the 3s and 1s orbtials to overlap and forming a bond. Also, it has higher energy than electrons in inner orbitals, which makes this bond formation favourable.
The anti-bonding orbital of the 3s-1s bonding orbital
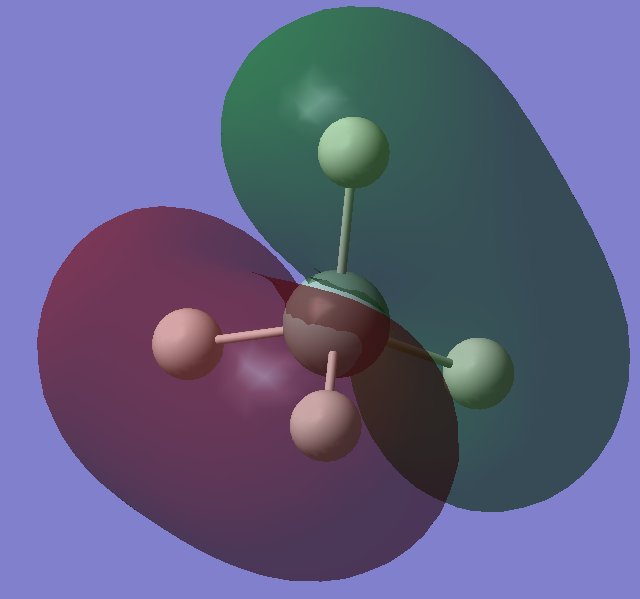
The 3p orbital of silicon bonding with the s orbitals of the hydrogen atoms. There are 3 degenerate orbitals at same energy in total and they are all HOMOs (highest occupied molecular orbitals). These orbitals are diffused with the highest enegies, so it has greater overlapping surface with hydrogen 1s orbitals. Hence, bonds are formed.
Anti-bonding orbitals of the bonding between 3p orbital of silicon and the s orbital of hydrogen. It has 2 other degenerate orbitals, like its bonding orbitals, and they are all LUMOs (lowest unoccupied molecular orbitals).
Reference and Bibliography
[1] CRC Handbook of Chemistry and Physics, 94th ed. http://www.hbcpnetbase.com. Page 9-48. Retrieved 18 June 2013.
[2] CRC Handbook of Chemistry and Physics, 94th ed. http://www.hbcpnetbase.com. Page 9-97. Retrieved 18 June 2013.
Computational Chemistry Lab - Molecular Modelling 2ː
http://www.huntresearchgroup.org.uk/teaching/year1_lab_start.html