Jump to content

Rep:Mod:CAI1234

From ChemWiki

NH3

Optimisation Data

An optimisation was run on an NH3 molecule, using the calculation method RB3LYP and basis set 6-31G(d,p). The final energy was found to be -56.55776873 a.u., the RMS gradient was 0.00000485 a.u. and the point group was C3V. The N-H bond distance was optimized at 1.01798 a.u. and the H-N-H bond angle was optimised at 105.741o. Literature values quote the bond length as 1.012A, and the bond angle as 106.7o[1]. There is a slight discrepancy between both the calculated N-H bond distance and H-N-H bond angle with the experimental literature values, suggesting the computational calculations are not ideal for this molecule. However, overall the error in both is less than 1%, which is a relatively successful prediction.

NH3 molecule

The 'item' table from the results of the optimisation is presented below, showing the force and displacement have both been converged and the optimisation was completed correctly. 

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
 Predicted change in Energy=-5.986267D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.018          -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.018          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.018          -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              105.7412         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              105.7412         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              105.7412         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)           -111.8571         -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

The full log file is available below:

Media:CAI_NH3_OPTIMISE_text.LOG

Vibrational Modes

NH3 Vibrational Modes

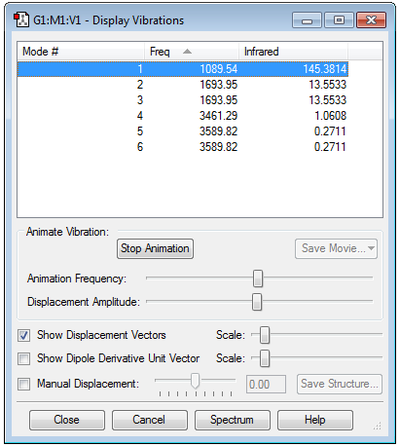
As ammonia contains four atoms and is a non-linear molecule, it is predicted that there will be 6 degrees of freedom: 3N-6=3(4)-6=6 degrees of freedom, and thus 6 vibrational modes are expected.

The generated vibrations show two sets of degenerate vibrational modes (i.e. of the same frequency) - modes 2 and 3, and modes 5 and 6.

Vibrational modes 1, 2 and 3 show N-H bond bending, and vibrational modes 4, 5 and 6 show N-H bond stretching. As expected, the stretching frequencies are higher than the bending frequencies.

Vibrational mode 4 is highly symmetric, and vibrational mode 1 is the umbrella mode.

4 bands are expected in the experimental spectrum.

Charge Distribution

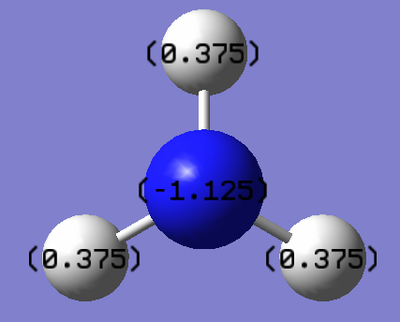
The charge on the nitrogen atom is found to be -1.125eV and the charge on the hydrogen atoms is found to be +0.375eV. A slightly polar covalent bond is expected in ammonia, due to the differing electronegativities of nitrogen and hydrogen. Nitrogen has an electronegativity of 3.04, whilst hydrogen has an electronegativity of 2.20[2] on the Pauling scale. Due to the greater electronegativity of nitrogen, this atom is expected to pull electron density towards itself, leading to a slight negative charge on the nitrogen atom, and an evenly split positive charge across hydrogen (as each hydrogen atom is in the same environment).

NH3 Charges

H2

Optimisation Data

An optimisation was run on an H2 molecule, using the calculation method RB3LYP and basis set 6-31G(d,p). The final energy was found to be -1.17853936 a.u., the RMS gradient was 0.00000017 a.u. and the point group was D*H. The H-H bond distance was optimized at 0.74279 a.u. and the H-H bond angle is 180o, as expected for a homonuclear diatomic molecule. Literature values quote the bond length as 0.74A[3], and thus the computed value is coherent with the literature value.

H2 molecule

The 'item' table from the results of the optimisation is presented below, showing the force and displacement have both been converged and the optimisation was completed correctly. 

         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
 Predicted change in Energy=-1.164080D-13
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  0.7428         -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

The full log file is available below:

Media:CAI_H2_OPTIMISE.LOG

Vibrational Modes

H2 Vibrational Modes

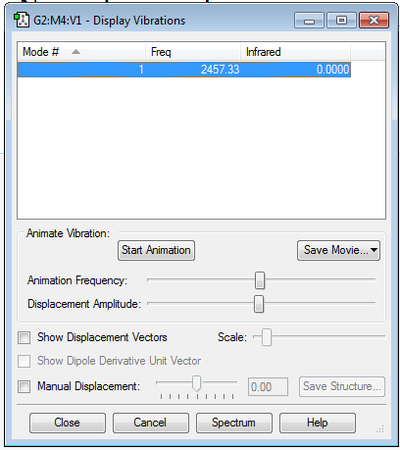
As H2 is a homonuclear diatomic molecule and thus is linear, it is predicted that there will be 1 degree of freedom: 3N-5=3(2)-5=1 vibrational mode, which is the result using GaussView. This vibrational mode is due to the H-H bond stretch.

N2

Optimisation Data

An optimisation was run on an N2 molecule, using the calculation method RB3LYP and basis set 6-31G(d,p). The final energy was found to be -109.52412868 a.u., the RMS gradient was 0.00000060 a.u. and the point group was D*H. The H-H bond distance was optimized at 1.10550 a.u. and the H-H bond angle is 180o, as expected for a homonuclear diatomic molecule. Literature values quote the bond length as 1.10A[3], and thus the computed value is coherent with the literature value.

N2 molecule
         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES
 Predicted change in Energy=-3.401052D-13
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1055         -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

The full log file is available below:

Media:CAI_N2_OPTIMISE.LOG

Vibrational Modes

N2 Vibrational Modes

As with H2, N2 is a homonuclear diatomic molecule and thus is linear, it is predicted that there will be 1 degree of freedom: 3N-5=3(2)-5=1 vibrational mode, which is the result using GaussView. This vibrational mode is due to the H-H bond stretch.

Haber-Bosch Energy Calculation

The energies that have been calculated for H2, N2 and NH3 can be used to calculate a value for the energy change of the Haber-Bosch process.

3*H2 + N2 --> 2*NH3

E(NH3)=-56.55776873 a.u.

2*E(NH3)=-113.11553746 a.u.

E(N2)=-109.52412868 a.u.

E(H2)=-1.17853936 a.u.

3*E(H2)=-3.53561808 a.u.

ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.0557907 a.u.

ΔE=2625.5*(-0.0557907)=-146.4784829 kJ.mol-1

The process is exothermic, and thus the products are more stable (deeper in energy) than the reactants.

The literature value for the enthalpy change of the Haber process is quoted as -91.8 kJ.mol-1[4], which is considerably lower than the computed value. The computational model has clearly failed here.

H2SiO

Optimisation Data

An optimisation was run on an H2SiO molecule, using the calculation method RB3LYP and basis set 6-31G(d,p). The final energy was found to be -365.90001403 a.u., the RMS gradient was 0.00000941 a.u. and the point group was CS. The Si=O bond distance was optimized at 1.53172 a.u. and the Si-H bond distance was optimized at 1.48652 a.u.. The O-Si-H bond angle was optimised at 124.156o, and the H-Si-H bond angle was optimised at 111.686o.

HSiO molecule
         Item               Value     Threshold  Converged?
 Maximum Force            0.000023     0.000450     YES
 RMS     Force            0.000009     0.000300     YES
 Maximum Displacement     0.000023     0.001800     YES
 RMS     Displacement     0.000017     0.001200     YES
 Predicted change in Energy=-5.109774D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.4865         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.4865         -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.5317         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              111.686          -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              124.1565         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              124.1576         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

The full log file is available below:

Media:CAI_H2SIO_OPTIMISE.LOG

Vibrational Modes

H2SiO Vibrational Modes

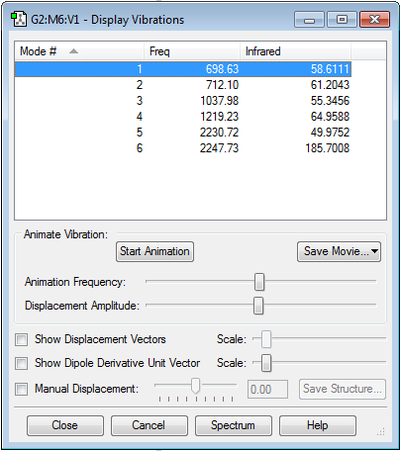
As H2SiO contains four atoms and is a non-linear molecule, it is predicted that there will be 6 degrees of freedom: 3N-6=3(4)-6=6 degrees of freedom, and thus 6 vibrational modes are expected.

The generated vibrations show no degenerate vibrational modes (i.e. of the same frequency).

Vibrational modes 1 and 2 show Si-H bond bending.

Vibrational modes 3 and 4 show bending of the Si-H bonds and stretching on the Si=O bond.

Vibrational modes 5 and 6 show Si-H bond stretching - with vibrational mode 5 showing a symmetric stretch and vibrational mode 6 showing an asymmetric stretch.

6 bands are expected in the experimental spectrum.

Charge Distributions

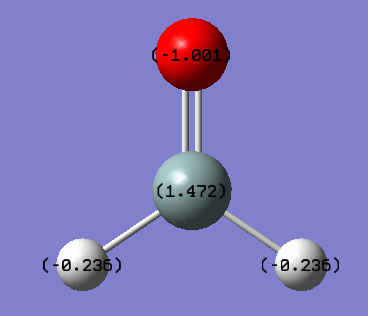
The charge on silicon was found to be +1.472 eV, the charge on oxygen was found to be -1.001 eV and the charge on hydrogen was found to be -0.236 eV. This follows the electronegativity difference between the elements. Silicon has the lowest electronegativity of 1.90[2] and thus attracts the electron density the least, leading to a positive charge on the silicon atom. Oxygen has the highest electronegativity of 3.44[2], and thus has the greatest negative charge as this atom attracts the electron density the most. Hydrogen has a slightly greater electronegativity than silicon at 2.20[2], and thus is slightly negatively charged with respect to the silicon.

H2SiO Charge Distribution

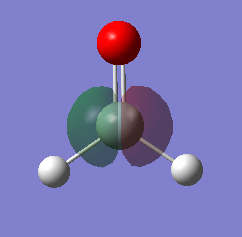
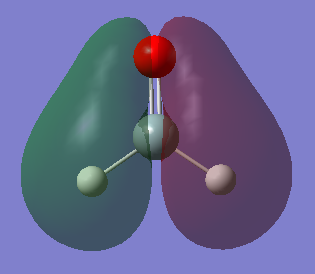
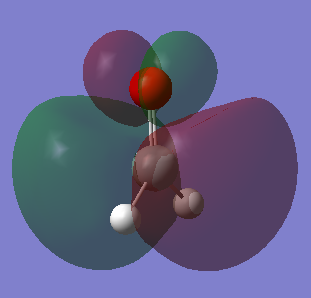
Molecular Orbitals

Five of the H2SiO molecular orbitals are analyzed below:

This molecular orbital shows one of the three degenerate Si 2p orbitals. This orbital is non-bonding as it is too deep in energy to be involved in bonding (-3.68178eV). The two other p orbitals have very similar energies, but not quite identical (-3.68923eV and -3.68220eV). The orbital is occupied by two electrons.
This molecular orbital shows an Si-O sigma bond. This is a bonding orbital and is occupied by two electrons. This orbital is much higher in energy than the 2p orbital, and has an energy of -0.92465eV. The electron density is centred around the oxygen atom, as the 2p-3p overlap leads to the molecular orbital being closer in energy to the oxygen atom, and the greater electron density on the oxygen atom.
This molecular orbital is an anti-bonding orbital with a node across the Si-O plane and electron-density centred around the H atoms. The orbital is occupied by two electrons and is higher in energy than the Si-O sigma orbital, with an energy of -0.39697eV.
This is the highest occupied molecular orbital, clearly showing some partial d-character - as expected with the low-energy d-orbitals on silicon. The HOMO is (by definition) occupied, with two electrons, and is the highest energy occupied orbital, with an energy of -0.28497eV. Electron density is centred away from the central Si atom, suggesting an anti-bonding orbital.
This is the lowest unoccupied molecular orbital, centred on the Si and O atoms. The orbital again shows some d-character, and is the highest energy orbital, with an energy of -0.07728eV. This is an anti-bonding orbital, as there is a node along the Si-O plane.

References

1: Ammonia Data Page, Wikipedia, retrieved 10/03/17, https://en.wikipedia.org/wiki/Ammonia_(data_page)

2: List of Electronegativity Values of the Elements, Science Notes, retrieved 10/03/17, http://sciencenotes.org/list-of-electronegativity-values-of-the-elements/

3: Common Bond Energies and Bond Lengths, Wired Chemist (Yoder, 2017), retrieved 10/03/17, http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html

4: Haber Process, Wikipedia, retrieved 10/03/17, https://en.wikipedia.org/wiki/Haber_process

Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:CAI1234&oldid=816413"