Rep:Mod:CAB14MgO

Abstract

The quasi-harmonic approximation (QH) and molecular dynamics (MD) methods were used to determine the volumetric thermal expansion coefficient of MgO. The two methods were chosen to compare their accuracy at different temperatures. Cells were optimised from 0-1000 K and their volumes recorded. Between 400 K - 800 K, both methods showed good agreement but above 800 K the MD method underestimated the cell size due to the supercell used not accounting for the high velocity electrons. No quantum correction was considered which meant that the simulation underestimated the crystal volume in below 400 K. QH (2.6544 x 10^-5 K^-1 for 400-1000 K) and MD (3.019192 x 10^-5K^-1for 100-1000 K) overestimated the experimental expansion coefficient but the trends from QHA agreed the literature better than MD in the temperature range investigated.

Introduction

The thermal expansion coefficient is an intrinsic property of a crystals that can be calculated using either quasi harmonic or molecular dynamic methods. Equation 1 shows the equation for thermal expansion where V0 is the volume of the crystal at 0 K. The quasi harmonic method involves the use of quantum theory, with thermal expansion being calculated from the phonon dispersion and vibrational density of states. Molecular dynamics simulates the vibration of a crystal as the random motions of the atoms within a cell, using Newtonian mechanics to calculate the parameters of the cell.

$\alpha =\frac{1}{V_0}{\left(\frac{\partial V}{\partial T}\right)}_P\text{(Equation 1)}$

Both methods involve modelling MgO as a uniform crystal with a face centred cubic lattice, as shown in Figure 1 with the primitive cell as a perfect cube $(a=b=c\alpha =\beta =\gamma =90^{\circ })$. The conventional cell (2x2 of the primitive cell) contains 8 atoms as shown in Figure 2. The lattice parameter is taken to be the length of one side of the unit cell, and is equal to the distance between 2 of the same type of atom.

Figure 1 - The MgO Primitive Cell

Figure 2 - The MgO Conventional Cell

The two methods were chosen to compare their accuracy at different temperatures when compared to literature values. Computational methods allow the crystal to be accurately investigated with DOS and Phonon dispersions being calculated to give extra information about the crystal structure and properties.

Quasi–Harmonic Theory

These calculations occur in reciprocal space, the Fourier transform or real space, with each atom coordinate within the cell being transformed by Equation 2, where a,b and c represent the lattice vectors in real space, and a* represents a in reciprocal space.

${\mathbf{a}}^{\mathbf{*}}=\frac{2\pi \mathbf{b}\times \mathbf{c}}{\mathbf{a}\cdot \mathbf{b}\times \mathbf{c}}\text{(Equation 2)}$

The vibrations of each molecule can be described using the notation of the electronic state. Discrete vibrational states, known as phonons, can be described using a parameter k known as the crystal wave vector. k is defined by the Bloch function in Equation 3, where r is position, is the Bloch wave and u is a periodic function with the same periodicity as the crystal being examined. k can be used to describe vibrations as this is equivalent to positive and negative interactions of molecules.

$\psi (\mathbf{r})={\mathbf{e}}^{ik\cdot \mathbf{r}}u(\mathbf{r})\text{(Equation 3)}$

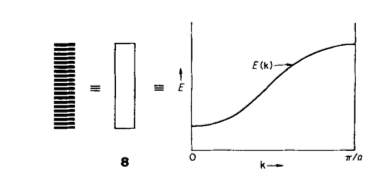
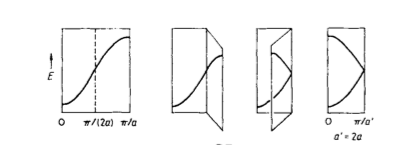
If you imagine each dimension of the crystal is a 1d line of atoms, each with an associated AO then the number of MO’s of the system is equal to the number of atoms within the system. As the number of atoms increase, the number of MO’s increases until eventually the energy gap between each energy level is smaller than kBT, creating a continuous energy band, as shown in Figure 3. The molecular orbitals for each cell are described using Equation 4 (where represents the AO of your selected basis set), with varying k values along the energy band causing energy to change. Figure 3 shows the conversion of this energy band to a plot of E(k) vs k. The band runs between $\frac{\pi }{2}$ and $-\frac{\pi }{2}$ with $\gamma$, the lattice symmetry point (0,0,0) being used as an origin. The orientation of the basis set of molecules determine the shape of the band.

${\psi }_k=\sum _m{e}^{ikna}{\chi }_{\alpha }\text{(Equation 4)}$

Figure 3 - MO conversion to energy band gap

This band, the dispersion band, can then be used to calculate the DOS of a system, as shown in Figure 4 . The Density of States is the number of vibrational states per frequency interval.

Figure 4 - Comparison of the dispersion band and DOS for MoS

To increase the accuracy of the phonon dispersion and DOS for large crystals, a larger range of k numbers are measured, with new points adding in between the old ones. A larger grid size in real space, means a smaller cell in reciprocal space as shown in derivation. As the cell size decreases, so does the range of the energy dispersion, with the energy band reflected along the ‘fold’ as shown for an increasing cell size from 1 to 2 in Figure 5 . This causes a more complex phonon dispersion and therefore DOS as grid size is increased, which diverges towards a true representation of the cell.

Figure 5 - DOS variation with cell size

The free energy of the cell can be calculated using Equation 5, where F is free energy, E₀ is internal lattice energy and is bond frequency. Increasing grid size increases the number of vibrations within the calculation and this will eventually cause the free energy to converge.

In this theory, the free energy of the cell is minimized and this occurs by finding the equilibrium cell at each temperature.

$F=E_0+\frac{1}{2}\sum \overline{h}{\omega }_{j,k}+k_{B}T\sum \ln [1-e^{\frac{\overline{h}{\omega }_{j,k}}{k_{B}T}}]\text{(Equation 5)}$

This method of calculation is known as quasi- harmonic, as the harmonic approximation doesn’t account for increased volume and therefore can’t be used to explain thermal expansion. Figure 6 shows a Lennard-Jones potential with a parabola at equilibrium representing the harmonic approximation. As temperature increases the equilibrium bond length is constant, therefore no change in volume can occur. To account for the thermal expansion it is treated as anharmonic and the bonds within the crystal as harmonic, meaning they can never break even at infinite temperatures, this is shown graphically in Figure 7.

The cause of the thermal expansion within this model is due to Badger’s rule , which describes that as a bond length increases the force constant and therefore ω decreases. At low temperatures the first two terms dominate the free energy equation, therefore the expansion is driven by reduction of $\omega$ leading to a lower zero-point energy and overall a more negative free energy. At high temperatures the third term of the equation becomes more significant, and provides an additional decrease in F as $\omega$ decreases.

In this method, calculations were initially run at 300 K to find the phonon dispersion. The grid size was then varied and the DOS calculated to optimise the number of k points used. Finally the cell volume and lattice parameters were calculated at varying temperatures between 0 and 1000 K, to model the thermal expansion of the crystal, by optimising the cell structure at each temperature.

Figure 6 - Harmonic Lennard-Jones potential

Figure 7 - Quasi-Harmonic Lennard-Jones potential

Molecular reaction dynamics

Molecular reaction dynamics uses Newtonian Mechanics (F=ma), to model the motion of atoms, with time averages of their behaviour being used to compute the crystal properties. Molecular dynamics uses a supercell with 64 atoms to accurately and efficiently model the random motion of molecules, this is 2x2x2 the conventional cell. The supercell is used as running the calculations on a single cell would be equivalent of every cell in the crystal moving perfectly in phase, which is equivalent to only sampling one k point and is not physically accurate.

Increased kinetic energy on heating is the physical reason for thermal expansion. Molecules have increased vibrational motion and therefore have an increased average distance, leading to an overall increase in unit cell, and therefore crystal volume.

In this method, the supercell volume was calculated at temperatures between 0 and 1000 k, using an NPT ensemble. The system had a time step of one femtosecond and ran for 500 steps after the equilibrium cell was reached. At each temperature, the average equilibrium cell volume was recorded and then used to calculate the thermal expansion coefficient of MgO.

Results and Discussion

Figure 8 - DOS for a 1x1x1 Grid Size

Figure 9 - DOS for a 2x2x2 Grid Size

Figure 10 - DOS for a 4x4x4 Grid Size

Figure 11 - DOS for a 8x8x8 Grid Size

Figure 12 - DOS for a 16x16x16 Grid Size

Figure 13 - DOS for a 32x32x32 Grid Size

Figure 14 - DOS for a 64x64x64 Grid Size

Figure 15 - Phonon Dispersion of MgO

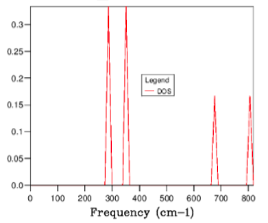
Figures 8-14 show the phonon DOS for varying grid size between 1x1x1 and 64x64x64. The first phonon DOS, Figure 8, represents the L symmetry point, as can be seen from a comparison with the phonon dispersion, Figure 15. The output data shows the first phonon DOS has two double degenerate states at 286 cm^-1 and 351 ^-1, and two non- degenerate states at 667^-1 and 806^-1 , which are comparable with the approximate values from the phonon dispersion.

From the results in figures 8 to 14 it can be concluded that as the grid size is increased the DOS becomes more defined and smoother, showing more detailed peaks, thus approaching the crystals true DOS. As the grid size tends to infinity the DOS curve would perfectly represent the crystal, however due to time constraints it is not physically possible to complete this calculation.

The DOS curves for a grid size of 32x32x32 and 64x64x64 , Figures 13 and 14 are almost identical, as the DOS converges to the true value. Therefore the 32x32x32 grid size was taken to be the optimal grid size, being the smallest size to show a reasonable approximation for the DOS, allowing for fast but accurate calculations to be run. When compared to smaller grid sizes, such as 16x16x16 (Figure 12), it can be seen that the smaller grid size leads to a significantly less smooth and therefore less representative DOS curve due to the smaller number of wave frequencies measured.

This grid size would be suitable for a crystal with a similar lattice parameter to MgO such as CaO, which has a lattice parameter of 4.804 Å compared to 4.211 Å . For a Zeolite such as Faujasite which has a much larger lattice parameter of 24.638 Å in reciprocal space a smaller grid would be required to get an accurate representation of the DOS. For a metal, when modelled with covalent bonds these bonds would be extremely short and therefore in reciprocal space a large grid size would be required to model the crystal accurately.

Figure 16 shows the plot of free energy vs grid size. The free energy of the crystal can be described using equation 5 in the quasi harmonic approximation. Table 1 shows the free energy at every grid size, as well as the difference in energy for each grid size from the 64x64x64.

Figure 16 - QH Free Energy vs Grid Size

Figure 17 - QH Free Energy vs Temperature

Table 1 - QH Free Energy Data

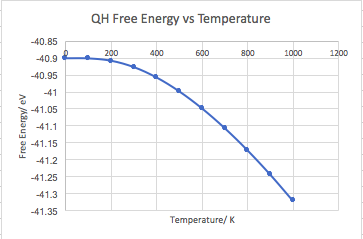
Figure 17 shows the plot of free energy vs temperature for a 32x32x32 grid size. The initial section of this graph is described by the first two terms of Equation 5, meaning it is almost constant. As temperature increases, the third term becomes more significant and the thermal expansion becomes linear.

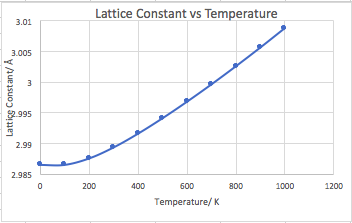
The graph of lattice constant vs temperature, Figure 18, also shows the lattice constant increasing with temperature, as expected due to the thermal expansion of the MgO cell and Badgers rule.

Figure 18 - QH Lattice Constant vs Temperature

Figure 19 - QH Cell Volume vs Temperature

The thermal expansion coefficient was calculated as 2.6544 x 10^-5 K ^-1, from the gradient of figure 19 between 400 and 1000 K, using Equation 1. The literature value for expansion coefficient is 1.140x10-5 K^-1 (120 - 270), which is slightly lower than calculated. A potential cause for this is the QH assumption that the crystal lattice was perfect with no defects and the periodic boundary conditions meant the lattice was modelled as infinite.

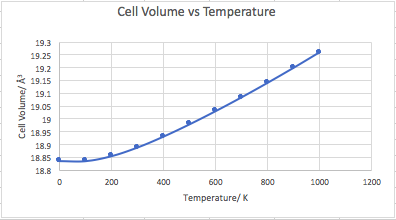
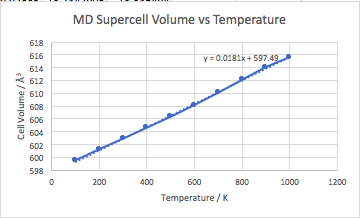
Figure 20 shows the cell volume vs temperature for MD. No value was calculated for 0 K as using this method as the crystal approaches 0k the cell approaches a volume of 0 ų. This is not physically accurate and is accounted for by the zero point motions in the quasi harmonic model, leading to a non-zero cell volume at 0 K. The thermal expansion coefficient was calculated as 3.019192 x 10^-5K^-1 (100-1000 K) for MD and it is slightly higher than the lit value of 1.140x10^-5K^-1 (120 - 270K) , due to fundamental flaws in these calculations such as not accounting for any quantum phenomena.

Figure 20 - MD Supercell Volume vs Temperature

Figure 21 - A comparison of Cell Volume vs Temperature

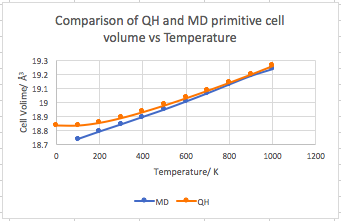
Figure 21 shows the cell volume vs temperature for both the quasi- harmonic and the molecular dynamic methods. The methods converge to the same value as temperature increases. The values for molecular dynamics are always slightly lower below this temperature as no quantum effects are accounted for by this method. Above 800 K the quantum effects of the zero point energy becomes insignificant and the two methods should converge. However in this case the MD volume decreases above 800 K, which is caused by the supercell being too small. The cell size means that the simulation couldn’t model the atoms with the greatest velocity, as they travel a distance larger than that of the supercell.

As temperature tends to infinity the cell volumes could theoretically increase forever, but the crystal could never melt and this is an example of both methods breaking down. For a crystal to melt a phonon must be resonant with the molecular sheets at the surface of the structure but the assumptions of the model mean a bond can never break, only extend to an infinite length.

Conclusion

Both the QH (2.6544 x 10^-5 for 400-1000 K) and MD (3.019192 x 10^-5 for 100-1000 K) methods were both successfully used to calculated the thermal expansion coefficient, to varying degrees of accuracy. The MD method breaks down at low temperatures as it doesn't account for quantum effects, therefore predicting a cell volume of 0 at 0 K, and is not accurate at large temperatures due to a small supercell size. QH methods are more accurate but due to the assumption of a perfect crystal lattice they overestimate the thermal expansion coefficient in comparison with the lit value 1.140x10^-5K^-1 (120 - 270K).