Rep:Mod:C1

Year 3 Synthetic Modelling Lab by Jan Szopinski. Please do not edit this page.

Conformational analysis using Molecular Mechanics

Molecular Mechanics

Molecular mechanics is a computational method that avoids solving quantum mechanical equations by treating the atomic interactions in a classical manner. In its simplest form, potential energy of a molecule is calculated as a sum of bonded (stretches, bends, torsions) and non-bonded (van der Waals and electrostatic) interactions. Various force fields have been devised to provide the method with empirical parameters. While molecular mechanics are very fast and suitable for large systems, there is a tradeoff for accuracy. A force field suitable for this experiment is MMFF94s, which is well parametrised for typical organic molecules, as implemented in Avogadro. When molecular mechanics methods are used to optimise molecule structure, they can lead to false minima, artifacts of the simplified classical treatment. Therefore, whenever the system size allows, the structure should be verified at least with a low-level ab-initio method. An advantage of the simplified treatment, however, is that the calculated energies can be broken down into components, indicating how steric strain or electrostatic interactions differ between isomers.

The Hydrogenation of Cyclopentadiene Dimer

Fig.1 Structures of cyclopentadiene dimer (exo and endo) and the possible dihydro derivatives of the endo form.

Dimerisation of cyclopentadiene

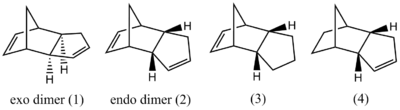
Cyclopentadiene spontaneously dimerises at room temperature in a Diels-Alder reaction. This reaction proceeds exclusively to give the endo product (2 on Fig.1). Molecular mechanics cannot model processes of bond breaking or forming but it can be used to compare relative energies of isomers of the same connectivity. This approach can select the thermodynamically favoured product within the limited accuracy of molecular mechanics.

Hydrogenation of endo cyclopentadiene dimer

Subsequent hydrogenation of the endo dimer produces a dihydro form, and the addition of another hydrogen molecule to the remaining double bond happens at a much slower rate. Molecular mechanics can be employed to predict hydrogenation of which double bond yields a more stable product.

Modelling compounds 1-4

The structures optimised at the MM level are shown in the table together with energies broken down into components (not all shown). Two structures of compund 3 have been found, corresponding to the cyclopentane ring pointing towards and away from the rest of the molecule. The structures can be visualised by clicking on the buttons in the first column.

Compound	Structure	Total energy / (kcal/mol)	Stretching / (kcal/mol)	Bending / (kcal/mol)	Torsional / (kcal/mol)	van der Waals / (kcal/mol)	Electrostatic / (kcal/mol)
		55.374	3.543	30.772	-2.731	12.801	13.014
		58.191	3.467	33.184	-2.951	12.363	14.187
		50.723	3.309	30.863	0.059	13.282	5.121
		50.446	3.312	31.950	-1.483	13.637	5.120
		41.257	2.823	24.685	-0.378	10.637	5.147

The endo form was found to be ca. 2.8 kcal/mol higher in energy than exo. Considering that in practice the reaction yields the endo form, it must be kinetically controlled. This is indeed the case, as the transition state is well known to be stabilised by orbital interactions in the endo approach. The energy difference cannot be attributed purely to one component of the energy sum but the differences in bending (2.4 kcal/mol) and electrostatics (1.2 kcal/mol) are the major contributions favouring the exo form.

The energy difference between the two conformers of compund 3 (0.3 kcal/mol) is small compared to the amount of energy, by which formation of compund 4 is thermodynamically favoured (9.2 kcal/mol). The major components of MM energy favouring compound 4 are bending (7.3 kcal/mol) and van der Waals (3.0 kcal/mol). If the reaction is thermodynamically controlled, the major product of dihydrogenation is expected to be compund 4.

Atropisomerism in an Intermediate related to the Synthesis of Taxol

Fig.2 Two atropisomers of proposed intermediate in paclitaxel synthesis. The image was taken from the experimental script.

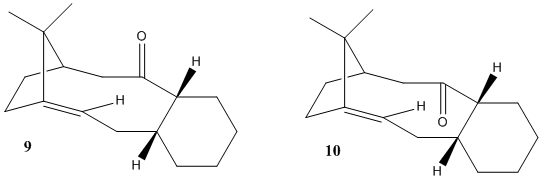
Taxol is a trademark for a naturally occuring cancer drug paclitaxel. The first total synthesis was proposed by Holton et al. The isomeric structures shown on Fig.2 contain three of the four rings in the paclitaxel molecule and have been investigated by Elmore and Paquette.. The compound can be obtained in an oxy-Cope rearrangement, which yields one of the isomers depending on other groups present in the reagent molecule. As the isomers are actually isolable conformers which arise due to restricted rotation around a single bond, they are termed atropisomers. To investigate which atropisomer is the thermodynamic product, molecular mechanics can be conveniently applied. The table sumarises energies of two conformers of each isomer.

Form	Structure	Total energy	Stretching	Bending	Torsional	van der Waals	Electrostatic
		82.714	8.188	34.110	3.773	34.711	0.210
		88.524	8.438	34.149	6.736	36.930	0.153
		60.556	7.597	18.807	0.192	33.316	-0.057
		68.893	7.777	21.379	0.919	34.505	-0.044

Clearly, the isomer with carbonyl oxygen atom pointing upwards, that is structure 10, has a significantly lower energy (by 22.2 kcal/mol). The difference is largely due to lower bending energy (15.3 kcal/mol). The thermodynamic product is therefore 10b. The structures 9b and 10b represent failed attempts to localise lower energy conformers. In both the cyclohexane ring is in a twist-boat conformation, which is normally higher in energy than a chair conformer.

Hyperstability of the Intermediates

It has been noted that compunds (9) and (10) react with hydrogen much slower than other alkenes. The class of bridhead alkenes which are inert towards hydrogenations has been termed 'hyperstable olefins'. While the double bond in the bridgehead position causes a lot of strain in cyclic molecules, it can adapt a very favourable conformation in larger polycycles. These compunds have been found to have negative olefin strain (OS) values, defined as the difference of the strain energy between the alkene and parent alkane, hence their stability. Inspecting the computed structures of compounds (17) and (18) below shows, that the double bond geometry is indeed close to that in an unstrained alkene. The reaction cannot be modelled using Molecular Mechanics as it involves bond breaking and making, however an ab-initio calculation at a modest level of theory could show the unfavourable energetics.

Spectroscopy of an intermediate related to the synthesis of Taxol

Fig.3 Dithiolane (17) isomerises to give the more stable (18). The image was taken from the experimental script.

An oxy-Cope rearrangement similar to the one described as a method of synthesis of (9) and (10) has been used to prepare its dithiolane derivative, (17) on Fig.3. This compund isomerises to give the more stable form, (18), when heated under reflux in THF over the period of five days. This pair of compunds are again atropisomers.

Molecular mechanics and ab-intio calculations

The structures were optimized with Molecular Mechanics, their energies calculated and submitted for subsequent Density Functional Theory calculations at the B3LYP level of theory and 6-31G(d,p) basis set. The energy minima were confirmed by the lack of imaginary frequencies. The energies calculated for both structures are presented in the table below. Structures can be viewed by clicking the buttons in the first column.

Molecule	Structure	Molecular Mechanics	B3LYP/6-31G(d,p)
		Total energy / (kcal/mol)	Electronic energy / (kcal/mol)	Free energy / (kcal/mol)
		100.439	-1036558.08	-1036294.574
		118.024	-1036572.471	-1036308.129
energy difference / (kcal/mol)		17.6	-14.4	-13.6

The energy difference from molecular mechanics calculation suggests, that structure (17) is lower in energy than (18). If this was the case, the conversion at thermodynamic conditions (high temperature, long duration) would not take place. DFT calculations show that the energy ordering is indeed opposite and equal to 13.6 kcal/mol. The origin of the energy difference between these two atropisomers are discussed below.

Non-covalent interactions

As the molecular mechanics predicts an opposite energy ordering, it cannot be used to decompose the interactions and find those responsible for the lowering of energy of the (18) form atropisomer. Non-covalent interaction (NCI) analysis was conducted based on the electron density from DFT calculations. On the images below, attractive interactions are shown in green-blue and repulsive in orange-red. The analysis suggests that in the (18) atropisomer, in which the carbonyl oxygen points downwards, the molecule changes its conformation so that it can interact with one of the sulfur atoms. The image shows the oxygen atom as surrounded by attractive interactions from three sides, which supposedly lowers the overall energy significantly. Therefore, (17) isomerises to (18), the thermodynamic product, when heated in THF over a prolonged period of time.

Molecule 17	Molecule 18
NCI	NCI

NMR simulations

The calculations of chemical shift were performed together with the optimisation and frequency calculation on the High Performance Computing (HPC) cluster at Imperial College. The solvent was chloroform for molecule (17) and benzene for (18) for consistency with literature.

¹³C NMR

Experimental	Theoretical	Assignment	Deviation	Experimental	Theoretical	Assignment	Deviation
Molecule 17				Molecule 18
211.49	219.83	30	-8.34	218.79	211.92	30	6.87
148.72	149.34	4	-0.62	144.63	147.87	4	-3.24
120.9	117.23	8	3.67	125.33	120.13	8	5.20
74.61	93.49	28	-18.88	72.88	92.84	28	-19.96
60.53	62.53	23	-2.00	56.19	65.94	20	-9.75
51.3	58.69	20	-7.39	52.52	54.93	3	-2.41
50.94	55.09	3	-4.15	48.5	54.76	23	-6.26
45.53	53.70	6	-8.17	46.8	49.53	6	-2.73
43.28	50.74	35	-7.46	45.76	48.04	35	-2.28
40.82	49.82	5	-9.00	39.8	45.65	48	-5.85
38.73	46.18	48	-7.45	38.81	44.01	49	-5.20
36.78	46.18	31	-9.40	35.85	41.47	31	-5.62
35.47	43.74	49	-8.27	32.66	38.51	5	-5.85
30.84	36.22	32	-5.38	28.79	33.69	32	-4.90
30	31.57	18	-1.57	28.29	32.47	18	-4.18
25.56	30.45	2	-4.89	26.88	28.36	1	-1.48
25.35	26.78	1	-1.43	25.66	26.50	9	-0.84
22.21	26.18	9	-3.97	23.86	24.45	2	-0.59
21.39	25.62	36	-4.23	20.96	24.01	36	-3.05
19.83	22.74	10	-2.91	18.71	22.58	10	-3.87
Std Dev			7.18	Std Dev			6.45

The departure from experimental values is quite significant (standard deviation 6-7 ppm). This could be due to a conformation different than the global minimum being used in the calculations. The match is good enough to assign peaks to all the carbon atoms with limited certainty. The largest deviation from experimental values was shown by carbon 28 (more than 18 ppm) due to it being bound to two sulfur atoms and associated spin-orbit coupling error. Other carbon atoms bound to sulfur show average deviations from their experimental values.

¹H NMR

Experimental	Theoretical	Assignment	Experimental	Theoretical	Assignment
Molecule 17			Molecule 18
4.84 (dd, J=7.2, 4.7Hz, 1 H)	5.88	22	5.21 (m, 1 H)	5.97	22
3.40-3.10 (m, 4H)	3.71	13	3.00-2.70 (m, 6 H)	3.12	50 and 52
	3.25	52, 50 and 51		2.95	51 and 19
2.99 (dd, J=6.8, 5.2 Hz, 1 H)	3.08	53		2.89	53
2.80-1.35 (series of m, 14 H)	3.01	19		2.80	21 and 39
	2.96	29	2.70-2.35 (m, 4 H)	2.67	13
	2.89	21		2.54	12 and 29
	2.41	7		2.43	42
	2.23	43, 40 and 14	2.20-1.70 (m, 6 H)	2.31	45 and 43
	2.12	46 and 39		1.98	14 and 7
	1.98	11		1.83	44 and 11
	1.88	44 and 38	1.58 (t, J = 5.4 Hz, 1 H)	1.64	25
1.38 (s, 3 H)	1.64	45	1.50-1.20 (m, 3 H)	1.53	40, 15 and 38
	1.57	15	1.10 (s, 3 H)	1.34	41
	1.51	42		1.27	46
1.25 (s, 3 H)	1.43	37 and 41		1.21	37 and 26
1.10 (s, 3 H)	1.28	25 and 12	1.07 (s, 3 H)	0.96	17 and 24
	1.00	16	1.03 (s, 3 H)	0.90	16
	0.83	24		0.60	47
1.10 (s, 3 H)	0.75	17
	0.69	26
	0.55	47

The agreement between predicted and experimental values is rather poor. Standard deviations could not be calculated due to unresolved peaks and overlapping multiplets in the literature spectrum. The values are helpful for assigning only the more distinct peaks in the spectrum.

Chiral catalysis

Chiral Catalysts

Shi precatalyst

There is one anomeric centre in the Shi prectalyst molecule. The central sugar-like ring contains one oxygen atom and a hydroxyl group transformed into a cyclic ether. The equilibration with the other anomeric form is hindered due to the hydroxyl group being protected by the five-membered ring, which it is a part of. The bond length of the ring oxygen and anomeric carbon is 1.408Å and the bond length to the other carbon is 1.414Å. The shortening of the anomeric C-O bond is insignificant, however the bond distance between the anomeric carbon and the oxygen atom involved in the 5-membered ring, which is 1.390Å is noticably shorter. Even shorter, 1.345Å and 1.380Å, are the bonds formed by the other oxygen atoms in that small ring. These contractions could be due to the geommetry of the five-membered ring.

Jacobsen precatalyst

The phenyl rings on the both opposite sides of the manganese centre do not lie on a common plane. Although this is clearly due to the tetragonyl pyramid geommetry of the transition metal, there might also be a contribution from the close distance of tert-butyl groups on the ring. A space filling model constructed from van der Waals spheres shows that the atoms might experience some interaction. This could be confirmed with NCI analysis or Bond Critical Points calculation. It is also worth noting that one of the t-Bu groups is rotated out of the closest contact with the other group. This slight rotation (3^o change of dihedral angle with respect to the ring plane) likely changes the unfavourable H-H contact to a slightly attractive interaction with carbon atoms. To confirm this, a rigid scan of the potential energy along t-Bu group rotation could be computed and the energy differences explained in terms of overlap of Natural Bond Orbitals.

Shi catalysis transiton states

Energies

Styrene

Free energies were extracted from the precomputed transition state structures. In all cases, there are four different types of attack that will give the particular enantiomer, as shown in the table below. The energies were found relative to the lowest energy TS in the series. The Arrhenius equation in terms of free energy of activation states:

$k=A{e}^{\frac{-\mathrm{\Delta }{G}^{\ne }}{RT}}$

In a kinetically controlled reaction, the concentrations are proportional to the rate constants of formation. Hence:

$\frac{c}{c_0}=\frac{k}{k_0}=e^{\frac{-(\mathrm{\Delta }{G}^{\ne }-\mathrm{\Delta }{G}_0^{\ne })}{RT}}=e^{\frac{-\mathrm{\Delta }(\mathrm{\Delta }{G}^{\ne })}{RT}}$

Hence it is clear that to know the relative concentrations (or molarities) of products, it is not a prerequisite to know the free energy of reactants. All calculations in the below table are done with relative to the lowest energy TS, which was assigned relative concentration of 1.

attacked face prochirality	dioxirane oxygen	type of approach	calculation	structure	free energy / Hartree	relative energy / (kcal/mol)	Energy difference / (J/mol)	Relative concentration	Sum of concentrations
Re	top	endo	DOI:10.6084/m9.figshare.829523		-1303.727673	6.80	28451.2	0.0000	1.0071
		exo	DOI:10.6084/m9.figshare.829522		-1303.738503	0.00	1	1.0000
	bottom	endo	DOI:10.6084/m9.figshare.830388		-1303.724178	8.99	37614.16	0.0000
		exo	DOI:10.6084/m9.figshare.828552		-1303.733828	2.93	12259.12	0.0071
Si	top	endo	DOI:10.6084/m9.figshare.829523		-1303.738044	0.29	1213.36	0.6130	0.7805
		exo	DOI:10.6084/m9.figshare.829522		-1303.736813	1.06	4435.04	0.1671
	bottom	endo	DOI:10.6084/m9.figshare.830388		-1303.730238	5.19	21714.96	0.0002
		exo	DOI:10.6084/m9.figshare.828552		-1303.730703	4.89	20459.76	0.0003

The enantiomeric excess can then be calculated as:

$ee=\frac{c_R-c_S}{c_R+c_S}\times 100\mathrm{\%}$,

where the concentration sums are presented in the last column of the table.

Therefore for styrene: ee = 12.7%

Such enantiomeric excess is of limited synthetic use. The relative ease of various approach pathways must be due to the =CH₂ end of the alkene, which does not provide the sterical hinderance necessary for high stereoselectivity,

Stilbene

attacked face prochirality	dioxirane oxygen	type of approach	calculation	structure	free energy / Hartree	relative energy / (kcal/mol)	Energy difference / (J/mol)	Relative concentration	Sum of concentrations
Re	top	endo	DOI:10.6084/m9.figshare.829523		-1534.699901	0.09	376.56	0.8591	1.8591
		exo	DOI:10.6084/m9.figshare.829522		-1534.700037	0.00	0.00	1
	bottom	endo	DOI:10.6084/m9.figshare.830388		-1534.687252	8.02	33555.68	0.0000
		exo	DOI:10.6084/m9.figshare.828552		-1534.687808	7.67	32091.28	0.0000
Si	bottom	exo	DOI:10.6084/m9.figshare.829524		-1534.68344	10.41	43555.44	0.0000	0.0016
		endo	DOI:10.6084/m9.figshare.829525		-1534.685089	9.38	39245.92	0.0000
	top	exo	DOI:10.6084/m9.figshare.830389		-1534.693818	3.90	16317.6	0.0014
		endo	DOI:10.6084/m9.figshare.830390		-1534.691858	5.13	21463.92	0.0002

Enantiomeric excess for stilbene: ee = 99.8%

The stereoselectivity for the (R,R) enantiomer is very high.

NCI

NCI analysis was performed on two of the transition states from the table above. These are the two possibilities of attack of the top oxirane oxygen on the Si face of the stilbene molecule, endo and exo. Both transition state structure show a considerable amount of attractive interactions (green) between the reactant molecules. As in the endo TS structure the molecules are more eclipsed, one could anticipate its energy to be lower. The ab-initio energies in the table above contradict this prediction (exo 1.23 kcal/mol lower in energy than endo). A closer inspection of the structures and NCI regions suggests, that the extra stabilisation of the exo structure may stem from the interaction of oxygen atoms number 2 and 4, which form a part of the non-fused ring, with hydrogen atoms of the stilbene molecule.

exo	endo
NCI	NCI

QTAIM

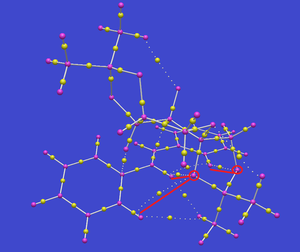
QTAIM analysis allows to find the maximum electron density (bond critical points, BCP) along bonds as well as weaker interactions. The image below shows all the bonds with maximum density (yellow balls) roughly in the middle of the distance between nuclei (purple balls). Interestingly, the interaction suspected from NCI analysis is clearly present on the image below. The two interacting oxygen atoms are circled in red and the three interactions with BCPs marked on them are guided with red lines. As expected for a transition state, there's also an interaction between one of the dioxirane oxygens and one of the carbons of the central double bond.

Jacobsen catalysis transition state energies

Transition states for Jacobsen epoxidation of cis-β-methyl styrene
Form	Approach	Energy / Hartree	Energy difference	Energy difference / J	Relative concentration	Sum of concentrations
S,R	endo	-3383.259559	0	0	1	1.0015
	exo	-3383.253442	0.006117	16060.18116	0.0015
R,S	endo	-3383.25106	0.008499	22314.12126	0.0001	0.0002
	exo	-3383.25027	0.009289	24388.26595	0.0000
Transition states for Jacobsen epoxidation of trans-β-methyl styrene
S,S	endo	-3383.262481	0	0	1	1.0074
	exo	-3383.257847	0.004634	12166.56523	0.0074
R,R	endo	-3383.253816	0.008665	22749.95419	0.0001	0.0003
	exo	-3383.254344	0.008137	21363.69039	0.0002

ee (cis) = 99.96 %

ee (trans) = 99.94 %

Both cis- and trans-methylstyrene can be epoxidated with the Jacobsen catalyst with very high selectivity.

Analysis of the properties of the synthesised alkene epoxides

Optical Rotation experimental

The optical rotation of obtained alkenes will be compared and the math with theory commented on once they are synthesised. -Js4811 23:16, 22 November 2013 (UTC)

Optical Rotation, ECD and VCD simulations

Compound	Optical rotation
	589 nm	365 nm
Styrene S oxide	-54.75	-180.52
Styrene R oxide	54.75	180.52
E-stilbene R oxide	238.69	1011.19

Spectrum	Styrene	E-stilbene
VCD
ECD

Optical rotatory powers of magnitude above 100 degrees are deemed reliable.

Suggestion of alkene for epoxidation

Fig. 4. Proposed epoxide for computational study.

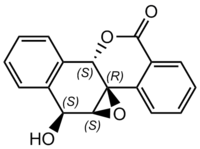
Epoxidation of a double bond embedded in a system of fused rings may be a daunting task for chiral catalysts. The structure of the epoxide is very interesting, though, and may be worth investigating computationally. The compound has been a subject of one known major study and it has been well characterised. It's optical rotatory power in chloroform is known not only at the sodium D-line (-217.8 deg) but also at other wavelengths. Its Circular Dichroism in dioxane has also been recorded. The parent alkene is unlikely to be available commercially and therefore makes it a poor choice for an experimental exercise, unless a smart synthetic route is devised.