Rep:Mod:Brooklyn99

Computational chemistry is very much in its early stages, whereby its results are compared to experimental data, and any discrepancy between the two is always concluded to stem from an over-simplification on the part of the computational calculation. Despite this, when calculations do correlate well with experiment, insights into bonding energies, isomeric stability and other molecular features can be attained. For simple molecules, using small atoms, approximations do not drift far from reality, and accurate models can be analysed, to explain why certain conformations may dominate over others. It requires little effort to understand how much more economical it would be to reliably predict reaction outcomes without the need for 'wet' chemistry experiments. Analyses such as the ones conducted below do have their place in highlighting some of the limitations of computational chemistry, and the hurdles left to overcome before such chemistry can begin to dominate.

Part 1

Dicyclopentadiene

Using Avogadro 1.1, the most stable conformer was first calculated by comparision of the total energies of both the endo- and exo- conformers. An advantage of Avogadro, other than the fact it is freeware, is that it gives a breakdown of the energy contributions to the overall energy. This could be useful for cases where a particular property has a significant influence on the overall energy of the molecule. Avogadro 1.1 only uses classical mechanical optimisation techniques, and will not be as accurate as say the Gaussian package, which uses quantum mechanics.

Figure 1: Diagrammatic representation for the two isomers in question.

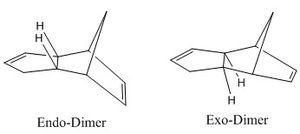
After preparation of a quantity of cyclopentadiene, dimerisation is a spontaneous reaction pathway, and can occur within a few hours if stored at room temperature. The specific reaction follows a [π⁴_s + π²_s] cycloaddition mechanism. It is worth noting that some computer simulators may find difficulty in assigning how many electrons come from each monomer, as the reacting molecules are identical, and be unable to continue. Woodward-Hoffmann rules invoke a 4n+2 electron movement and, assuming thermal activation, predict that the reaction proceeds via a transition state with Huckel topology. This can be evidenced in the models for the endo- and exo- dimers where the hydrogens along the transannular bond are cis- to one another (see figure 1 for a diagrammatic representation).

Figure 2: Diagram depicting secondary orbital overlap contributions.

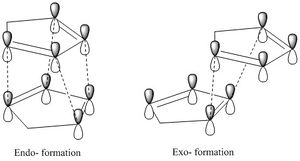
Sterically, the exo- dimer is less encoumbered, and many would predict this to be the thermodynamically favoured product. However, the endo-product is favoured under the usual laboratory conditions. An explanation for this has been found in the form of secondary orbital overlap (SOO), whereby favourable interactions from orbitals not immediately involved in the dimerisation, help stabilise the endo- transition state (see figure 2). This rationale implies a kinetically stabilised endo- product.

Table 1 details the results for calculations run on Avogardo 1.1 with an MMFF94s force field and using a 'conjugate gradients' algorithm. From these results it is first useful to understand that the simulation uses interpolation by working within known data. Since anything in the way of transition states does not have such data associated with it, this software cannot calculate kinetic stability and does not provide a distinction between kinetics and thermodynamics. With this in mind, the total energy results are as expected from a thermodynamic stand-point. The exo- dimer appears thermodynamically more stable. In terms of the individual energy contributions, the angular bending term is the important factor in this calculation. Analysis of the two 'newly formed' bonds shows a C-C-C bond angle of 115.8^o for the exo- product, and a 117.8^o angle for endo- product. Considering an ideal tetrahedral bond angle of around 109^o, the endo- product is furthest from ideality.

Table 1: Total energies of the conformers of dicyclopentadiene including the individual energy contributions.

Energy contributions	File:IMAGE of exo Dimer 1: Exo Dimer	File:IMAGE of endo Dimer 2: Endo Dimer
Stretching energy (kcal mol-1)	3.5429	3.46694
Angular Bending energy (kcal mol-1)	30.77292	33.19072
Stretch Bending energy (kcal mol-1)	-2.04139	-2.08182
Torsional energy (kcal mol-1)	-2.73102	-2.94913
Van der Walls interactions (kcal mol-1)	12.80138	12.35782
Electrostatic energy (kcal mol-1)	13.01372	14.18421
Total energy (kcal mol-1)	55.37344	58.17071

Table 2: Total energies of the semi-hydrolysed conformers of dicyclopentadiene including the individual energy contributions.

Energy contributions	File:IMAGE of 3 3	File:IMAGE of 4 4
Stretching energy (kcal mol-1)	3.30447	2.82306
Angular Bending energy (kcal mol-1)	30.85205	24.68541
Stretch Bending energy (kcal mol-1)	-1.92531	-1.65717
Torsional energy (kcal mol-1)	0.08166	-0.37832
Van der Walls interactions (kcal mol-1)	13.27369	10.63721
Electrostatic energy (kcal mol-1)	5.12107	5.14702
Total energy (kcal mol-1)	50.72286	41.25749

Partial hydrogenation of Dicyclopentadiene

Hydrogenation of a single olefin position is known, with full hydrogenation occurring over an extended period of time, or a larger excess of co-reagents. To determine which of the two olefin positions provides the more favourable mechanism, Avogadro 1.1 was used to calculate the energies of the two possible products (see figure 3 for compounds 3 and 4), with the theory being that the lower energy product would be the single hydrogenation most likely to occur first. But once again, this approach will ignore any kinetic rates, and so reference to experimental results would help make sense of the data.

The calculated results in table 2 show that Dimer 4 is the lowest energy hydrolysed dicyclopentadiene. Comparing this to experimental preference found indicates that dimer 4 is indeed the most favourable semi-hydrogenated product, owing to thermodynamic stability. Again, angle bending energy is the pivotal value in these results. Relief of bond strain from conversion of sp² centres into sp³ centres is more pronounced in the case of dimer 4, it is more stabalised. Van Der Waals energy also has a notable influence. The hydrogens gained by molecule 4 are in close proximity to hydrogens on the opposite side of the ring, offering attractive Van Der Waals interactions that stabalise the molecule. Hydrogens added to molecule 3 do not have the right spacial geometry to have an equivalent stabalising effect. This results in a lower Van Der Waals energy for molecule 4.

Taxol Intermediates and Atropisomerism

Atropisomerism is a specific form of chemical isomerism in which two of the same compound differ in conformation due to high energy rotational barriers, restricting interconversion and allowing single atropisomers to be isolated. Using Avogadro 1.1, it is possible to manually adjust a molecule in real-time. In other words, the molecule may be stretched and skewed by the user, and the software will then work to position the molecule back into its most stable geometric position. This technique was used to manipulate Taxol intermediates, adjusting the cyclohexane ring to explore its atropisomers, as is explained below.

Table 3: Total energies of molecules 9 and 10 including the individual energy contributions.

Energy contributions	9 (Chair)	9 (Twist boat)	10 (Chair)	10 (Twist Boat)
Stretching energy (kcal mol-1)	8.18060	8.35332	7.14326	7.25139
Angular Bending energy (kcal mol-1)	32.40116	32.01882	22.41039	23.21232
Torsional energy (kcal mol-1)	-0.58061	2.23819	-1.88221	1.16900
Van der Walls interactions (kcal mol-1)	35.39873	37.70051	32.11406	33.60176
Electrostatic energy (kcal mol-1)	0.43823	0.31935	0.83171	0.83810
Total energy (kcal mol-1)	76.46166	81.62709	61.03627	66.58689

The Oxy-Cope rearrangement is based on a [3,3]-Sigmatropic rearrangement and can be a very facile reaction. Figure 3 shows the starting compound, and two possible atropisomers 9 and 10 resulting from an Oxy-Cope rearrangement. These two products were analysed using Avogadro 1.1, with a detailed summary included in table 3. In total, four atropisomers could be calculated as being a stable state for the molecule. Each of molecules 9 and 10 can be broken down into two further atropisomers, owing to the chair and twist boat conformations possible for the internal 6-membered ring.

Table 4: Total energies for compounds 17 and 18 including individual energy contributions.

Energy contributions	Ketone 17 chair	Ketone 18
		Chair	Twist boat
Stretching energy (kcal mol-1)	15.83564	15.08489	14.39695
Angular Bending energy (kcal mol-1)	31.34892	30.79938	28.34193
Torsional energy (kcal mol-1)	13.71665	9.76748	13.77708
Van der Walls interactions (kcal mol-1)	53.60543	49.56976	50.54338
Electrostatic energy (kcal mol-1)	-6.93696	-6.11651	-6.36955
Total energy (kcal mol-1)	109.13875	100.62772	102.20804

An isolated cyclohexane ring experiences its lowest energy conformation in the chair state. This is evidenced in the results found here, as in both cases (either ketone up or ketone down) the chair conformation sits at a lower total energy than the twist boat. The two larger energetic contributions that cause this were found to be torsional energy and Van Der Waals energy.

Figure 3: Schematic detailing the Oxy-Cope rearrangement occurring to produce Taxol intermediates 9 and 10. For original report, see Stephen W. Elmore and Leo A. Paquette: The First thermally-induced Retro-Oxy-Cope Rearrangement.

Figure 4: Schematic of di-thiols 17 and 18.

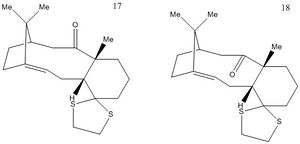
Di-thiols 17 and 18 (see figure 4), derived from Taxol, are more complex molecules, used here to test computational power and begin to expose limitations of the software. Table 4 summarises results using the same Avogadro 1.1 setup as before. Molecule 17 was resolved further using Gaussian, which also calculated NMR and vibrational data. In this way, the spectral data could be compared to literature in order to gauge how accurately the molecule had been modeled.
It was found that, whilst molecule 17 only existed in a single atropisomer, molecule 18 could form both a chair and twist boat conformation, as seen for Taxol intermediates 9 and 10. In continuing with the comparison to molecules 9 and 10, the 'ketone down' position, i.e. with carbonyl pointing away from the bridging alkyl groups, are always the thermodynamically more stable.

NMR Analysis

Calculated NMR spectra for compound 17.

	1H NMR	13C NMR
Spectrum

---

Comparison of calculated¹H NMR spectra with literature

¹H NMR assignment comparison between computed spectrum and literature for compound 17

Computed δ(ppm) DOI:10042/28052	Integral	Reported Values δ (ppm)
5.15	1	4.84, (dd, J=7.2,4.7Hz, 1H)
3.45	1	3.40-3.10 (m, 4H)
3.29	2
3.21	1
3.02	2	2.99 (dd, J=6.8, 5.2 Hz, 1H)
2.55	3	2.80-1.35 (Series of m, 14H)
2.49	1
2.28	4
2.16	1
2.08	1
1.72	1
1.67	1
1.47	3
1.35	1
1.18	3	1.10 (s, 3H)
1.10	3	1.00 (m, 1H)

¹³C NMR assignment comparison between computed spectrum and literature for compound 17

Computed δ(ppm) DOI:10042/28052	Reported δ (ppm)
217.12	218.79
145.11	144.63
125.50	125.33
89.10	72.88
59.10	56.19
54.40	52.52
53.43	48.50
51.87	46.80
47.74	45.76
47.63	39.80
44.17	38.81
42.50	35.85
38.63	32.66
35.45	28.79
32.24	28.29
28.43	26.88
26.39	25.66
26.26	23.86
21.45	20.96
19.74	18.71

Figure 5: Graph of results for ¹³C NMR. Displayed is the difference between calculated and literature values, in other words, the larger the bar, the larger the deviation from known values.

The calculated proton NMR spectrum shows some limitations. Gaussian has arbitrarily grouped protons of near-identical chemical shifts together as 'degenerate' sets. This is despite the protons being located several bonds apart, and in similar, but different environments. To work around this problem, the chemical shifts for protons belonging to each of the three methyl groups were averaged to form three new chemical shift values. These values were used in place of the 9 original methyl shifts, which will account for environmental averaging caused by rapid rotation about the methyl single bonds. This is more reminiscent of how a real molecule would behave.

The calculated ¹³C spectrum correlates very well to literature values. The only notable exception is for the calculated 89.10 chemical shift due to the heavy atom effect (highlighted in figure 5). This refers to the carbon atom directly bonded to two sulphur atoms, which have more associated electrons and are more complex. For this reason, approximations used by Gaussian are adhered to more poorly than the lighter Hydrogen or even carbon atoms. It is possible to invoke pseudo-potentials, where the software models the inner electrons of a heavy atom as a single shell, and a valence set of electrons on top of this. However, it is inevitable that, as atom sizes increase, they become more complex and harder to model. This is an important computational limitation that limits computational chemists to only a certain number of compounds.

Part 2

The aim of this section is to provide an analysis of the crystal structure of the Jacobsen catalyst and the Shi catalyst, and to retrieve some information that will help explain the enantioselectivity of the catalysts. Crystal structure data was extracted from the Cambridge Crystal Database, and analysed using Mercury, an accompanying software package that allows the user to explore database structures and view crystal packing in 3D.

Shi Catalyst Precursur

Figure 6: (Top)Crystal structure and (bottom) schematic for the Shi Precatalyst.

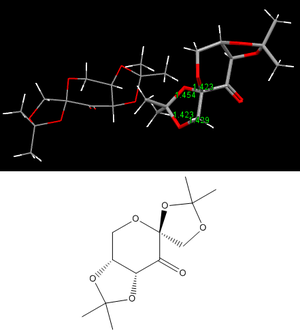
The fructose-derived ketone shown in figure 6 is the pre-catalyst first synthesised by Shi et. al. used to epoxidise alkenes with a high degree of enantiomeric excess (ee), specifically for trans-substituted and trisubstituted alkenes. Transition state analysis in a subsequent section provides some computational evidence for this. The crystal structure present in the same figure is one of two structures in the unit cell. Values are included for C-O bond lengths within one of the 5-membered rings, one of which appears to be larger than the expected (C-O) value of 1.42 Å. The bond distance value of 1.454 Å is most likely as a result of a lone pair donation from the oxygen of the bond, into the adjacent σ*C-O orbital, weakening the C-O bond in question. The anomeric effect allows the equitorial position to be favoured over the axial, due to positive orbital overlap that stabalises the equitorial conformation. This effect is not observed for any of the other possible candidates for anomeric interactions, largely due to the electron widthdrawing influence of the carbonyl bond.

Jacobsen Catalyst Precursur

Figure 7: (Top)Crystal structure and (bottom) schematic for the Jacobsen Precatalyst.

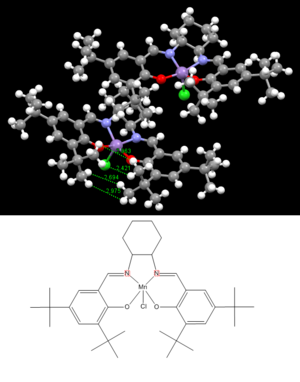
This metal-centred precatalyst favours the epoxidation of unfunctionalised alkyl- and aryl- compounds. Again, the resulting catalyst appears to have high enantioselectivity. Favourable Van Der Waals (dispersion) forces are attractive forces that occur over longer-than bond-length distances. For two hydrogen atoms located approximately two Van Der Waals radii (2.4 ANGSTROMS) apart, an attractive force will be present, stabilising the molecule. Figure 7 contains the crystal structure for the Jacobsen catalyst, and highlighted are the H….H atom distances on the two tertiary butyl groups in close special proximity to one another. One of these distances was found to be 2.421 ANGSTROMS, an ideal distance for dispersion forces. Another interaction may exist where an interatomic distance of 2.694 ANGSTROMS is observed. The gap separating the two groups in question is quite possibly essential in restricting the active site areas on the catalyst, in other words, stopping attack from this angle.

Optical Rotation analysis

Certain analytical techniques may be modeled with computer software, with optical rotation analysis being one such method. Observation of the parity of the resulting value can show which enantiomer has been modeled, and allow the computational chemist to deduce which enantiomer they have made in the lab, by comparison to an experimentally measured valued. Making sense of the magnitude of these values, however, is less straight forward because of sensitivity issues with light conditions, temperature, pressure etc. Calculation of optical rotation values for β-methyl styrene oxide and 1,2-dihydronapthalene oxide. In order to carry out this calculation, each molecule was first drawn using ChemDraw 13.0, mechanically optimised with Avogadro 1.1 in the same way previously discussed and following this, a Gaussian optical rotation input file was generated. The Cambridge B3LYP density functional method was used, and the input file was constructed to ask for absorptions at 365nm and 589nm.

Table 5: Optical rotation values at 589 nm.

Compound	Optical rotation (o)
	Calculated prediction	Literature Value
(R)-styrene oxide	-30.12 DOI:10042/28249	-24
(S)-styrene oxide	+30.45 DOI:10042/28250	+32.1
((R,S)-1,2-dihydronaphthalene oxide	+155.81 DOI:10042/28248	+133
(S,R)-1,2-dihydronaphthalene oxide	+35.86 DOI:10042/28251	-144.9

From table 5, it is evident that calculations show strong correlation with literature results. Minor deviations are not important here, because the aim of this calculation was to assign R or S to each enantiomer, and prove that two seperate enantiomers exist. The S,R conformation for 1,2-Dihydronapthalene might at first seem anomalous, but upon inspection of the mathematics based around a 365^o circle, 35.86^o - 180^o = -144.14^o. Envisaging a sinosoidal curve with a phase length of 180^o may help with this. The resulting value lies close to the literature value. Optical rotation values for 365nm are not currently present in literature, and no useful information has been attained in its regard.

Transition state analysis

Calculations have been computed for various transition states in an attempt to find the true geometry of reacting olefin with catalyst. The following section involves collecting free energy values for these transition states, determining which state is the lowest energy for each enantiomeric version of the olefin, and calculating enantiomeric excess values from the data. In this way, one can have an informed view on which catalyst has a preference for which enantiomeric configuration.

Shi Catalyst Transition States

From analysis of the transition state free energies calculated as a result of Shi epoxidation for β-Styrene Oxide, the lowest R,R transition state energy was found to be -1343.032443 a.u. The lowest S,S transition state energy was found to be -1343.024742 a.u. The overall lowest energy transition state, and therefore the preferred one, is the R,R variation. The difference in energy between these two diastereomers is a free energy (ΔG) of -20.218977 kJ/mol

Using a variation of the Gibbs Free Energy equation, ΔG = -RT ln K, a value for the equilibrium constant was calculated to be 3514.8.

Following this, the enantiomeric excess was calculated with the equation (K-1)/(K+1) x 100, where K is the rate constant calculated above. This yields a value of 99.94% enantiomeric excess. This means that 99.94% of the total yield is the R,R enantiomer.

This same calculation is also done with 1,2-Dihydronapthalene below:
Lowest energy R,S diastereomer = -1381.134059 a.u.
Lowest energy S,R diastereomer = -1381.136239 a.u.

ΔG= -5.723590 kJ/mol
K= 10.1
EE= 82.96% S,R enantiomer preferred.

Jacobsen Catalyst Transition States

The following results are from transition state analysis using β-Methyl Styrene: Lowest energy R,S diastereomer = -3383.251060 a.u.
Lowest energy S,R diastereomer = -3383.259559 a.u.

ΔG= -22.3141262 kJ/mol
K= 8190.9
EE= 99.97% S,R enantiomer preferred.

The following results are from transition state analysis using 1,2-Dihydronapthalene: Lowest energy R,S diastereomer = -3421.359499 a.u.
Lowest energy S,R diastereomer = -3421.369033 a.u.

ΔG= -25.0315189 kJ/mol
K= 24541.2
EE= 99.99% S,R enantiomer preferred.

It is clear that, energetically, certain transition states are preferred over others, leading to each catalyst preferring a substrate with a certain stereochemistry. Research through literature tells a slightly different story. Enantiomeric excess percentages are much closer to 50% than the high values calculated above. As alluded to in the introduction, the computational approach will suffer from lack of detail, including no inclusion of possible side-reactions, not to mention many more potential transition states than the 4 main alignments calculated during this write-up. Often, large compounds may be simplified slightly, in order to make them computable, in order to give a less accurate, but informative result.

Further Study

Figure 8: Indene. A possible example

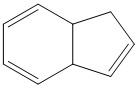
in order to analyse other epoxides, olefins with cheap precursurs would be ideal. Furthermore, known literature papers on specific epoxidation reactions may prove useful. The example given in figure 8 can be hydrogenated from the readily available indene. It may prove useful to compare this case to the previously discussed 1,2-Dihydronapthalene example.