Rep:Mod:BirdistheWord
Module 3: Transition States and Reactivity
All calculations are carried using the Gaussian 9.0/Gaussview 3.0 or 5.0 Suite, whether on laptop or submitted to the Imperial SuperComputerAtNight (SCAN). Absolute energies are reported in Hartrees, and relative energies in kcal mol-1. The conversion factor used to calculate relative energies is 1 Hartree = 627.509kcal mol-1. Bond lengths are reported in Angstroms (Å) to 2d.p., and bond angles in degrees to 1d.p. Vibration frequencies are reported in wavenumbers (cm-1) to the nearest whole integer, and intensities of IR peaks in arbitrary units to the nearest whole number unless that results in recording a value of 0; in that case 2d.p. suffices.
The Cope Rearrangement Tutorial
In this tutorial, the Cope rearrangement of 1,5-hexadiene will be investigated. Below is the reaction scheme:
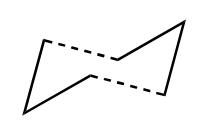
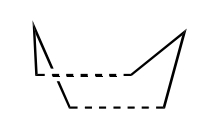
It has been determined for the above reaction the pathway it proceeds by. This is via the boat or chair transition state in a concerted pathway. The boat TS lies several kcal mol-1 higher in energy than the chair TS. These TS's are shown below:
 |
 |
Optimising the Reactants and Products
(a)
A molecule of 1,5-hexadiene was created in Gaussview with an anti linkage (antiperiplanar) for the central 4 C atoms, by changing the dihedral angle to 180.0°, and was subsequently "Cleaned" using the Clean function. The structure was then optimised using the following key commmands in the input (.gjf) file that was submitted to Gaussian:
| Method: HF |
| Basis Set: 3-21G |
| Type: OPT (optimisation) |
| %mem: 250MB |
It should be noted that although the %mem (memory allocated to the calculation) value here was set at 250MB, subsequent calculations didn't require this value to be set (i.e. the default setting sufficed). The following output file was created:
https://wiki.ch.ic.ac.uk/wiki/images/5/59/REACT_ANTI_OPT.LOG
and an image of the optimised geometry is below:

The Summary section was accessed under the Results menu and the absolute energy was recorded as -231.69253506 Hartrees. To determine if the optimised structure had symmetry, the Symmetrize function was used, and the point group was determined to be Ci.
(b)
Another molecule of 1,5-hexadiene was created in Gaussview, but this time with a gauche linkage (~60° apart) for the central 4 C atoms. This was submitted for optimisation as well, using the same key commmands for the input file as in part (a). It is expected that this optimised conformation would be higher in energy than the anti conformation in (a) due to increased steric repulsion between the vinyl groups either side of the central C-C bond, as they are located spatially closer to each other in the gauche conformation. The following output file from the job was obtained:

The Summary section was again accessed and the absolute energy was recorded as -231.69153035 Hartrees. This is indeed higher in energy than the anti conformation as expected. The molecule had symmetry and the point group was determined to be C2.
(c)
When calculating activation energies and enthalpies, the lowest energy conformer of the reactant molecule is used as the reference. Based on the previous energies calculated for the rpevious conformers, a guess was made at the lowest energy conformer, which was then optimised to see if it was the lowest energy conformer. This guess structure had an anti linkage, and the input file key commands the same as in (a) and (b). The optimised structure was thus:
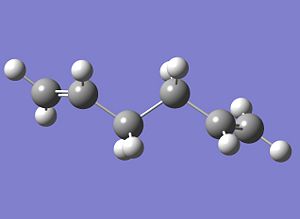
The absolute energy of this conformation was found to be -231.69260235 Hartrees. This is lower in energy than the other two conformers, and so would seem to be the lowest energy conformer, of the three. It should be noted the slightly different orientation of the vinyl groups, whereby this conformer has them cis/syn and the other has them trans/anti. The point group was also found to be C2.
(d)
Appendix 1 on the Module's wikipage shows the lowest energy conformers of 1,5-hexadiene, their absolute/relative energies, and their point groups. Comparing the information in the table to the information obtained, the structures were identified thus:
| Low Energy Conformer | Identity |
|---|---|
| (a) | anti2 |
| (b) | gauche4 |
| (c) | anti1 |
Two key points were noted upon comparing with Appendix 1. Firstly, the predicted lowest energy conformer (c) was not so, as there was a lower energy conformer: gauche3. Secondly, the conformer created that was anti1 looked slightly different in spatial orientation compared to the image in the table; as it turned out, the enantiomer of anti1 in the table, was optimised in (c).
(e)
Anti2 conformation of 1,5-hexadiene, with Ci symmetry, was already located in (a). The absolute energy of this optimised conformer was very similar to the one given in the table; to 5d.p. they match.
(f)
Having confirmed that the anti2 conformation optimised was the same as the one in Appendix 1, it was re-optimised at a higher level. The following key commands in the input file were used:
| Method: DFT-B3LYP |
| Basis Set: 6-31G* |
| Type: OPT (optimisation) |
6-31G* means 6-31G(d), and under the "Link 0" tab the name of the .chk file was changed to avoid overwriting.
The absolute energy was recorded as -234.61170276 Hartrees. Comparing the HF and DFT-optimised geometries of anti2, there is no major change in overall geometry; bond lengths and angles differ insignificantly, and the anti linkage in both cases has a dihedral angle of 180.0°. More importantly, the absolute energies differ quite significantly, by ~3 Hartrees.
(g)
A frequency calculation was carried out on the anti2 conformer. This was done to confirm that a minimum on the potential energy surface was found for the optimised anti2 conformer, by observing all vibrational frequencies to be real and positive. This was also done to provide the additional terms needed on top of the reported absolute energies so as to be able to compare with experimentally measured values. The following key commands on the input file were used:
| Method: DFT-B3LYP |
| Basis Set: 6-31G* |
| Type: FREQ (frequency) |
Looking at the .log file ouput, all the vibrational frequencies were determined to be positive and real, therefore indicating that the optimised structure was indeed a minimum. The IR spectrum was also obtained:

The following list of energies, under the "Thermochemistry" section, were also obtained (all in Hartrees):
Sum of electronic and zero-point Energies= -234.469211 Sum of electronic and thermal Energies= -234.461854 Sum of electronic and thermal Enthalpies= -234.460910 Sum of electronic and thermal Free Energies= -234.500825
Optimising the "Chair" and "Boat" Transition Structures
Appendix 2 on the Module wikipage shows the chair and boat TS's. Each one contains two C3H5 allyl fragments positioned approximately 2.2Å apart, with the chair TS having C2h symmetry and the boat TS having C2v symmetry.
(a)
The chair TS will be optimised first. An allyl fragment (CH2CHCH2) was created in Gaussview, and then optimised as follows:
| Method: HF |
| Basis Set: 3-21G |
| Type: OPT (optimisation) |
As can be seen above, the optimised geometry looks like one half of the TS's.
The chair TS was then built using this optimised allyl fragment twice, keeping the distance between the terminal ends of the fragments at 2.2Å, and an input file was saved for this "guess" structure.
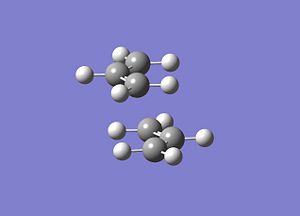 |
Subsequently both TS are optimised using a selection of methods, which are described below. All methods of optimising/frequency analysis of the TS henceforth are done using:
| Method: HF |
| Basis Set: 3-21G |
(b)
The "guess" chair TS was then submitted for optimisation and frequency analysis with the following key commands:
| Type: OPT+FREQ (optimisation+frequency) |
| Optimisation to a: TS(Berny) |
| Calculate Force Constants: Once |
| Additional Keywords: Opt=NoEigen |
The frequency analysis will confirm if the optimised geometry is a TS by the presence of a single negative (imaginary) frequency. The force constants (force constant matrix or Hessian) are calculated "Once" to determine where the negative direction of curvature on the potential energy surface (PES) is, and hence procure the optimised TS; this the method used here to compute the TS. The additional keywords "Opt=NoEigen" stop the calculation from crashing if more than one negative frequency is detected as the optimisation moves along the (PES); note this doesn't correspond to the negative frequency of the final optimised TS, but just those detected "along the way", until the final TS is reached. This occurs if the guess TS isn't close enough to the actual TS geometry.
The optimised chair TS geometry is as follows:

Looking at the image above, it can be seen that it corresponds to the chair TS found in Appendix 2, confirming that the optimisation proceeded successfully. The frequency analysis also gave a single imaginary frequency of -818cm-1, confirming that the optimised geometry is a TS. The animated vibration corresponding to the Cope rearrangement is below:
Vibration |
(c)
The chair TS was again optimised from the "guess" structure, this time using the Frozen Coordinate Method. Firstly, the bonds being made/broken during the rearrangement are frozen using the Redundant Coordinate Editor, and the rest of the molecule minimised:
| Type: OPT (optimisation) |
| Optimisation to a: Minimum |
| Calculate Force Constants: Never |
The input line will now include the command "Opt=ModRedundant".
(d)
Here is the output file geometry:
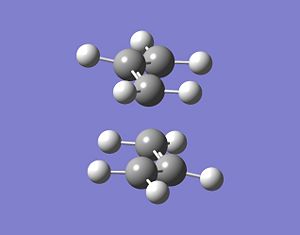
This optimised geometry is pretty much the same as the one in (b), except for those frozen bonds, which are still set at 2.2Å. Now this geometry will be optimised along these bonds as well, to find the optimised TS geometry, by differentiating along them. The following input file was thus created:
| Type: OPT (optimisation) |
| Optimisation to a: TS(Berny) |
| Calculate Force Constants: Never |
| Additional Keywords: Opt=NoEigen |
The following output geometry was created:
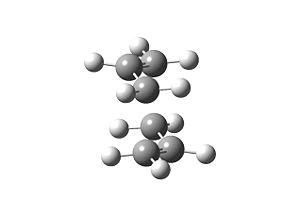
The optimised TS geometry computed here is very much the same as that found in part (b); both have bond breaking/forming bond lengths of 2.02Å, and are spatially orientated the same way.
(e)
The boat TS will now be optimised. This was performed using the QST2 method. In order for this method to work, the reactant and product atoms must be numbered in the same way as follows:
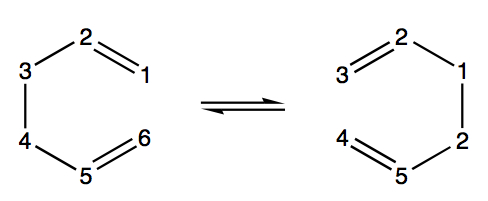
This accounts for the change of bonding between each numbered atom, but keeps their "positions" the same. Therefore, two molecules of the optimised anti2 1,5-hexadiene were read as multiple geometries in a single Gaussview window, and were viewed side by side. Then they were placed in such a way as to be mirror images of each other. One molecule is shown below, being one side of the mirror images:
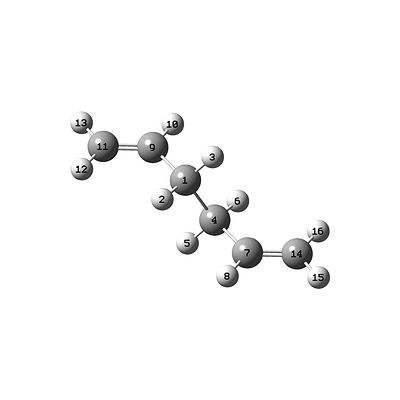
The other side is the mirror image molecule, which is the "product" molecule, and the atoms were labelled with numbers for both molecules. The "product" molecule is the one that then needs its numbering changed to allow QST2 to work. This was done using the Atom List Editor, in such a way as both molecules correspond to each other like the numbering structure in the "Correct numbering" image. The QST2 calculation was then set as follows:
| Type: OPT+FREQ (optimisation+frequency) |
| Optimisation to a: TS(QST2) |
| Calculate Force Constants: Never |
| Additional Keywords: Opt=NoEigen |
The resultant optimised geometry looked as follows:
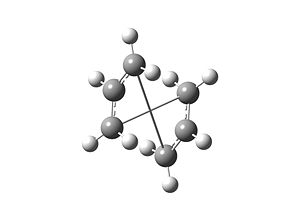
The C-C bonds crossing between the allyl fragments are a clear indication that this optimisation has gone wrong, even though it looks like the chair TS, although more dissociated. This has happened because the calculation linearly interpolated between the reactant and product molecules by just translating the top allyl fragment across to match the bottom fragment on the other side. It didn't consider any rotation about the central C-C bond. As a result, the boat TS can't be thought to be derived from these input reactant/product structures using QST2, i.e. it requires reactant and product structures that have a closer resemblance to the TS to be determined. This means they must be closer to the TS on the PES. Therefore, the reactant and product molecules in the original input file were altered. The central C-C-C-C (i.e. C9-C1-C4-C7 in the image above) dihedral angle was changed to 0.0°, and the inside C-C-C (i.e. C7-C4-C1 and C4-C1-C9 above) angle was changed to 100.0°. This led to the following reactant geometry:

The product molecule was changed in the same way. The altered input file was then submitted for OPT+FREQ as previously, and the optimised geometry was found thus:
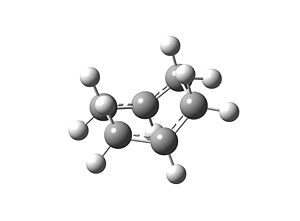
As can be seen above, the optimisation has worked and the boat TS has been located. There was only one imaginary frequency found from the analysis, which was -840cm-1, thus confirming this geometry was a TS. The motion is visualised below:
Vibration |
(f)
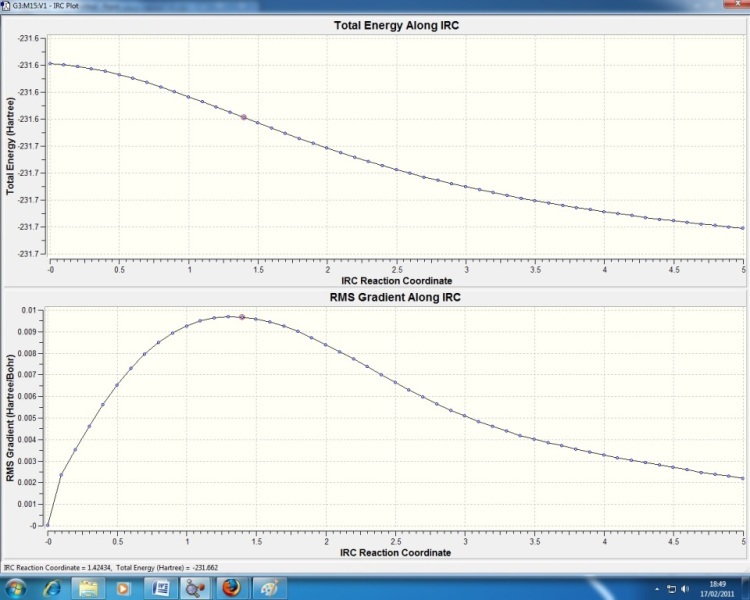
Looking at the chair/boat TS, its almost impossible to just guess what original reactant/product conformer they lead to on the PES along the reaction coordinate (e.g. anti1, gauche4 etc.). However, the Intrinsic Reaction Coordinate (IRC) method, which is part of the Gaussian program, can follow the PES along the steepest slope from the TS to find the reactant/product structure at a local minimum. Taking the chair TS from part (b), it was submitted as an IRC job with the following key commands:
| Type: IRC |
| Optimisation to a: Minimum |
| Compute Reaction Coordinate: Forward |
| Calculate Force Constants: Once |
| No. Points along IRC: 50 |
The reaction coordinate is the same in the forward and backwards directions (reactant and product the same), so just Forward was chosen. The resultant geometry found did not correspond to any minimum geometries in Appendix 1. N.B. IRC Calculation .log file attached to email with Mod links, as too large to upload.