Rep:Mod:Ben12005
Inorganic Module: Bonding (Ab intio and density functional molecular orbital)
Introduction
Computational chemistry is widely used to investigate the structure and bonding of complexes. This module will focus on inogranic computational chemistry. Whilst many organic systems have relatively simple bonding, the bonding in inorganic compounds and complexes is often not as straight forward. Electron density analysis can be used to provide information on the bonding and local interactions between atoms. Computaional studies can also be used to characterise transition states and activated complexes as well as investigating properties such as IR and NMR spectra and dipole moments. We will start by evaluating two small D3H complexes, BH3 and TlBr3, then move on to the analysis of isomers of Mo(CO)4L2.
BH3
Optimising a molecule of BH3
Initailly, a molecule of BH3 was created using Gaussveiw, the B-H bond lengths were set to 1.5 angstrom. The molecule was then optimised, table 1 gives a summary of this optimisation. A low accuracy basis set, 3-21G, was used here to allow for speedy calculations. The total energy curve was observed in Gaussview and shows the program traversing the PES of BH3 to find the minimum energy structure. The RMS gradient graph was also available to see the gradient going to zero as a minimum is approached, this optimised structure is the stable structure of borane. The output file from the optimisation is available here.
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Energy | -26.4622 a.u. (-6.948x104 KJmol-1) |
| RMS Gradient Norm | 0.00020672 a.u. |
| Point Group | D3H |
| Bond Length | 1.19 angstrom |
| Bond Angle | 1200 |
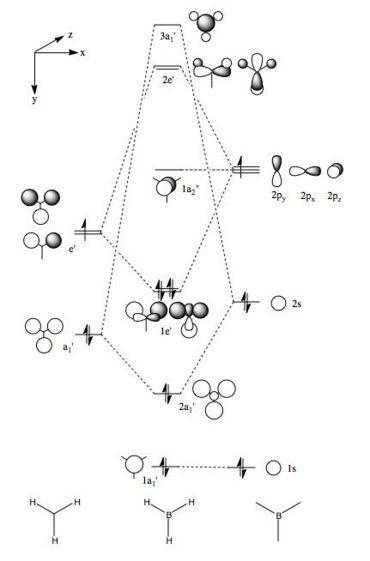
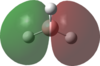
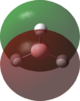
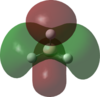
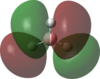
MO analysis of BH3
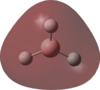
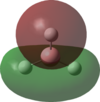
An MO analysis of BH3 was run and the computed MOs are displayed in the table below.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Energy (a.u.) | -6.766 | -0.515 | -0.353 | -0.353 | -0.682 | 0.166 | 0.180 | 0.180 |
| Image | 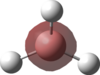 |
 |
 |
 |
 |
 |
 |
|
| Symmetry Label | 1a1' | 2a1 | 1e' | 1e' | 1a2" | 3a1' | 2e' | 2e' |
| The computed MOs of BH3 can be compared with a qualitative MO diagram, as shown here. The LCAO representations compare well with the images displayed in Gaussview. One noticable difference is that the computed MOs give a lower energy to the 3a1 MO and put this below the degenerate 2e' MOs, qualitatively these MOs are the other way round. This happens because qualitative MO theory is unable to accurately predict MO energies. |
NBO analysis was performed using the output from the population analysis, a large amount of information about hybridisation and the nature of the B-H bonds can be taken from this. The NBO charges for the boron and hydrogen atoms were found to be 0.331 and -0.11 respectively. This is characteristic of boron being electron dificient in borane.
Vibrational Analysis of BH3

BH3 is a non-linear molecule and as such shows 3N-6 vibrational frequencies. These six frequencies are shown above. The IR spectrum for BH3 only exhibits 3 stretches since there are two sets of degenerate vibrational frequencies (2 and 3 and 5 and 6)and one of the frequencies is totally symmetrical (4) and is therefore not IR active.
TlBr3
An optimisation and frequency analysis of TlBr3 was performed. A summary of the optimisation is shown in table 2. This time a medium basis set (D95V) and a pseudo potential (Los Alamos ECP) were used since there are a large number of electrons in the complex. Pseudo potentials model the core electrons of an atom and can be used to recover some of the relativistic effects observed with large atoms. The output file from the optimisation is available here.
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Charge | 0 |
| Spin | Singlet |
| Energy | -91.218 a.u. (-2.395x105 KJmol-1) |
| RMS Gradient Norm | 0.00000090 a.u. |
| Point Group | D3H |
| Bond Length | 2.65 angstrom |
| Bond Angle | 1200 |
A frequency analysis is preformed to confirm that the optimised structure is a minimum. The frequency analysis is esentially the second derivative of the PES, so if the frequencies are found to be all positive a minimum has been reached. The same basis set is used for both the optimisation and frequency analysis to ensure an accurate comparison can be made between the two calculations. The low frequencies found were -3.4213cm-1, -0.0026cm-1, -0.0004cm-1, 0.0015cm-1, 3.9367cm-1, 3.9367cm-1. These represent the vibrations of the molecules centre of mass. The lowest "real" normal mode calculated was 46.4289cm-1
Isomers of Mo(CO)4L2
In this section we are going to use computational methods to investigate the cis and trans isomers of Mo(CO)4(PPh3)2. However, due to the computational expensive of calculating the full molecule, the phenyl rings are replaced by Cl atoms. The cis (left) and trans (right) structures are shown below.
|
|
An optimisation was preformed intially using the B3YLP method and a LANL2MB basis set to give a rough calculation before altering the geometries then optimising again, with the LANL2DZ basis set, to give the right minima. A frequency analysis was done to confirm whether a minima was reached. The low frequencies calculated are close to zero, which means the optimised structure is a minimum. The energies of the cis and trans isomers were found to be -623.577 a.u. (1.637 x106 KJmol-1) and -623.576 a.u.(1.637 x106 KJmol-1).
The output files for the final optimisation can be found here: Cis DOI:10042/to-7102 Trans DOI:10042/to-7103
The output files for the frequency analysis can be found here: Cis DOI:10042/to-7104 Trans DOI:10042/to-7105