Rep:Mod:BYL109 module 3

The Cope Rearrangment

The Cope Rearrangement is the thermal isomerisation of a 1,5-diene to its 1,5-regioisomer, where the thermodynamically more stable regioisomer is usually favoured. It involves a [3,3]-sigmatropic shift, whose mechanism has long been under scrutiny. The general consensus is that the reaction occurs via a transition state, with either a chair or boat structure, the chair usually more thermodynamically stable.

Cope Rearrangement reaction

Through the use of the computational methods at our disposal, the aim is to determine the lowest energy minima of the C₆H₁₀ potential energy surface (PES) and transition structures of the molecule in order to affirm which mechanism is used to form the product.

Optimisation

Firstly, the Gaussview program was used to draw the 1,5-hexadiene molecule, with an antiperiplanar (a.p.p) conformation for the four central C-C bonds. The conformation was drawn using the dihedral angles, with the knowledge that a.p.p conformations have a dihedral angle of 180° (see Anti 2 conformer in Table 1). The molecule was then 'cleaned', before submission to the HPC centre for optimisation using the Hartree-Fock, 3-21G method. A similar process was used for the gauche conformations, using dihedral angles of 60° with the same level of theory (c.f. Gauche 3 conformer). An alternative gauche conformation was also drawn, using an angle of 90° (see Gauche 4 conformer).

In accordance with Appendix 1, the conformers were then compared to the structures optimised shown in Table 1, to identify the structures. The summary of results is shown below:

Table 1: Summary of results from the optimisations of 1,5-hexadiene conformers

	Anti (2) conformer	Gauche (3) conformer	Gauche (4) conformer	Anti (2) conformer re-optimised
Jmol	Anti 2 conformer	Gauche 3 conformer	Gauche 4 conformer
Image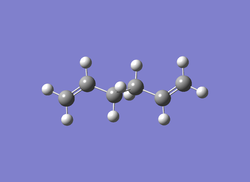
Calculation Type	FOPT	FOPT	FOPT	FOPT
Calculation Method	RHF	RHF	RHF	RB3LYP
Basis Set	3-21G	3-21G	3-21G	6-31G
Charge	0	0	0	0
Spin	Singlet	Singlet	Singlet	Singlet
E(RHF/RB3LYP)	-231.69254 a.u.	-231.69266 a.u.	-231.69153 a.u.	-234.55970 a.u.
RMS Gradient Norm	0.00001339 a.u.	0.00000586 a.u.	0.00000903 a.u.	0.00004445 a.u.
Dipole Moment	0.0003 Debye	0.3406 Debye	0.1281 Debye	0 Debye
Point Group	Ci	C1	C2	Ci
Job cpu time	42.2 sec	1 min 18.8 sec	45.3 sec	1 min 17.9 sec

Files showing proof of calculations:

DOI:10042/to-10192 Anti 2 optimsation

DOI:10042/to-10193 Gauche 3 optimisation

DOI:10042/to-10194 Gauche 4 optimisation

Comparison with Appendix 1 shows that the energies agree with the values shown in Table 1. The gauche3 conformer is seen to be the one with the lowest energy, and is therefore the most thermodynamically stable. This agrees with previous knowledge about the Gauche effect, which uses hyperconjugation as a reason for its noted stability. Donation of electron density from the C-H σ to the C-H σ* orbital is considered favourable and therefore lowers the energy. However, the anti2 conformation is actually the one considered to be the reacting molecule for the reaction.

Now comparing the optimisations of the anti conformation at different levels of theory, the Hartree-Fock and DFT methods resulted in little difference seen between the structures of the anti 2 conformations. Labelling the carbons from left to right for the anti 2 conformer (c.f. Table 1), the C=C bonds (C1-C2/C5-C6) are 1.32 and 1.34Â for the HF and DFT methods respectively. For the C-C bonds, C2-C3/C4-C5 are both 1.51Â and C3-C4 are both 1.55Â from each method of optimisation. This therefore confirms little difference between the two optimisations, with the energies only altering slightly for the structure optimised at the higher level of theory.

Carrying out a frequency calculation with the optimised B3LYP-structure of the Anti 2 conformer gave the energies below. If time had allowed it, a frequency calculation could have been run at 0K to confirm the sum of electronic and zero point energy value (E=E_elec +ZPE) agrees with the one shown in the data below:

Energies of anti2 conformer (found in Frequency calculation log. file)

(E=Eelec +ZPE)	-234.416252
(E=E+Evib+Erot+Etrans)	-234.408952
(H = E+RT)	-234.408008
(G = H-TS)	-234.447896

The first of these is the potential energy at 0K including the zero-point vibrational energy (E = Eelec + ZPE), the second is the energy at standard conditions which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans), the third contains an additional correction for RT (H = E + RT) which is particularly important when looking at dissociation reactions, and the last includes the entropic contribution to the free energy (G = H - TS).

Optimisation of chair and boat transition structures

Optimisation of the chair transition structures (HF-3-21G level of theory)

After initial optimisation of the 'guess' of the chair transition state, with the terminal bond distances at approximately 2.2Â, the allyl fragments were then optimised using two different approaches. The first of which was to compute the force constant matrix (the Hessian), which uses the assumption that the transition state we have drawn is close to that of the real one. The alternative method is to freeze the reaction coordinate, whilst minimising the rest of the molecule, then unfreezing it. This uses the assumption that our guess transition state is not like the real one.

Use of the Hartree-Fock method, with the basis-set 3-21G, were used for both methods. The first method, calculating the Hessian, included the option 'Optimisation to a TS (Berny)' and the keywords 'Opt=NoEigen'. The job completed succesfully and the imaginary frequency of -818 cm^-1 was obtained. The animation is shown below:

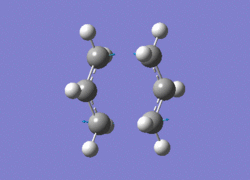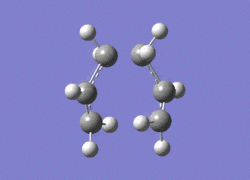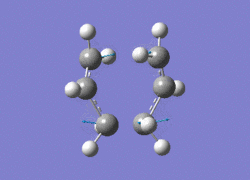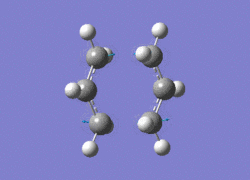
Terminal C-C lengths 2.02Â

For the alternative method this required freezing the reaction coordinates, minimising the rest of the molecule, then unfreezing the molecule and finding the transition state again. Through the use of the Coordinate Editor in Gaussview, this gave the same length as the first method (data shown above). The image below shows the confirmation of the length calculated from the frozen method:

Files showing proof of calculation:

DOI:10042/to-10182 Chair TS Non-frozen

DOI:10042/to-10183 Chair TS Frozen

Optimisation of the boat conformers with the QST2 method

Incomplete optimisation of the boat conformer

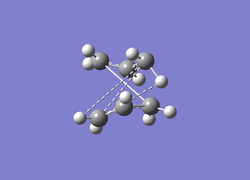
Optimisation of the boat conformer started with the use of the C_i anti2 conformer drawn in the previous section. Redrawing of the boat conformer and re-labelling of the carbon and hydrogen atoms to correspond to the two images below resulted in an incomplete optimisation. The result of which looks similar to a chair transition state but more dissociated (see thumbnail on the right).

Using the QST2 method with 'Opt+Freq' job type, the C2-C3-C4-C5 dihedral angle was changed to 0o, whilst the inside C-C-C atoms (i.e. C2-C3-C4 and C3-C4-C5 for the molecule below) were also altered to 100o. An imaginary frequency of -840 cm^-1 was obtained, as well as data on the structure of the transition state as shown:

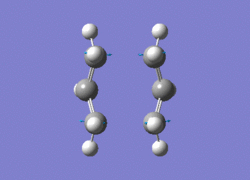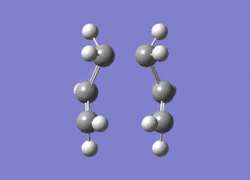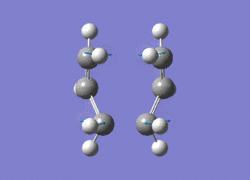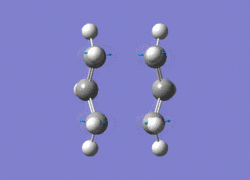
Terminal C-C lengths 2.14Â

Comparison of the two bond lengths shows the boat transition state having a slightly longer terminal C-C bond length. The energies of the boat transition states, under the various methods, is also lower than that of the chair TS (see Table 2).

File showing proof of calculation:

DOI:10042/to-10184 Boat TS QST2

The optimised chair and boat structures were then re-optimised with the DFT/B3LYP method, with the results as shown. The table below shows the results from the optimisations of both the chair and boat isomers using both methods:

Table 2: Summary of results from the optimisations of both the chair and boat conformers (Energies in Hartrees)

	HF/3-21G Method				DFT/B3LYP Method
	Electronic Energy	Sum of eletronic and zero-point energies	Sum of electronic and thermal energies	Electronic Energy	Sum of eletronic and zero-point energies	Sum of electronic and thermal energies
		At 0K	At 298.15K		At 0K	At 298.15K
Chair TS	-231.61932	-231.466702	-231.461343	-234.50547	-234.358575	-234.352235
Boat TS	-231.60280	-231.450929	-231.445301	-234.49291	-234.346091	-234.340298
Reactant (anti2)	-231.69254	-231.539539	-231.532566	-234.55970	-234.41625	-234.40895

Comparison of Table 2 to Appendix 2 shows fairly accurate results when it comes to the HF data. For the DFT method, slight discrepancies are shown, which could be due to inaccurate submission of the calculation files to the HPC centre.

Table 3 therefore uses the information from Table 2 to calculate the activation energies. The reactant is assumed to be the anti 2 conformation, so the energies for the transition states are subtracted from the reactant energy, then converted into kcal/mol from Hartrees (1 hartree = 627.509 kcal/mol)

Table 3: Summary of activation energies (kcal/mol)

	HF/3-21G (0K)	HF/3-21G (298.15K)	DFT/B3LYP (0K)	DFT/B3LYP (298.15K)	Experimental (0K)
Chair TS	45.70	44.69	36.19	35.59	33.5 ± 0.5
Boat TS	55.60	54.76	44.03	43.08	44.7 ± 2.0

Comparison of the values show that the DFT method at 0K is relatively close to the experimental values.

Files showing proof of calculation:

DOI:10042/to-10196 B3LYP Chair TS Non-Frozen

DOI:10042/to-10197 B3LYP Chair TS Frozen

Media: BOAT OPT B3LYP FREQ.LOG B3LYP Boat TS

IRC

Calculations of the energies alone is not enough to define which conformer the reaction paths from the transitions structures will lead to. However, a method called the Intrinisic Reaction Coordinate (IRC) in Gaussian shows visually where the minimum point on a potential energy surface can be.

Different calculations were carried out for both transition states. The first set calculation included computing the reaction coordinate only in the forward direction, rather than in both directions. The force constants were calculated once, reading the results from a .chk file and finally the number of steps taken along the IRC in the forward direction was changed to 50 steps.

This first calculation resulted in an incomplete result, as seen in Table 4 below. Therefore the IRC conditions were altered in order to obtain a more accurate result. The second calculation was altered to taking 75 steps, with all other factors remaining the same. This also resulted in an incomplete result, despite the curve attempting to reach a minimum point by plateauing. Finally, the last calculation was altered to 80 steps, whilst computing the force constants at every step. This is seen in Table 4, for both transition states, with the plot showing a plateau being reached. This plateau indicates that a minimum point in the potential energy surface had been found, as no energy was input to alter the reaction coordinate.

Table 4: IRC results

	IRC = 50	IRC = 80
Chair TS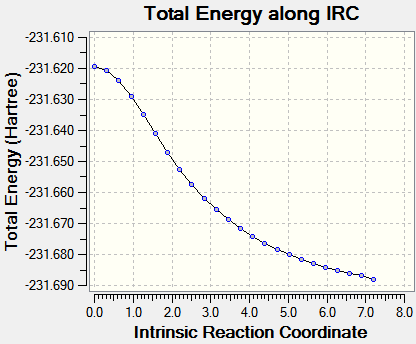
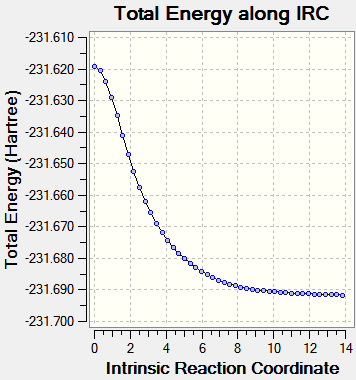Boat TS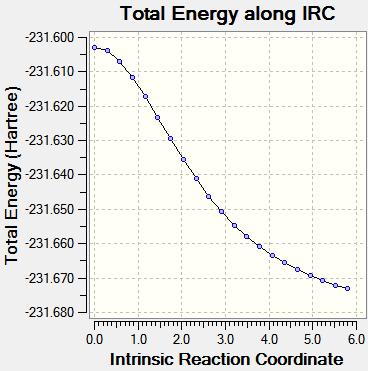

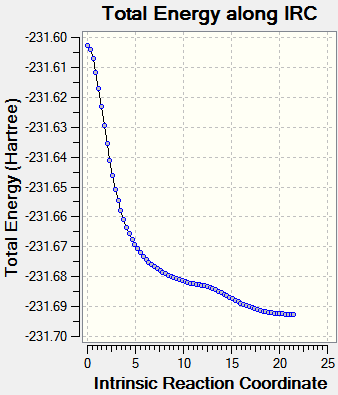The table below shows the images of the transition states after each IRC calculation:

Table: IRC images

	IRC = 50 steps	IRC = 75 steps	IRC = 80 steps, force constant recalculated
Chair TS
Boat TS		File shows the same image as the Chair TS from IRC = 50 steps

A key point from the analysis of the IRC molecules shows that both the molecules which were obtained after full minimisation are very similar to that of the gauche 3 conformer. This further confirms the theory, as shown by the energy calculations, that the gauche 3 conformer should have been the one to form during the reaction.

Files showing proof of calculation:

DOI:10042/to-10185 IRC Chair TS (50)

DOI:10042/to-10187 IRC Chair TS (75)

DOI:10042/to-10188 IRC Chair TS (80)

DOI:10042/to-10190 IRC Boat TS (50)

DOI:10042/to-10191 IRC Boat TS (75)

DOI:10042/to-10195 IRC Boat TS (80)

Diels Alder Reaction

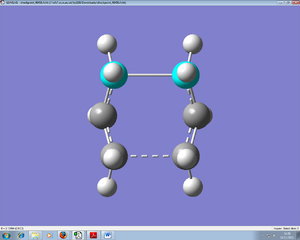
The Diels-Alder reaction comprises of a cycloaddition reaction between conjugated diene and a (possibly substituted) alkene, also known as the dienophile. This forms a cyclohexene system, as shown in the figure below. This section of the module deals with transition states, using the methods discussed in the previous section, to determine more about the reaction path and the path it decides to undergo to ensure completion.

Figure: Diels-Alder cycloaddition reaction

Cis-butadiene

First with HF method (basis-set 3-21G), then with the semi-empirical AM1 method, the cis-butadiene molecule was optimised to give the MOs (HOMO and LUMO) as seen in the Figures below:

HOMO of the cis-butadiene

LUMO of the cis-butadiene

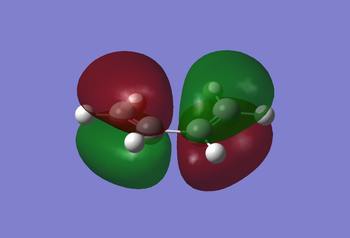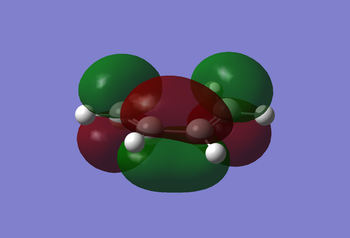The HOMO of the cis-butadiene is antisymmetric to the reflection plane (plane perpendicular to C-C/C=C bonds), whilst the LUMO is symmetric to the plane. This can be of use in the next section dealing with the transition state, when analysing why the reaction is considered 'allowed' rather than 'forbidden'.

Media: OPT CIS-BUTADIENE AM1.LOG

Diels Alder Transition State

Examination of the reaction path requires looking at the transition states. An ethylene molecule was added to the cis-butadiene molecule window after first undergoing Hartree-Fock, then semi-empirical AM1 optimisation. Then using the methods previously discussed for determining a transition state, i.e. the frozen and non-frozen methods, they obtained the MOs shown below. The non-frozen method used a semi-empirical AM1 method, with an 'Opt+Freq' job type, 'Optimisation to a TS (Berny)' and the keyword 'Opt=NoEigen'. This gave the frequencies seen below (c.f. Frequency Analysis table) and the MOs as also seen below.

HOMO of the ethylene

LUMO of the ethylene

HOMO of the transition state

LUMO of the transition state

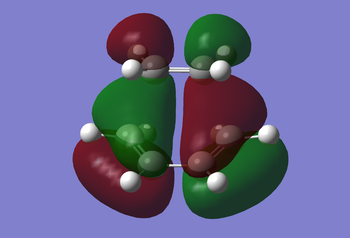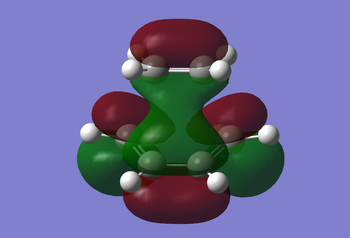Analysis of the MOs can tell us why this reaction is 'allowed' to occur. The ethylene MOs shows the HOMO being symmetric to the reflection plane, whilst the LUMO is antisymmetric with respect to the plane. Both symmetric orbitals include the HOMO of ethylene and the LUMO of butadiene, whilst the antisymmetric orbitals include the HOMO of the butadiene and the LUMO of the ethylene. Therefore this reaction is allowed due to sufficient orbital overlap interaction of the HOMO-LUMO pairs of ethylene and butadiene.

The HOMO of the transition state can be considered anti-symmetric with respect to the reflection plane, so the LUMO can be considered symmetric.

Now looking at the geometry and structure of the transition state, normally the van der Waal's radius of the carbon atom is considered to be 1.7Â, whilst the normal sp² C-C bond length is 1.34Â, the sp³ C-C bond length is 1.54Â.. The values from the transition state show C=C sp² bond lengths to be 1.38Â, whilst the C-C sp³ bond length is 1.40Â. The distance between the two reactants is now 2.12Â.

What this tells us is that, since the sp² and sp³ bondlengths are different to the experimental values, the lengths in the transition state are somewhere between forming single and double bonds. The partly formed bond length at 2.12Â tells us that, since this value is more than an expected C-C σ bond length but less than two van der Waals radii worth, the transition states have not necessarily formed a C-C σ bond but experiences van der Waals interactions.

Frequency Analysis of the Transition State

Frequency	Animation (click on image)	Wavenumber (cm-1)
Imaginary		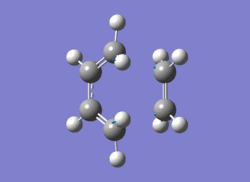-956.30
Lowest positive		147.22

Now analysis of the vibrations can determine whether the bonds are synchronous or asynchronous. The animation for the negative frequency shows a stretching frequency with the bonds forming at the same time, indicating synchronous bonds. The next frequency it can be compared to, the lowest positive one, shows a bending frequency indicating asynchronous bonds.

Media: OPT ETHYLENE AM1.LOG Optimisation Ethylene (AM1)

Media: OPTFREQ CIS-BUT ETH TS BERNYAM1.LOG Opt+Freq Butadiene and Ethylene TS (AM1)

The Regioselectivity of the Diels-Alder reaction

This Diels-Alder reaction deals with cyclohexa-1,3-diene reacting maleic anhydride to form two products, one endo form and one exo. The endo form (the product in the image on the bottom) is the favoured product, provided kinetic control is the overriding method. Through analysis of the transition states, we can determine the reasons why the endo form is favoured.

Diels Alder reaction of Cyclohexa-1,3-diene with Maleic anhydride

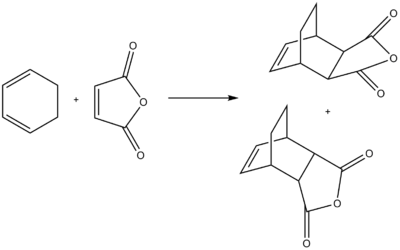
The method involved drawing each of the reactants separately, optimising them using first the HF method, then the semi-empirical AM1 method. The two reactants were then placed in one window, where the frozen method was used to carry out the calculations. Again using the Coordinate Editor in Gaussview, the bonds between the terminal ends of the C=C bonds were frozen to 2Â, before being unfrozen again (having optimised the rest of the molecule). The semi-empirical AM1 method was chosen, with the 'Opt+Freq' job type; optimising to a 'TS(Berny)'; calculating the force constants 'Always' and using the keywords 'Opt=NoEigen' to stop the program freezing after finding one imaginary frequency. The summary of results from the optimisation of both transition states are shown in Table 5 below:

Table 5: Summary of results from the optimisations of the two transition states

	Endo TS	Exo TS
Calculation Type	FREQ	FREQ
Calculation Method	RAM1	RAM1
Basis Set	ZDO	ZDO
Charge	0	0
Spin	Singlet	Singlet
E(RAM1)	-0.05150 a.u.	-0.05041 a.u.
RMS Gradient Norm	0.00000019 a.u.	0.00000069 a.u.
Dipole Moment	6.17 Debye	5.56 Debye
Imaginary Frequency Image
Imaginary Frequency (cm-1)	-806.38	-812.19

The endo form is 0.68 kcal/mol lower than the exo transition state, so the lower energy conformer is the one which forms confirming why the endo is the favoured product. The endo product has a bond forming length between the two reactants of 2.16Â, whilst the exo product has a length of 2.17Â. The slight difference in bond forming lengths can be related to slight steric repulsion between the bridgehead and the maleic anhydride, which is seen in the exo form but not in the endo.

Table: MOs of the endo and exo transition states

	Endo TS	Exo TS
HOMO
LUMO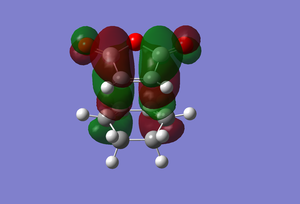

Another reason why the endo form is lower in energy can be concluded using the theory of secondary orbital overlap. As seen from the Figure above, there are two more p orbital interactions in the endo form than there is the exo, which can therefore account for the shorter distance for the endo form between the -(C=O)-O-(C=O)- fragment and the -CH=CH- (endo)/ -CH2-CH2- (exo) fragments. The endo distance is 2.89Â versus 2.95Â for the exo distance. The closer the alignment between orbitals, the stronger the orbital interaction, the closer the distances as there are favourable interactions.

Figure: Proof of bond forming lengths for endo and exo TS respectively.

Media: OPT ENDO BOND DERIV 2A AM1.LOG Optimisation of Endo TS

Media: OPTFREQ EXO BOND DERIV AM1.LOG Opt+Freq of Exo TS

Conclusion

Overall the methods used at different levels of theory have helped, through calculations of energies, to determine the difference between transition states has been successful for analytical use. The Cope Rearrangement occurs via either a chair or boat transition state, the mechanism of which is not defined. Through our methods of calculation, the gauche 3 conformer was seen to be the most stable conformer, yet the anti 2 conformer is the one preferred to be the reactant. The energies, calculated through HF and DFT methods, along with the activation energies of the reaction showed that the chair transition state is the preferred reaction path. The lower energies, relatively close to that of the experimental values, confirms this. It also showed us that the DFT/B3LYP method was more accurate in determining activation energies (at 0K).

For the Diels-Alder reaction, the analysis of the MOs were successful in analysing the reaction why the original reaction between the cis-butadiene and the ethylene can occur. Correct analysis of the symmetry of the MOs determined which HOMO-LUMO pairs reacted and therefore why the reaction was deemed to be allowed. For the endo and exo transition states from the reaction between cyclohexa-1,3-diene and maleic anhydride, the endo was considered the favoured product. This was explained due to the calculated energies and also the effect of the secondary orbital overlap, which were discussed in the section.