Rep:Mod:BTL093
Module 3: Physical Computational Chemistry
The Cope Rearrangement of 1,5 Hexadiene
Optimising the Reactants and Products
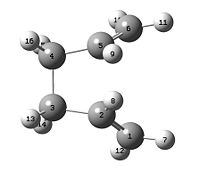
Conformers of 1,5 Hexadiene
Using Gaussview, various conformers, with gauche and anti linkage, was optimised using HF/3-21G level. The energy of these conformers was investigated.
| Conformer (naming corr. to Appendix 1) | Structure | Point Group | Energy / Hartree | Relative Energy / kcal mol-1 |
|---|---|---|---|---|
| Anti 1 | C2 | -231.69260 | 0.04 | |
| Anti 2 | Ci | -231.69254 | 0.08 | |
| Anti 4[1] | C1 | -231.69097 | 1.06 |
| Conformer (naming corr. to Appendix 1) | Structure | Point Group | Energy / Hartree | Relative Energy / kcal mol-1 |
|---|---|---|---|---|
| Gauche 1[2] | C2 | -231.68772 | 3.10 | |
| Gauche 3 | C1 | -231.69266 | 0.00 | |
| Gauche 4 | C2 | -231.69153 | 0.71 | |
| Gauche 6[3] | C1 | -231.68916 | 2.20 |
The energies and point gruops coincides with the information provided from appendix 1.
The relative energy was calculated when comparing to the lowest energy conformer by employing 1 Hartree = 627.509 kcal mol-1.
The lowest energy conformer was first thought to be anti 1 which is totally anti-periplanar, minimising the steric forces between the side groups. However, with the increase in chain length, gauche conformers are more favoured due to the increase in van der waal's interaction between the substituents. Therefore, it was thought that gauche 4 would have a low energy as it consists of a gauche main chain with anti side group, minimising steric forces and maximising favourable interactions. However, in fact, it is even higher in energy than anti 1
After further calculation, it can be seen that in fact, gauche 3 is the lowest energy conformer. This was further investigated by looking at the HOMO of the moleucle:[4]
From the HOMO of gauche 3, it can be seen that there are strong interactions among the 2 C=C pi electrons and the CH bonds. This stereoelectronic effect between the CH bonds and pi electron stablises the conformer.
Optimising the Anti 2 structure using higher level method
The Anti 2 structure was investigated further using a higher level calculation method, B3LYP/6-31G. The two methods were compared in terms of energy and geometry
| HF/3-21G | B3LYP/6-31G | |
|---|---|---|
| Energy / Hartree | -231.69254 | -234.61171 |
| Point Group | Ci | Ci |
| HF/3-21G | B3LYP/6-31G | |
|---|---|---|
| 1,2,6,9 | 114.7o | 118.6o |
| 6,9,12,13 | -114.7o | -118.6o |
| HF/3-21G | B3LYP/6-31G | |
|---|---|---|
| 1-2 & 12-13 / Å | 1.32 | 1.33 |
| 2-6 & 9-12 / Å' | 1.51 | 1.51 |
| 6-9 / Å | 1.55 | 1.55 |
I can be observed that with a higher level optimisation, the energy is reduced. The geormetries are similar with point group and bond length remain unchanged. The major deviation was accounted for the dihedral angle with are larger value obtained using B3LYP/6-31G. The dihedral angle in the backbone remains unchange, being anti-periplanar with an angle of 180, but the dihedral angle between the ethylene group and the central carbon linkage was increased. This relief in strain might contribute to the reduction in the total energy.[5]
Frequency analysis and Thermal Energies of Anti 2 conformer
Frequency analysis was done to confirm that the structure obtained from optimisation is the ground state instead of the transition state. With the transition state, an imaginary frequency will be obtained, while in ground state, all frequencies obtained will be positive.
No negative frequencies was obtained, thus the structure optimised was the ground state.
Some of the major frequencies were listed below:
| Vibration Mode | Form of vibration | Frequency / cm-1 | Intensity |
|---|---|---|---|
| 1 | C-H Bend | 670 | 20 |
| 2 | C-H Bend | 938 | 13 |
| 3 | C-H Bend | 940 | 61 |
| 4 | C-H Bend | 1036 | 20 |
| 5 | C=C Stretch | 1734 | 18 |
| 6 | Symmetric C-H Stretch | 3031 | 54 |
| 7 | Asymmetric C-H Stretch | 3080 | 36 |
| 8 | C-H Stretch | 3137 | 56 |
| 9 | Symmetric C-H Stretch | 3155 | 14 |
| 10 | Asymmetric C-H Stretch | 3234 | 45 |
The thermal energies of the anti 2 conformers was also calculated along side with the frequencies. The thermal energy of the structure at 298.15K and 0.00 K was compared:
| 298.15K | 0.00K | |
|---|---|---|
| Sum of electronic and zero-point energies / Hartrees | -234.469204 | -234.468766 |
| Sum of electronic and thermal energies / Hartrees | -234.461857 | -234.468766 |
| Sum of electronic and thermal enthalpies / Hartrees | -234.460913 | -234.468766 |
| Sum of electronic and thermal free energies / Hartrees | -234.500777 | -234.468766 |
At 0K as no vibrations occur, the 4 energies are equal. At higher temperature, the absorption of thermal energy will affect the sum of the electronic energy and the various thermal energies. This can be observed from the sum of electronic energy and zero-point energy where in 298.15K the value is smallerthan that in 0.00K.[6]
Optimising the Chair and Boat Transition states
Chair Transition State
Optimising the Chair TS using 2 different method
The chair transition state can be optimised directly to the TS using the Berny method or by first freezing the coordinate using the Redundant coordinate followed by optimisation.
| Berny Method[7] | Redundant Coordinate Method[8][9] | |
|---|---|---|
| Energy / Hartree | -231.61932 | -231.61932 |
| Bond forming/braking Bond Length / Å | 2.02 | 2.02 |
| Imaginary Frequency / cm-1 | -818 | -818 |
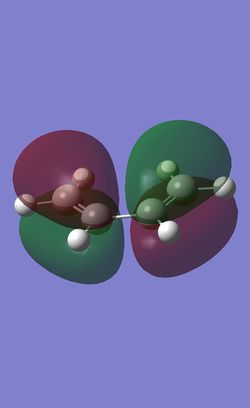
| Vibration Mode | 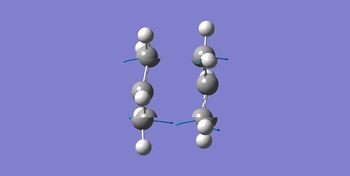 |
|
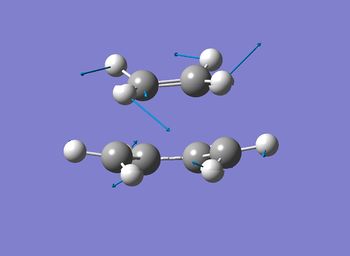
Identical results were obtained showing that the two methods coincides with each other when solving this particular problem. One imaginary frequency was obtained confirming that the structures obtained were transition state. That frequency obtained shows simultaneous, concerted formation and breakage of the bond as seen in the graph above. This coincides with the concerted fashion of the Cope Rearrangement.
Intrinsic Reaction Coordinate of the Chair Transition State
The vibration mode provides clue on how the bonds were formed, but it is not sufficient to predict the product from that particular transition state. By convergence, the IRC will allow the calculation of the product by looking at the potential surface from the transition state.
In this experiment, 50 points along the IRC was used. The calculation was done twice, first time with force constant calculated once and the second with force constant calculated always.
Force constant calculated once[10]
Energy: -231.619322 Hartree
The structure of product:
24 Steps were done to get to product.
Force constant calculated always[11]
Energy of product: -231.691648 Hartree
The structure of product:
47 Steps were done to get to product.
From the above it can be seen that with force constant calculated always, more steps were done to get to the ground state. Force constant calculated always gives a more accurate result. This can be observed from the lower energy of the structure, a gradient towards 0. The gradient was used to find the ground state from the potential surface as the minimum point on the graph will have a gradient of zero. From the IRC, the structure of the product from the chair transition state can be visualised. From the structure and the energy of the structure, it can then be found it is very similar to gauche 2 (naming corr. to appendix 1) which might be the possible product from the chair transition state. Further investigation must to done to confirm this.
Boat Transition State
By optimising the intramolecular rearrangement of Anti 2, where the diehedral angle of the central carbon linkage was set to 0 and the angles between the carbon linkage and the C=C were set to 100 for both product and reactant as seen below. The optimisation of the two molecule to the transition state employing the QST2 method allow us to visualise the chair transition state.
The product and reactants:
| Reactant | Product |
| Boat Transition State[13] | |
|---|---|
| Energy / Hartree | -231.602802 |
| Bond forming/braking Bond Length / Å | 2.14 |
| Imaginary Frequency / cm-1 | -840 |
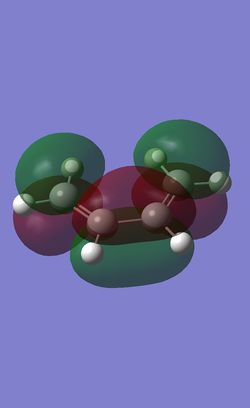
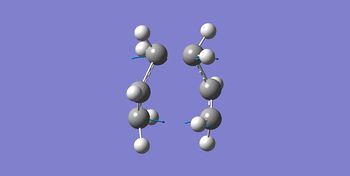
| Vibration Mode | 
|
Only one imaginary frequency was observed, indicating the validity of the structure to be a transition state. The mode of the vibration also shows subsequent formation and breakage of the bond to form and dissociate with the anti 2 conformer. This also coincided with the concerted mechanism of the [3,3]-sigmatropic Cope Rearrangement.
Activation Energy when comparing the 2 transition states to Anti 2 Conformer
After calculating the frequencies at 0.001K and 298.15K using the HF/3-21G and B3LYP/6-31G method for both transition state and the anit 2 conformer, the activation energy at both temperature can be calculated.
| Electronic Energy / Hartree | Sum of Elctronic and Zero-point Energies at 0 K / Hartree | Sum of Electronic and Thermal Energies at 298.15 K / Hartree | ΔEa at 0 K / Hartree | ΔEa at 298.15 K / Hartrees | ΔEa at 0 K / kcal mol-1 | ΔEa at 298.15 K / kcal mol-1 | Expt. ΔEa at 0 K / kcal mol-1 | |
| Anti 2 Reactant[14] | -231.692535 | -231.539070 | -231.532565 | n/a | n/a | n/a | n/a | n/a |
| Chair | -231.619322 | -231.466696 | -231.461337 | 0.072374 | 0.071228 | 45.42 | 44.70 | 33.5 ± 0.5 |
| Boat | -231.602802 | -231.450930 | -231.445301 | 0.08814 | 0.087264 | 55.31 | 54.76 | 44.7 ± 2.0 |
| Electronic Energy / Hartree | Sum of Elctronic and Zero-point Energies at 0 K / Hartree | Sum of Electronic and Thermal Energies at 298.15 K / Hartree | ΔEa at 0 K / Hartree | ΔEa at 298.15 K / Hartrees | ΔEa at 0 K / kcal mol-1 | ΔEa at 298.15 K / kcal mol-1 | Expt. ΔEa at 0 K / kcal mol-1 | |
| Anti 2 Reactant | -234.611710 | -234.468766 | -234.461857 | n/a | n/a | n/a | n/a | n/a |
| Chair[15][16] | -234.558854 | -234.414482 | -234.409092 | 0.054284 | 0.052765 | 34.06 | 33.11 | 33.5 ± 0.5 |
| Boat[17][18] | -234.543093 | -234.401901 | -234.396006 | 0.066865 | 0.065851 | 41.95 | 41.32 | 44.7 ± 2.0 |
1 Hartree = 627.509 kcal mol-1.
ΔEa at 0K corresponds to the differences between the sum of electronic and zero-point energy when comparing the transition states to the reactant while for ΔEa at 298.15K is that between the sum of electronic and thermal energies.
It can be found that the chair has a lower activation energy. This coincides with the total energy of the structures which indicate that the chair transition state is the more stable transition state. This is due to steric factors as in boat, groups eclipse to each other leading to large steric repulsion which causes the structure to be higher in energy while in chair the staggered conformation minimises the steric repulsion.
With a higher level basis set used in B3LYP/6-31G it can be seen that the calculated values are in generally small but more accurate and in better agreement with the experimental literature values. With the HF.3-21G the values are larger and deviated more when compared to the experimental values. With the better agreement with the experimental value it can be evaluated B3LYP allows more accurate activation energy calculation.
Diels-Alder Reaction Analysis
Diels-Alder Reaction between cis-butadiene and ethlyene
Molecular Orbitals of the reactants
To better understand the reaction, the HOMO and LUMO of the reactants, cis-butadiene and ethlyene were investigated.
The reactants were optimised with semi-empirical AM1 method and the MOs were plot.
Orbitals of same symmetric interacts strongly. Therefore, it can be predicted that the HOMO of ethlyene will interact strongly with the LUMO of cis-butadiene, while the HOMO of cis-butadiene will interact strongly with the LUMO of ethlyene. The small difference in the energies between the HOMO and LUMOs also give rise to good orbital overlapping. These will allow the prediction of the [4+2] Cycloaddition to form a ring.
Structure and Molecular Orbitals of Transition State
Optimising the Transition State
The reductant coordinate method was employed to optimised the transition state of the reaction of cis-butadiene and ethlyene. This method allows better convergence to the maximum point by first optimising to a freeze coordinate then optimise towards the transition state. The optimisation will be more accurate than the Berny method to directly optimise to the transition state.
In the below optimisation, the distance between the carbons where the bonds were to form was frozen to 2.2Å. The structure was first optimised to the minimum under the freeze coordinate then optimised to its corresponding transition state using semi-empirical AM1 method.
Frequency Analysis was done after the optimisation to confirm that the structure obtained is the transition state.
| cis-Butadiene and Ethlyene Transition State[19] | |
|---|---|
| Energy / Hartree | 0.11166 |
| Bond forming/braking Bond Length / Å | 2.12 |
| Imaginary Frequency / cm-1 | -957 |
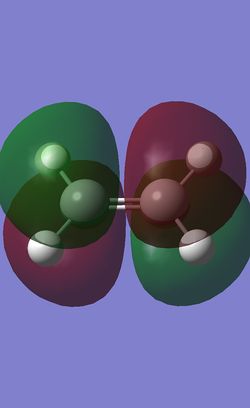
| Vibration Mode | 
|
Only one imaginary frquency at -957 cm-1 was observed indicating the validity of the structure to be a transition state. The vibration mode shows the shows the synchronous formation of the bond which occurs between the terminal carbons and the ethylene where the carbons come towards each other during the vibration.
The lowest positive frquency occurs at 145cm-1 which has a low internsity. The vibration mode of the frequency is showed below.
The vibration is the bending of C-H bonds and does not indicate any forming and breaking of bonds.
Molecular Orbitals of the Transition State
After confirming the structure of the transition state, the HOMO and LUMO of the transition state were investigated.
| Transition State | |
|---|---|
| HOMO | 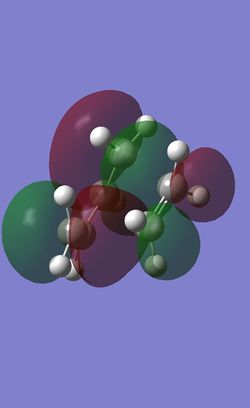
|
| HOMO Symmetry | anti-symmetric |
| HOMO Energy | -0.32378 |
| LUMO | 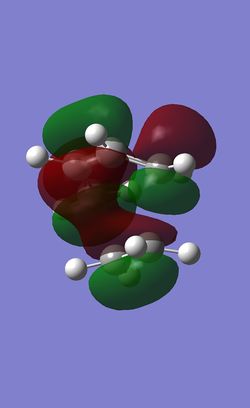
|
| LUMO Symmetry | symmetric |
| LUMO Energy | 0.02308 |
The HOMO of the transition state is anti-symmetric. The symmetry and the shape of the electron density indicates that the HOMO of the transition state is the combination of the HOMO of cis-butadiene and LUMO of ethlyene which are both anti-symmetric. The overlap of these two orbitals forms 2 new bonds under a concerted [4+2] Cycloaddition leading to a typical Diels-Alder Reaction.
The LUMO is symmetric and was the combination of the LUMO of cis-butadiene and the HOMO of ethlyene.
Structural Properties of the Transition State
The geometry of the transition state is differs when using different method.
| HF/3-21G | B3LYP/6-31G | |
|---|---|---|
| 1-2-3 & 1-2-4 | 121.2o | 122.0o |
| 2-1-5 & 3-4-6 | 99.5o | 102.3o |
| HF/3-21G | B3LYP/6-31G | |
|---|---|---|
| 1-2 & 3-4 / Å | 1.38 | 1.38 |
| 2-3 / Å' | 1.40 | 1.40 |
| 5-6 / Å | 1.38 | 1.39 |
| Bond Forming/Breaking Bond Legnth 1-5 & 4-6 / Å | 2.12 | 2.27 |
In terms of the bond lengths, apart from the bond forming/braking bond length, which increases when using a higher level method, the two method coincides with each other especially when looking at the bond length within the cis-butadiene fragment. The bond angles within in the cis-butadiene changes slightly but a significant increase in bond angle was found for the angle between the two fragments. This shows that with a higher level used, the location of the ethylene fragment from the cis-butadiene changes.
A typical sp2 C=C and sp3 C-C bond is 1.48Å and 1.54Å[20] respectively. The bond lengths in the transition state are smaller than its corresponding typical values. This is because bond 2-3 was in the transition to form a C=C while the molecule was in the transition of forming a ring structure via concerted cycloaddition. The van der Waals radius of the C atom is 1.70Å[21]. In both calculation, the bond forming/breaking bond length is smaller than 2 carbon atoms, showing that it was under some favourable interactions, pulling the atoms together. It shows that a bond is forming between the atoms.
Activation Energy calculated with different methods
The activation energy was calculated using the semi-empirical method AM1 method and the B3LYP/6-31G method at 0K and 298.15K.
| Electronic Energy / Hartree | Sum of Elctronic and Zero-point Energies at 0 K / Hartree | Sum of Electronic and Thermal Energies at 298.15 K / Hartree | ΔEa at 0 K / Hartree | ΔEa at 298.15 K / Hartrees | ΔEa at 0 K / kcal mol-1 | ΔEa at 298.15 K / kcal mol-1 | Expt. ΔEa at 0 K / kcal mol-1 | |
| cis-butadiene | 0.04878 | 0.134808[22] | 0.138574[23] | n/a | n/a | n/a | n/a | n/a |
| Ethylene | 0.02619 | 0.077365[24] | 0.080254[25] | n/a | n/a | n/a | n/a | n/a |
| TS | 0.11166 | 0.253712[26] | 0.259461[27] | 0.041539 | 0.040633 | 26.1 | 25.5 | 27.5 ± 1.2[28] |
| Electronic Energy / Hartree | Sum of Elctronic and Zero-point Energies at 0 K / Hartree | Sum of Electronic and Thermal Energies at 298.15 K / Hartree | ΔEa at 0 K / Hartree | ΔEa at 298.15 K / Hartrees | ΔEa at 0 K / kcal mol-1 | ΔEa at 298.15 K / kcal mol-1 | Expt. ΔEa at 0 K / kcal mol-1 | |
| cis-butadiene | -155.98434 | -155.898896[29] | -155.894603[30] | n/a | n/a | n/a | n/a | n/a |
| Ethylene | -78.58746[31] | -78.536052[32] | -78.533177 | n/a | n/a | n/a | n/a | n/a |
| TS | -234.54390[33] | -234.402886[34] | -234.396907 | 0.032062 | 0.030873 | 20.1 | 19.4 | 27.5 ± 1.2 |
It can be seen that with the semi-empirical AM1 method, the activation obtained is only slightly lower than the range of the literature value. It is therefore in good agreement with the literature. Using the B3LYP/6-31G method, the activation energy obtained is smaller and does not coincide with experimental value. Therefore it can be seen that semi-empirical methods are more applicable in this situation as it takes into account the quantum mechanics of the Huckel transition state. This experiment could be improved by using higher level method such as the PM6 method.
Regioselectivity of the Diels-Alder Reaction
Optimisation of the exo and endo Transition State
The transition states were optimised using the redunctant coordinate method. The bond forming/breaking bond length was first frozen to 2.2Å and was minimised to a minimum. The optimised structure was then optimised to the transition state.
| exo[35] | endo[36] | |
|---|---|---|
| Energy / Hartree | -0.05042 | -0.05151 |
| Bond forming/braking Bond Length / Å | 2.17 | 2.16 |
| Imaginary Frequency / cm-1 | -812 | -806 |
| Vibration Mode |  |
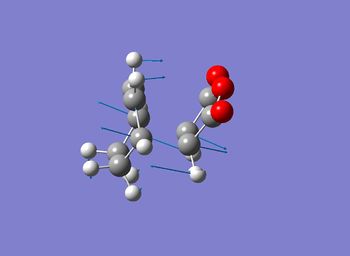
|
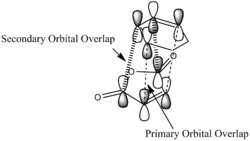
One imaginary frequency was found for both structure confirming that both are transition state structures. The vibration mode indicates the synchronous formation of the 2 bonds showing that the reaction is under a concerted mechanism. The frequency of the vibrations also differ due to the change of the location of the maleic anhydride. The lower magnitude in the imaginary vibration mode in the endo transition state is due to the stablisation via a secondary orbital overlaps.
It can be seen that the Endo transition state is lower in energy when comparing to the exo transition state. This coincided with the fact that this reaction is under kinetic control where the endo transition state is lower in energy and that the endo product is the kinetic product.
Molecular Orbital of the exo and endo Transition States
| exo[37] | endo[38] | |
|---|---|---|
| HOMO |  |

|
| HOMO Symmetry | anti-symmetric | anti-symmetric |
| HOMO Energy | -0.34274 | -0.34505 |
| LUMO | 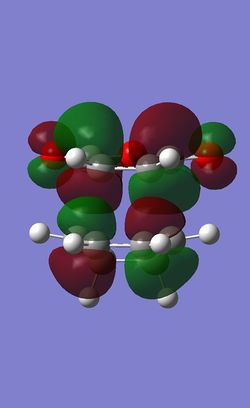 |

|
| LUMO Symmetry | anti-symmetric | anti-symmetric |
| LUMO Energy | -0.04046 | -0.03571 |
The frontier orbitals of the exo and endo tranisition states are all antisymmetric. It can be observed in both HOMOs that there are primary orbital overlap between C1, C4 in 1,3 cyclohexadiene and the C=C carbons in maleic anhydride, which leads to bond formations between the atoms in the maleic anhydride and the cyclohexadiene in a concerted mechanism.
The HOMO of the transition state is also slightly in lower in energy. This coincides with the fact that exo product is the kinetic product of the reaction.
Further investigation was done by comparing the HOMO and LUMO to the frontier orbitals of the reactants.
| 1,3 Cyclohexadiene[39] | Maleic Anhydride[40] | |
|---|---|---|
| Energy / Hartree | 0.02771 | -0.12182 |
| HOMO |  |
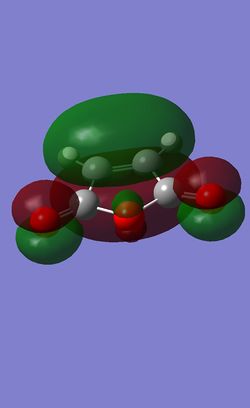
|
| HOMO Symmetry | anti-symmetric | symmetric |
| HOMO Energy | -0.32194 | -0.44187 |
| LUMO |  |
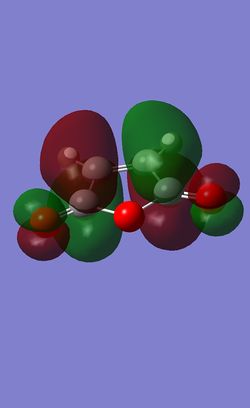
|
| LUMO Symmetry | symmetric | anti-symmetric |
| LUMO Energy | -0.01680 | -0.05949 |
It can now be seen that the HOMO of both transition states are the results of the interaction of the HOMO of Cyclohexadiene and the LUMO of the Maleic Anhydride. The Exo transition state HOMO is the combination of the HOMO of Cyclohexadiene and the LUMO of the Maleic Anhydride while for the HOMO of the endo TS, it is the HOMO of the cyclohexadiene and the negative version of the LUMO of Maleic Anhydride, where the wavefunctions are swapped round, with the positive orbitals now negative and vice versa. The small energy gap between the HOMO and LUMO in the reactant give rise to these interactions, alongside with the same symmetry, they interact favourably.
Secondary Orbital Overlap
The endo transition state was known to have lower energy transition state leading to a kinetic control of the Diels-Alder Reaction of the Cyclohexadiene and the Maleic Anhydride to prefer the endo product. This is due to secondary orbital overlaps between the cyclohexadiene and the maleic anhydride which a sample can be observed from the LUMO+1 of the transition states.
| Exo | Endo | |
|---|---|---|
| LUMO+1 |  |

|
| LUMO+1 Symmetry | symmetric | anti-symmetric |
| LUMO+1 Energy | -0.02012 | -0.02013 |
In the endo transition state secondary orbital overlap occurs between the p orbitals -CH=CH- in cyclohexadiene -(C=O)-O-(C=O)- in maleic anhydride as the orbitals were in same phase while in the exo transitino state, the secondary orbitals are largely stretches as seen in the LUMO+1 above and the interaction is thus not favourable. In the HOMO of the exo transition state, it can be found that the -CH=CH- in cyclohexadiene -(C=O)-O-(C=O)- in maleic anhydride are far apart and no interaction can be observed.
This secondary overlapping of orbitals in endo transition state stablises the structure and thus leads to the kinetic control of the reaction to kinetically favour the endo product due to a lower activation energy required.
The secondary orbital overlap was not confirmed using the optimisation of the HOMO of the endo TS. However, this can be confirmed by calculating the distance between -CH=CH- in cyclohexadiene -(C=O)-O-(C=O)- in maleic anhydride.
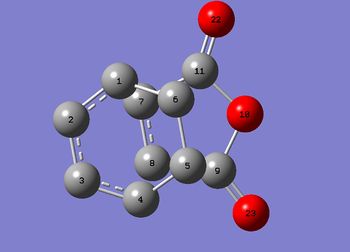
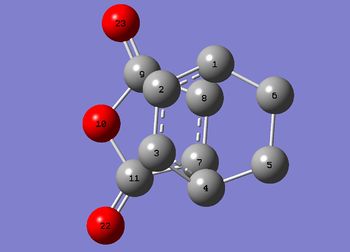
Structural Analysis of the exo and endo Transition States
| Exo | Endo |
| Exo | Endo | |
|---|---|---|
| 3-4-5 & 2-1-6 | 120.0o | 120.0o |
| Exo | Endo | |
|---|---|---|
| 1-2 & 3-4 / Å | 1.39 | 1.39 |
| 1-6 & 4-5 / Å' | 1.49 | 1.49 |
| 2-3 / Å | 1.40 | 1.40 |
| 5-6 / Å | 1.52 | 1.52 |
| 7-8 / Å | 1.41 | 1.41 |
| 8-9 & 7-11 / Å | 1.49 | 1.49 |
| 9-10 & 10-11 / Å | 1.41 | 1.41 |
| Bond Breaking/Forming Bond Length 1-7 & 4-8 / Å | 2.17 | 2.16 |
| Secondary Overlapping Bond Length 1-7 & 4-8 / Å | 3.78 | 2.89 |
The structural difference in the TS is only accounted when measuring the location of one fragment in relative to the other. It can be found that the distance between 1-7 and 4-8 is a lot smaller in endo which is 2.89Å. As mentioned before, the van der waal's radius of a carbon atom is 1.70Å, a length of 2.89Å indicates interaction between the atoms and this coincides with the secondary orbital overlapping predicted in the MO analysis. The bond breaking/forming bond length in endo is also reduced. This is largely due to effect of the secondary overlapping of orbitals and the steric clashing between 6-11 and 5-9 which both accounts for a distnace of 2.94Å in the exo TS which does not occur in the endo transition state
Intrinsic Reaction Coordinate
IRC was calculated for both exo and endo transition state with 100 steps in both directions and force constant calculated always.
| Exo[41] | Endo[42] | |
|---|---|---|
| Reactant Structure | ||
| Bond forming/braking Bond Length / Å | 4.71 | 4.49 |
| Product Structure | ||
| Energy / Hartree | -0.15991 | -0.16017 |
| New Bond Length Formed from TS / Å | 1.54 | 1.54 |
| Steps Reactant to Product | 110 | 124 |
| Final R.M.S Gradient Towards Reactant | 0.00002393 | 0.00001113 |
| Overall IRC Graph | 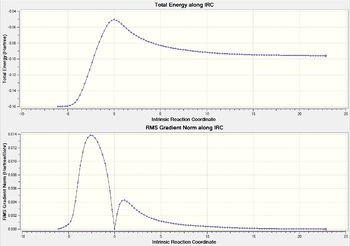 |
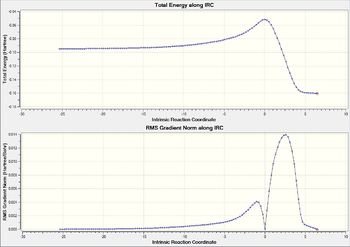
|
The above table shows the change from reactants to products. The products from each transition state was also predicted with the optimised energy and the length of the new bond formed.
It can be found that the IRC graphs for the exo and endo transition states are mirror images of each other. In endo the product lies towards the right while the reactants to the left. In exo transition state, it was the other way round.
The endo product was also found to have lower energy, thus is the more stable product. It can thus found that in this reactions, the kinetic product which has the lower transition state is also the thermodynamic product which has a lower energy.
Visualising the change from reactant to product can be done by referring to the references.
Effects that have been neglected in the calculations of Diels Alder TS
Some limitations have been discovered during these calculations. The accuracy and the value of the result depend largely on the method employed. With different methods, different parameters were used, for example, semi-empirical method has a better look at quantum mechanic effects while DFT does. Results obtained thus vary and can be seen in the calculation of the 1,5 hexadiene. Using HF/3-21G the most stable conformer is gauche 3, while using DFT B3LYP/6-31G, anti 1 is the most stable conformer. Therefore, to better improve the calculation, a better knowledge of the calculation method should be obtained in order to choose the most appropriate method. Larger basis set should also be used to improve the calculation
In the calculation of the Diels-Alder reactions, which is a pericyclic reaction, the effect of a light activation, which can form a Mobius or Huckel transition state in different conditions, was not taken into account in the calculations. The solvent effects on the reactions was also neglected. solvents of different polarity can interact with the polar groups in the reactant in different extent and thus affecting the reactions. In the calculation, it was not able to predict whether the reaction is under thermodynamic or kinetic control unless a known product was specified.
References
- ↑ Anti 4 Optimisation DOI:10042/to-11303
- ↑ Gauche 1 OptimisationDOI:10042/to-11305
- ↑ Gauche 6 OptimisationDOI:10042/to-11304
- ↑ Gauche 3 MO calculation DOI:10042/to-11308
- ↑ Anti 2 B3LYP 6-31G Optimisation DOI:10042/to-11306
- ↑ Anti 2 B3LYP 6-31G Frequency Calculation DOI:10042/to-11307
- ↑ Chair Berny optimisation DOI:10042/to-11533
- ↑ Chair Redundant 1st optimisation DOI:10042/to-11531
- ↑ Chair Redundant final optimisation DOI:10042/to-11532
- ↑ IRC Force Constant Once for Chair transition state DOI:10042/to-11528
- ↑ IRC Force Constant Always for Chair transition state DOI:10042/to-11529
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3
- ↑ Boat Transition State Optimisation+Freq after angle adjustment HF/3-21G DOI:10042/to-11530
- ↑ Anti 2 HF/3-31G Frequency Calcultion at 0K DOI:10042/to-11389
- ↑ Chair B3LYP/6-31G Frequency Calcultion at 298.15K DOI:10042/to-11385
- ↑ Chair B3LYP/6-31G Frequency Calcultion at 0K DOI:10042/to-11386
- ↑ Boat B3LYP/6-31G Frequency Calcultion at 298.15K DOI:10042/to-11387
- ↑ Boat B3LYP/6-31G Frequency Calcultion at 0K DOI:10042/to-11388
- ↑ Transition State optimisation and MO calculation DOI:10042/to-11527
- ↑ F. Allen, O. Kennard, L. Brammer, A. Orpen, J. Chem. Soc., Perkin Trans., 2, 1987, S1-S19 DOI:10.1039/P298700000S1
- ↑ A. Bondi, J. Phys. Chem., 1964, 440-442 DOI:10.1021/j100785a001
- ↑ cis-butadiene Opt+Freq AM1 0K Calculation DOI:10042/to-11510
- ↑ cis-butadiene Freq AM1 298.15K Calculation DOI:10042/to-11520
- ↑ Ethylene Opt+Freq AM1 0K Calculation DOI:10042/to-11514
- ↑ Ethylene Freq AM1 298.15K Calculation DOI:10042/to-11522
- ↑ Transition State Opt+Freq AM1 0K Calculation DOI:10042/to-11516
- ↑ Transition State Opt+Freq AM1 298.15K Calculation DOI:10042/to-11516
- ↑ V. Guner, K. Khuong, A. Leach, P. Lee, M. Bartberger, K. Houk, J. Phys. Chem., 2003, 107, 11445-11459 DOI:10.1021/jp035501w
- ↑ Ethylene Opt+Freq 0K B3LYP/6-31G Calculation DOI:10042/to-11501
- ↑ cis-Butadiene Opt+Freq B3LYP/6-31G 298.15K Calculation DOI:10042/to-11505
- ↑ Ethylene Opt+Freq B3LYP/6-31G 298.15K Calculation DOI:10042/to-11504
- ↑ Ethylene Opt+Freq 0K B3LYP/6-31G Calculation DOI:10042/to-11499
- ↑ Transition State Opt+Freq B3LYP/6-31G 298.15K Calculation DOI:10042/to-11502
- ↑ Transition State Opt+Freq B3LYP/6-31G 0K Calculation DOI:10042/to-11497
- ↑ Exo Freeze Coordinate Optimisation DOI:10042/to-11490
- ↑ Endo Freeze Coordinate Optimisation DOI:10042/to-11487
- ↑ Exo Transition State Optimisation and MO calculatonDOI:10042/to-11491
- ↑ Endo Transition State Optimisation and MO calculatonDOI:10042/to-11489
- ↑ 1,3 Cyclohexadiene Optimisation and MO calculation DOI:10042/to-11485
- ↑ Maleic Anhydride Optimisation and MO calculation DOI:10042/to-11484
- ↑ Exo IRC Calculations DOI:10042/to-11493
- ↑ Endo IRC Calculations DOI:10042/to-11496