Rep:Mod:BTL092
Module 2: Inorganic Computational Chemistry
Analysis of BH3
BH3 Optimisation
Using Gausview, BH3 molecule was drawn with the B-H bonds all set to 1.5Å. The molecule was then optimised employing the DFT/B3LYP method with the basis set fixed to 3-21G.
The Bond length was optimised to 1.19Å and the bond angles to 120o, having a D3H point group. A summary of the optimisation was shown below:
| File Name | bh3_opt |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Energy / Hartree | -26.462 |
| GMS Gradient Norm / Hartree Bohr-1 | 0.000207 |
| Dipole Moment / Debeye | 0 |
| Point Group | D3H |
| Bond Length / Å | 1.19 |
| Bond Angle | 120o |
A gradient smaller than 0.001 indicates that the structure was optimised as energy was converged and a stationary point was found. This could be double checked by looking at the original log file:
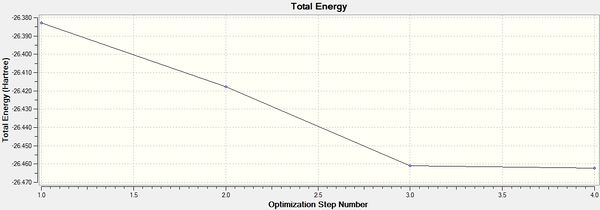
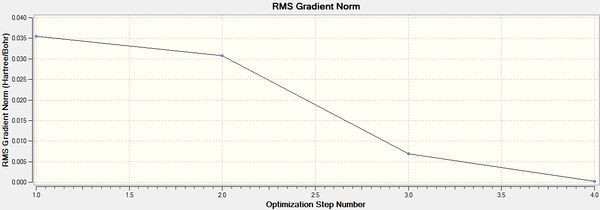
The optimisation of the molecule can be further investigated looking at the optimisation plot. It can be found that the optimisation was done in 4 steps where the fourth step resembles the optimised structure.
The steps of optimisation can also be visualised using Gausview.
| Stage 1 | Stage 2 | Stage 3 | Stage 4 | |
|---|---|---|---|---|

|

|

|

| |
| Energy / Hartree | -26.383 | -26.4177 | -26.461 | -26.4623 |
| RMS Gradient | 0.03552 | 0.03073 | 0.00688 | 0.000207 |
Stage 1 resembles the initial configuration where the B-H bond length was set to 1.5Å. Through each stage of optimisation, the total energy was reduced and the bond length was shortened. The aim of optimisation was to look for the structure of BH3 with a minimal energy. It was also know that the minimum on a curve has a gradient of zero. Therefore, the optimisation was done by convergence to find the energy with the minimal gradient on the potential energy surface. It can be seen from the plot that in stage 4, the change in both energy and gradient was minimal, ie. <0.001, confirming that structure in stage 4, which has a bond length of 1.19Å, energy of -26.462 Hartree and a bond angle of 120o was the optimised structure of the BH3 molecule.
BH3 IR Stretch Calculation and Analysis
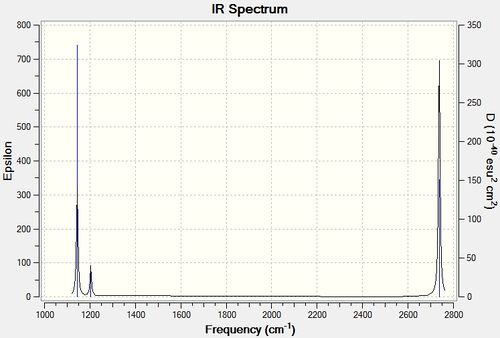
Adopting the optimised structure, the IR spectrum was calculated. It was noted that the frequency calculated has a systematic error of 8%.
The vibrational analysis allow us to confirm that the structure obtained after optimisation was the ground state structure instead of the transition state structure which also has a gradient of zero. The frequency calculation inspects the second derivative of the potential energy surface. Therefore, if all the frequency calculated are positive, it indicates that the structure is at the potential energy minimum, while a positive frequency will indicate a transition state which is has a negative second derivative.
Inspecting the 'low frequencies' in the output file of the frequency calculation allows the better understanding of the vibrations
The 'low frequencies' are the motions of the centre of mass of the molecule. They are much smaller than the frequency of the vibrations. In this case, as a low level method, B3LYP 3-21G, was employed the low frequencies calculated were not as accurate and were out of the +/-10 range.
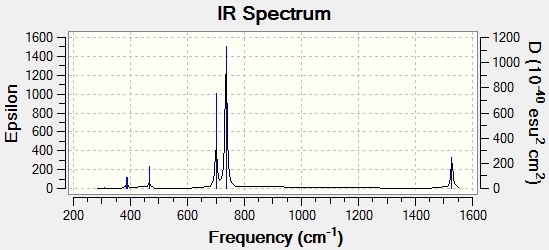
3 Peaks were observed from the spectrum, however, 6 vibration modes were calculated.
The 3 peaks observed are 1144, 1204 and 2737 cm-1, accounting for intensity of 93, 12 and 104. Mode 4 has a point group of A'1, ie. total symmetry. The B-H stretching does not involve a change in dipole moment and therefore was not observed in the spectrum with an intensity of 0. Vibration mode pairs, 2, 3 and 5, 6 belongs to E' point group and are degenerate. Therefore, the pairs appeared as one peak.
BH3 MO and NBO Analysis
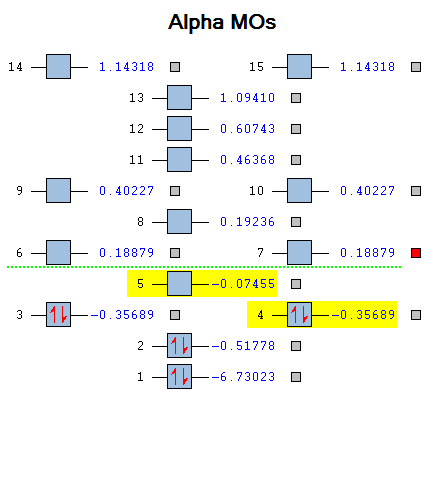
BH3 Molecular Orbitals
With the optimised structure, the molecular orbitals was calculated and was compared to the MO diagram of BH3 predicted using LCAO.
The numbers next to the calculated MOs pictures corresponds to the number on the Alpha MO diagram.
The calculated MOs, in general, agree with the LCAO MOs prediction with similar graphical representation of the electron density However, the relative energy of the 6,7 E' degenerate pairs and the A1' orbital 8 was not consistent. It could be observed that orbital 8 was higher in energy in the calculated MOs but was predicted to be lower in energy than 6 and 7 using LCAO. The energy gap is small and is very hard to determine which is higher in energy. The method used, B3LYP 3-21G, was a low energy method thus lower in accuracy. A higher energy level method like B3LYP 6-311G would provide more information to determine which orbital is higher in energy.
BH3 Natural Bonding Orbitals
The charge distribution was also calculated and was investigated
Red indicates negative atoms while green indicates positive atoms.
It can be seen that Boron was positively charged and Hydrogen atoms were negatively charged having values of 0.332 and -0.110 respectively.
Investigating the log file allows further analysis of the charge distribution and orbitals of the molecule.
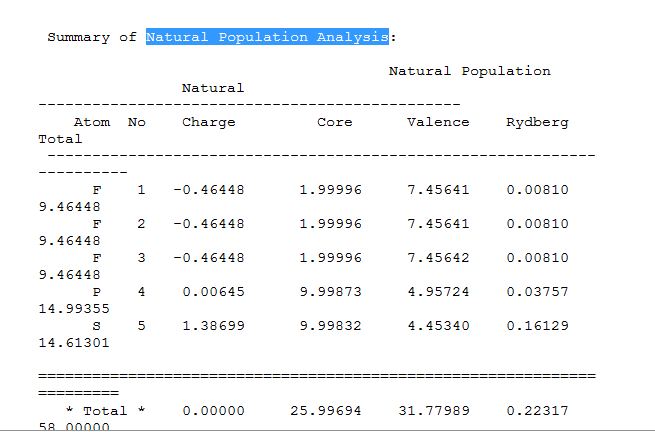
The details of the charge distribution could be found in the Summary of "Natural Population Analysis" section:
It provides a more detailed summary of the charge distribution shown in the figure above.
Bond orbitals can be investigated looking at the "Bond Orbital/ Coefficients / Hybrids" Section:
From the image above it can found that the Boron atom was perfectly sp2 hybridised, consisting 33% s orbital and 66% p orbital. It also showed the low lying non-bonding boron s orbital which consists a lone pair that is 100% on the s orbital.
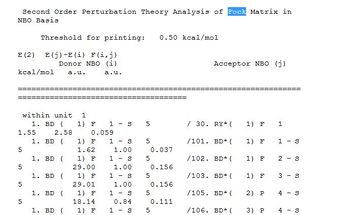
The "Second Order Perturbation Theory Analysis of Fork Matrix in NBO Basis" outlines the mixing between the various MOs and are normally interactions between bonding NBOs into non-bonding or antibonding orbitals:
Only a low energy E2 of 1.51 KJ mol-1 was observed showing that no significant mixing of orbitals could be found in the BH3 molecule.
A summary of the calculated NBOs could also be found in the .log file:
Analysis of TlBr3
The analysis of TlBr3 introduces the use of pseudo-potentials and larger basis set. Both atoms are heavy atoms with Br having 35 electrons and Tl having 81. Standard quantum mechanical methods, would not be able to predict the properties of the structure. Using pseudo-potential, it is possible to replace the complicated effects of the core electrons with an effective potential allowing easier computation using Schrodinger equation.
TlBr3 Optimisation
The symmetry of TlBr3 was first restricted to D3h with a very tight tolerance. The molecule was then optimised using the B3LYP LanL2DZ method which uses a medium level basis set, D95V, on first row atoms and pseudo-potential method on heavier atoms.
The Bond length was optimised to 2.65Å and the bond angles to 120o, having a D3H point group. A summary of the optimisation was shown below:
| File Name | tlbr3_optimisation |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2Dz |
| Charge | 0 |
| Spin | Singlet |
| Energy / Hartree | -91.218 |
| GMS Gradient Norm / Hartree Bohr-1 | 0.0000009 |
| Dipole Moment / Debeye | 0 |
| Point Group | D3H |
| Bond Length / Å | 2.65 |
| Bond Angle | 120o |
TlBr3 Frequency Analysis
The frequency of TlBr3 was calculated to confirm that the structure obtained was the optimised structure.[3]
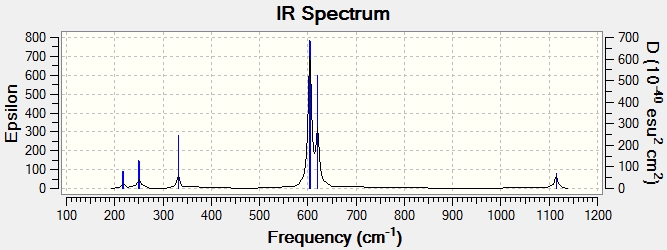
The "low frequencies" were also investigated:
Despite the low frequencies and the low intensity of the vibrations, due to the same symmetry, the IR spectrum of TlBr3 exhibits similar properties as that of BH3. They both have 2 pairs of degenerate stretches and one total symmetric stretch leading to 3 observed peaks despite having 6 different vibrations. Vibration mode 1,2 and 5,6 are degenerate having a frequency of 46 and 211 respectively and 4 being total symmetric with no dipole moment, it was not observed in the spectrum. It can also be observed that the peaks of 1,2 and 3 were overlapped making them hard to distinguish.
The positive values of the frequency of the vibrations confirmed that the structure was at its ground state instead of the transition state, showing that the structure obtained from calculation was the optimised structure for TlBr3.
TlBr3 Discussion
The method of calculation was DFT B3LYP with basis set LANL2DZ.
The energy and confirmation of the resulting structure depends on the method and basis set of calculation. The frequency analysis was used to distinguish the ground state and the transition state by taking into account the second derivative of the potential energy surface, to confirm that the structure obtained from optimisation was at the minima of the potential energy surface. Using the same method for both calculation allows better compairison and the confirmation of the optimised strucutre. Frequency calculated also allow the comparison to literature experimental values for further investigation of the properties and reactivities.
The "low frequencies" fot TlBr3 are -3.4213, -0.0026, -0.0004, 0.0015, 3.9367, 3.9367 and the lowest "real" normal mode is 46.43 cm-1. With a higher level basis set used, the low frequencies were a lot smaller than that in BH3, all within the +/-10cm-1 region.
The literature values for the Tl-Br bond was 2.52Å[4] in TlBr3. The calculated Tl-Br bond was 2.65Å. This shows that the calculated value was of a reasonable value.
The definition of bond in Gausview is more applicable to organic molecules which normally has shorter bond lengths when comparing to inorganic molecules. In the system, when the bond length exceeds a values set by the programme, the bond will disappear. This does not mean that there is no bond, it merely means that the bond is not recognised by the programme and not presented in the graphical representation of the molecule. The interactions between the atoms are still valid and calculated.
A bond is the electromagnetic attraction force of two opposite charge between atoms which holds the atoms within a confined distance despite vibrations. Positive nucleic are attracted to the negative electron density sharing the electron density among the atoms or orbitals over a certain distance, forming a bond.
Analysis of the cis- trans- isomer of Mo(CO)4(PCl3)2
Optimisation
The isomers was first optimised using the B3LYP method with a low level basis set and pseudo-potenital, LANL2MB. A loose convergence criteria was also set by adding 'opt=loose'.
The results from obtained from LANL2MB optimisation:
| cis-isomer | trans-isomer | |
|---|---|---|

|

| |

|

| |
| Energy / Hartree | -617.53 | -617.52 |
| RMS Gradient | 0.0000099 | 0.000113 |
| Dipole Moment / Debeye | 8.46 | 0 |
It can be found that the isomers are very similar in energy. The main difference being the dipole moment, accounted by the position of the PCl3 ligands, where in trans the dipole moment is 0 as the molecule is symmetric.
The low level optimisation gave good bond lengths and angles however the dihedral angles were not well defined. By adjusting the dihedral angles, energy of both isomers can be further minimised, giving the correct group state.
For the cis-isomer, the PCl3 groups were rotated so that the one Cl points up parallel to the axial bond and one Cl of the other PCl3 group points down having a dihedral angle of 0 with the axial bond.
The trans-isomer was modified so that the PCl3 groups eclipse each other with one Cl of each group parallel to one Mo-C bond.

The new conformers were then optimised using a higher level basis set and pseudo-potential, LANL2DZ, under the B3LYP method. The electron convergence was also increase by adding "int=ultrafine scf=conver=9"
| cis-isomer |
trans-isomer |
|
|---|---|---|

|

| |

|

| |
| Energy / Hartree | -623.58 | -623.58 |
| RMS Gradient | 0.0000029 | 0.000037 |
| Dipole Moment / Debeye | 1.31 | 0.30 |
The energy were further minimised, but both isomers are again very similar in energy with the cis-isomer 0.0011 Hartree lower in energy which is equivalent to 2.89 KJ mol-1. At room temperature RT = 2.479 KJ mol-1 which is slightly smaller than the difference between the two isomers. This shows that the isomers might slowly isomerises in room temperature.
However, it was found in the literature[10]that the trans-isomer is in fact the thermodynamic product, lower in energy and will be formed from the cis-isomer in room temperature. This shows that the LANL2DZ basis set and pseudo-potential used in this calculation could be improved. Only the minimal basis, ie. valence s and p orbitals functions, were taken into account for the phosphorus atoms. However, as phosphorus atoms are likely to be hypervalent, the low lying d orbitals should also be taken into account.
Strucutral Analysis
| Mo-P | C=O | P-Cl | Mo-C | |
|---|---|---|---|---|
| cis-isomer | 2.51Å | 1.17Å | 2.24Å | 2.01Å |
| cis-isomer lit. | 2.58Å | N/A | N/A | N/A |
| trans-isomer | 2.44Å | 1.17Å | 2.24Å | 2.06Å |
| trans-isomer lit. | 2.50Å | 1.16Å | N/A | 2.01Å |
The calculated values for both isomers in general coincided with the literature values. The only major deviation were the Mo-P bonds for both isomers which are slightly smaller than the literature values.
| P-Mo-P | P-Mo-C | |
|---|---|---|
| cis-isomer | 94.2 | 89.2, 91.9 |
| cis-isomer lit. | 104.6 | N/A |
| trans-isomer | 177.4 | 91.3, 88.7 |
| trans-isomer lit. | 180 | 87.2 |
Apart from the P-Mo-P in the cis-isomer, the bond angles were consistent and in good agreement with the literature values.
Frequency Analysis
Cis-isomer Frequency
| Vibration Mode | Form of vibration | Frequency / cm-1 | Intensity |
|---|---|---|---|
| 1 |  |
408 | 273.8 |
| 2 |  |
432 | 241.2 |
| 3 |  |
437 | 152.7 |
| 4 |  |
598 | 105.3 |
| 5 |  |
1945 | 763.2 |
| 6 |  |
1948 | 1498.1 |
| 7 |  |
1958 | 632.5 |
| 8 |  |
2023 | 598 |
The low frequencies values are low showing its accuracy. This is due to the higher energy basis set used in this experiement.
No negative frequencies were observed showing that the structure optimised is at ground state.
The calculated CO stretches are 1945, 1948, 1958 and 2023 while the literature values are 1986, 1994, 2001, 2072[14]. The calculated values are smaller than the literature values. However when taking into account the 8% systematic error, the two are in good agreement
trans-isomer Frequency
| Vibration Mode | Form of vibration | Frequency / cm-1 | Intensity |
|---|---|---|---|
| 1 |  |
408 | 727.5 |
| 2 |  |
423 | 168.5 |
| 3 |  |
425 | 166.1 |
| 4 |  |
604 | 138.3 |
| 5 |  |
1950 | 1475.4 |
| 6 |  |
1951 | 1466.9 |
The low values in "low frequencies" are good results due to the high level basis set used.
No negative values were observed indicating that the structure obtained was ground state structure.
The literature value C=O bond stretch for the trans-isomer is 1896[16] while the calculated values were 1950 and 1951. The calculated stretches were very similar in frequencies and thus was observed as one in the spectra. They are also considerably larger than the literature value. This could be due to the systematic error of the calculation.
Mini Project - Analysis on NSF3, NSeF3, PSF3
The following are the proposed structure of the 3 compounds.
The aim of this mini project was investigate the optimised structure of these compounds, their bonding, and the charge distribution.
The three compounds are closely related being derivatives in the same groups. However, how will the charge distribution alter down the periodic table or down the group? How does the bonding changes with these changes? These will be further investigated in this project.
Optimisation
The molecules were all optimised adopting the DFT B3LYP method, first with a lower level basis set 3-21G followed by a higher level 6-311G d,p basis set.
Below are the results obtained after optimising using 6-311G d,p basis set:
| NSF3 |
NSeF3 |
PSF3 |
|
|---|---|---|---|

|

|

| |

|

|

| |
| Energy / Hartree | -752.4 | -2755.7 | -1039.1 |
| RMS Gradient | 0.00005685 | 0.0001649 | 0.00006330 |
| Dipole Moment / Debeye | 1.0500 | 0.0444 | 2.0982 |
It can be observed that the larger the molecule, the more stable it is, with NSeF3 having the lowest energy and NSF3 having the highest energy. The lower in energy of PSF3 than that of NSF3 was expected due to better orbital overlapping of P=S bond than the N=S bond as size of orbitals are of better match. The low energy of NSeF3 might be due to the ability to stabilise the Se-F bond due to larger atomic size and forming possible resonance structure with low lying d orbitals of Se.
PSF3 has the largest dipole moment and NSeF3 being the lowest. This will be further investigated by looking at the charge distributions.
It can also be found that the optimised structure is very different from the structures predicted. This will also be further investigated by looking at the hybridisation of the bonds.
The optimised structures were then confirmed using frequency analysis.
Frequency Analysis
NSF3 IR Stretches
| Vibration Mode | Form of vibration | Frequency / cm-1 | Intensity |
|---|---|---|---|
| 1 |  Symmetric F-S bend Symmetric F-S bend |
466 | 20.2 |
| 2 |  Symmetric F-S stretch Symmetric F-S stretch |
700 | 133.1742 |
| 3 |  Asymmetric F-S stretch Asymmetric F-S stretch |
735 | 207.9035 |
| 4 |  Asymmetric F-S stretch Asymmetric F-S stretch |
735 | 207.8992 |
| 5 |  N=S stretch N=S stretch |
1527 | 93.3837 |
Vibrations with low intensities were also observed at 309 and 387 cm-1. These are bends and stretches which cause minor dipole moment changes therefore not well observed in the spectrum.
The "low frequencies" were also analysed:
Even though a higher level basis set 6-311G d,p was used, the low frequencies were relative high. This shows that the calculations could be further improved using pseudo-potential.
No negative vibrations were observed, indicating that the structure obtained is the optimised structure of NSF3.
NSeF3 IR Stretches
| Vibration Mode | Form of vibration | Frequency / cm-1 | Intensity |
|---|---|---|---|
| 1 |  F-Se bend F-Se bend |
332 | 20.3 |
| 2 |  Asymmetric Se-F stretch Asymmetric Se-F stretch |
604 | 103.6 |
| 3 |  Asymmetric Se-F stretch Asymmetric Se-F stretch |
604 | 103.4 |
| 4 |  Symmetric Se-F stretch Symmetric Se-F stretch |
620 | 81.6 |
| 5 |  N-Se stretch N-Se stretch |
1114 | 19.5 |
Vibrations with low intensities were also observed at 216 and 250 cm-1. These are bends and stretches which cause minor dipole moment changes therefore not well observed in the spectrum.
The shape of the spectrum of NSeF3 is very similar to that of NSF3 apart from the swapping in relative frequencies of the degenerate asymmetric stretching pair and the symmetric stretching mode (2 in NSF3 and 4 in NSeF3). The frequencies and intensity are all lower than that in NSF3, indicating lower bond order which coincides with the optimised structure.
The "low frequencies" were also analysed:
Even though a higher level basis set 6-311G d,p was used, the low frequencies were relative high especially in the positive region. This shows that the calculations could be further improved using pseudo-potential.
No negative vibrations were observed, indicating that the structure obtained is the optimised structure of NSeF3.
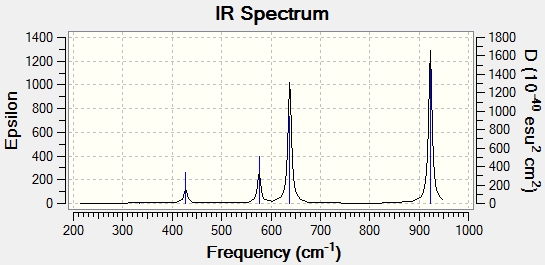
PSF3 IR Stretches
| Vibration Mode | Form of vibration | Frequency / cm-1 | Intensity |
|---|---|---|---|
| 1 |  Symmetric F-S bend Symmetric F-S bend |
427 | 35.8 |
| 2 |  Symmetric F-S stretch Symmetric F-S stretch |
575 | 74.3 |
| 3 |  Asymmetric F-S stretch Asymmetric F-S stretch |
638 | 150.4 |
| 4 |  Asymmetric F-S stretch Asymmetric F-S stretch |
638 | 150.6 |
| 5 |  P=S stretch P=S stretch |
922 | 374.2 |
Vibrations with low intensities were also observed at 238 and 334 cm-1. These are bends and stretches which cause minor dipole moment changes therefore not well observed in the spectrum.
Again the shape of spectrum is similar to that of NSF3 but the frequencies are also lower than NSF3 but higher than NSeF3. The effect is more significant when looking at the N=S stretch, N-Se stretch and the P=S stretch. This indicates that the bond order of PSF3 is lower than NSF3 but higher than NSeF3.
The "low frequencies" were also analysed:
Even though a higher level basis set 6-311G d,p was used, the low frequencies were relative high. This shows that the calculations could be further improved using pseudo-potential.
No negative vibrations were observed, indicating that the structure obtained is the optimised structure of PSF3.
Structural Analysis
NSF3 – Bond length: N=S: 1.43, S-F: 1.61
- Bond angle: N-S-F: 123.1o
NSeF3 – Bond length: N=Se: 1.59, Se-F: 1.77
- Bond angle: N-Se-F: 124.5o
PSF3 – Bond length: P=S: 1.83, S-F: 1.64
- Bond angle: P-S-F: 124.7o
The S-F / Se-F bond length increases with increasing atomic size. The N=S / N-Se / P=S bond length increases with increasing atomic size but significantly when substituting N with P which is down the same group. This might be due to the decrease in electronegativity to withdraw electrons from negatively charged S atom. To better understand this periodicity, derivatives of more elements should be investigated.
NBO Analysis
Bright red indicate a high negative charge while a bright green indicates a high positive charge.
NSF3 NBO
From the graphic representation and the summary of "Natural Population Analysis", the charge distribution among the molecule can be found. The N atom and the F atoms are negatively charged with a value of -0.401 and -0.269 respectively while the S atom is highly positively charged with a value of 1.206.
The hybridisation of the molecule is not as well defined as simple molecules like BH3. From the Bond Orbital / Coefficients / Hybrids section, it can be found that the N=S bond is 53.17% contributed by the N orbitals, which have a hybridsation of 20.58%s + 78.8%p and 0.62%d, and 46.83% by the S orbitals which is 46.55%s + 52.85%p and 0.60%d. These contributed to the double bond seen in the optimised structure.
The S-F bonds is 19.54% contributed by the S orbitals which are 17.79%s + 46.12%p and 36.08% and 80.46% contributed by the F orbitals which are 13.20%s + 86.7%p and 0.1%d contributing to the majorly single bonded S-F bond.
1 lone pair is also found on the N atom in an orbital which is 79.45%s + 20.53%p
E2 is found to be 0.58 which is relatively small indicating that there is no significant mixing of orbitals in NSF3[26]
NSeF3 NBO
From the graphic representation and the summary of "Natural Population Analysis", the charge distribution among the molecule can be found. The N atom and the F atoms are negatively charged with a value of -0.354 and -0.288 respectively while the S atom is highly positively charged with a value of 1.218. With Se instead of S the positive charge builds up around the central atom. The negative charge value for F atoms also increase while the negativity of N atom dropped.
It can be found that the N-Se bond is 49.91% contributed by the N orbitals, which have a hybridsation of 9.77%s + 90.01%p and 0.21%d, and 50.09% by the S orbitals which is 47.51%s + 52.34%p and 0.15%d. These contributed to the single bond seen in the optimised structure.
The Se-F bonds is 16.71% contributed by the S orbitals which are 17.50%s + 47.03%p + 35.46% and 83.29% contributed by the F orbitals which are 9.32%s + 90.61%p contributing to the majorly single bonded S-F bond.
1 lone pair is also found on the N atom in an orbital which is 90.28%s + 9.72%p
E2 is found to be 11.54. This shows that mixing does occur in this molecule but due to the relative small magnitude it is not significant. Value larger than 20 will indicate significant mixing of orbitals.[27]
PSF3 NBO
From the graphic representation and the summary of "Natural Population Analysis", the charge distribution among the molecule can be found. The F atoms remain negative with a value of -0.28, however with P replacing N, it is now relatively neutral atoms having a value of 0.014. S remains negatively charged but the negativity has reduced to 0.824. The lacking of electromagnetic attraction of P and S explains the significantly longer bond length when comparing to the other two compounds.
It can be found that the P-S bond is 29.20% contributed by the N orbitals, which have a hybridsation of 11.91%s + 87.32%p and 0.77%d, and 70.80% by the S orbitals which is 47.86%s + 51.45%p and 0.68%d. These contributed to the double bond seen in the optimised structure.
The S-F bonds is 19.08% contributed by the S orbitals which are 17.36%s + 48.32%p + 34.32% and 80.92% contributed by the F orbitals which are 12.70%s + 87.21%p contributing to the majorly single bonded S-F bond.
4 lone pair is also found on the N atom in an orbital which is 89.61%s + 10.38%p
E2 is found to be 1.55 which is a relatively small value therefore it can be assumed that there is no mixing of orbitals in this molecule.[28]
In all 3 of the compounds the central atom-F bond are all hybridised in similar ways giving a single bond representation. The charge distribution of NSF3 and NSeF3 are similar with slightly different magnitudes due to the replacing of S with Se. However with the replacing of S with P the charge distribution changed dramatically and so and the hybridisation of the bonds. In the P=S bond, contribution of central atom is dominant while in the other two compounds, the atoms have a more even contribution.
With complex hybridisation system as calculated here, the VSEPR representation becomes less valid. However, more accurate calculation, such as taking into account the lower lying d orbitals or taking into account any delocalised electron will provide better understand of these three compounds.
For more details on the NBO analysis please refer to the references where the original log files could be found.
Molecular Orbital Analysis
Using the optimised structures, Molecular Orbitals can be calculated. In this experiment we will focus on the MO of NSF3.
As seen in the MO diagram, there are 25 occupied orbitals. Only valence molecular orbitals HOMO-2, HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2 will be discussed.
The Molecular orbitals involve overlapping of multiple p orbitals making it difficult to predict using LCAO especially when reaching the LUMO region.
It is found that in this molecule even the LUMO+1 is slightly bonding, which illustrates the stability of the compounds.
Apart from these MOs there are also some interesting occupied orbitals that were calculated. Please note that the number corresponds to the number of the calculated MO diagram.
These orbitals were formed by overlapping of p orbitals. This give rise to the possibility for delocalisation of electrons in these orbitals. Especially in orbital 17 it can be seen than electrons are delocalised among the S-F bonds. This coincides with the NBO analysis which described that the S-F bonds have a significant p orbital characteristics.
Conclusion
The three molecules NSF3, NSeF3 and PSF3 were successfully optimised. The optimisations were confirmed by frequency analysis. The optimised structures was also further investigated by looking into the structural properties and the charge distribution to allow the better understanding of the bonding on the compounds and the effects of periodicity.
The calculations could be further improved using pseudo-potential, taking into account the d orbital contributions. The hybridisations in these molecules are complex and further investigation is required to acquire a better understanding of the bonding of these compounds.
Due to multiple p orbital contribution, the molecular orbitals of NSF3 are complex and LCAO is insufficient to describe the effects. Further calculations of the orbitals of the other two compounds will provide better understanding on how the properties and reactivity changes by substituting the atoms.
References
- ↑ http://www.huntresearchgroup.org.uk/teaching/teaching_MOs_year2/L4_Tut_MO_diagram_BH3.pdf
- ↑ BH3 MO and NBO Calculation DOI:10042/to-10591
- ↑ TlBr3 Frequency Calculation DOI:10042/to-10641
- ↑ J. Blixt, J. Glaser, J. Mink, I. Persson, P. Persson, M. Sandstroem, J. Am. Chem. Soc., 1995, 117 (18), pp 5089–5104 DOI:10.1021/ja00123a011
- ↑ Cis-isomer LANL2MB Optimisation DOI:10042/to-10526
- ↑ Trans-isomer LANL2MB Optimisation DOI:10042/to-10527
- ↑ http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year3/10b_MoC4L2_opt.html
- ↑ Cis-isomer LANL2DZ Optimisation after Dihedral Angle adjustment DOI:10042/to-10532
- ↑ Trans-isomer LANL2DZ Optimisation after Dihedral Angle adjustment DOI:10042/to-10533
- ↑ D. J. Darensbourg, Inorg. Chem., 1979, 18(1), pp 14-17 DOI:10.1021/ic50191a003
- ↑ G. Horgath, T. Norman, Inorganica Chemic Acta, 1997, 254, 167-171 DOI:10.1016/S0020-1693(96)05133-X
- ↑ G. Horgath, T. Norman, Inorganica Chemic Acta, 1997, 254, 167-171 DOI:10.1016/S0020-1693(96)05133-X
- ↑ Cis-isomer Frequency Calculation DOI:10042/to-10592
- ↑ E. C. Alyea, S. Song, Inorg. Chem., 1995, 34 (15), pp 3864-3873 DOI:10.1021/ic00119a006
- ↑ trans-isomer Frequency Calculation DOI:10042/to-10593
- ↑ F. A. Cotton, D. J. Darensbourg, S. Klein, B. W. S. Kolthammer, Inorg. Chem., 1982, 21(7), pp 2661-2666 DOI:10.1021/ic00137a026
- ↑ NSF3 3-21 Optimisation DOI:10042/to-10642
- ↑ NSeF3 3-21 Optimisation DOI:10042/to-10643
- ↑ PSF3 3-21 Optimisation DOI:10042/to-10644
- ↑ NSF3 6-311 Optimisation DOI:10042/to-10658
- ↑ NSeF3 6-311 Optimisation DOI:10042/to-10659
- ↑ PSF3 6-311 Optimisation DOI:10042/to-10660
- ↑ NSF3 Frequency Calculation DOI:10042/to-10832
- ↑ NSeF3 Frequency Calculation DOI:10042/to-10882
- ↑ PSF3 Frequency Calculation DOI:10042/to-10885
- ↑ NSF3 NBO Calculation DOI:10042/to-10886
- ↑ NSeF3 NBO Calculation DOI:10042/to-10887
- ↑ PSF3 NBO Calculation DOI:10042/to-10888