Rep:Mod:BTL091
Module 1: Molecular Mechanics and Semi-empirical Molecular Orbital Methods for structural and spectroscopic evaluations
Modelling using Molecular Mechanics
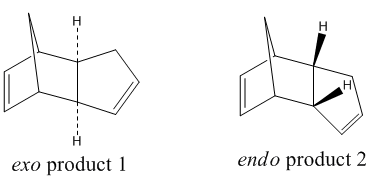
Hydrogenation of Cyclopentadiene Dimer
Dimerisation of Cyclopentadiene
Cyclopentadiene dimerises via the Diels-Alder Reaction producing specifically the endo dimer(2) instead of the exo dimer (1)[1]
Using the molecular mechanics calculation (MM2), the energy of the two isomers was investigated.
| ' | Exo dimer 1 |
Endo dimer 2 |
| Stretch / kcal mol-1 | 1.286 | 1.251 |
| Bend / kcal mol-1 | 20.579 | 20.848 |
| Stretch-Bend / kcal mol-1 | -0.838 | -0.836 |
| Torsion / kcal mol-1 | 7.657 | 9.511 |
| Non-1,4 VDW / kcal mol-1 | -1.417 | -1.543 |
| 1,4 VDW / kcal mol-1 | 4.232 | 4.320 |
| Dipole-Dipole / kcal mol-1 | 0.378 | 0.448 |
| Total Energy / kcal mol-1 | 31.877 | 33.998 |
| Energy Difference / kcal mol-1 | 2.121 |
As shown in the table above, the endo product is 2.121 kcal mol-1 higher in energy than the exo product. This difference is dominated by the torsion energy due to the backward bending of the cyclopentadiene ring in the endo dimer causing the sets of carbons to eclipse with each other. This shows that the dominant product of the dimerisation of cyclopentadiene, the endo dimer, does not occur under a thermodynamic pathway as the endo product is relatively unstable when comparing to the exo product. Literature experiments have shown that the activation energy for the formation of the endo product is 32.97 kcal mol-1 and is lower than that of the exo product which is 37.41 kcal mol-1. The reaction is endo selective due to the kinetic pathway where transition state is stablisied by the p-orbital interactions between the two cyclopentadienes.[2]
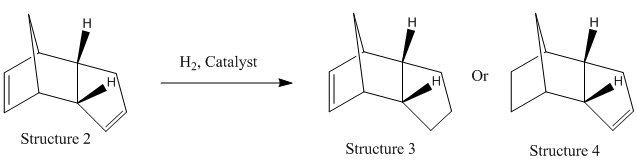
Hydrogenation of Cyclopentadiene Dimer
The hydrogenation of the endo product 2 gives 2 isomers, structure 3 and 4. Using the MM2 approach, the energies of the two isomers were analysed.
| ' | Structure 3 |
Structure 4 |
| Stretch / kcal mol-1 | 1.249 | 1.097 |
| Bend / kcal mol-1 | 19.157 | 14.524 |
| Stretch-Bend / kcal mol-1 | -0.835 | -0.549 |
| Torsion / kcal mol-1 | 11.076 | 12.498 |
| Non-1,4 VDW / kcal mol-1 | -1.641 | -1.070 |
| 1,4 VDW / kcal mol-1 | 5.797 | 4.512 |
| Dipole-Dipole / kcal mol-1 | 0.162 | 0.141 |
| Total Energy / kcal mol-1 | 34.964 | 31.152 |
| Energy Difference / kcal mol-1 | 3.812 |
Structure 4 is 3.812 kcal mol-1 lower in energy than that of structure 3 due to a significant lower bending energy. Calculated using ChemBio3D, the sp2 bond angle in structure 3 and structure 4 are 108o and 113o respectively. The large difference between the bond angle in structure 3 and the ideal sp2 bond angle of 120o give rise to the high bending energy. Structure 4 is therefore thermodynamically more stable and favourbale and is the major product of the hydrogenation of dimer 2.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
A key intermediate in the total synthesis of Taxol exhibits atropisomerism where one isomer transforms into another via a rotation about a single bond. The two isomers, structure 9 and 10, are shown below. Structure 9 and 10 atropisomerises via the rotation of the carbonyl group and are different in energies.
Using both MM2 method and the MMFF94 method, the energy of the two atropisomers, structure 9 and 10 were analysed. During the analysis, the cyclohexane ring was kept in a chair conformation to minimize the energy. There are more than one structure for the carbonyl down isomer 10. Apart from the lowest energy structure another structure with higher energy is illustrated below.
| Intermediate | MM2 | MMFF94 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Stretch / kcal mol-1 | Bend / kcal mol-1 | Stretch-Bend / kcal mol-1 | Torsion / kcal mol-1 | Non-1,4 Van de Waal's / kcal mol-1 | 1,4 Van de Waal's / kcal mol-1 | Dipole/Dipole / kcal mol-1 | Total Energy / kcal mol-1 | Total Energy / kcal mol-1 | |
| Atropisomer 9 carbonyl upwards |
2.784 | 16.5406 | 0.430 | 18.254 | -1.553 | 13.109 | -1.725 | 47.840 | 70.575 |
| Atropisomer 10 carbonyl downwards a |
2.621 | 11.339 | 0.343 | 19.678 | -2.167 | 12.872 | -2.003 | 42.683 | 60.561 |
| Atropisomer 10 carbonyl downwards b |
3.029 | 16.399 | 0.335 | 20.419 | -1.064 | 13.877 | -1.824 | 51.171 | 73.343 |
Using the MM2 method, it can be observed that structure a of atropisomer 10, which has the carbonyl group downwards, is the thermodynamically more stable structure, having a total energy of 42.683 kcal mol-1, with a significantly lower bending energy. The MMFF94 method also coincides with the MM2 method, with structure a, underlined above, being the more stable structure with a lower energy.
Hyperstable alkenes are ring alkenes that are more stable than its corresponding alkanes due to a lower steric strain. Both atropisomer 9 and 10 are examples of hyperstable akenes thus, very stable and undergo slow reaction.[3]
Modelling Using Semi-empirical Molecular Orbital Theory
Regioselective Addition of Dichlorocarbene
Molecular Orbitals Modelling
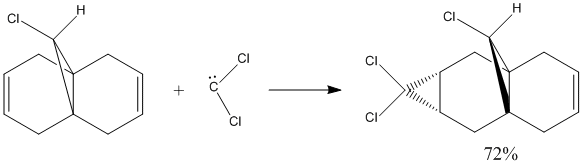
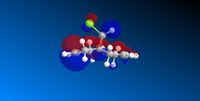
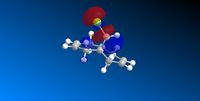
The reaction of compound 12 with electrophiles like dichlorocarbene and peracids were found to be under orbital control. Therefore, by predicting the energy of the molecule and the energy alongside with the location of the orbitals, the regioselectivity can be predicted.
After optimising using MM2, the molecular orbitals were predicted using MOPAC/PM6.
| ' | Compound 12 |
| Stretch / kcal mol-1 | 0.62 |
| Bend / kcal mol-1 | 4.74 |
| Stretch-Bend / kcal mol-1 | 0.040 |
| Torsion / kcal mol-1 | 7.66 |
| Non-1,4 VDW / kcal mol-1 | -1.07 |
| 1,4 VDW / kcal mol-1 | 5.79 |
| Dipole-Dipole / kcal mol-1 | 0.11 |
| Total Energy / kcal mol-1 | 17.89 |
| HOMO -1 | HOMO | LUMO | LUMO +1 | LUMO +2 |
|---|---|---|---|---|
 |
 |
 |
 |
 |
The predicted MOs, especially the HOMO, HOMO -1 and LUMO are supported by the experimental data of the reaction of compound 12 with dichlorocarbene which forms a mixture of product. The product where the addition occurs on syn to the chloride is the major product with a literature abundance of 72%.[4][5]
The HOMO shows a high proportion of electron density is located at the pi-orbital of the C=C double bond syn to, ie. on the same side as, the C-Cl bond. The LUMO, on the other hand, shows high electron density at the pi* antibonding orbital of the C=C bond anti to the C-Cl bond. The low energy HOMO -1 also shows a high electron density at the C=C double bond anti to the C-Cl bond. These orbitals coincided by showing that the the anti C=C bond is not favourable for the dichlorocarbene addition, due to orbital and energy mismatch, but the C=C syn to the C-Cl bond is susceptible to electrophilic attack, having high electron density orbitals with the right energy and symmetry, to give the major product, shown in the above scheme.
Spectroscopic Modelling
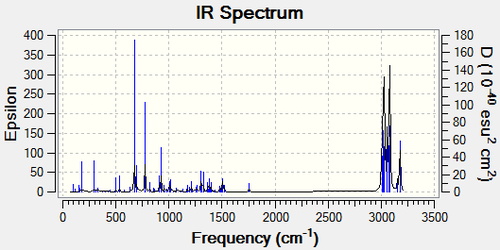
After optimising the molecule using MOPAC/PM6 and SCAN, the IR spectrum of molecule 12 and its mono-hydrogenated derivative can be predicted. Compound 12 exhibits a Cs symmetry, but after the hydrogenation, the plane of reflection was removed due the the change of the ring structure and the distribution of orbitals
| Compound 12 | Mono-hydrogenated Derivative |
|---|---|

|
|
| ' | C=C Stretches | C-Cl Stretches | C-H Bending |
| Compound 12 | 1736.39cm-1, 1757.08cm-1 | 689.53cm-1 | 769.66cm-1 |
| Mono-hydrogenated Derivative | 1758.07cm-1 | 673.90cm-1 | 774.98cm-1 |
2 C=C stretches were observed for compound 12 due to the different C=C in the molecule, with one syn and the other anti to the C-Cl bond. The C-Cl bond coincided with the expectation with a strong absorption within the 600-800cm-1 region. The C=C stretches were a bit larger than expected but when taking into account that the prediction has an error of approximately 8%, they fit the 1620-1680cm-1 expectation. It can also be observed that the C-Cl stretch is larger after the hydrogenation. This is due to the unavailability for the C-Cl σ* bond to overlap with the pi-bond of the C=C bond anti to the C-Cl bond.
Monosaccharide Chemistry: Glycosidation
The neighbouring group effect in glycosidation showed above, was analysed using computational methods. In this experiment, methyl group was used as the R groups. This is because of the fact that it is the smallest alkyl group, leading to a small electron count, and it inability to form hydrogen bonds when comparing to R=H. These factors made methyl group a good choice for modeling the monosaccharide derivatives, as it reduces the error and work load required.
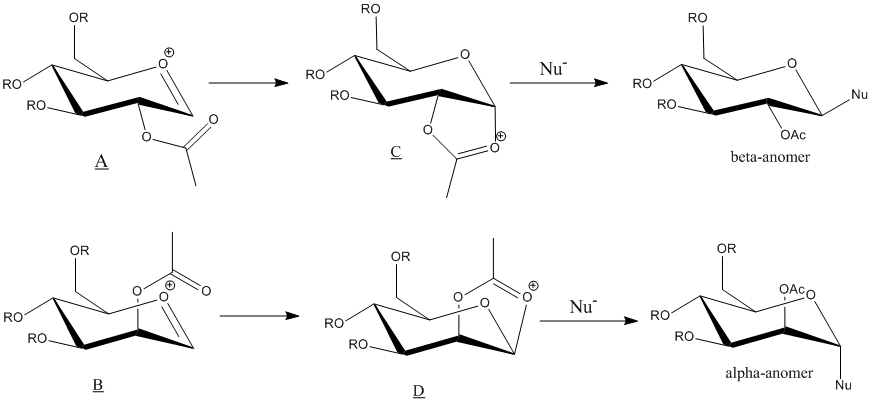
The energy oxonium cations, A and B, involved in the glycosidation was calculated using MM2 method and MOPAC/PM6 method. However, the semi-empirical molecular orbital method, MOPAC/PM6, is more preferred in this case. MM2 method, as a purely classical mechanical treatment of a molecule, has limitation. It is not able to take into account the interactions between the oxygen lone pair on the acetyl group and the p* orbital on the oxonium cation ring. These interactions are crucial in neighbouring-group-participation which causes the regioselectivity of the reactions. Therefore, the MOPAC/PM6 method, which accounts for the quantum mechanics of the molecule, is more suitable in the analysis of these monosaccharide derivatives
A' and B' are conformers of A and B respectively where the direction of the acetyl group was adjusted. All jmol objects shown below are optimised using the MOPAC/PM6 method.
| Strucutre | MM2 | PM6 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Stretch / kcal mol-1 | Bend / kcal mol-1 | Stretch-Bend / kcal mol-1 | Torsion / kcal mol-1 | Non-1,4 Van de Waal's / kcal mol-1 | 1,4 Van de Waal's / kcal mol-1 | Charge-Dipole / kcal mol-1 | Dipole-Dipole / kcal mol-1 | Total Energy / kcal mol-1 | Heat of Formation / kcal mol-1 | |
| A |
2.57 | 11.05 | 1.01 | 1.93 | 1.10 | 18.64 | -22.94 | 6.52 | 19.88 | -91.65 |
| A' |
2.38 | 9.51 | 0.89 | 2.26 | -2.86 | 19.24 | -0.92 | 3.74 | 34.23 | -76.30 |
| B |
2.79 | 10.84 | 0.96 | 0.50 | -1.64 | 18.53 | -21.23 | 6.02 | 19.31 | -88.73 |
| B' |
2.56 | 10.23 | 0.90 | 0.23 | -1.27 | 18.67 | -9.04 | 4.77 | 27.04 | -77.51 |
Both methods coincided by pointing out that both A and B are more stable than A' and B'. The lower in energy leads and the fact that A and B has a more favourable orientation for the acetyl group to nucleophilically attack the oxonium cation ring causes the reaction to regioselectively form C and D respectively.
Structure C and D and its conformers were also analysed using MM2 and MOPAC/PM6.
| Strucutre | MM2 | PM6 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Stretch / kcal mol-1 | Bend / kcal mol-1 | Stretch-Bend / kcal mol-1 | Torsion / kcal mol-1 | Non-1,4 Van de Waal's / kcal mol-1 | 1,4 Van de Waal's / kcal mol-1 | Charge-Dipole / kcal mol-1 | Dipole-Dipole / kcal mol-1 | Total Energy / kcal mol-1 | Heat of Formation / kcal mol-1 | |
| C |
2.01 | 13.69 | 0.70 | 7.52 | -2.51 | 17.74 | -10.61 | -1.06 | 27.50 | -91.66 |
| C' |
2.57 | 18.72 | 0.70 | 4.71 | -3.53 | 18.69 | -0.15 | -1.41 | 40.03 | -67.91 |
| D |
1.71 | 18.54 | 0.79 | 6.02 | -2.32 | 16.61 | -14.42 | 1.10 | 28.03 | -89.94 |
| D' |
2.58 | 20.20 | 0.74 | 5.99 | -2.79 | 18.70 | -3.91 | -0.61 | 40.90 | -65.74 |
Both methods coincided by pointing out that C and D are lower in the energy thus more stable than C' and D'. It can be observed that the heat of formation of C is approximately the same as A and this that for D is same as B. The differences in energy between C and C' and D and D' are 23.75 and 24.2kcal mol-1 respectively.
The stability of C and D also leads to the diastereospecificity of the glycosidation reaction. Due to the large differences in energy, from Boltzmann Distribution, it can be found that C and D will be approximately 100% abundant. C and D both only allow nucleophiles to attack from one specific side, regioselectively producing the beta-anomer from C and alpha-anomer from D.
The 2 methods, MM2 and MOPAC/PM6 give different results. As seen in the above tables, MM2 method gives energy as total steric energy while MOPAC/PM6 gives a energy of formation which is a negative value and is large in magnitude. Bond angles and bond length also differ. Taking structure A as example, the MOPAC/PM6 optimises A to give a structure with a bond angle of 114o between the two oxygen atom in the acetyl group and a bond length of 0.16nm between the carbonyl oxygen and the hexose ring while the results using MM2 are 124o and 0.25nm respectively.[8]
Structure based Mini project using DFT-based Molecular orbital methods
Investigating the Regioselectivity of the Baeyer-Villiger reaction
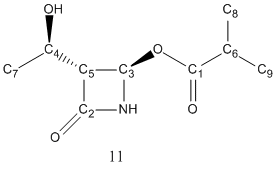
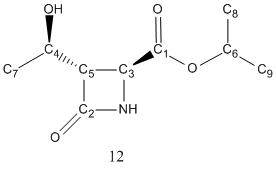
The above scheme has shown how the Baeyer-Villiger reaction can produce a mixture of products. It coverts ketones into esters by reacting it with peracids such as mCPBA. However, for unsymmetric ketones such as strucutre 10 shown in the the above scheme, it can insert the oxygen atom either between the carbonyl group or the alpha-carbon, producing two possible regioisomeric products, structure 11 and 12.
Regioselectivity with different R groups
Regioselectivity arises when different R group was used. The transition state of the reaction is positively charged, and the regioselectivity depends on how able the migrating substituent is to stabilise it.
| R group | Abundance of 11 | Abundance of 12 |
| Ph | 100% | 0% |
| t-Bu | 0% | 100% |
| i-Pr | 52% | 100% |
| c-Pr | 100% | 0% |
It can be found that with R=i-Pr the reaction has minimal regioselectivity. This is because as a secondary alkyl group, it is not able to stabilise the transition state. In this experiment, R=i-Pr, was analysed to differentiate the two products using computational methods.
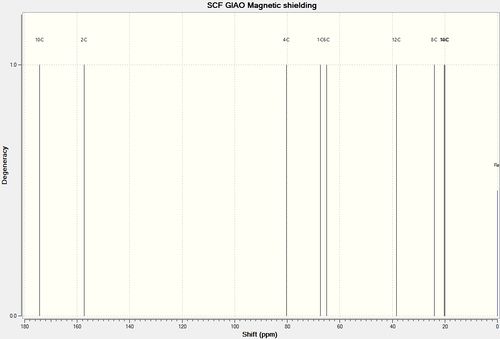
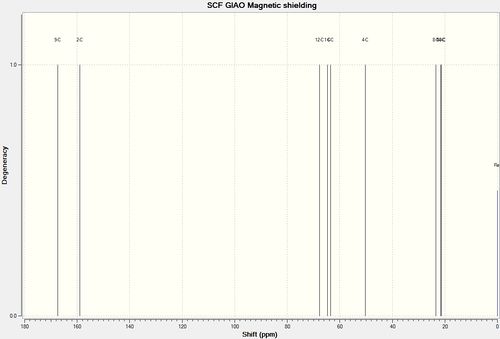
Analysis with 13C NMR
Using the GIAO approach, the 13C NMR was calculated.
| Strucutre 11 with R=i-Pr | Strucutre 12 with R=i-Pr |
|---|---|
|
|
It was noted that there is a systematic error present in that carbonyl shift. They are corrected by δcorr=0.96δcalc + 12.2
| Carbon Atom | δcalc/ppm | δcorr/ppm | δlit/ppm | δcorr-expt/ppm | % differences |
|---|---|---|---|---|---|
| Carbon 1 | 174.2 | 179.4 | 177.6 | 1.8 | 1.0 |
| Carbon 2 | 157.4 | 163.3 | 167.2 | -3.9 | 2.3 |
| Carbon 3 | 80.3 | 80.3 | 75.9 | 4.4 | 5.8 |
| Carbon 4 | 67.5 | 67.5 | 65.2 | 2.3 | 3.5 |
| Carbon 5 | 65.0 | 65.0 | 63.9 | 1.1 | 1.7 |
| Carbon 6 | 38.5 | 38.5 | 34.0 | 4.5 | 13.2 |
| Carbon 7 | 24.0 | 24.0 | 21.3 | 2.7 | 12.7 |
| Carbon 8 | 20.3 | 20.3 | 18.9 | 1.4 | 7.4 |
| Carbon 9 | 19.9 | 19.9 | 18.8 | 1.1 | 5.8 |
| Carbon Atom | δcalc/ppm | δcorr/ppm | δlit/ppm | δcorr-expt/ppm | % differences |
|---|---|---|---|---|---|
| Carbon 1 | 167.4 | 172.9 | 170.8 | 2.1 | 1.2 |
| Carbon 2 | 159.0 | 164.8 | 168.3 | -3.5 | 2.1 |
| Carbon 3 | 67.7 | 67.7 | 69.7 | -2.0 | 2.9 |
| Carbon 4 | 64.7 | 64.7 | 64.5 | 0.2 | 0.3 |
| Carbon 5 | 63.5 | 63.5 | 64.0 | -0.5 | 0.8 |
| Carbon 6 | 50.2 | 50.2 | 50.0 | 0.2 | 0.4 |
| Carbon 7 | 23.4 | 23.4 | 21.9 | 1.5 | 6.8 |
| Carbon 8 | 21.6 | 21.6 | 21.8 | -0.2 | 0.9 |
| Carbon 9 | 21.4 | 21.4 | 21.3 | 0.1 | 0.5 |
In both cases, all deviations are less than 5ppm, therefore were in acceptable ranges. It can be found that in both cases, C2 has large deviation this is due to its bonding to two heavy atoms, N and O which alters the calculation even after correction. For structure 11 it can also be seen that there is a large deviation for C6. This might be due to the incorrect optimisation of the molecule especially around the isopropyl group.
From the spectra, it can be observed that the largest differences in chemical shift between the two structure occurs at C1 and C3. In both cases, the shift for structure 11 is much larger, therefore from inspecting these two carbonyl carbons, the regioisomers can be differentiated.
Analysis with 15N NMR
The regioisomers can also be differentiated using 15N NMR.
| Strucutre 11 with R=i-Pr | Strucutre 12 with R=i-Pr |
|---|---|

|

|
| Strucutre | 15N NMR Chemical Shift / ppm |
| 11 | 131.8 |
| 12 | 125.9 |
Due to the large difference in the 15N NMR Chemical Shift, the 15N NMR can also help differentiate between the two regioisomers, 11 and 12.
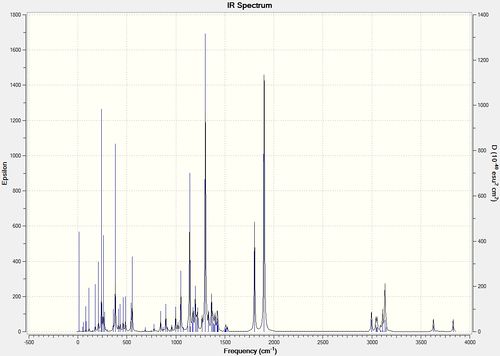
Analysis with Infra-red Spectroscopy
The IR spectrum of Structure 11 and 12 with R=i-Pr was predicted and compared to the literature values.
| Strucutre 11 with R=i-Pr | Strucutre 12 with R=i-Pr |
|---|---|

|
|
| ' | Calc. Acetidinone ring C=O Stretch | Lit. Acetidinone ring C=O Stretch | Calc. Ester C=O Stretch | Lit. Ester C=O Stretch |
| Structure 11 R=i-Pr | 1887cm-1 | 1783cm-1 | 1817cm-1 | 1740cm-1 |
| Structure 12 R=i-Pr | 1900cm-1 | 1749cm-1 | 1802cm-1 | 1721cm-1 |
It can be noted that the IR calculation has a systematic error of approximately 8% leading to the difference between calculated values and the literature values. IR spectrum can help assist the differentiation of the two regioisomer, especially when the difference in stretches are more significant. In this case it is not as clear due to the systematic error. The lower ester C=O stretch in structure 12 can still be observed and it coincides with the literature. However, in this case, the NMR method is more conclusive.[13]
References
- ↑ W. C. Herndon, C. R. Grayson, J. M. Manion, J. Org. Chem., 32 (3), 1967, 526-529 DOI:10.1021/jo01278a003
- ↑ Clayden, Greeves, Warren, Organic Chemistry, 2001, p916-917
- ↑ Wilhelm F. Maier, Paul Von Rague Schleyer, J. Am. Chem. Soc., 1981, 103, 1891. DOI: 10.1021/ja00398a003
- ↑ B. Halton, R. Boese, H. S. Rzepa, J. Chem. Soc., Perkin Trans. 2, 1992, 447
- ↑ B. Halton, S. G. G. Russell, J. Org. Chem., 1991, 56, 5556 DOI:10.1021/jo00019a015
- ↑ http://hdl.handle.net/10042/to-10433
- ↑ http://hdl.handle.net/10042/to-10434
- ↑ D. M. Whitfield, T. Nukada, Carbohydr. Res., 2007, 342, 1291. DOI:10.1016/j.carres.2007.03.030
- ↑ http://hdl.handle.net/10042/to-10380
- ↑ http://hdl.handle.net/10042/to-10381
- ↑ http://hdl.handle.net/10042/to-10431
- ↑ http://hdl.handle.net/10042/to-10432
- ↑ M. Laurent, M, Cérésiat,J. Marchand-Brynaert, J. Org. Chem., 2004, 69(9)pp 3194–319 DOI: 10.1021/jo030377y