Rep:Mod:BOOK123
Introduction to Molecular Modelling 2 - Report
Ammonia
Molecule Name: NH3
Calculation Method: B3LYP
Basis Set: 6-31G(d,p)
Final Energy (au): -56.55777
RMS Gradient (au): 0.00000485
Point Group: C3v
Optimised N-H Bond Distance: 1.018 A
Optimised H-N-H Bond Angle: 105.741°
Item Table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986267D-10
Optimization completed.
-- Stationary point found.
Jmol Image of Ammoniɑ
Ammonia |
The optimised NH3 molecule is linked here.
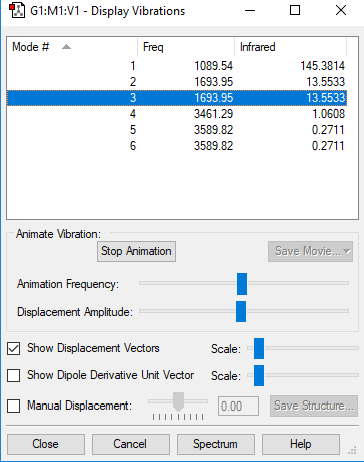
| Mode | Frequency (cm-1) | Intensity |
|---|---|---|
| 1 | 1090 | 145 |
| 2 | 1694 | 14 |
| 3 | 1694 | 14 |
| 4 | 3461 | 1 |
| 5 | 3590 | 0 |
| 6 | 3590 | 0 |
Screenshot of the vibrational modes of ammonia:
How many modes do you expect from the 3N-6 rule?
3(4)-6 = 6 expected vibrational modes.
Which modes are degenerate (ie have the same energy)?
Modes 2 and 3 and modes 5 and 6 are degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Bond stretching modes are 4,5 and 6. Bond bending modes are 1 and 3. Mode 2 is a combination of bends and stretches.
Which mode is highly symmetric?
4. The symmetry elements of the molecule do not change at all with this vibration, unlike with mode 1 which, while symmetric in its vibration, changes the point group of the molecule.
One mode is known as the "umbrella" mode, which one is this?
1
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
2 bands expected. In order for a band to appear in the IR spectrum, the vibration must cause a change in dipole moment. Vibrational modes 1 and 4 do not show up in the spectrum, as their vibrations are symmetric and do not result in an overall change in dipole moment. Degenerate vibrations 2 and 3 provide one peak, as do 5 and 6. This is because their vibrations are assymmetric.
Atomic Charges
The charge on the H atoms is 0.375 and the charge on the N atom is -1.125. The negative charge on the nitrogen and the positive on the hydrogens is to be expected, as the nitrogen is more electronegative.

Nitrogen
Molecule Name: N2
Calculation Method: B3LYP
Basis Set: 6-31G(d,p)
Final Energy (au): -109.52413
RMS Gradient (au): 0.00000060
Point Group: D*H
Optimised N-N Bond Distance: 1.106 A
Item Table
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401050D-13
Optimization completed.
-- Stationary point found.
Jmol Image of Nitrogen
Nitrogen |
The optimised N2 molecule is linked here.
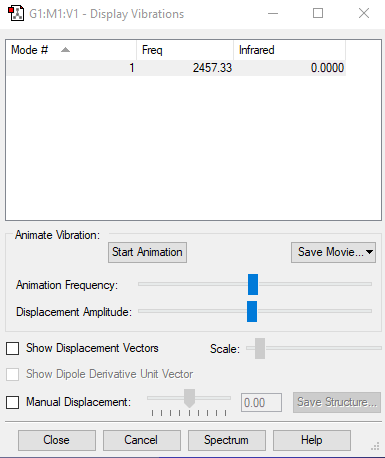
| Mode | Frequency (cm-1) | Intensity |
|---|---|---|
| 1 | 2457 | 0 |
Screenshot of the vibrational mode of nitrogen:
Atomic Charges
There is zero charge on both of the nitrogen atoms, consistant with a single-element molecule (Electonegativities of N and N are the same.)

Hydrogen
Molecule Name: H2
Calculation Method: B3LYP
Basis Set: 6-31G(d,p)
Final Energy (au): -1.17854
RMS Gradient (au): 0.00000017
Point Group: D*H
Optimised H-H Bond Distance: 0.743 A
Item Table
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
Jmol Image of Hydrogen
Hydrogen |
The optimised H2 molecule is linked here.
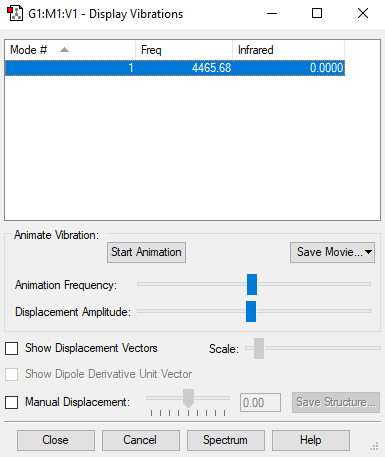
| Mode | Frequency (cm-1) | Intensity |
|---|---|---|
| 1 | 4466 | 0 |
Screenshot of the vibrational mode of hydrogen:
Atomic Charges
There is zero charge on both of the hydrogen atoms, consistant with a single-element molecule (Electonegativities of H and H are the same.)

Transition Metal Complex Containing N2 Lingands
Unique Identifier: DAMSOA
Link to the DAMSOA structure can be viewed [|here.]
N-N Bond Distances: 1.116 A and 1.117 A
The bond distance between the nitrogen atoms in the experimental result are marginally longer than those computed in Gaussian. Gaussian is limited by its base set, which cannot obtain coordinates from an infinte number of N2 structures. As well as this, electron density considered is smaller than is found experimentally. Also, Gaussian cannot compute the effects of the transition metal on the N2 ligand; something that is obviously considered with the experimental data.
The longer bond distance between nitrogens in the transition metal complex can also be accounted for using MO theory. The HOMO of the nitrogen interacts with the LUMO of the transiton metal complex. This results in the nitrogen MO losing some of its bonding character and developing more antibonding character, while the transition metal becomes more strongly bonding in character. This results in a longer bond distance in transition metal complexes compared to the N-N bond distances in pure N2.
Haber-Bosch Process
2NH3 → N2 + 3H2
E(NH3) = -56.55777 au
2E(NH3) = -113.11554 au
E(N2) = -109.52413 au
E(H2) = -1.17854 au
3E(H2) = -3.53562 au
ΔE = 2E(NH3)-[ E(N2) + 3E(H2) ] = -0.05579 au
ΔE = -146.5 kJ mol-1
The reactant of the Haber-Bosch process is slightly more stable than the products, as its energy is lower:
2E(NH3) = -113.11554 au
E(N2) + 3E(H2) = -113.05975 au
Hydrogen Sulfide
Molecule Name: H2S
Calculation Method: B3LYP
Basis Set: 6-31G(d,p)
Final Energy (au): -399.39162
RMS Gradient (au): 0.00012068
Point Group: C2V
Optimised S-H Bond Distance: 1.348 A
Optimised H-S-H Bond Angle: 92.681°
Item Table
Item Value Threshold Converged?
Maximum Force 0.000175 0.000450 YES
RMS Force 0.000145 0.000300 YES
Maximum Displacement 0.000386 0.001800 YES
RMS Displacement 0.000386 0.001200 YES
Predicted change in Energy=-1.208488D-07
Optimization completed.
-- Stationary point found.
Jmol Image of Hydrogen Sulfide
Hydrogen Sulfide |
The optimised H2S molecule is linked here.
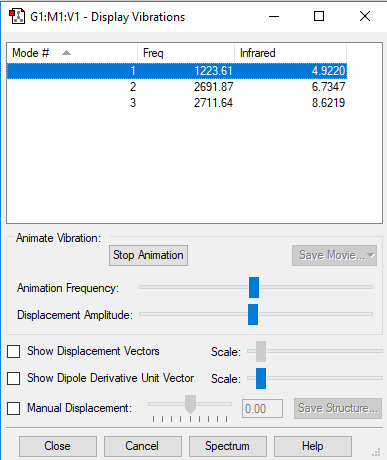
| Mode | Frequency (cm-1) | Intensity |
|---|---|---|
| 1 | 1224 | 5 |
| 2 | 2692 | 7 |
| 3 | 2712 | 9 |
Screenshot of the vibrational modes of hydrogen sulfide:
Vibtrational mode 1 is a symmetric bending vibration, mode 2 is a symmetric stretching vibration and mode 3 is an assymetric stretching vibration.
As a result, H2S will have 3 absorbance peaks in its IR spectrum, as all result in a change in dipole moment.
Atomic Charges
The more electronegative sulfur atom has a charge of -0.312, while the hydrogen atoms have a charge of 0.156.

Molecular Orbitals of Hydrogen Sulfide
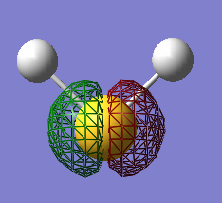
Figure 1
MO Type: Non-bonding
AO Origins: 3pz on sulfur atom
Energy (au): -5.91588
Energetic Position Relative to Other MOsː Deep
Contribution to Bondingː Insignificant (It's non-bonding)
Occupationː Two electrons, with opposite spin

Figure 2
MO Type: Sigma Bonding (gerade)
AO Origins: 1s AOs from H atoms and the 3s AO from S, all in-phase
Energy (au): -0.74654
Energetic Position Relative to Other MOsː Average
Contribution to Bondingː Significant
Occupationː Two electrons, with opposite spin

Figure 3
MO Type: Sigma Bonding (ungerade)
AO Origins: 1s AOs of opposite phase from H atoms and the 3pz AO from S. (Contributing orbitals from the S atom must be p-orbitals, as there is a clevage down the centre of the molecule.)
Energy (au): -0.44963
Energetic Position Relative to Other MOsː Average
Contribution to Bondingː Significant
Occupationː Two electrons, with opposite spin

Figure 4
MO Type: Non-bonding
AO Origins: 3px on sulfur atom
Energy (au): -0.26181
Energetic Position Relative to Other MOsː High (It's the Highest Occupied Molecular Orbital)
Contribution to Bondingː Insignificant (It's non-bonding)
Occupationː Two electrons, with opposite spin

Figure 5
MO Type: Anti-bonding
AO Origins: Out-of-phase combination of the 1s orbitals from H and the 3py S orbital
Energy (au): 0.02126
Energetic Position Relative to Other MOsː High
Contribution to Bondingː Significant
Occupationː Unoccupied (It's the Lowest Unoccpied Molecular Orbital)
Methane
Molecule Name: CH4
Calculation Method: B3LYP
Basis Set: 6-31G(d,p)
Final Energy (au): -40.52401
RMS Gradient (au): 0.00003263
Point Group: TD
Optimised C-H Bond Distance: 1.092 A
Optimised H-C-H Bond Angle: 109.471°
Item Table
Item Value Threshold Converged?
Maximum Force 0.000063 0.000450 YES
RMS Force 0.000034 0.000300 YES
Maximum Displacement 0.000179 0.001800 YES
RMS Displacement 0.000095 0.001200 YES
Predicted change in Energy=-2.256037D-08
Optimization completed.
-- Stationary point found.
Jmol Image of Methane
Methane |
The optimised CH4 molecule is linked here.
| Mode | Frequency (cm-1) | Intensity |
|---|---|---|
| 1 | 1356 | 14 |
| 2 | 1356 | 14 |
| 3 | 1356 | 14 |
| 4 | 1579 | 0 |
| 5 | 1579 | 0 |
| 6 | 3046 | 0 |
| 7 | 3162 | 25 |
| 8 | 3162 | 25 |
| 9 | 3162 | 25 |
Screenshot of the vibrational modes of methane:
How many modes do you expect from the 3N-6 rule?
3(4)-6 = 6 expected vibrational modes.
Which modes are degenerate (ie have the same energy)?
Modes 1,2 and 3, modes 4 and 5 and modes 7, 8 and 9 are degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Bond stretching modes are 7, 8 and 9. Bond bending modes are 1, 2, 3, 4, 5 and 6.
Which mode is highly symmetric?
6. The symmetry elements of the molecule do not change at all when this vibration occurs.
How many bands would you expect to see in an experimental spectrum of gaseous methane?
2 bands expected. In order for a band to appear in the IR spectrum, the vibration must cause a change in dipole moment. Vibrational modes 4, 5 and 6 do not show up in the spectrum, as their vibrations are symmetric and do not result in an overall change in dipole moment. Degenerate vibrations 1, 2 and 3 provide one peak, as do 7, 8 and 9. This is because their vibrations are assymmetric, causing a change in dipole moment.
Atomic Charges
The charge on the H atoms is 0.233 and the charge on the C atom is -0.930. The negative charge on the carbon and the positive on the hydrogens is to be expected, as the carbon is more electronegative.

Crystal Structure Containing CH4
Unique Identifier: YOSJOG01
Link to the YOSJOG01 structure can be viewed [|here.]
H-C-H Angle: 110.190°
The angle in the experimental result is marginally wider than the angle computed in Gaussian. As discussed previously, Gaussian is limited by its base set, which cannot obtain coordinates from an infinte number of CH4 structures. As well as this, electron density considered is smaller than is found experimentally. Also, Gaussian gives an angle for CH4 in its gaseous state; in the crystal it will be in the solid phase. Interactions of CH4 with the other molecules in the crystal is obviously considered in the experimental data, whereas Gaussian treats CH4 as a lone molecule.
Molecular Orbitals of Methane

Figure 6
MO Type: Non-bonding
AO Origins: 1s on carbon atom
Energy (au): -10.16707
Energetic Position Relative to Other MOsː Deep
Contribution to Bondingː Insignificant (It's non-bonding)
Occupationː Two electrons, with opposite spin

Figure 7
MO Type: Sigma Bonding
AO Origins: 1s AOs from H atoms and the 2s AO from C, all in-phase
Energy (au): -0.69041
Energetic Position Relative to Other MOsː Average
Contribution to Bondingː Significant
Occupationː Two electrons, with opposite spin

Figure 8
MO Type: Bonding
AO Origins: 1s AOs, two positive and two negative, from H atoms and the 2pz AO from C. (Contributing orbital from the C atom must be a p-orbital, as there is a node down the centre of the molecule.)
Energy (au): -0.38831
Energetic Position Relative to Other MOsː Average
Contribution to Bondingː Significant
Occupationː Two electrons, with opposite spin

Figure 9
MO Type: Bonding
AO Origins: 1s AOs, two positive and two negative, from H atoms and the 2px AO from C. (Contributing orbital from the C atom must be a p-orbital, as there is a node down the centre of the molecule.)
Energy (au): -0.38831
Energetic Position Relative to Other MOsː Average
Contribution to Bondingː Significant
Occupationː Two electrons, with opposite spin

Figure 10
MO Type: Bonding
AO Origins: 1s AOs, two positive and two negative, from H atoms and the 2py AO from C. (Contributing orbital from the C atom must be a p-orbital, as there is a node down the centre of the molecule.)
Energy (au): -0.38831
Energetic Position Relative to Other MOsː Average
Contribution to Bondingː Significant
Occupationː Two electrons, with opposite spin

Figure 11
MO Type: Bonding
AO Origins: In-phase combination of the 3s carbon AO with 4 p-orbitals, 1 from each of the hydrogens. The 3s carbon AO must be the orbital involved, as two nodal planes are clearly observable.
Energy (au): 0.11824
Energetic Position Relative to Other MOsː High
Contribution to Bondingː Significant
Occupationː Unoccupied (It's the Lowest Unoccpied Molecular Orbital)
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have recieved your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES - well organised report well done!
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES - good explanations.
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 0.5/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
This answer was incorrect, amonia is the product and has the lower energy.
Your choice of small molecule 4/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES - generally good explanations.
However you said that the LUMO has a significant contribution to bonding. This is incorrect as it is unoccupied it has no contribution. The LUMO is important when reactivity with other molecules is considered.
Independence 1/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or
YES you calculated methane.
note that the basis stes used in these types of calculations don't have anything to do with an "infinte number of CH4 structures".
Do some deeper analysis on your results so far