Rep:Mod:BMFG7519
BH3
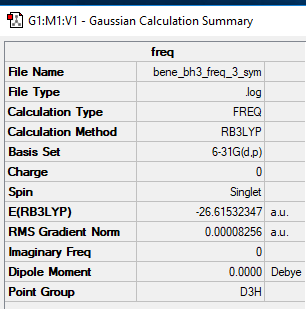
Computational Level and Basis Set: B3LYP/6-31G level
Item Value Threshold Converged? Maximum Force 0.000165 0.000450 YES RMS Force 0.000083 0.000300 YES Maximum Displacement 0.000650 0.001800 YES RMS Displacement 0.000325 0.001200 YES
Frequency analysis log file File:BENE BH3 FREQ 33 SYM.log
Low frequencies --- -0.2407 -0.1105 -0.0054 44.9603 46.0936 46.0942 Low frequencies --- 1163.6314 1213.6102 1213.6129
BH3 molecule |
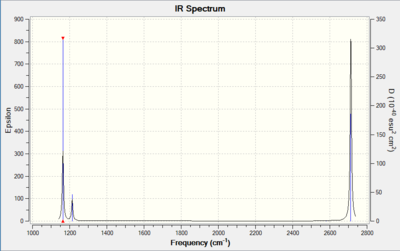
Vibrational spectrum for BH3
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1163.63 | 92 | A2" | yes | out-of-plane bend |
| 1213.61 | 14 | E' | yes | bend |
| 1213.61 | 14 | E' | yes | bend |
| 2580.06 | 0 | A1' | no | symmetric stretch |
| 2713.01 | 126 | E' | yes | asymmetric stretch |
| 2713.02 | 126 | E' | yes | asymmetric stretch |
The vibrations shown in the spectrum are only three, though the ones observed in Guassview Frequency table are six. Out of these six, the symmetrical stretch (2580.06 cm-1) is IR inactive because it does not involve a change in dipole, so disobeys the selection rules. Of the remaining five, there two sets of degenerate vibrations (1213 cm-1 and 2713 cm-1) so that out of these four we only see one signal.
Molecular Orbital Diagram for BH3
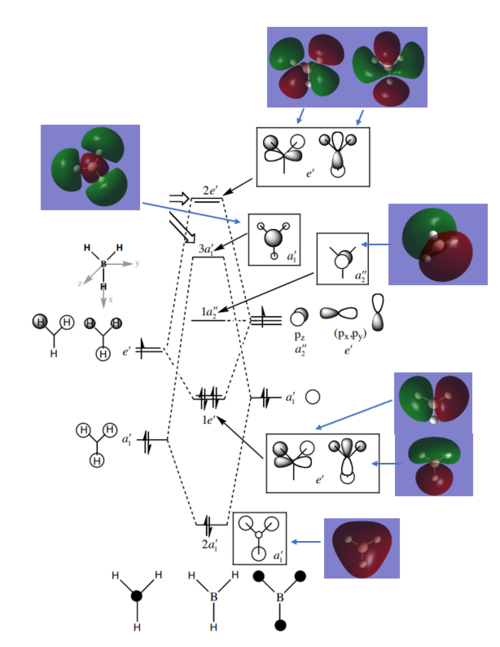
Ng611 (talk) 13:45, 17 May 2019 (BST) Good!
Questions:
Are there any significant differences between the real and LCAO MOs?
The contributions from each FOs to the MOs is more accurate in the computer. Most importantly, the computed MOs show the overall electron density of the overlap rather than simply placing the orbitals drawings on top of each other. Going up in energy, however, this makes them harder to interpret.
Ng611 (talk) 13:45, 17 May 2019 (BST) How does it make them harder to interpret exactly?
What does this say about the accuracy and usefulness of qualitative MO theory?
MO theory is very accurate in showing the actual electron density of the FOs in-phase and out-of-phase overlaps.
Association Energies: Ammonia-Borane
NH3
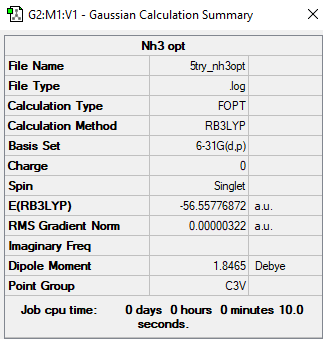
Computational Level and Basis Set: B3LYP/6-31G level
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES
Frequency analysis log file File:5TRY NH3OPT.LOG
Low frequencies --- -8.5646 -8.5588 -0.0044 0.0454 0.1784 26.4183 Low frequencies --- 1089.7603 1694.1865 1694.1865
NH3 molecule |
NH3BH3
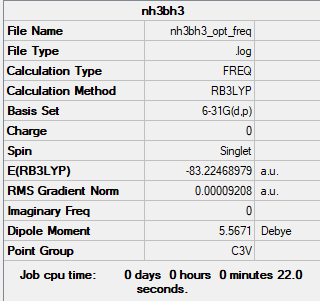
Computational Level and Basis Set: B3LYP/6-31G level
Item Value Threshold Converged? Maximum Force 0.000209 0.000450 YES RMS Force 0.000092 0.000300 YES Maximum Displacement 0.001227 0.001800 YES RMS Displacement 0.000663 0.001200 YES
Frequency analysis log file File:NH3BH3 OPT FREQ.LOG
Low frequencies --- -0.0590 -0.0428 -0.0066 23.0658 23.0711 41.6772 Low frequencies --- 265.1032 632.3076 639.8596
NH3 molecule |
Association Energy
E(NH3) = -56.55777 au
E(BH3) = -26.61532 au
E(NH3BH3) = -83.22469 au
Association Energy = ΔE =E(NH3BH3)-[E(NH3)+E(BH3)] = -83.22469 - (-56.55777 -26.61532) = -0.05160 au = -135.45 kJ/mol
Ng611 (talk) 13:47, 17 May 2019 (BST) Good answer buy you've reported your answer to too high a level of precision. With your current level of theory and basis set, your precision is about 1 kJ/mol and your values should be reported as such.
Questions
Based on your energy calculation is the B-N dative bond weak, medium or strong? What comparison have you made to come to this conclusion?
The association energy is negative, suggesting that the formation of the complex through the Boron-Nitrogen dative bond is favourable and results in energy stabilisation. Comparing the Lewis acid-base adduct strength (135 kJ/mol) to a C-C bond (90 kJ/mol) the extra stabilization can be due to the ionic contribution from the difference in electronegativities between N and B, which adds on top of the dative covalent bond.
Ng611 (talk) 13:48, 17 May 2019 (BST) Where did you get that value of the c-c bond from?
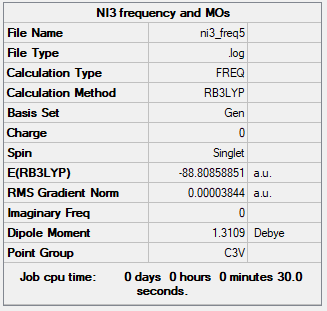
NI3
Method: B3LYP/6-31G(d,p)LANL2DZ
Item Value Threshold Converged? Maximum Force 0.000003 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000023 0.001800 YES RMS Displacement 0.000010 0.001200 YES
Frequency analysis log file File:AGAINNI3GIFFY3FREQ.LOG
Low frequencies --- -12.5522 -12.5460 -6.0047 -0.0040 0.0191 0.0664 Low frequencies --- 100.9969 100.9977 147.3377
NH3 molecule |
N-I bond lenght = 2.18396 Å
Ng611 (talk) 13:49, 17 May 2019 (BST) Again, far too precise. 3 d.p is appropriate
Ionic Liquids Mini Project
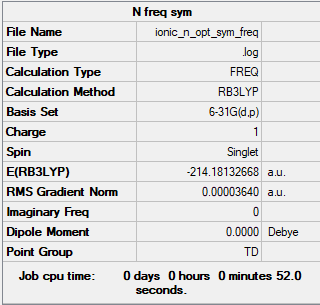
[N(CH3)4]+
Method Level: B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000072 0.000450 YES RMS Force 0.000036 0.000300 YES Maximum Displacement 0.000741 0.001800 YES RMS Displacement 0.000430 0.001200 YES
Link to log file: File:IONIC N OPT SYM FREQ.LOG
Low frequencies --- -0.0008 -0.0007 0.0002 34.4650 34.4650 34.4650 Low frequencies --- 216.5975 315.9844 315.9844
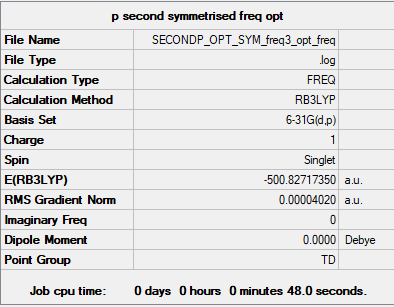
[P(CH3)4]+
Method Level: B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000080 0.000450 YES RMS Force 0.000040 0.000300 YES Maximum Displacement 0.000250 0.001800 YES RMS Displacement 0.000130 0.001200 YES
Link to log file: File:SECONDP OPT SYM FREQ3 OPT FREQ.LOG
Low frequencies --- -0.0030 -0.0024 -0.0021 50.5649 50.5649 50.5649 Low frequencies --- 188.2328 213.2320 213.2320
Charge Distribution Analysis
Charge Distribution Analysis Method: Full NBO, colour sets between -0.680 and 0.680
Charge Distribution for [N(CH3)4]+

Charge Distribution for [P(CH3)4]+

| Atom | Charge (Debye) | Electronegativity (Pauling Scale) |
|---|---|---|
| N | -0.295 | 3.04 |
| C | -0.483 | 2.55 |
| H | 0.269 | 2.20 |
| Atom | Charge (Debye) | Electronegativity (Pauling Scale) |
|---|---|---|
| P | 1.667 | 2.19 |
| C | -1.060 | 2.55 |
| H | 0.298 | 2.20 |
The differences in charge distribution are due to the different electronegativities between nitrogen and phosphorous. ΔENN-C = 0.49 ΔENP-C = -0.36
So in the P-C bond the carbon is more electonegative than the phosphorous, so it has a more negative charge density. For the N-C bond the situation is reversed, and the nitrogen has a more negative charge density. The hydrogen and carbon difference doesn't change significantly because the inductive effect of electronegativity falls quickly through bonds.
Ng611 (talk) 13:51, 17 May 2019 (BST) You should also discuss the effect of molecular symmetry.
The positive charge on the complex is spread over the whole molecule because the molecular orbital theory looks at electrons as spread throughout the complex rather than divided into the individual bonds.
MO analysis for [N(CH3)4]+
Ng611 (talk) 13:58, 17 May 2019 (BST) A general comment regarding your MO analysis. I'd annotate your LCAO diagrams with the key interactions as opposed to writing them up seperately.
1st MO
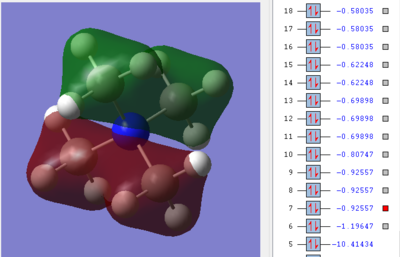
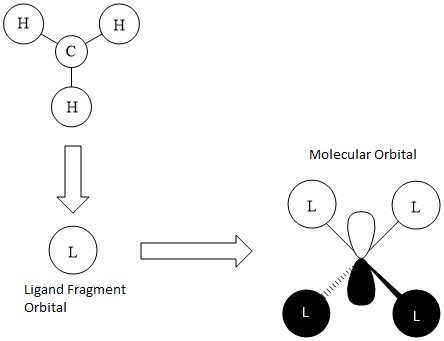
This molecular orbital is triply degenerate for the Tx, Ty and Tz symmetries in the Tetrahedral complex, which represent the three p-orbitals of the central Nitrogen atom. The only antibonding contribution is the nodal plan that passes through the N atom. This is relatively weak because it is the nature of the p-orbital. The bonding character involve: a) through-bond, directional in-phase overlaps between carbon and hydrogen s-orbitals wavefunctions; and b) through-bond in phase overlaps between the nitrogen p-orbitals and carbon s-orbitals. These sigma kind of interactions make the orbital overall bonding.
2nd MO

Ng611 (talk) 13:53, 17 May 2019 (BST) Good! You could possibly represent you FO as a p-orbital to make your diagram a little clearer.

In this triply degenerate molecular orbital, the nitrogen fragment orbital does not come into play. The nodes present that contribute to the antibonding character are based on the carbon atom: these are weaker than internuclear axis nodes, so the antibonding character is not too greatly affected. There is also through space antibonding interactions, 4 for each alkyl group = 16 in total. The bonding interactions are between the carbon p-orbital and hydrogen s-orbital, as shown by the fragment orbital of the alkyl ligand. These last are through bond and involve the strong spsigma overlap. Overall these contributions dominate and the orbital is bonding.
The absence of a contribution to bonding from the Nitrogen was unexpected: it can be rationalised by thinking that the MOs in which the nitrogen is contributing will be equal to the number of original AOs from the nitrogen. These will be the two core s-orbitals and three p-orbitals.
3rd MO
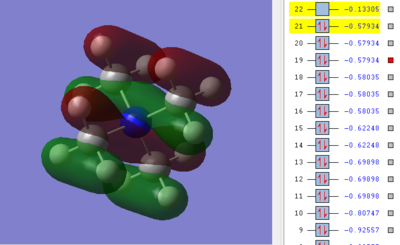
Ng611 (talk) 13:54, 17 May 2019 (BST) Good LCAO but you got the phases of your orbitals incorrect. In the calculated MO, you can clearly see delocalised systems of electrons above and below the nitrogen, suggesting a bonding interaction. As written, your LCAO predicts antibonding interactions.
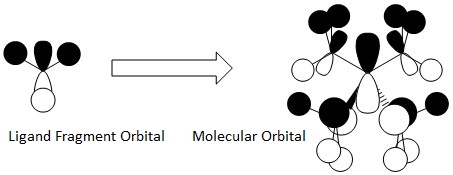
Finally, this MO is also triply degenerate, which suggests the involvement of the Tx, Ty and Tz symmetries in the Tetrahedral complex. The antibonding character is again affected by nodal planes: these are again at the atoms so not too strong. There are five nodes (on nitrogen p-orbital and four carbons p-orbitals): this increases the energy.
There is through space antibonding interactions between the hydrogen s-orbitals groups.
The bonding interactions now involve both through bond and through space. The first, stronger, are between nitrogen p-orbitals and carbon p-orbitals and between the carbon p-orbitals and s-orbitals. The bonding interactions through space are between the alkyl groups, oriented in phase.
Overall, this is still a bonding orbital.