Rep:Mod:BER1234

NH₃

Analysis of ammonia

Component	Result
Calculation method	RB3LYP
Basis set	631-G(d.p)
Final energy in a.u.	-56.5576873 a.u.
RMS gradient	0.00000485 a.u.
Point group	C3v
Optimised NH bond length	1.01798 Å
Optimised H-N-H bond angle	105.741°

Item table:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

NH3 molecule

File:BDAVIES NH3 OPTIMISATION.LOG

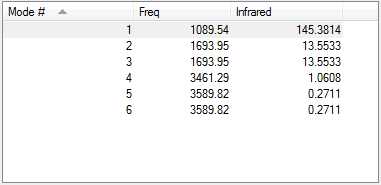
Vibration Analysis

Number of modes expected from the 3N-6 rule	6
Degenerate modes	#5 and #6, and #2 and #3
Bending vibrations	#1, #2 and #3
Bond stretch vibrations	#4, #5 and #6
Highly symmetric mode	#4
Umbrella mode	#1
Bands expected in an experimental spectrum of gaseous ammonia	2

Charge Analysis

Charge on N atom = -1.125

Charge on H atom = 0.035

I would expect a positive charge on the H atoms and a negative charge on the N atom due to nitrogen being more electronegative than hydrogen and attracting more of the electron density in the N-H bond.

N₂

Analysis of N₂

Component	Result
Calculation method	RB3LYP
Basis set	631-G(d.p)
Final energy in a.u.	-109.52412868 a.u.
RMS gradient	0.00000060 a.u.
Point group	D(inf)H
Optimised N-N bond length	1.10550 Å

Item table:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

File:BDAVIES N2 OPTIMISATION.LOG

N2 molecule

There is only one vibrational frequency: 2457.33 cm^-1

H₂

Analysis of H₂

Component	Result
Calculation method	RB3LYP
Basis set	631-G(d.p)
Final energy in a.u.	-1.17853936 a.u.
RMS gradient	0.00000017 a.u.
Point group	D(inf)H
Optimised H-H bond length	0.74279 Å

Item table:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

File:BDAVIES H2 OPTIMISATION.LOG

H2 molecule

There is also only one vibrational frequency for H₂: 4465.68 cm^-1

Energies for the Haber-Bosch Process

E(NH3) = -56.5576873 a.u.

2*E(NH3) = -113.1153746 a.u.

E(N2) = -109.52412868 a.u.

E(H2) = -1.17853936 a.u.

3*E(H2) = -3.53561808 a.u.

ΔE = 2*E(NH3)-[E(N2)+3*E(H2)] = -0.05562784 a.u. = -146.0508939 kJ/mol

Literature value for ΔE ~-50 kJ/mol^{(Prezhdo, 2016)}.

The ammonia product is more stable than the gaseous reactants.

Citation

Prezhdo, V. V. (2016). Haber Process Made Efficient by Hydroxylated Graphene: Ab Initio. The Journal of Physical Chemistry Letters.

Chosen molecule: F₂

Analysis of F₂

Component	Result
Calculation method	RB3LYP
Basis set	631-G(d.p)
Final energy in a.u.	-199.49825218 a.u.
RMS gradient	0.00007365 a.u.
Point group	D(inf)H
Optimised F-F bond length	1.40281 Å

Item table:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000128     0.000450     YES
 RMS     Force            0.000128     0.000300     YES
 Maximum Displacement     0.000156     0.001800     YES
 RMS     Displacement     0.000221     0.001200     YES

File:BDAVIES F2 OPTIMISATION.LOG

F2 molecule

There is one vibrational frequency: 1065.09 cm^-1. It is a stretch vibration. I would expect to see one band in the gaseous spectrum of flourine, corresponding to its one vibrational frequency.

There is 0 charge on each F atom, because it is a single-element molecule: therefore the electrons in the covalent bond are distributed equally.

P orbital A

Energy = -0.58753 a.u.

This is the occupied δ bonding orbital. It is formed with two P_z atomic orbitals, one from each flourine atom.

p orbital A in F₂.

P orbitals B and C

Energy = -0.52332 a.u. These are the occupied bonding pi orbitals. They are formed with one p_x and one p_y atomic orbital from each flourine atom.

p orbital B in F₂.

p orbital C in F₂.

P orbitals D and E

Energy = -0.39190 a.u. These are the occupied anti-bonding pi orbitals. They are also formed with one p_x and one p_y atomic orbital from each flourine atom. These are the HOMOs.

The LUMO is the unoccupied δ* orbital, not shown here.

P orbital D in F₂.

p orbital E in F₂.