Rep:Mod:BEARDUCKMOUSE

This computational lab uses Gaussian to investigate different features of the pericylic Diels Alder Reactions using three different examples. The molecules are analysed using either the semi-empirical PM6 method or the DFT-B3LYP method. The main difference between the both methods is the depth of the underlying approximations and consequently their computational duration. The DFT method uses a larger basis set (functions that describe electron wave-functions) in order to construct the MOs of the target molecule and comes therefore at a higher computational cost (very time consuming). From this a wide range of information can be obtained, like preferred reaction pathways, vibrational frequencies of molecules and magnetic properties to only name a few.

Last year the concept of potential energy surfaces in 3D was introduced in order to monitor the relative energies of molecules with respect to each other as a function of relative distance in space. This gave rise to saddle points (minima or maxima), each corresponding to different stages of a reaction. These stationary points have per definition a gradient of zero, and can correspond to either a transition state or a stable product. In order to differentiate between either state the curvature is taken into consideration. A negative curvature occurs when the reaction coordinate degree of freedom is the only degree of freedom not at a minimum. This is indicated as a negative frequency in the vibrational modes and shows a transition state. In contrast, a positive curvature indicates a local minimum as all degrees of freedom are minimised (locally stable product).

Good understanding of the definition of a TS, your decription is DFT is wrong. DFT modelles the energy of the system as a function of its charge density. where other methods like HF use position

Nf710 (talk) 09:49, 23 January 2017 (UTC) Your definition of a TS is somewhat miss understood, there is only a negative curvature in 1 direction, this is the cordinate in which you are going over the maximum to get to a new structure.

Exercise 1: Reaction of Butadiene with Ethylene

The reaction in investigation is a standard [4+2] Diels-Alder cycloaddition between ethylene as dienophile and butadiene as diene. The number in the brackets refer to the 4π and 2π system of butadiene and ethylene respectively. Frontier molecular orbital theory will be used to predict the MOs of the transition state and will then be compared to the computed MOs using the semi-empirical method. The PM6 optimised structures can be found here: ethylene, butadiene, TS, PRODUCT.

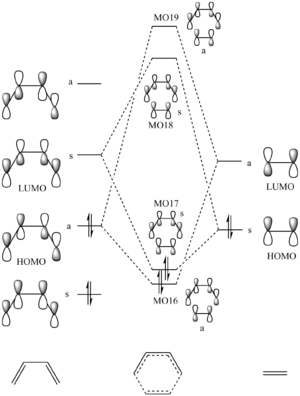
MO diagram of the cyclohexene transition structure

The MO diagram focuses on the interaction between the HOMO and LUMOs of ethylene and butadiene. The 4 fragment orbitals will result in 4 molecular orbitals of the transition state and will have to preserve symmetry. Therefore only fragment orbitals which are close in energy and of the same symmetry interact. The requirement for the latter originates that only when this condition is fulfilled there will be a non-zero orbital overlap integral, allowing the formation of the MO. This means that only symmetric/symmetric and asymmetric/asymmetric interactions are allowed.

The relative positions of the MOs of the transition state were taken from the energy calculation of the transition state. It has to be noted that MO16 and MO17 (HOMO) were very close in energy (0.001 a.u.). The fact that the interaction between the LUMO of ethylene and the HOMO of butadiene is particularly strong (more stabilised than the other interaction) leads to the conclusion that this reaction is a normal electron demand reaction (the LUMO of the dienophile should be close in energy to the HOMO of the diene).

Figure 1:MO diagram

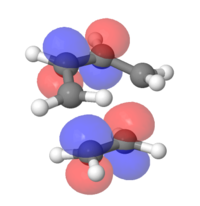
MOs for ethylene and butadiene

The MOs for both compounds were found through an energy calculation using the PM6 method. The major difference to the previous section is that the interaction between the p-orbtials is displayed within the fragment orbitals. This leads to distortions in either a constructive way (i.e. Figure 2) or in a destructive way (i.e. Figure 2.1).

Figure 2: HOMO of Ethene.

Figure 2.1: LUMO of Ethene.

Figure 3: HOMO of Butadiene.

Figure 3.1: LUMO of Butadiene

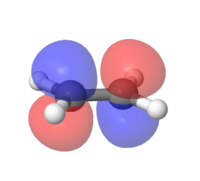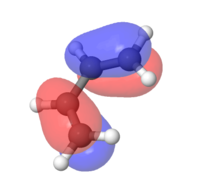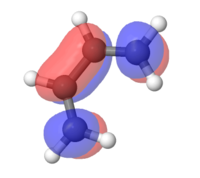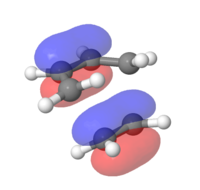
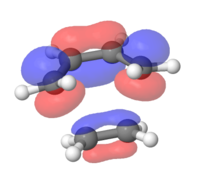
MOs for the cyclohexene transition structure

In the MOs below of the Transition Structure the symmetries are very well displayed. It shows that the HOMO and the LUMO are both symmetric (resulting from the symmetric/symmetric FO interactions) and the other two are both asymmetric (asymmetric/asymmetric FO interactions). It can be concluded that the previously proposed claim that a symmetric/asymmetric interaction will lead to a zero orbital overlap integral is correct.

Figure 4: MO 16

Figure 4.1: MO 17 (HOMO)

Figure 5: MO 18 (LUMO)

Figure 5.1: MO 19

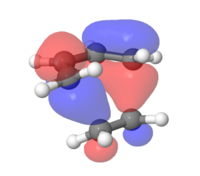Bond length analysis on this Diels-Alder Reaction

Figure 6: Reaction Scheme

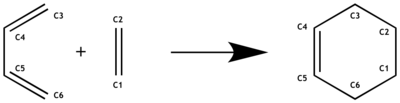The bond lengths of the bonds $C_1-C_2$, $C_3-C_4$ and $C_5-C_6$ increase as the π bonds are broken, thus reducing the strain and orbital interaction on the bond. Likewise the bond length of the bond $C_4-C_5$ decreases as a new π bond is formed. Two new σ single bonds are created between $C_2-C_3$ and $C_6-C_1$. The bond length of the transition state in those two bonds is shorter than for two C-C vdWaals radii , essentially indicating where the two molecules come together. The fact that the transition state shows that the length is the same on both bonds indicates that they are formed at the same time. This can also be seen when visualising the vibration leading up to the reaction as seen in the next section.

	Bond lengths reactants (Å)	Bond lengths transition state (Å)	Bond lengths product (Å)
$C_1-C_2$	1.327	1.382	1.541
$C_2-C_3$	no bond	2.115	1.540
$C_3-C_4$	1.335	1.380	1.500
$C_4-C_5$	1.468	1.411	1.338
$C_5-C_6$	1.335	1.380	1.500
$C_6-C_1$	no bond	2.114	1.540

Reaction path analysis using transition state vibrations

The vibration leading to the formation of the product is displayed below. As already shown through the C-C bond distances of the two molecules, the animation confirms the fact that the bond forming happens symmetrically at the same time (synchronous) on both carbon ends and was also observed by Houk et al.

An example for a non symmetric vibration is the lowest positive frequency. It can be clearly seen that the terminal carbons of the butadiene have a non-symmetrical distance to the ethylene carbons.

Nf710 (talk) 09:51, 23 January 2017 (UTC) Good first section everything very consise and easy to understand. All important parts answered.

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

The basis of the reaction is the same as the previous reaction, a [4+2] Diels-Alder cycloaddition. Reactants ( 1,3 dioxole, cyclohexadiene), Products ( endo, exo) and Transition structures ( endo TS, exo TS) were optimised to the B3LYP/6-31G(d) level. This reaction beautifully demonstrates the regioselectivity of both the exo and endo products which are controlled by the reaction trajectory and the energy pathways involved with them.

Identifying the MOs involved in the Diels-Alder reaction

The main difference between the endo and exo structure is the orientation of the 1,3 dioxole ring. In the exo structure the $C{H}_2$ end of the 1,3 dioxole points away from the double bond in the cyclohexadiene, while in the endo structure it points towards it. The HOMO and LUMO of both compounds are symmetric as a plane of symmetry can be placed through the middle of the compounds. Therefore using the Frontier Molecular Orbital Theory shows that the diagram in Figure 1 can also applied for this system as it shows that the symmetric HOMO of the dienophile interacts with the symmetric LUMO of the diene in the HOMO/LUMO region of the transition structure. Thus it must also be a normal demand Diels-Alder reaction.

(This would actually infer an inverse-demand DA. The R-O- groups on the dieneophile act as EDGs Tam10 (talk) 15:57, 3 January 2017 (UTC))

Figure 7: HOMO MO 41 of Endo Product	Figure 8: LUMO MO 42 of Endo Product	Figure 9: HOMO MO 41 of Exo Product	Figure 10: LUMO MO 42 of Exo Product

Reaction Barriers and Reaction Energies for this reaction system

The Thermal Energies, calculated Reaction Barriers and Reaction Energies are found in the table below (Figure 11). All data originates from the molecules being optimised to the DFT/B3LYP 631-G(d) level. It has to be noted that the data of the reactants was taken from their potential at infinite distance rather than using the IRC. The reason for that being that when analysing the IRC the reactant side slowly plateaued off without reaching a minimum. As can be seen below the Endo product has both the lower Reaction Barrier and the higher Reaction Energy, making it both the Kinetic and Thermodynamic product. It seems reasonable that the Endo product is the kinetic product due to stabilising secondary orbital effect (see next section) essentially lowering the reaction barrier by about 8 kJ.mol^-1. However, it is surprising to see that it is also the thermodynamic product as there are more steric clashes than in the Exo product. A possible explanation lies in the fact that it was assumed that the reactants for both reactions have the same energy, whereas in the IRC they were slightly different. Considering the difference between the products is also very small at around only 4 kJ.mol^-1 the error is big enough to lead to this unexpected result. However, also Tormena et. al. came to this result, reasoning that the attractive delocalisation interaction predominates over the steric clashes mentioned before.

	[Hartree/particle]			[kJ.mol-1]
	Reactants	Transition State	Products	Reaction Barrier	Reaction Energy
Endo	-500.391852	-500.332148	-500.418691	156.752864	70.46579
Exo	-500.391852	-500.329163	-500.417322	164.589982	66.87149
Figure 11: Thermal Energies

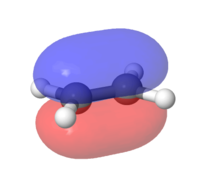
Secondary Orbital Interactions at the HOMO of the transition states

The secondary orbital effects on the Endo Transition State can beautifully seen below. The p-orbitals of the oxygens in the 1,3 dioxane interact with the π bond orbital of the cyclohexene structure. This can be seen through the "merging" of the electron clouds, essentially stabilising the molecule. Likewise this interaction does not happen in the Exo TS due to the different relative orientation in space of both molecules.

Figure 12: HOMO of Endo TS	Figure 13: HOMO of Exo TS

Nf710 (talk) 09:55, 23 January 2017 (UTC) Excellent way of shows the SOO, very good section apart form the miss understanding the oxygen not acting as EWD, as they are not carbonyls. your energies are correct and you have come to the correct conclusion.

Exercise 3: Xylylene and SO₂: Diels-Alder vs Cheletropic

This reaction can either follow the simple [4+2] Diels-Alder cycloaddition with the S-O double bond being the dienophile (leading to two products endo/exo) or a cheletropic where both bonds form on the sulphur atom. The preferred modes and drivers for each products are presented in this section. Products ( endo, exo, cheletropic) and Transition structures ( endo TS, exo TS, cheletropic TS) were optimised to the semi-empirical/PM6 level.

Animated progress of reaction for each product

As the Diels Alder reaction is now asymmetric it can be seen in the animations below that the two sigma bonds form after each other instead of synchronous. In contrast the Cheletropic system is symmetric and the vibration leading to the formation of the bond is synchronous.

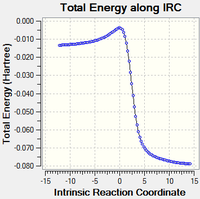Figure 14: IRC of Exo Product

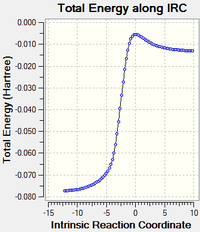Figure 15: IRC of Endo Product (reversed)

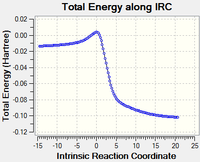Figure 16: IRC of Cheletropic Product

Energy Barriers and Reaction Energies for each product

The tabulated energies below show that both products lie very close in energy. This time the relative energy of the reactants was deduced from the IRC, leading to two slightly different values for the endo and exo system. The endo product has a lower Reaction Barrier making it the kinetic product. This can be explained through the unique reaction trajectory the SO₂ approaches the Xylylene, which is probably stabilised through secondary orbital interactions. Both products are very close in energy (about 0.1 kJ.mol^-1 difference), so that a decisive conclusion cannot be drawn. The Cheletropic product however, has a far higher activation energy but also lies far lower in energy than the other two, making it the thermodynamic product. In order to favour one product over the others in the lab, temperature and time have to be considered. I.e. a long reaction at relatively high temperature will yield a majority of the cheletropic product while a short reaction at room temperature will lead to a high yield in the endo (slightly more due to a lower AE)/exo products.

Figure 17: Reaction Scheme

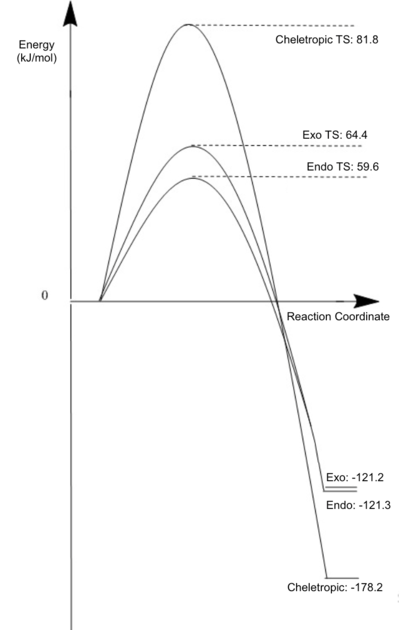(Avoid using parabolic lines for reaction profiles. They can be misleading (they also imply non-zero gradients for reactants and products). Best to just use straight, dotted lines Tam10 (talk) 15:57, 3 January 2017 (UTC))

All three reactions are strongly exothermic due to the gain of aromaticity in the carbon six ring. This is also the reason that the SO₂ is very unlikely to attack the diene inside the Xylylene six ring as the product does not result in an aromatic species. This preference towards gaining aromatic stability is also the reason why Xylylene is so unstable. It was observed in the IRC that the ring system quite easily converts to aromaticity, making it very reactive.

	[Hartree/particle]			[kJ.mol-1]
	Reactants	Transition State	Products	Activation Energy	Reaction Energy
Exo	0.067640	0.092077	0.021451	64.4218984	-121.269229
Endo	0.067837	0.090561	0.021692	59.6618665	-121.153707
Cheletropic	0.067890	0.099064	-0.000001	81.8473432	-178.247834
Figure 18: Thermal Energies

Conclusion

This lab demonstrated the power behind computational chemistry being able to determine the preferred outcome of reactions in a virtual environment using thermodynamic and molecular orbital calculations. Further research should include confirming the data obtained in the laboratory as for example the thermodynamic calculation in exercise 2 lead to some contradictions with initially expected results. It has to be noted however that those contradictions originated from the approximations used and can only really be confirmed when using methods with even higher computational cost. Another issue with the systems observed was that they were investigated in isolation, i.e. the influence of other molecules in solution were disregarded. Valuable information regarding side reactions, additional stabilisation of transition structures and additional steric hindrance were lost.