Jump to content

Rep:Mod:BC10151

From ChemWiki

NH3 Molecule

Optimisation

Optimised N-H bond distance: 1.01798 Å 

Optimised H-N-H bond angle: 105.741

Calculation Method: B3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP) in atomic units (au):-56.55776873

RMS gradient:0.00000485

Point Group: C3v

NH3

The optimisation file is linked to here

Frequency Analysis

Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
Screenshot of the "Display Vibrations" for the NH3 molecule.

How many modes do you expect from the 3N-6 rule? 3x4-6 = 6 modes


Which modes are degenerate (ie have the same energy)? Modes 2 and 3 and modes 5 and 6 are degenerate.


Which modes are "bending" vibrations and which are "bond stretch" vibrations? Bending vibrations have a lower frequency than bending vibrations, which means that modes 1 to 3 are bending vibrations whereas 4 to 6 are stretching vibrations.


Which mode is highly symmetric? Mode 4


One mode is known as the "umbrella" mode, which one is this? Mode 1


How many bands would you expect to see in an experimental spectrum of gaseous ammonia? Degenerate modes would result in a single band thus there would only be 4 bands in the spectrum.

Population Analysis

Screenshot displaying the charges of a NH3 molecule.

Charge on the N-atom:-1.125

Charge on the H-atoms:0.375

The results fit with our predictions as we would expect N to have a negative value and H to have a positive value due to the fact that N is more electronegative than H and thus would pull the electron density towards itself, resulting in a more negative charge.

H2 Molecule

Optimisation

Optimised H-H bond distance: 0.60000 Å 

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP) in atomic units (au): -1.17853936

RMS gradient:0.00000017 a.u.

Point Group:D∞h

H2

The optimisation file is linked to here

Frequency Analysis


Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES


Screenshot of the "Display Vibrations" for the H2 molecule.

N2 Molecule

Optimisation

Optimised N-N bond distance:1.09200 Å 

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP) in atomic units (au): -109.52412868

RMS gradient: 0.00000060 a.u.

Point Group:D∞h

N2

The optimisation file is linked to here

Frequency Analysis


Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES


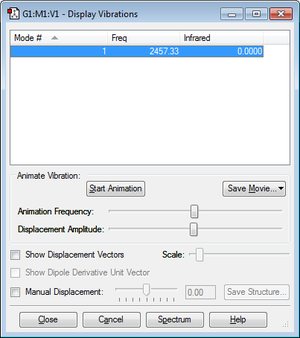
Screenshot of the "Display Vibrations" for the N2 molecule.

Determining the energy of the reaction of N2 + 3H2 -> 2NH3

E(NH3)= -56.55776873 au

2*E(NH3)= -113.1155375 au

E(N2)= -109.52412868 au

E(H2)= -1.17853936 au

3*E(H2)= -3.53561808 au

ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 au 

                          = -146.478599028 kJ/mol

We can therefore say that the ammonia product is more thermodynamically stable than the gaseous reactants as the reaction is exothermic so the product would be lower in energy than the reactants.

Project Molecule: HCl

Optimisation

Optimised H-Cl bond distance: 1.29000 Å 

Calculation Method: B3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP) in atomic units (au): -460.80077875 a.u.

RMS gradient: 0.00005211 a.u.

Point Group:C∞v

HCl

The optimisation file is linked to here

Frequency Analysis

         Item               Value     Threshold  Converged?
 Maximum Force            0.000090     0.000450     YES
 RMS     Force            0.000090     0.000300     YES
 Maximum Displacement     0.000139     0.001800     YES
 RMS     Displacement     0.000197     0.001200     YES


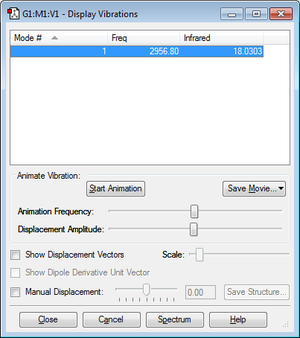
Screenshot of the "Display Vibrations" for the HCl molecule.

HCl has a single mode of vibration. This could be predicted using the 3N-5 rule, which we would use instead of the 3N-6 we used previously for NH3 because, as HCl is a linear molecule, we lose one axis of vibration. As we have 2 atoms N=2 therefore 3x2-5=1 mode. This mode corresponds to a symmetric stretching of the H-Cl bond, which would give a single band in the experimental spectrum of HCl.

The frequency of vibration of this bond could be precalculated using the following equation:

ν ˜ = 1/(2πc) √(k / μ) [1]

where ν ˜ is the wavenumber (which is the inverse of the frequency) k is the force constant (which relates to the bond strength), c is the speed of light and μ is the reduced mass, which can be calculated using the formula:

μ = m1m2/(m1+m2).

We can therefore determine that μ for HCl is 35/36, and taking k to be 481 N/m [2] , the following calculation can be carried out:

ν ˜ = 1/(2π*2.991x10^10) √[481 / (35/36)*1.66x10^-27] = 2953cm^-1, which is very similar to the value obtained from the frequency analysis.

Population Analysis

Screenshot displaying the charges of a HCl molecule.

Charge on the Cl-atom:-0.284

Charge on the H-atom:0.284

As expected, Cl has a negative value due to the fact that it is more electronegative than H, pulling the electron density towards itself. The overall sum of charges is 0 as the molecule is neutral as a whole.

Studying the Molecular Orbitals of HCl

Screenshot showing the 2s atomic orbital of Cl. This MO is very deep in energy, -9.47437 a.u., which is much lower in energy than the 1s atomic orbital of H, therefore there is no interaction between the 2s AO of Cl and the 1s AO of H.


Screenshot showing the 3s atomic orbital of the Cl atom. We can see a bit of contribution from the H atom, but this could be due to a small degree of mixing rather than a proper interaction between orbitals.


Screenshot showing the main bonding molecular orbital. This MO is the linear combination between the H 1s atomic orbital and the 3pz atomic orbital from Cl. It has an energy of -0.47433 a.u.


Screenshot showing a non bonding orbital (could either be 3px or 3py) of the Cl atom. It doesn't have the same orientation as the 1s orbital of the H atom so there is no interaction. This MO will be the HOMO, as it is the highest occupied molecular orbital.



Screenshot showing the antibonding orbital formed by the interaction between the 1s AO of H and the 3pz AO of Cl. It is very high in energy, 0.01366 a.u. This MO will be the only one unoccupied from all the given examples, and thus will be the LUMO. Higher energy MOs than this one will not have reliable shapes as the SCF procedure only optimises the occupied orbtials.


Molecular Diagram for HCl. [3]

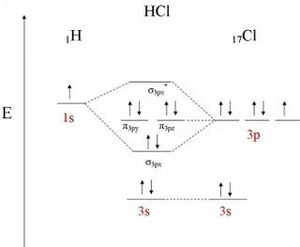
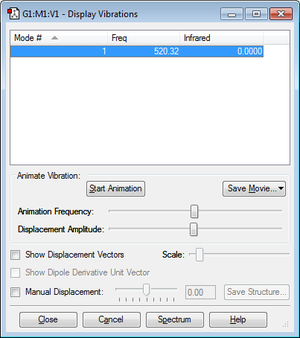
Cl2

Optimisation

Optimised Cl-Cl bond distance: 2.04174 Å 

Calculation Method: B3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP) in atomic units (au): -920.34987886 a.u.

RMS gradient: 0.00002511 a.u.

Point Group:D∞h

Cl2

The optimisation file is linked to here

Frequency Analysis

        
         Item               Value     Threshold  Converged?
 Maximum Force            0.000043     0.000450     YES
 RMS     Force            0.000043     0.000300     YES
 Maximum Displacement     0.000121     0.001800     YES
 RMS     Displacement     0.000172     0.001200     YES


Screenshot of the "Display Vibrations" for the Cl2 molecule.

References

  1. ↑ This formula was taken from the Spectroscopy and Characterisation Lecture Notes on Infra-red Spectroscopy by Charlotte Williams.
  2. ↑ This is the reference for the bond constant of the H-Cl bond.
  3. ↑ This is the reference for the Molecular Diagram of HCl.
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:BC10151&oldid=816343"