Rep:Mod:BB1916
Analysis of Formation of Ammonia (NH3)
NH3
Summary of NH3 information
- What is the molecule?
The molecule is called ammonia. It is used as a fertiliser in the whole world.
- What is the calculation method?
RB3LYP
- What is the basis set?
6-31G(d,p)
- What is the final energy E(RB3LYP) in atomic units (au)?
-56.55776873
- What is the RMS gradient (au)?
0.00000485
- What is the point group of your molecule?
C3V
- Optimal bond distance (Ångström)?
1.01798
The literature value is 1.01[1], therefore this is a good approximation.
- Optimal bond angle (degree)?
105.741
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986260D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation file is linked to here. The software used for this optimisation is called GaussView 5.0.
The "Value" approaches zero meaning the slope of distance vs energy approaches zero. The computer does not ever reach a zero value meaning that this point is the minimum energy point of the optimal bond distance.
Jmol representation of the ammonia molecule
test molecule |
Frequency
- How many modes do you expect from the 3N-6 rule?
N=4; therefore 6
- Which modes are degenerate (ie have the same energy)?
2 and 3, and 5 and 6
- Which modes are "bending" vibrations and which are "bond stretch" vibrations?
bending: 1, 2, and 3 stretching: 4, 5, and 6
- Which mode is highly symmetric?
4
- One mode is known as the "umbrella" mode, which one is this?
1
- How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
Judging from the Frequency tab you would expect 4 because there are 2 pairs of degenerate frequencies. However, upon inspecting the Infrared tab and the computer generated spectrum I considered the bandwidth of mode 4, 5, and 6 to be too narrow to be considered in an experimental spectrum.
- Thus I expect 2 bands to be observed in an experimental spectrum.
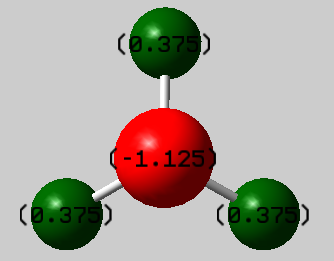
Electric Charge
Charge on H:
0.375
Charge on N: -1.125
N's Electronegativity is higher than H's, so it follows that N has a negative charge about it while H has a positive charge - compare to δ+ for H and δ- for N. Overall however the molecule is not charged which can also be seen by adding the 3 positive charges of H to the negative charge of N:
-1.125+(3*0.375)=0
N2
Summary of N2 information
- What is the molecule?
N2
- What is the calculation method?
RB3LYP
- What is the basis set?
6-31G(d,p)
- What is the final energy E(RB3LYP) in atomic units (au)?
-109.52412868
- What is the RMS gradient (au)?
0.00000060
- What is the point group of your molecule?
D∞h
- Optimal bond distance (Ångström)?
1.10550
- Optimal bond angle (degree)?
n/a due to linear structure
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401044D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation file is linked to here. The software used for this optimisation is called GaussView 5.0.
The "Value" approaches zero meaning the slope of distance vs energy approaches zero. The computer does not ever reach a zero value meaning that this point is the minimum energy point of the optimal bond distance.
Frequency
There is a frequency for stretching at 2457.33 which will not be observed in the Infrared spectrum. The atom is a linear, homonuclear structure. Thus any stretch causing any dipole would be cancelled out by the parallel nature of this molecule.
H2
Summary of H2 information
- What is the molecule?
H2
- What is the calculation method?
RB3LYP
- What is the basis set?
6-31G(d,p)
- What is the final energy E(RB3LYP) in atomic units (au)?
-1.17853936
- What is the RMS gradient (au)?
0.00000017
- What is the point group of your molecule?
D∞h
- Optimal bond distance (Ångström)?
0.74279
- Optimal bond angle (degree)?
n/a due to linear shape of the molecule.
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation file is linked to here. The software used for this optimisation is called GaussView 5.0.
The "Value" approaches zero meaning the slope of distance vs energy approaches zero. The computer does not ever reach a zero value meaning that this point is the minimum energy point of the optimal bond distance.
Frequency
There is a frequency for stretching at 4465.85 which will not be observed in the Infrared spectrum. The atom is a linear, homonuclear structure. Thus any stretch causing any dipole would be cancelled out by the parallel nature of this molecule.
Reaction Energies
All reaction energies are given in atomic units (a.u.) also known as Hartrees (defined as 2R∞hc).
3H2 + N2 --> NH3
- E(NH3)= -56.55776873
- 2*E(NH3)= -113.1155375
- E(N2)= -109.52412868
- E(H2)= -1.17853936
- 3*E(H2)= -3.53561808
- ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 a.u.
To convert the -0.0557907 a.u. to kJ/mol I employed this web converter. The converted kJ/mol value is: -35.009200289
The literature value quotes 45.94± 0.35[2]. In our course we learnt that you can try to account for more and more variables to get closer to the experimentally observed values. However, actually reaching it requires a huge computational effort which can probably not be achieved by a two-minute-long calculation.
CN-
Summary of the information
- What is the molecule?
Cyanide
- What is the calculation method?
RB3LYP
- What is the basis set?
6-31G(d,p)
- What is the final energy E(RB3LYP) in atomic units (au)?
-92.82453153
- What is the RMS gradient (au)?
0.00000704
- What is the point group of your molecule?
C∞V
- Optimal bond distance (Ångström) between C and N?
1.18409
- Optimal bond angle (degree)?
n/a due to linear shape of the molecule
I Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000005 0.001800 YES
RMS Displacement 0.000008 0.001200 YES
Predicted change in Energy=-6.650392D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1841 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The link to the optimised file is here. The software used for this optimisation is called GaussView 5.0.
Jmol representation of the cyanide molecule
test molecule |
Frequency
There is a frequency for stretching at 4465.85 which will be observed in the Infrared spectrum. As opposed to the N2 and the H2 (vide infra) this linear molecule is heteronuclear. This means they carry different charges which can also be seen in the Electric charges subsection. Therefore a measurable dipole is created in an infra-red spectrum.
Electric Charge
Charge on C:
-0.754
Charge on N: -0.246
Cyanide carries a negative charge. The negative charge is accomodated in the empty p orbital on Carbon. Thus Carbon carries the higher negative charge. But the negative charge is not -1 because Nitrogen also contributes to the negative charge.
Overall the molecule carries a singular negative charge which can also be seen by adding the charge of Nitrogen to the negative charge of Carbon:
-0.754+(-0.246)=-1
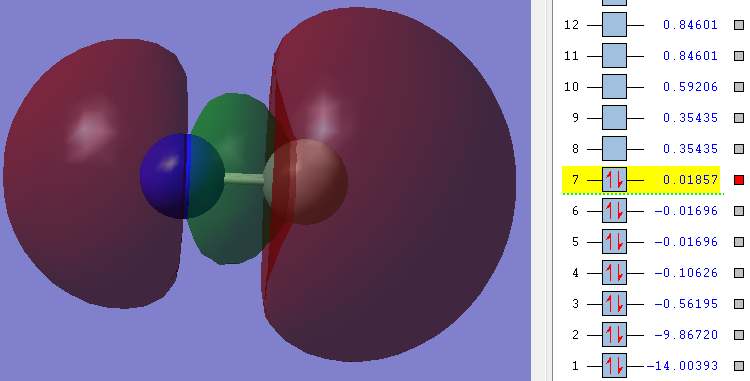
Orbitals
Carbon is grey. Nitrogen is blue.
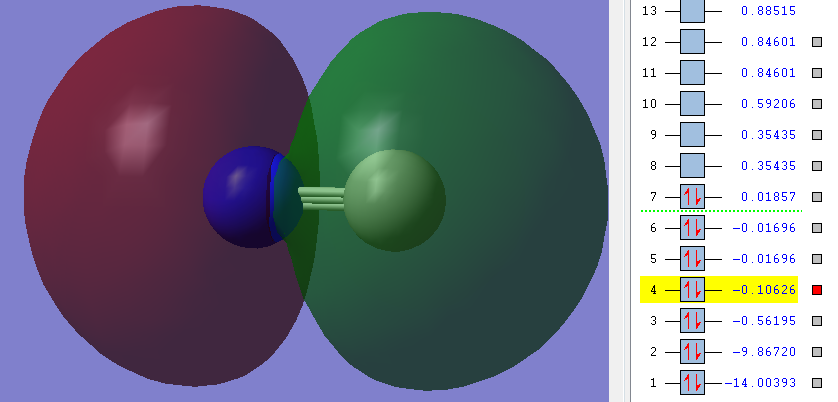
1n
As you can see in the picture the Energy of the orbitals is very low (highlighted number). Also the picture shows that there is no overlap between any orbitals, instead the orbital is exclusively around the Nitrogen.
Therefore it can be said that this is a non-bonding orbital - an orbital that does not contribute to bonding at all. It is in aspects like an equivalent of lone-pairs in the Lewis structure [3].
Nitrogen contributes both its 1s electrons to this orbital.
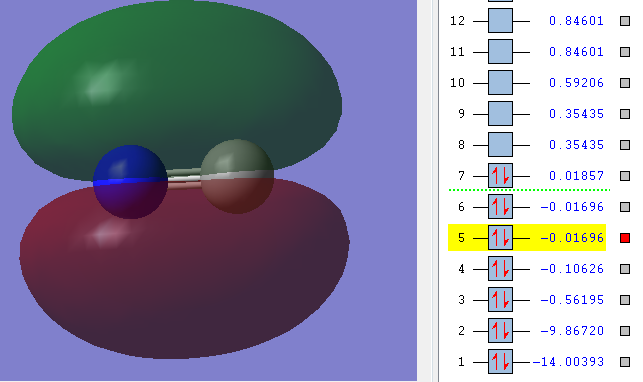
2n
As you can see in the picture the Energy of the orbitals is very low (highlighted number). Also the picture shows that there is no overlap between any orbitals, instead the orbital is exclusively around the Carbon.
Therefore this also is a non-bonding orbital[3].
Carbon contributes both its 1s electrons to this orbital.
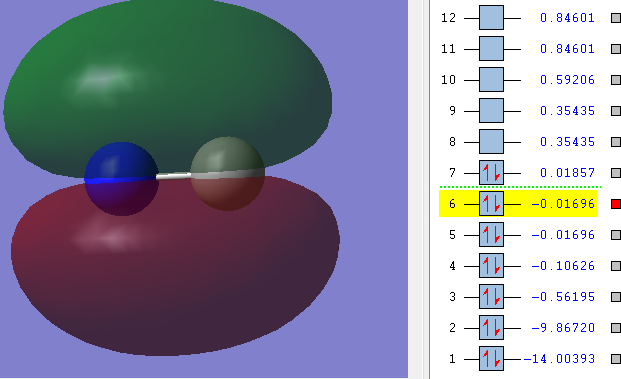
1δ
This is the first bonding orbital. It corresponds to the constructive overlap of the filled 2s orbitals of both Carbon and Nitrogen. Also the Energy (number above highlighted number) is sufficient to form an orbital. Both orbitals are in phase and exhibit circular symmetry. Therefore it results in the first bonding δ-orbital.
As you can see there is a cavity "behind" Carbon. This is due to a slight p-character contribution resulting in a node - an area with no probability of finding an electron, something δ-orbitals purely made up of s-orbitals do not exhibit.
1δ*
This is the anti-bonding orbital filled by electrons from the 2s orbitals of both Carbon and Nitrogen. There is no overlap and a node separating both electron clouds.
Both orbitals are out-of-phase and exhibit circular symmetry. Therefore it is the first anti-bonding δ*-orbital.
The electron clouds are a little skewed due to p-orbital contribution as well.
2π
This is the bonding orbital filled by the electrons from the 2px of both Nitrogen and Carbon. It is the result of the sideways overlap of the px orbitals.
Both orbitals are in-phase and exhibit a phase change when rotated about the inter-nuclear axis. Therefore it is the first bonding π orbital.
They might appear a bit rounder than normal π-orbitals due to the s-character contribution.
3π
This is the bonding orbital filled by the electrons from the 2py of both Nitrogen and Carbon. It is the result of the sideways overlap of the py orbitals.
Both orbitals are in-phase and exhibit a phase change when rotated about the inter-nuclear axis. Therefore it is the second bonding π orbital.
The bond might appear a bit rounder than normal π-orbitals due to the s-character contribution.
4δ
This is the bonding orbital filled by the electrons from the 2pz of both Nitrogen and Carbon. It is the result of the head-on overlap of the pz orbitals.
Both orbitals are in-phase and exhibit circular symmetry. Therefore it is the second bonding δ orbital.
It is the Highest Occupied Molecular Orbital.
One orbital lobe seems to be reduced while the other seems to be increased. This is due to mixing of the 1δ* orbital and this orbital. If you combined both pictures you would seem that the lobes of both orbitals with the same phase are the ones resulting in an increased orbital lobe - they are therefore constructive and the lobes of both orbitals without the same phase are the ones resulting in an decreased orbital lobe - they are therefore destructive.
The pictures I have chosen are poor because the phases of the different phases. However, phase is an arbitrary subject and can just as easily be switched.
Bond order
No other orbitals are filled therefore we have 2 non-bonding, 4 bonding and 1 anti-bonding orbitals. Subtracting the anti-bonding orbitals from the bonding orbitals results in a bond order of 3. This is in accordance with the Lewis structure.
HCN
Summary of the information
- What is the molecule?
Hydrogencyanide
- What is the calculation method?
RB3LYP
- What is the basis set?
6-31G(d,p)
- What is the final energy E(RB3LYP) in atomic units (au)?
-93.42458132
- What is the RMS gradient (au)?
0.00017006
- What is the point group of your molecule?
C∞V
- Optimal bond distance (Ångström) between C and N?
1.115702
- Optimal bond distance (Ångström) between C and H?
1.06862
- Optimal bond angle (degree)?
n/a due to linear shape of the molecule
Item Value Threshold Converged?
Maximum Force 0.000370 0.000450 YES
RMS Force 0.000255 0.000300 YES
Maximum Displacement 0.000676 0.001800 YES
RMS Displacement 0.000427 0.001200 YES
Predicted change in Energy=-2.062470D-07
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.157 -DE/DX = 0.0004 !
! R2 R(2,3) 1.0686 -DE/DX = 0.0004 !
! A1 L(1,2,3,-2,-1) 180.0 -DE/DX = 0.0 !
! A2 L(1,2,3,-3,-2) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The link to the optimised file is here. The software used for this optimisation is called GaussView 5.0.
Electric Charge
Charge on C:
-0.754
Charge on N: -0.246
Cyanide carries a negative charge. The negative charge is accomodated in the empty p orbital on Carbon. Thus Carbon carries the higher negative charge. But the negative charge is not -1 because Nitrogen also contributes to the negative charge.
Overall the molecule carries a singular negative charge which can also be seen by adding the charge of Nitrogen to the negative charge of Carbon:
-0.754+(-0.246)=-1
Comparison of Hydrogencyanide (HCN) to Cyanide (CN-)
| Cyanide | Hydrogencyanide | ||
|---|---|---|---|
| Bond distance (C-N) | 1.18409 | 1.115702 | The Bond distance between C and N decreases as you add a Hydrogen. This makes sense because the electrons are distributed over less atoms and are therefore less tightly bound. |
| Electric Charge (N) | -0.246 | -0.308 | The Electric Charge on N becomes more negative because there is no extra electron on C this time and Nitrogen's higher Electronegativity comes into play. |
| Electric Charge (C) | -0.754 | 0.073 | The Electric Charge on C becomes significantly more positive because there is no extra electron on C this time and Carbon's Electrons are spread out over 4 instead of 3 bonds. Also the Carbon is bonded to the more electronegative Nitrogen. |
| Electric Charge (H) | n/a | 0.234 | Unsurprisingly, H's charge is positive as it is bound to a more electronegative atom (C). |
| Total Charge | -1 | ~0 | All electrons are evenly distributed as you add the Hydrogen. Therefore the charge becomes approximately 0 from the original -1 which was caused by an additional electron in the system. |
| Final Energy | -92.82453153 | -93.42458132 | Cyanide is less stable than Hydrogencyanide. |