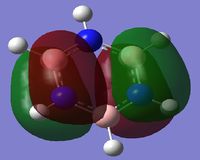
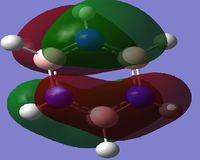
Rep:Mod:ArronDeacyproject
Aromaticity
Aromatic compounds and the phenomenon of aromaticity have both been widely studied since benzene was first isolated by Faraday in 1825. Its unusual properties has been extensively studied and the contributions from Kekule, Robinson and Huckel led to the development of 'rules' required for a molecule to be aromatic, known as the 'Huckel Rules'.
Aromatic molecules have been widely known for their increased stability compared to their non-aromatic analogues. However another useful property they exhibit is the pi-pi stacking arrangement when in liquids. This could potentially lead to a more effective way of drug design, affecting the target molecule stereochemistry, crystal packing and also affect the way proteins fold. It has also been found that large aromatic molecules have the ability to solvate carbon nanotubes which could lead to a wider application of the mechanical and electronic properties of nanotubes.[1]
The aim of this project is to understand the bonding in an aromatic compounds by computationally constructing the molecular orbitals of benzene, and to see how analogues of benzene compare in energy. It was found that by changing a C-H unit for an isoelectronic fragment, not only can the energy of the HOMOs and LUMOs be controlled but also the magnitude of the dipole moment and reactivity. This could lead to a more tailored solution for the possibilities described above.
Benzene
6-31G(d,p) Optimisation
Log file for Optimisation:Media:ArronDeacyBenzene 631G OPT.log
Dspace Link: https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25421
| File Type: .log |
| Calculation Type: FOPT |
| Calculation Method: RB3LYP |
| Basis set: 6-31G(d,p) |
| Total Energy: -232.25820551 au |
| RMS Gradient: 0.00009550 au |
| Dipole Moment: 0.00 Debye *lit: 0.001 Debye [2] |
| Point group: C1 |
| Calculation Time: 1 Minute 13.8 Seconds |
| Bond Length C-H: 1.09 Å *lit: 1.08 Å [3] |
| Bond Length C-C: 1.40 Å *lit: 1.39 Å [3] |
| Bond Angle H-C-C: 120° *lit: 120° [4] |
| Bond Angle C-C-C: 120° *lit: 120° [4] |
The bond lengths calculated by computationally solving the schrodinger equation were almost identical to the literature, as measured by electron diffraction. The bond angles calculated were 120° and is complimented by the literature. This shows that not only do all carbons in Benzene exhibit perfect sp2 hybridisation but also that our model was very good and close to the real molecule.
Item Value Threshold Converged?
Maximum Force 0.000212 0.000450 YES
RMS Force 0.000085 0.000300 YES
Maximum Displacement 0.000991 0.001800 YES
RMS Displacement 0.000315 0.001200 YES
Predicted change in Energy=-5.157444D-07
Optimization completed.
-- Stationary point found.
From this table we can see that all the forces on the molecule have converged, and a successful potential energy curve has been calculated. This is important as properties such as polarisability are sensitive to this convergence. If an optimisation is carried out and the forces have not converged then this will result in incorrect values for properties. The low RMS gradient tells us the forces exerted on a molecule at various geometries is minimal.
6-31G(d,p) Optimisation, Symmetry Restrained
Log file: Media:ArronBenzene OPT Restrained Symm.log
DSpace:https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25425
| File Type: .log |
| Calculation Type: FOPT |
| Calculation method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Total Energy: -232.25821387 au |
| RMS Gradient: 0.00008450 au |
| Dipole Moment: 0.00 Debye *lit: 0.001 Debye [2] |
| Point group: D6h |
| Calculation Time: 35.6 Seconds |
| Bond Length C-H: 1.07 Å *lit: 1.08 Å [3] |
| Bond Length C-C: 1.40 Å *lit: 1.39 Å [3] |
| Bond Angle H-C-C: 120° *lit: 120° [4] |
| Bond Angle C-C-C: 120° *lit: 120° [4] |
Item Value Threshold Converged?
Maximum Force 0.000199 0.000450 YES
RMS Force 0.000081 0.000300 YES
Maximum Displacement 0.000847 0.001800 YES
RMS Displacement 0.000299 0.001200 YES
Predicted change in Energy=-4.636845D-07
Optimization completed.
-- Stationary point found.
All forces converged therefore optimisation was successful.
Frequency Analysis
Log File: Media:ArronDeacyBenzene FREQ REST SYMM.log
DSpace: https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25429
| File Type: .log |
| Calculation Type: FREQ |
| Calculation Method: RB3LYP |
| Basis set: 6-31G(d,p) |
| Total Energy: -232.25821387 au |
| RMS Gradient: 0.00008452 au |
| Dipole Moment: 0.00 Debye |
| Point group: D6h |
| Calculation time: 1 Minute 6.1 Seconds |
Here, the energy of the molecule, both after frequency analysis and after the restrained symmetry optimisation is the same, therefore verifying that the structure and geometry of the molecule are the same.
Low frequencies --- -4.6046 -4.6046 -0.0089 -0.0043 -0.0042 9.6590 Low frequencies --- 413.9386 413.9386 621.1428
From this we can tell that the geometry is at a minima in the potential energy surface calculated by the optimisation.
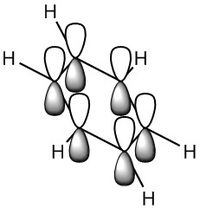
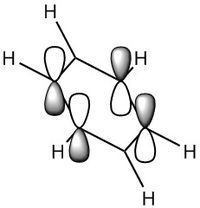
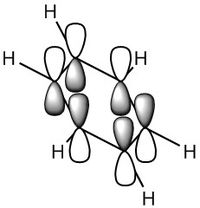
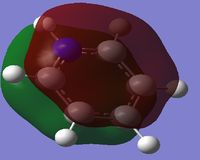
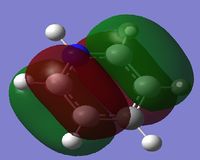
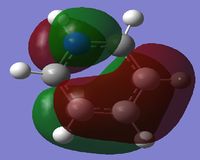
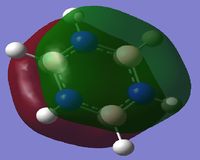
MO Diagram
For a molecule to be aromatic it must full fill three factors which are the common conceptions to aromaticity, these are; pi-conjugated ring system, planar in shape and the number of electrons must be 4n+2 where n is an integer as described by the Huckel Rule of Aromaticity.[5]
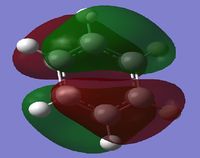
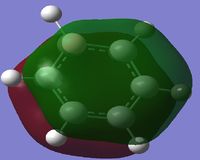
By looking at the MO diagram above for benzene, we can see that there are three bonding orbitals which are all pi-interactions. These are MO 17 (A2U) and 20/21 (E1G). Each orbital holds a maximum of two electrons and therefore the total number of pi-conjugate electrons is 6, which full fills the 4n+2 rule where n is equal to 1 in this case. From the real MO's we can see that the molecule of benzene is planar, allowing maximum conjugation between the p-orbitals for maximum delocalisation.
NBO Analysis
Log File:Media:ArronDeacyBenzene NBO.log
DSpace:https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25447
| File Type: .log |
| Calculation Type: SP |
| Calculation Method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Total Energy: -232.25821387 au |
| RMS Gradient: - |
| Dipole Moment: 0.00 Debye |
| Point Group: D6h |
| Calculation Time: 23.9 Seconds |
| Charge Range:-0.239 to +0.239 |
Full explanations of charge distribution located in the 'Comparison of Charges' section.
| Charge Distribution | Atoms | Charge |
|---|---|---|
 |
Carbon | -0.239 |
| Hydrogen | +0.239 |
Boratabenzene Anion
6-31G(d,p) Optimisation
LOG File:Media:ArronDeacyBORATABENZENE 631G OPT.LOG
| File Type: .log |
| Calculation Type: FOPT |
| Calculation Method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Charge: -1 |
| Total Energy: -219.02052937 au |
| RMS Gradient: 0.00017195 au |
| Dipole Moment: 2.85 Debye |
| Point Group: C1 |
| Calculation Time: 56 Seconds |
| Bond Length B-H: 1.22 Å |
| Bond Length B-C: 1.51 Å *lit: 1.514(2)Å [6] |
| Bond Angle C-B-C: 115° *lit: 116° [7] |
| Bond Angle C-B-H: 122° *lit: 122° [7] |
Item Value Threshold Converged?
Maximum Force 0.000432 0.000450 YES
RMS Force 0.000086 0.000300 YES
Maximum Displacement 0.001771 0.001800 YES
RMS Displacement 0.000521 0.001200 YES
Predicted change in Energy=-1.153902D-06
Optimization completed.
-- Stationary point found.
All forces have converged and so a successful optimisation has occured, producing a good potential energy surface.
6-31G(d,p) Optimisation Symmetry Restrained
Log File: Media:ArronDeacyBORATABENZENE 631G OPT SYMM.LOG
| File Type: .log |
| Calculation Type: FOPT |
| Calculation Method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Charge: -1 |
| Total Energy: -219.02052935 au |
| RMS Gradient: 0.00017367 au |
| Dipole Moment: 2.85 Debye |
| Point Group: C2v |
| Calculation Time: 42 Seconds |
| Bond Length B-H: 1.22 Å |
| Bond Length B-C: 1.51 Å *lit: 1.514(2)Å [6] |
| Bond Angle C-B-C: 115° *lit: 116° [7] |
| Bond Angle C-B-H: 122° *lit: 122° [7] |
Item Value Threshold Converged?
Maximum Force 0.000435 0.000450 YES
RMS Force 0.000086 0.000300 YES
Maximum Displacement 0.001644 0.001800 YES
RMS Displacement 0.000521 0.001200 YES
Predicted change in Energy=-1.166387D-06
Optimization completed.
-- Stationary point found.
All forces converged. Successful optimisation.
Frequency Analysis
Log File:Media:ArronDeacyBORATABENZENE 631G FREQ SYMM.LOG
| File Type: .log |
| Calculation Type: FREQ |
| Calculation Method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Charge: -1 |
| Total Energy: -219.02052935 au |
| Gradient: 0.00017367 au |
| Dipole Moment: 2.85 Debye |
| Point Group: C2v |
| Calculation Time: 45 Seconds |
Low frequencies --- -10.1896 0.0006 0.0007 0.0010 15.3919 19.2748 Low frequencies --- 371.6441 404.2296 565.3161
The energy after the frequency analysis is equal to the energy after optimisation and so the correct minima has been found for our molecule and its geometry.
NBO Analysis
Log FileMedia:ArronDeacyBORATABENZENE 631G NBO.LOG
| File Type: .log |
| Calculation Type: SP |
| Calculation Method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Charge: -1 |
| Total Energy: -219.02052935 au |
| Gradient: - |
| Dipole Moment: 2.85 Debye |
| Point Group: C2v |
| Calculation Time: 10 Seconds |
| Charge Range: -0.588 to +0.588 |
Full explanations of charge distribution located in the 'Comparison of Charges' section.
| Number Label | No. | Charge | Charge Label |
|---|---|---|---|
 |
1 | -0.250 | 
|
| 2 | -0.340 | ||
| 3 | -0.250 | ||
| 4 | -0.588 | ||
| 5 | -0.588 | ||
| 6 | +0.179 | ||
| 7 | +0.186 | ||
| 8 | +0.179 | ||
| 9 | +0.184 | ||
| 10 | +0.184 | ||
| 11 | +0.202 | ||
| 12 | -0.097 |
Pyridinium
6-31G(d,p) Optimisation
Log File:Media:ArronDeacyPYRIDINIUM OPT 631G.LOG
| File Type: .log |
| Calculation Type: FOPT |
| Calculation Method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Charge: +1 |
| Total Energy: -248.66807295 au |
| RMS Gradient: 0.00003005 au |
| Dipole Moment: 1.87 Debye *lit: 1.975 Debye [2] |
| Point Group: C1 |
| Calculation Time: 1 Minute 23 Seconds |
The Literature value for the dipole moment was for the Pyridine molecule and not specifically its cation. These values should be relatively similar due to the same molecular structure, but only differe slightly in its electron count. We can see that the numbers are similar and therefore is a good comparison.
Item Value Threshold Converged? Maximum Force 0.000037 0.000450 YES RMS Force 0.000015 0.000300 YES Maximum Displacement 0.000653 0.001800 YES RMS Displacement 0.000159 0.001200 YES Predicted change in Energy=-6.434107D-08 Optimization completed. -- Stationary point found.
All forces converged. Successful optimization
6-31G(d,p) Optimisation, Symmetry Restrained
Log File: Media:ArronDeacyPYRIDINIUM OPT 631G SYMM.LOG
| File Type: .log |
| Calculation Type: FOPT |
| Calculation Method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Charge: +1 |
| Total Energy: -248.66807396 au |
| RMS Gradient: 0.00003942 au |
| Dipole Moment: 1.87 Debye *lit: 1.975 Debye [2] |
| Point Group: C2v |
| Calculation Time: 34 Seconds |
Item Value Threshold Converged?
Maximum Force 0.000059 0.000450 YES
RMS Force 0.000022 0.000300 YES
Maximum Displacement 0.000662 0.001800 YES
RMS Displacement 0.000167 0.001200 YES
Predicted change in Energy=-6.373851D-08
Optimization completed.
-- Stationary point found.
All forces converged. Successful optimisation
Frequency Analysis
Log File: Media:ArronDeacyPYRIDINIUM FREQ 631G SYMM.LOG
| File Type: .log |
| Calculation Type: FREQ |
| Calculation Method: RB3LYP |
| Basis set: 6-31G(d,p) |
| Charge: +1 |
| Total Energy: -248.66807396 au |
| RMS Gradient: 0.00003935 au |
| Dipole Moment: 1.87 Debye |
| Point Group: C2v |
| Calculation time: 43 Seconds |
Low frequencies --- -7.0973 -0.0008 -0.0006 -0.0005 17.2679 18.3609 Low frequencies --- 392.4449 404.0598 620.4694
Total energy after frequency analysis is equal to the energy after optimisation and so the correct minima has been found on the potential energy surface for pyridinium and its optimized geometry.
NBO Analysis
Log File: Media:ArronDeacyPYRIDINIUM NBO 631G SYMM.LOG
| File Type: .log |
| Calculation Type: SP |
| Calculation Method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Charge: +1 |
| Total Energy: -248.66807396 au |
| RMS Gradient: - |
| Dipole Moment: 1.87 Debye |
| Point Group: C2v |
| Calculation Time: 11 Seconds |
| Charge Range: -0.476 to +0.483 |
Full explanations of charge distribution located in the 'Comparison of Charges' section.
| Number Label | No. | Charge | Charge Label |
|---|---|---|---|
 |
1 | -0.241 | 
|
| 2 | -0.112 | ||
| 3 | -0.241 | ||
| 4 | +0.071 | ||
| 5 | +0.071 | ||
| 6 | +0.297 | ||
| 7 | +0.292 | ||
| 8 | +0.297 | ||
| 9 | +0.285 | ||
| 10 | +0.483 | ||
| 11 | +0.285 | ||
| 12 | -0.476 |
Borazine
6-31G(d,p) Optimisation
Log File: Media:ArronDeacyBORAZINE OPT 631G.LOG
| File Type: .log |
| Calculation Type: FOPT |
| Calculation Method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Total Energy: -242.68459726 au |
| RMS Gradient: 0.00017575 au |
| Dipole Moment: 0.00 Debye |
| Point Group: C1 |
| Calculation time: 54 Seconds |
| Bond Length B-N: 1.43 Å *lit: 1.44(0.02) Å [8] |
| Bond Length N-H: 1.01 Å *lit: 1.02 Å [8] |
| Bond length B-H: 1.20 Å *lit: 1.20 Å [8] |
| Bond angle H-B-N: 121° *lit: 120° [8] |
| Bond angle N-B-N: 117° *lit: 120° [8] |
Item Value Threshold Converged? Maximum Force 0.000178 0.000450 YES RMS Force 0.000079 0.000300 YES Maximum Displacement 0.000749 0.001800 YES RMS Displacement 0.000300 0.001200 YES Predicted change in Energy=-8.695491D-07 Optimization completed. -- Stationary point found.
All forces converged therefore successful optimisation
6-31G(d,p) Optimisation Symmetry Restrained
Log File: Media:ArronDeacyBORAZINE OPT 631G SYMM.LOG
| File Type: .log |
| Calculation Type: FOPT |
| Calculation Method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Total Energy: -242.68458183 au |
| RMS Gradient: 0.00006543 au |
| Dipole moment: 0.00 Debye |
| Point Group: D3h |
| Calculation time: 35 Seconds |
| Bond Length B-N: 1.43 Å *lit: 1.44(0.02) Å [8] |
| Bond Length N-H: 1.01 Å *lit: 1.02 Å [8] |
| Bond length B-H: 1.20 Å *lit: 1.20 Å [8] |
| Bond angle H-B-N: 121° *lit: 120° [8] |
| Bond angle N-B-N: 117° *lit: 120° [8] |
Item Value Threshold Converged?
Maximum Force 0.000089 0.000450 YES
RMS Force 0.000033 0.000300 YES
Maximum Displacement 0.000249 0.001800 YES
RMS Displacement 0.000075 0.001200 YES
Predicted change in Energy=-9.603471D-08
Optimization completed.
-- Stationary point found.
All forces converged therefore successful optimisation
Frequency Analysis
Log File: Media:ArronDeacyBORAZINE FREQ 631G SYMM.LOG
| File Type: .log |
| Calculation Type: FREQ |
| Calculation Method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Total Energy: -242.68458183 au |
| Gradient: 0.00006553 au |
| Dipole Moment: 0.00 Debye |
| Point Group: D3h |
| Calculation Time: 28 Seconds |
Low frequencies --- -12.9003 -12.5774 -9.0861 -0.0110 0.0400 0.0624 Low frequencies --- 289.0932 289.1045 403.8867
Total energy after frequency analysis is equal to the optimisation therefore we have successfully found the minima in the potential energy surface for Borazine and its optimised geometry
NBO Analysis
Log File: Media:ArronDeacyBORAZINE NBO2 631G SYMM.LOG
| File Type: .log |
| Calculation Type: SP |
| Calculation Method: RB3LYP |
| Basis Set: 6-31G(d,p) |
| Total Energy: -242.68458183 au |
| RMS Gradient: - |
| Dipole Moment: 0.00 Debye |
| Point Group: D3h |
| Calculation Time: 7 seconds |
| Charge Range: -1.102 to +0.747 |
Full explanations of charge distribution located in the 'Comparison of Charges' section.
| Number Label | No. | Charge | Charge Label |
|---|---|---|---|
 |
1 | -0.077 | 
|
| 2 | +0.432 | ||
| 3 | -0.077 | ||
| 4 | +0.432 | ||
| 5 | -0.077 | ||
| 6 | +0.432 | ||
| 7 | +0.747 | ||
| 8 | +0.747 | ||
| 9 | +0.747 | ||
| 10 | -1.102 | ||
| 11 | -1.102 | ||
| 12 | -1.102 |
Comparisons
Comparisons of Charge Distribution
| Molecule | Charge Distributions on Molecules | Explainations |
|---|---|---|
| Benzene | |
Benzene has D6h symmetry and is totally symmetric. It does not have a dipole moment which is clear by the charge distribution image. All carbons are in the same environment with each other and all have the same charge number, -0.239. This is also true for the Hydrogens and have a value of +0.239. As Carbon is more electronegative than Hydrogen, it contains more of the electron density due to an inductive effect through the sigma framework. |
| Boratabenzene Anion | |
It is clear by the charge distribution image of the Boratabenzene Anion that the six fold symmetry that benzene had has now been broken and has become of C2v symmetry. It is also clear that the charge is not distributed symmetrically like benzene and so this molecule has a dipole moment, 2.85 Debye. In this molecule Boron is the more electropositive element and thus will have the most positive charge,+0.202. The Hydrogen in the B-H bond will then contain most of the electron density from that bond so will have the most negative charge of all the Hydrogens, -0.097. |
| Pyridinium | |
It is clear from the charge distribution of Pyridinium that the six fold symmetry that Benzene had has broken and is now of C2v symmetry. It can also be seen that the charge distribution is assymmetric with the negative charge more localised on the nitrogen and hence this molecule contains a dipole moment, 1.87 debye. Nitrogen is the most electronegative element in the molecule and hence most of the negative charge will be localised here, having a value of -0.467.  |
| Borazine | |
Borazine is totally symmetric like benzene, however it has half fold symmetry with its point group being D3h. As this molecule is symmetric it does not have a dipole moment. Nitrogen is the most electronegative element in this molecule and therefore the electron density will be more localised here. This is complimented by the NBO analysis as the charge on the nitrogen atoms is the most negative at -1.102. Boron is the most electropositive element in this molecule and therefore should have the least amount of electron density. This is complimented by the NBO analysis as the Boron atoms have a charge of +0.747. Due to symmetry there are two hydrogen environments, N-H and B-H. As the Hydrogens in the N-H bond are more electropositive than the nitrogen, these Hydrogens should have the most positive charge of all, giving these Hydrogens a charge value of +0.432. As for the Hydrogens in the B-H bond, the Hydrogen is slightly more electronegative than the Boron and so these Hydrogens will have the most negative charge between the Hydrogen environments, with the NBO analysis determining this hydrogen environment a value of-0.077. |
Comparison of MO's
| Molecule | MO's | ||
|---|---|---|---|
| LCAO |  |
 |
|
| Benzene |  E=-0.35999 (17) |
 E=-0.24691 (21) |
 E=-0.24691 (20) |
| Boratabenzene Anion |  E=-0.13210 (17) |
 E=-0.03497 (20) |
 E=+0.01094 (21) |
| Pyridinium |  E=-0.64064 (17) |
 E= -0.47885 (21) |
 E=-0.50847 (20) |
| Borazine |  E=-0.36130 (17) |
 E=-0.27590 (20) |
 E=-0.27590 (21) |
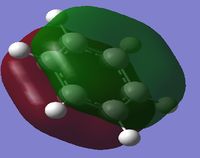
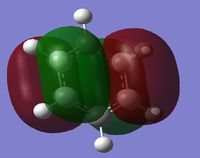
The first column of the Molecular Orbital's represents the totally bonding pi system. It is clearly seen that the orbitals are not localised to one atom, but are delocalised across a pi-conjugated system. In this Molecular Orbital (MO) there is a nodal plane lying along the carbon framework. For Benzene the orbital is the most symmetric for a p-conjugated system.
When comparing the 17th MO for the Boratabenzene Anion to the corresponding MO for Benzene, we can see that the orbital on the anion is no longer symmetric. There is less contribution from the Boron p-orbital in the LCAO and more from the lower carbon atoms, this is shown by the charge density descriptions. There is less electron density in the region surrounding the Boron as it is more electropositive than Carbon. The energy of this MO has become less negative and hence less stable compared to benzene. This is because the energy of the P orbital in boron for bonding in the conjugated system is higher due to its electropositivity and hence leads to a higher level of delocalisation. This would make the Boratabenzene Anion more reactive to aromatic substitution.
When comparing the 17th MO for Pyridinium to the corresponding benzene MO, one can again see the orbital is no longer symmetric. As Nitrogen is more electronegative when compared with Carbon, more of the orbital should be localised on the nitrogen, the size of the p-orbital in the LCAO's will be enlarged. The energy of this MO is more negative and hence more stable than the corresponding MO in benzene. This is due to the energy of the p-orbital in nitrogen being lower in energy due to its electronegativity. This reduced the amount of delocalisation and hence increased its stability, making it less reactive to aromatic substitution.
When comparing the 17th MO of borazine to the corresponding MO in benzene, it can be seen that they are very similar in the respect that they are symmetric. However, in this case more electron density is localised onto the nitrogen atoms and delocalised from the borons; the p-orbital contributions in the LCAO description will not be equal like for benzene, but the Nitrogen p-orbital will be enlarged and the Boron p-orbital will be reduced. The energy of this MO is only slightly more negative than compared with benzene and hence its reactivity to aromatic substitution should be fairly similar.
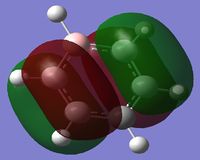
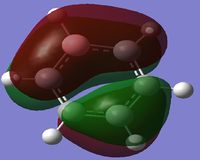
The second column of Molecular Orbital's represents the antisymmetric pi bonding system. The electron density is delocalised across 4 carbon atoms. This system contains 2 nodal planes, one in the plane of the ring and the other orthogonal crossing 2 atoms. For benzene it can be seen that the p-orbitals are symmetric and are evenly distributed amongst the 4 carbon atoms.
When comparing the 20th MO of the Boratabenzene Anion to the corresponding Benzene orbital, it is evident that the symmetry is lost. More electron density is located on the carbons furthest away from the boron in this pair (see charges summary for boratabenzene Anion). This means in the LCAO description, the p-orbital contribution from the carbons adjacent to the Boron should be slightly more enlarged than the next pair in the framework. The energy of this MO is more positive than the corresponding benzene MO. This is because the Boron is electropositive and so the carbons adjacent to the boron are more negative and so increase the amount of delocalisation into its conjugated P-orbital, hence raising its energy.
When comparing the 21st MO of pyridinium to the corresponding benzene orbital it can be seen again the symmetry is lost. Less electron density is located onto the carbons closest to Nitrogen (see charge summary for Pyridinium), leading to a lower contribution in p-orbitals compared with the next pair along in the framework. Because Nitrogen is electronegative it withdraws electron density from this MO and hence the electrons become more localised and hence lower in energy.
When comparing the 20th MO for Borazine to the corresponding benzene orbital one can see the loss in the symmetry. Most of the electron density lies on the Nitrogen as it is more electronegative, meaning the Nitrogen p-orbital will become enlarged and the Boron will be reduced in the LCAO description. There is a delocalisation factor from the Boron competing with the localisation from the Nitrogen, this change in energy is fairly even and hence the energy of this orbital is similar to that of its corresponding benzene MO.
The third column of Molecular Orbital's represents another antisymmetric pi bonding system. The electron density is delocalised across all atoms. This system also contains 2 nodal planes, one in the plane of the ring like the previous MO, however the other node orthogonal to the ring is rotated 90 degrees from the previous MO intersecting through two bonds rather than two atoms. For Benzene these MO's are orthogonal and so the sum of the overlap intergral should equate to zero. Therefore for benzene these MO's are degenerate.
When comparing the 21st MO of the Boratabenzene Anion to its corresponding benzene MO, the conjugated system for the top three atoms is not the same as the molecules on the bottom three. Boron is electropositive and therefore the adjacent carbon p-orbitals become more diffuse and delocalised and hence the orbital lobe is larger. However on the bottom the carbons p-orbital contribution is relatively similar to that of benzene. Due to the overall increase in delocalisation of the electron density, the overall energy of the MO increases compared to the corresponding benzene MO.
When comparing the 20th MO of Pyridinium to its corresponding benzene MO, the opposite effect of what was seen for the Boratabenzene Anion is observed. The Nitrogen has contracted the p-conjugation system between -(C-N-C)- and localisation of the electron density is clearly seen. Due to this localisation the molecule becomes lower in energy and hence more stable than the similar benzene MO.
When comparing the 21st MO of Borazine to its corresponding benzene MO, again there is this effect of localisation of electron density caused by the nitrogen vs delocalisation of electron density caused by the Boron. This ultimately cancels out the total energy change of the molecule and so this has a relatively similar energy to the benzene MO. Due to symmetry, the 20 and 21st MO of Borazine are degenerate.
For all analogues of benzene the totally bonding p-conjugated MO is the molecules 17th MO. For Benzene and Borazine the 20th and 21st MO's are degenerate due to symmetry. Because the Boratabenzene Anion and Pyridinium have a lower fold in symmetry, this is not the case. For the Boratabenzene Anion the two p-orbital conjugated system is the 20th MO. This is because the Boron is not directly contributing to the overall electron density, and so delocalisation is minimal. Whereas in its 21st MO the Boron is substantially increasing delocalisation and hence a higher energy is seen. For Pyridinium this is the opposite. The two p-orbital conjugated system is the 21st MO as the Nitrogen is not directly contributing to the electron density and so localisation is minimal. However in its 20th MO, it is clear the nitrogen has a strong localising effect and hence a lower energy is calculated.
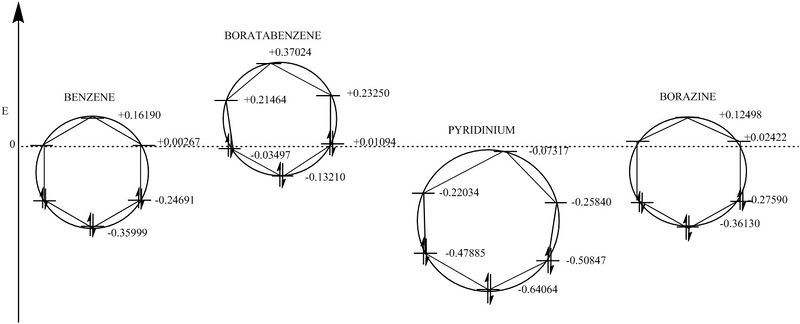
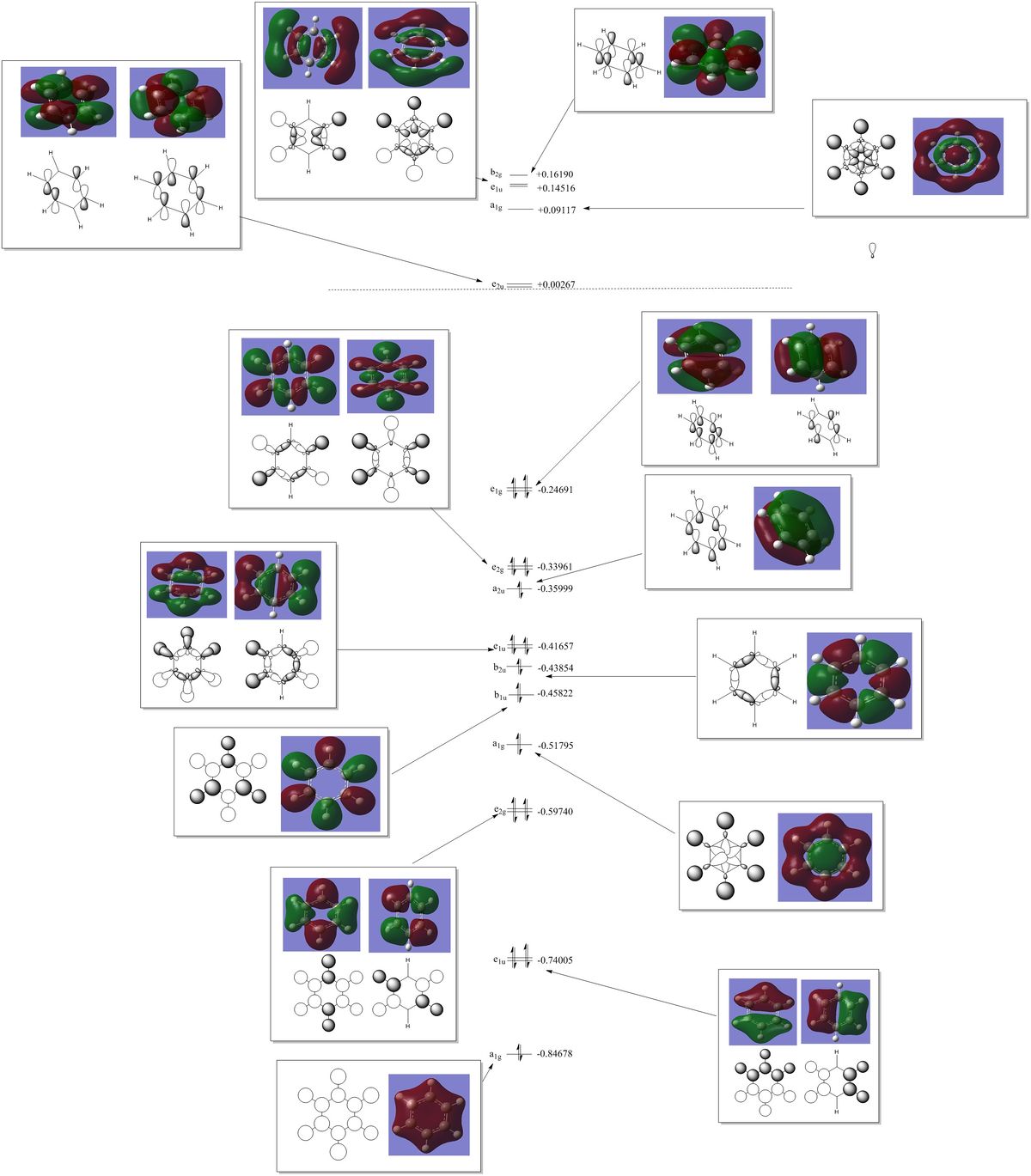
Here is a picture of how the pi-bonding MO's have changed in energy relative to benzene. It can been clearly seen that the total pi-bonding energy of the Boratabenzene Anion has increased and so this molecule should be more reactive. One can deduce that the total pi-bonding energy of Pyridinium has decreased compared to Benzene and so will be less reactive. Finally, the energy of benzene and borazine are fairly equal and so should show similar aromatic reactivity. It can also be seen here the symmetry of benzene and borazine, and how that is broken when looking at the Boratabenzene Anion and Pyridinium. We can also see that there is a difference is 'skew' between the Boratabenzene Anion and Pyridinium. The Boratabenzene anion skews to the left, and Pyridinium skews to the right suggesting a re-ordering of MO's which was explained earlier.
Conclusion
This project was to computationally compare the molecule Benzene and its analogues; the Boratabenzene anion, the Pyridinium cation and Borazine. Optimisations were made for each molecule using the 6-31G(d,p) basis set, with the symmetry restrained. Once a successful optimisation was confirmed by convergence of the forces, a frequency analysis was carried out. This was to confirm that a minima has been reached in the potential energy surface created by the 6-31G(d,p) basis set. This means the energy of the molecule after optimisation and the frequency analysis should be equal. Natural Bond Orbital (NBO) analysis was then carried out for each molecule. From there, information on the charge distribution of the molecules was obtained and each analogue was compared to Benzene. It was found that the Benzene and Borazine molecules had a symmetric charge distribution and hence did not have a dipole moment. It was also found that the Boratabenzene Anion and Pyridinium had an asymmetric charge distribution which accounted for its dipole moments, these two analogues had opposite charge distribution trends. The MO's of each molecule were also obtained from the NBO Analysis, in which a full MO diagram for Benzene was drawn showing the sigma and pi interactions, not including the 'core' MO's as these are too low down in energy to interact. The pi-bonding MO's for each analogue was calculated and compared to Benzene. It was found that the Boratabenzene Anion was slightly higher in energy, with its valence MO being +0.25785 higher in energy than benzene due to increased delocalisation of the electrons. The Pyridinium was found to be -0.23164 lower in energy than with Benzene. This was due to the increase in localisation of the electrons. The Borazine was found to be relatively similar in energy with Benzene, with its valence MO being -0.02899 lower in energy. This was due to the competing effects of localisation of electron density by the Nitrogen vs the delocalisation of electron density by the Boron.
Further Studies
- From the results reported from this project we can see that the HOMO and LUMO energies can be controlled. By adding B-H units in place of C-H we can increase the energy and by adding N-H we can decrease the energy. A further investigation could add more B-H units until (BH)6 is reached and add more N-H units until (NH)6 is reached. From these points we can then work backwards adding N-H units to (BH)6 and B-H units to (NH)6 and plot the energies observed. The following graph is a prediction of the further study results.
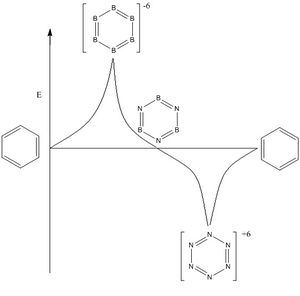
From there we can then substitute further units for the C-H unit such as P-H, S-H, Si-H. Not only can the C-H units be substituted but also the Hydrogens can be chaged to see the effects of electron withdrawing groups, electron donating groups and sterically hindered groups, this will created a more continuous energy graph allowing for better control of the HOMO-LUMO energies.
References
- ↑ S.Glanzer; A.Sax, Molecular physics: An International Journal at the interface between Chemistry and Physics, 2013, 111, 2427-2438
- ↑ 2.0 2.1 2.2 2.3 D.Lewis; M.Bird; D.Parke, Toxicology, 1997, 118, 93-113
- ↑ 3.0 3.1 3.2 3.3 H.Preuss; R.Janoschek, j. mol. struct. 1969, 3, 423-428 Cite error: Invalid
<ref>tag; name "one" defined multiple times with different content - ↑ 4.0 4.1 4.2 4.3 J.Trotter, tetrahedron, 1960, 8, 13-22
- ↑ J.Clayden, N.Greeves, S.Warren, P.Wothers, Organic Chemistry, Oxford University Press, Oxford, 8th edn, 2009
- ↑ 6.0 6.1 R.M.Minyaev; V.I.Minkin; A.G.Starikov; T.N.Gribanova, Russ. Chem. B+, 2001, 50, 2325-2335
- ↑ 7.0 7.1 7.2 7.3 D.Hoic; W.Davis, G.Fu; J. Am. Chem. Soc, 1995, 117, 8480-8481
- ↑ 8.00 8.01 8.02 8.03 8.04 8.05 8.06 8.07 8.08 8.09 S.Bauer, J. Am. Chem. Soc, 1938, 60, 524-530