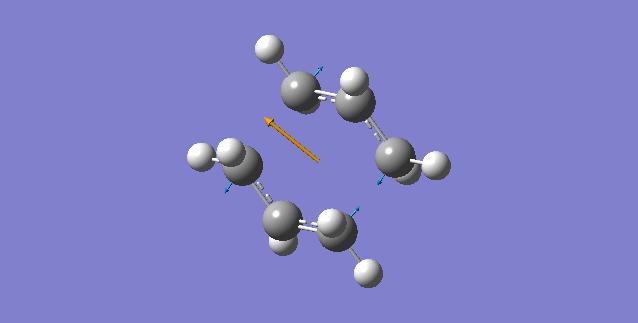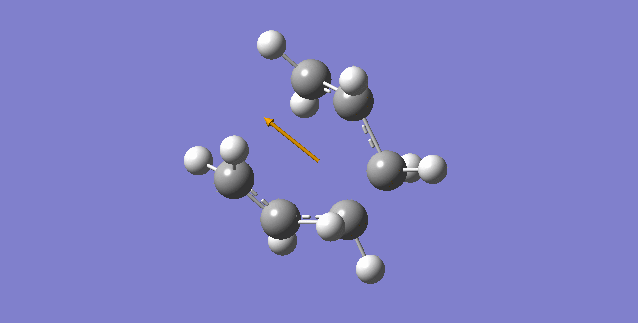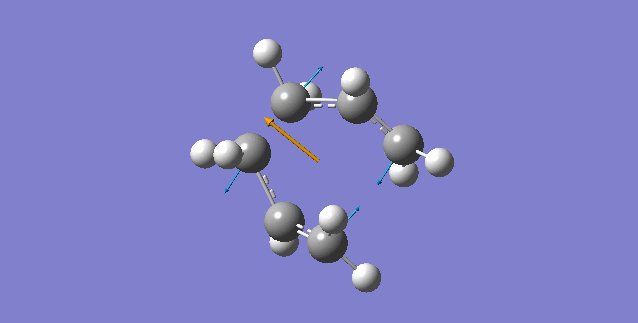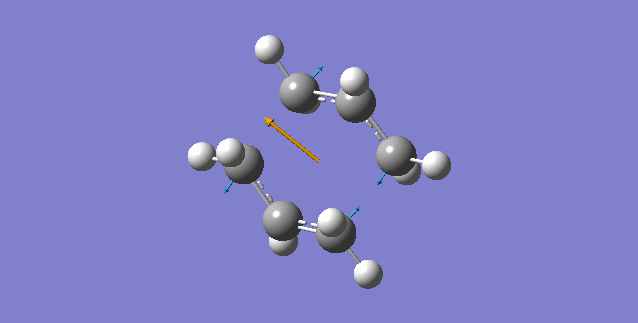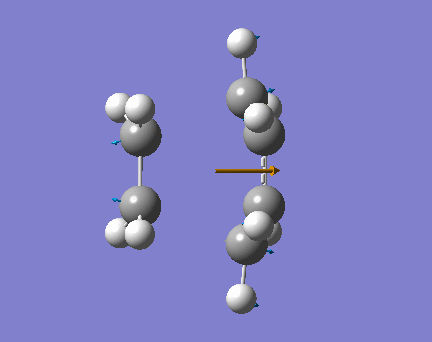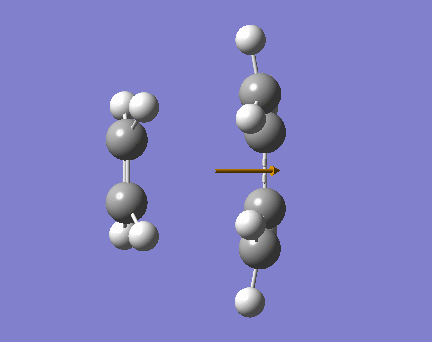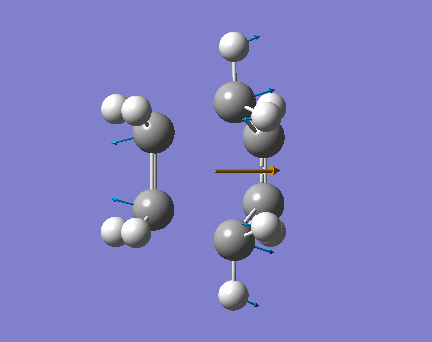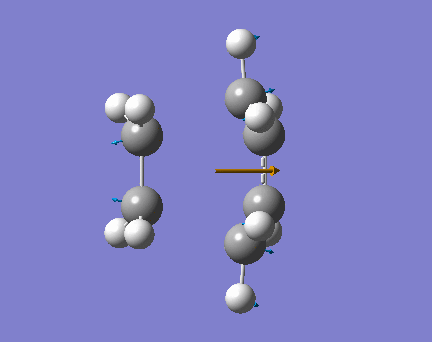Rep:Mod:ArielC

Mod: phys 3 - Transition states and reactivity

Pericyclic reactions widely occur in many organic synthesis routes and biological processes. The reactions usually progress in a concerted way with cyclic transition states and normally involve large molecules with different structures and characters. Thus, quantitative investigations of  transition structures on potential energy surfaces become important.

In this set of computational labs, the transition structures on potential energy surfaces of two typical pericyclic reactions, the Cope rearrangement and Diels Alder cycloaddition reactions, will be characterised. We know that the molecular mechanics / force field methods can be used for determining the molecular structures. However these methods are no longer (in general) working for this experiment as they do not describe bonds being made and broken, and changes in bonding type / electron distribution. Therefore, another method has been introduced in this experiment in order to investigate the structures of transition states.  Molecular orbital-based methods numerically solve the Schrodinger equation and locate transition structures based on the local shape of a potential energy surface. It shows what transition structures look like. Reaction paths and barrier heights can also be calculated.

Example A: The Cope Rearrangement

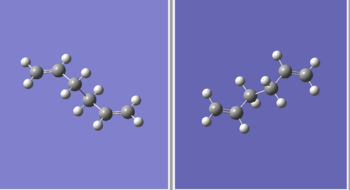
The Cope Rearrangement reaction involves the [3,3]-sigmatropic rearrangement of 1,5-dienes. The mechanisms of Cope rearrangement of 1,5-hexadiene is shown below. The reactions are usually characterized as a concerted reactions with either a "chair" or a "boat" transition structure..

Optimizing the Reactants and Products

(a).Optimization of an Anti-Peri Planar Conformer of 1,5-Hexadiene(anti 1)

First, the structure was optimized at the HF/3-21G level of theory in order to find out the relative total energy.

1.Optimized structure of anti 1,5-Hexadiene

test molecule

2.General Information of Results

Gaussian Calculation Summary

Type of Conformer	Anti 1
Job type	Optimization to a minimum
Basis Set	3-21G
Spin	Singlet
Total Energy	-231.69260236 a.u.
RMS Gradient Norm	0.00001220 a.u.
Current point group	C2

3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000034     0.000450     YES
RMS Force                0.000007     0.000300     YES
Maximum Displacement     0.001018     0.001800     YES
RMS Displacement         0.000266     0.001200     YES
Predicted change in Energy = -1.412689D-08
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

4.File Link

To access the .log file of optimization, click here.

(b).Optimization of a Gauche Conformer of 1,5-Hexadiene(Gauche 4)

1.Optimized structure of Gauche 1,5-Hexadiene

test molecule

2.General Information of Results

Gaussian Calculation Summary

Type of Conformer	Gauche 4
Job type	Optimization to a minimum
Basis Set	3-21G
Spin	Singlet
Total Energy	-231.69153029 a.u.
RMS Gradient Norm	0.00002371 a.u.
Current point group	C2

3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000034     0.000450     YES
RMS Force                0.000014     0.000300     YES
Maximum Displacement     0.001305     0.001800     YES
RMS Displacement         0.000546     0.001200     YES
Predicted change in Energy = -6.363816D-08
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

4.File Link

To access the .log file of optimization, click here.

5.Comparison with (a)

Total Energy(a)	Total Energy(b)	Total Energy difference(a)-(b)
231.69260236 a.u.	231.69153029 a.u.	0.00107207 a.u.

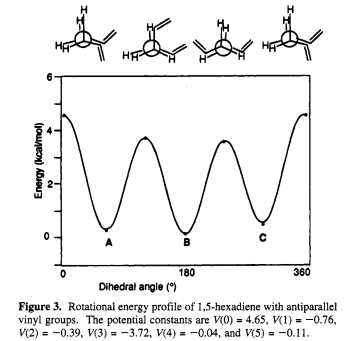
Normally, the anti conformation is energetically more stable than the Gauche conformation. This is due to the R groups being the farthest away from each other in the molecule that avoids the Van der Waals strain between those two groups. Both structures are shown below in Newman Projections:

Newman projection of anti and Gauche conformers.

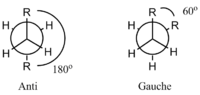
As expected,the experimental final energy of the optimized structure with gauche linkage is slightly higher than that with anti linkage due to the more hindered substituents. The energy difference is equal to 0.00107207 a.u.(or 0.672723925 kcal/mol). The energy diagram of different types of conformers of butane is drawn below. It is clearly shown the most stable structure is the anti conformation in which the two methyl groups are as far apart as possible.

Nf710 (talk) 12:08, 11 February 2016 (UTC) Did you do this on chembio? Its a nice diagram

Optimization of a Gauche Conformer of 1,5-Hexadiene(Gauche 3)

1.Optimized structure of Gauche 1,5-Hexadiene

test molecule

2.General Information of Results

Gaussian Calculation Summary

Type of Conformer	Gauche 3
Job type	Optimization to a minimum
Basis Set	3-21G
Spin	Singlet
Total Energy	-231.69266121 a.u.
RMS Gradient Norm	0.00000972 a.u.
Current point group	C1

3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000035     0.000450     YES
RMS Force                0.000007     0.000300     YES
Maximum Displacement     0.000859     0.001800     YES
RMS Displacement         0.000253     0.001200     YES
Predicted change in Energy = -1.309861D-08
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

4.File Link

To access the .log file of optimization, click here.

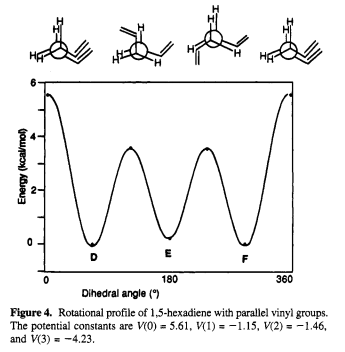
In this case, the experimental final energy of the optimized structure with gauche 3 linkage gives anomaly result, which is slightly lower than that with anti(a) linkage. This might be resulted from the π-π interaction between eclipsing 1,2-divinyl groups. The π-π interaction gives extra stablization towards the Gauche conformer so that they cause less steric strain than eclipsing 1,2-dimethyl groups in butane molecule. Comparison diagrams that matches the experimental data were drew by Benjamin W. Gung are shown below.

As shown in Figure 4, the Gauche conformers D and F are slightly more stable than the anti conformers E according to calculations at the HF/3-21G level. The Gauche form C is ~0.6 kcal/mol higher in energy than the anti form B that perfectly matched the case (a) and (b) while the experimental data is 0.672723925 kcal/mol. Therfore, according to the graph and experimental calculation, Gauche 3 conformer is likely to be the lowest energy conformer of 1,5-hexadiene.

Optimization of an anti Conformer of 1,5-Hexadiene(anti 2)

1.Optimized structure of anti 1,5-Hexadiene

test molecule

2.General Information of Results

Gaussian Calculation Summary

Type of Conformer	Anti 2
Job type	Optimization to a minimum
Basis Set	3-21G
Spin	Singlet
Total Energy	-231.69253530 a.u.
RMS Gradient Norm	0.00000847 a.u.
Current point group	Ci

3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000029     0.000450     YES
RMS Force                0.000005     0.000300     YES
Maximum Displacement     0.000476     0.001800     YES
RMS Displacement         0.000138     0.001200     YES
Predicted change in Energy = -3.404833D-09
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

4.File Link

To access the .log file of optimization, click here.

Reoptimization of an anti Conformer of 1,5-Hexadiene(anti 2)

In this session, the structure was reoptimized with a more accurate method and basis set, B3LYP/6-31G(D), in order to investigate a more precise minimum energy.

1.Reoptimized structure of anti 1,5-Hexadiene

test molecule

2.General Information of Results

Gaussian Calculation Summary

Type of Conformer	Anti 2
Job type	Optimization to a minimum
Basis Set	6-31G(D)
Spin	Singlet
Total Energy	-234.61171164 a.u.
RMS Gradient Norm	0.00002282 a.u.
Current point group	Ci

3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000082     0.000450     YES
RMS Force                0.000013     0.000300     YES
Maximum Displacement     0.000974     0.001800     YES
RMS Displacement         0.000299     0.001200     YES
Predicted change in Energy = -2.325878D-08
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

4.Frequency Calculations

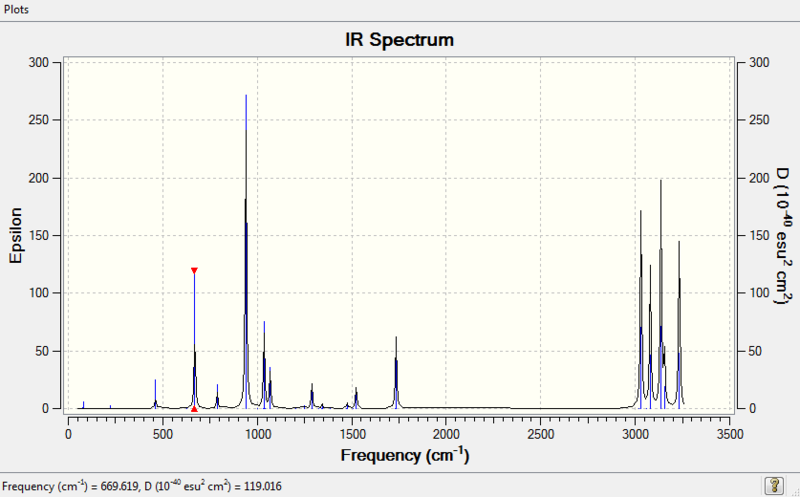
Frequency calculations were carried out at the same level of theory(B3LYP/6-31G(D)). The frequency calculations show that all vibrational frequencies are positive and real in the range from 73.92cm^-1 to 3233.11cm^-1. This confirms a minimum in this case.

5.IR Spectrum

There are several vibrations on the vibrational frequency table that have zero IR absorption intensity and thus can not be found on the IR spectrum. This is because the high symmetry Ci of (anti 2)1,5-hexadiene, leading to the lack of dipole moment of some particular vibrations that are IR active. The calculated IR spectrum may also differ with experimental data. As Gauche structures and anti structures interchange in a very short period of time, most of the IR machines cannot distinguish two conformers in reality. The experimental IR spectrum generally gives 'average' frequencies of the mixture of all conformers. An experimental spectrum of 1,5-hexadiene can be found from this website and a digitized version is shown below.

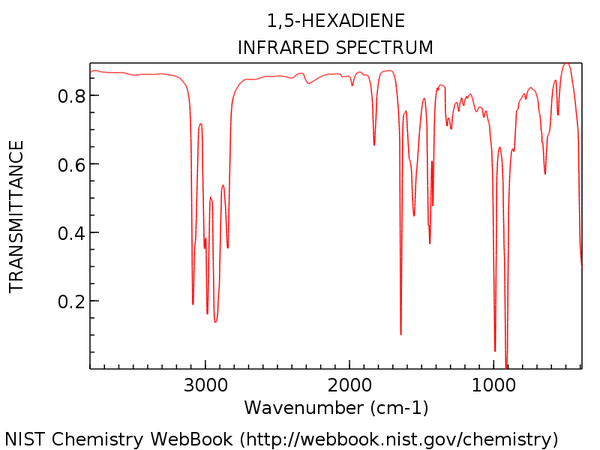
Comparing those two IR spectrum above, some shifts of vibrational peaks can be found. This might be resulted from the difference in temperature. The calculations of frequencies in Gaussion were carried out at 298.15K and 1 atm of pressure while the real temperature and pressure of the experimental spectrum may actually differ. Moreover, the experimental spectrum was operated long time ago which based on the old techniques. Nowadays, the accuracy of IR spectrometer has certainly enhanced. It might be possible to distinguish the Gauche and anti conformers using modern techniques.

6.File Link

To access the .log file of reoptimization, click here. To access the .log file of frequency calculation, click here. To view the screenshot of the vibration frequency table, click here

Nf710 (talk) 12:12, 11 February 2016 (UTC) You havent done a geometry calculation

Nf710 (talk) 12:18, 11 February 2016 (UTC) Good comparison to literature

Results and discussion

1.Geometry Analysis

The structures of molecules after optimization at different levels and corresponding bond lengths with bond angles are shown below:

	HF/3-21G	B3LYP/6-31G(d)
Structure	test molecule	test molecule

Geometric Parameter           HF/3-21G          B3LYP/6-31G(D)    
C1=C2 Bond Length/Å            1.31614           1.33351     
C2-C3 Bond Length/Å            1.50883           1.50405     
C3-C4 Bond Length/Å            1.55292           1.54820     
C1=C2-C3 Bond Angle            124.81087o        125.30310o     
C2-C3-C4 Bond Angle            111.34677o        112.67126o
C2-C3-C4-C5 Dihedral Angle     179.99381o        179.99657o

The overall change of geometry is small. The large energy difference between those two calculations might be resulted from the change of dihedral angle of C₂-C₃-C₄-C₅. At B3LYP/31G(D)level, the C=C double bond has better alignment with adjacent carbon-carbon or carbon-hydrogen bond. This leads stronger σ-π conjugation and large stabilization energy. In general, the B3LYP/6-31G(D) method is more accurate than the HF/3-21G method as the optimized angles and bong lengths are closer to the real experimental values..

2.Thermochemistry

Type of energy/a.u.                                      HF/3-21G          B3LYP/6-31G(D)   
1.Sum of electronic and zero-point Energies              -231.539540       -234.469214
2.Sum of electronic and thermal Energies                 -231.532566       -234.461867
3.Sum of electronic and thermal Enthalpies               -231.531622       -234.460923
4.Sum of electronic and thermal Free Energies            -231.570915       -234.500796

• The first is the potential energy at 0 K including the zero-point vibrational energy (E = E_elec + Z_PE).
• The second is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + E_vib + E_rot + E_trans).
• The third contains an additional correction for RT (H = E + RT) which is particularly important when looking at dissociation reactions.
• The last includes the entropic contribution to the free energy (G = H - TS).

It is meaningless to compare the energy of different levels of theory as the energy difference is relatively large. The B3LYP/6-31G(D) method is more accurate which gives relatively lower electronic energy comparing with the HF/3-21G method. This indicates the larger stabilization energy resulting in more stable structure.

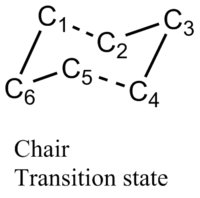
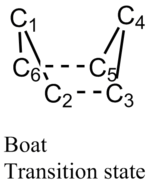
Optimizing the "Chair" and "Boat" Transition Structures

The "chair" and "boat" transition state structures for the cope rearrangement reaction are both consist of two C₃H₅ allyl fragments, with C_2h symmetry and C_2v symmetry respectively. The transition structures are shown below,

Chair transition stucture(C_2h)

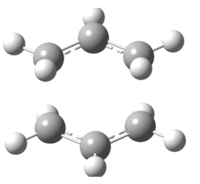
Boat transition stucture(C_2v)

Optimization of Allyl Fragment

1.Optimized structure of Allyl

test molecule

2.General Information of Results

Gaussian Calculation Summary

Name of molecule	Allyl fragment
Job type	Optimization to a minimum
Basis Set	3-21G
Spin	Doublet
Total Energy	-115.82304010 a.u.
RMS Gradient Norm	0.00001656 a.u.
Current point group	C2v

3.File Link

To access the .log file of optimization, click here.

a.Optimization at HF/3-21G level using Berny Algorithm method

This method only works well when a reasonable guess for the transition structure geometry has been made. It computes yje force constant matrix in the first step of the optimization which will then be updated as the optimization proceeds. This method effectively shortens the optimization time. However, it might not give precise result depending on how good is the approximation of the transition state structure.

1.Optimized structure of Chair Transition state

test molecule

2.General Information of Results

Gaussian Calculation Summary

Name of molecule	Chair Transition states structure
Job type	Optimization to a TS(Berny)
Basis Set	3-21G
Spin	Singlet
Total Energy	-231.61932245 a.u.
RMS Gradient Norm	0.00001339 a.u.
Current point group	C2h
Number of Imaginary Frequency	1
Magnitude of Imaginary frequency	-817.96 cm-1

The above table shows that there is one imaginary frequency that has wave number of -817.96 cm^-1. The relative vibrational mode is shown below,

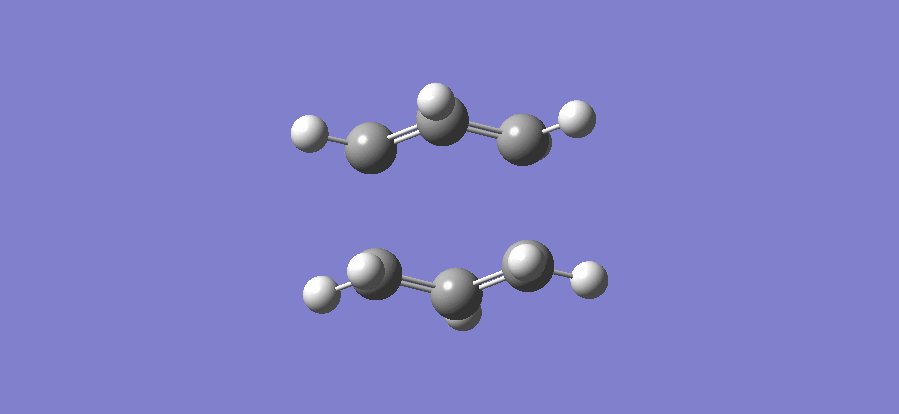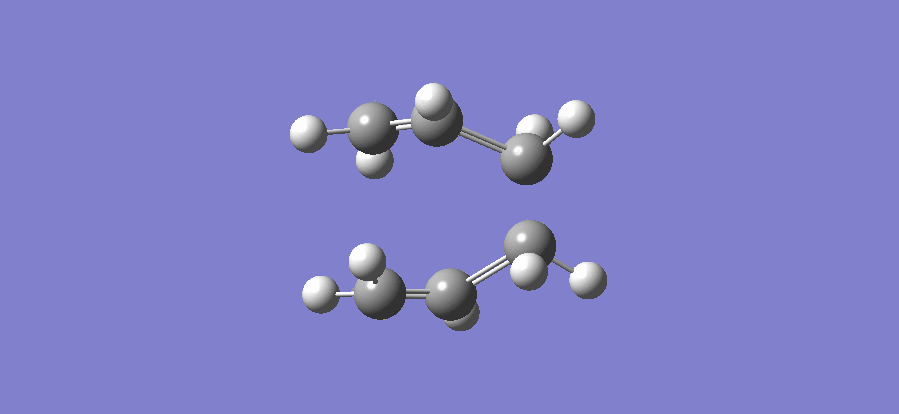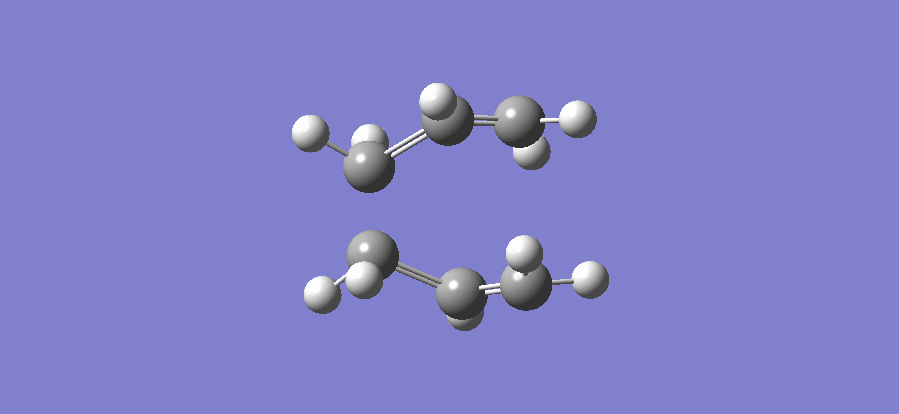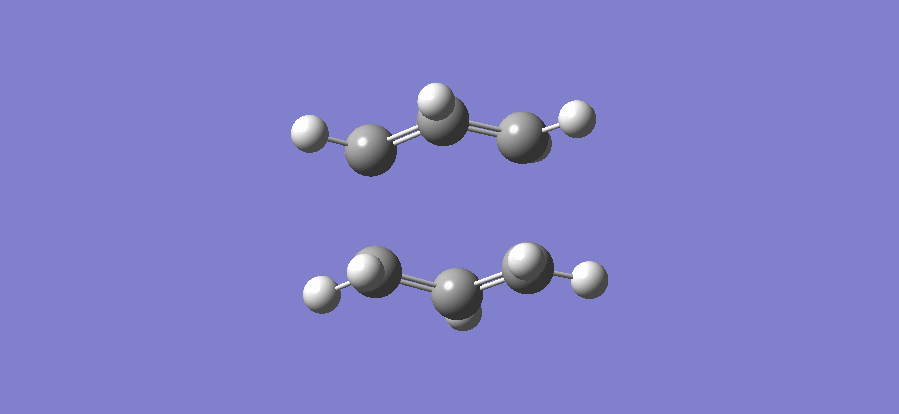
In this case, the two symmetrical terminal carbon atoms of each allyl fragments approach each other at the same time in order to form a bond while the other pair of terminal carbons move away from each other and facilitates a bond breaking. This conducts the mechanism of cope rearrangement reaction while a bond formation and a bond broken happen at the same time.

3.File Link

To access the .log file of optimization, click here. To view the screenshot of the vibration frequency table, click here. To view the screenshot of the calculated IR spectrum, click here.

b.Optimization at HF/3-21G level using Frozen Coordinates method

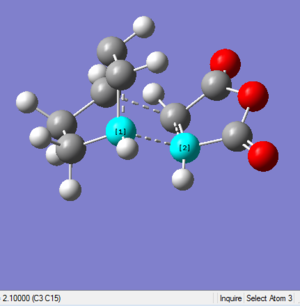
If there is not a reasonable guess structure for the transition structure, then the Berny approach may not work as the curvature of the surface may be significantly different at points far removed from the transition structure. Therefore, a better transition structure can generally be generated by freezing the reaction coordinate. In this case, both the bond breaking and bond making distances are set at a certain value(2.2 Å), otherwise, the parameters of atoms may lose after optimization to give the minimum energy structure.

1.Optimized structure of Chair Transition state

test molecule

2.General Information of Results

Gaussian Calculation Summary

Name of molecule	Chair Transition states structure
Job type	Optimization to a TS(Berny)
Basis Set	3-21G with Freeze Coordinate
Spin	Singlet
Total Energy	-231.61932232 a.u.
RMS Gradient Norm	0.00002205 a.u.
Current point group	C2h
Number of Imaginary Frequency	1
Magnitude of Imaginary frequency	-817.88 cm-1

3.Vibrational mode

4.File Link

To access the .log file of optimization, click here. To view the screenshot of the vibration frequency table, click here. To view the screenshot of the calculated IR spectrum, click here.

c.Optimization of Boat transition state at HF/3-21G level using QST2 method

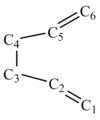
In this method, the Boat transition structure will be optimized by specifying the reactants and products for the Cope rearrangement reaction and interpolating the calculation between the two structures. As the reactant and product in this reaction are both 1,5-hexadiene, therefore numbering the atoms of both reactant and products in the same is very important(shown below).

First Attempt using QST2 method to optimize Boat transition structure

The reactant and product are labelled and placed like the way shown below.

However, the optimization failed. The chk file are shown below.

test molecule

This result looks a bit like the chair transition structure but more dissociated. The disadvantage of QST2 method is when the calculation linearly interpolated between the two structures, it simply translated the top allyl fragment and did not consider teh possibility of a rotation around the central bonds. Therefore, it is impossible to get the right boat transition structure if using these sets of reactant and product structures. Second approach has been made.

Second Attempt using QST2 method to optimize Boat transition structure

The structures of molecules before optimization are shown below:

Structure

Geometric Parameter       Bond Angle    
C1=C2-C3                  124.8113o         
C2-C3-C4                  100.0000o        
C2-C3-C4-C5               0o

1.Optimized structure of Boat Transition state

test molecule

2.General Information of Results

Gaussian Calculation Summary

Name of molecule	Boat Transition states structure
Job type	Optimization to a TS(QST2)
Basis Set	3-21G
Spin	Singlet
Total Energy	-231.60280198 a.u.
RMS Gradient Norm	0.00007270 a.u.
Current point group	C2v
Number of Imaginary Frequency	1
Magnitude of Imaginary frequency	-839.97 cm-1

3.Vibrational mode

Again, the vibrational mode of boat transition structure is similar to the chair transition structure above. The two nearby carbon atoms from each of the allyl fragments approach each other to make bond while the other pair of carbons are driving away resulting breaking of a bond.

4.File Link

To access the .log file of optimization, click here. To view the screenshot of the vibration frequency table, click here.

Nf710 (talk) 12:21, 11 February 2016 (UTC) Correct frequcies

d.IRC Analysis of both Boat and Chair transition structure

Even the transition structures have been found out, it is still difficult to predict that which conformer the trnasition structure will lead to. Therefore, IRC method allows it to follow the minimum energy path from the transition structure to the minimum point on a potential energy surface. It creates a series of points by taking small geometry steps in the direction where the gradient of slope of the energy surface is steepest. In this part, the number of points along the IRC was set as 50.

-IRC analysis of optimised Chair transition structure

1.General Information of Results

Gaussian Calculation Summary

Name of molecule	Chair Transition states structure
Job type	IRC
Basis Set	3-21G
Spin	Singlet
Total Energy	-231.62214783 a.u.
RMS Gradient Norm	0.00036454 a.u.
Current point group	C2h
Number of Imaginary Frequency	1
Magnitude of Imaginary frequency	-817.47 cm-1

2.File Link

To access the .log file of IRC calculation, click here. To view the screenshot of the vibration frequency table, click here.

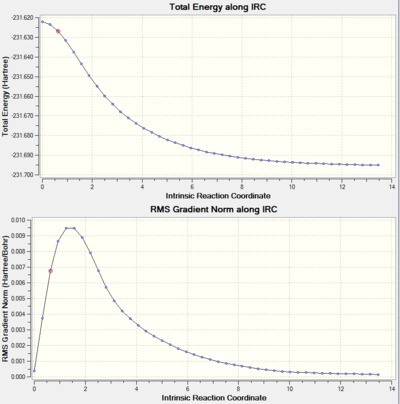
3.IRC Energy and RMS gradient graph

There are 44 intermediate geometries obtained, which are organized in order and show the geometric change following the calculated minimum energy path from the boat transition structure to either reactant or product. From the RMS gradient graph, it is clearly shown that the RMS gradient is approaching 0 that confirms this is an energy minimum. However, the first attempt of calculation of IRC has not reached a minimum geometry yet as the RMS gradient graph does not reach 0 which only shows a trend of approaching the minimum energy. Thus, further approach need to be made in order to reach the minimum energy conformation. There are different approaches can be made to reach the minimum point.

i.Take the last point on the IRC and run a normal minimization;

• Optimized structure of the last point of the IRC calculation

test molecule

• General Information of Results

Gaussian Calculation Summary

Name of molecule	Chair Transition states structure
Job type	Optimization to Minimum
Basis Set	3-21G
Spin	Singlet
Total Energy	-231.69166692 a.u.
RMS Gradient Norm	0.00003137 a.u.
Current point group	C2

• To access the .log file of IRC calculation, click here.

To view the screenshot of the vibration frequency table, click here. To view the vibration mode, click here.

ii.Restart the IRC and specify a larger number of points until it reaches a minimum;

• General Information of Results

Gaussian Calculation Summary

Name of molecule	Chair Transition states structure
Job type	IRC
Basis Set	3-21G
Spin	Singlet
Number of points	150
Energy of Last point	-231.69157883 a.u.
RMS Gradient Norm	0.00015225 a.u.
Current point group	C2

• IRC Energy and RMS gradient graph

-IRC analysis of optimised Boat transition structure

1.General Information of Results

Gaussian Calculation Summary

Name of molecule	Boat Transition states structure
Job type	IRC
Basis Set	3-21G
Spin	Singlet
Total Energy	-231.68298122 a.u.
RMS Gradient Norm	0.00010260 a.u.
Number of points	150
Current point group	Cs
Number of Imaginary Frequency	1

2.File Link

To access the .log file of IRC calculation, click here. To view the screenshot of the vibration frequency table, click here.

3.IRC Energy and RMS gradient graph

There are 45 intermediate geometries obtained, which are organized in order and show the geometric change following the calculated minimum energy path from the boat transition structure to either reactant or product. From the RMS gradient graph, it is shown that the RMS gradient at the final point is 0.000102599, but still not 0.Thus, it is still not reaching the minimum point on the potential surface.Further approach, for example increasing the no number of point to 200, need to be made in order to reach the minimum energy conformation.

Reoptimization of the chair and boat transition structures

Nf710 (talk) 12:24, 11 February 2016 (UTC) You ahvent said that it is explicitly gauche 2 but i will give you the credit as you have given it in a jmol.

-Reoptimization of the chair transition structures

1.Reoptimized structure

test molecule

2.General Information of Results

Gaussian Calculation Summary

Type of Transition Structure	Chair
Job type	Optimization to a TS(Berny)
Basis Set	6-31+G(D)
Spin	Singlet
Total Energy	-234.55696300 a.u.
RMS Gradient Norm	0.00001521 a.u.
Current point group	C2h

3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000026     0.000450     YES
RMS Force                0.000006     0.000300     YES
Maximum Displacement     0.000077     0.001800     YES
RMS Displacement         0.000026     0.001200     YES
Predicted change in Energy = -4.286567D-09
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

4.Frequency Calculations

Frequency calculations were carried out at the same level of theory(B3LYP/6-31G(D)). The frequency calculations show that there is one imaginary frequency at -567.78 cm^-1 which is lower than that of the HF/3-21G optimized structure at -817.96 cm^-1. The vibrational mode at -567.78 cm^-1 is shown below:

5.File Link

To access the .log file of optimization, click here. To view the screenshot of the vibration frequency table, click here.

-Reoptimization of the Boat transition structures

1.Reoptimized structure

test molecule

2.General Information of Results

Gaussian Calculation Summary

Type of Transition Structure	Boat
Job type	Optimization to a TS(Berny)
Basis Set	6-31+G(D)
Spin	Singlet
Total Energy	-234.54309306 a.u.
RMS Gradient Norm	0.00001081 a.u.
Current point group	C2v

3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000021     0.000450     YES
RMS Force                0.000005     0.000300     YES
Maximum Displacement     0.000596     0.001800     YES
RMS Displacement         0.000110     0.001200     YES
Predicted change in Energy = -4.704804D-09
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

4.Frequency Calculations

Frequency calculations were carried out at the same level of theory(B3LYP/6-31G(D)). The frequency calculations show that there is one imaginary frequency at -530.30 cm^-1 which is lower than that of the HF/3-21G optimized structure at -839.97 cm^-1. The vibrational mode at -530.30 cm^-1 is shown below:

5.File Link

To access the .log file of optimization, click here. To view the screenshot of the vibration frequency table, click here.

Results and discussion

1.Geometry Analysis

The structures of Chair transition structure after optimization at different levels and corresponding bond lengths with bond angles are shown below:

	HF/3-21G	B3LYP/6-31G(d)
Structure	test molecule	test molecule

Geometric Parameter           HF/3-21G          B3LYP/6-31G(D)    
C1-C2 Bond Length/Å            1.98059           2.0264     
C2-C3 Bond Length/Å            1.38925           1.40877     
C3-C4 Bond Length/Å            1.38925           1.40877     
C1=C2-C3 Bond Angle            101.84377o        103.28147o     
C2-C3-C4 Bond Angle            120.50908o        120.22418o
C2-C3-C4-C5 Dihedral Angle     68.47047o         65.76566o

The structures of Boat transition structure after optimization at different levels and corresponding bond lengths with bond angles are shown below:

	HF/3-21G	B3LYP/6-31G(d)
Structure	test molecule	test molecule

Geometric Parameter           HF/3-21G          B3LYP/6-31G(D)    
C1-C2 Bond Length/Å            1.38148           1.39416     
C2-C3 Bond Length/Å            2.13993           2.24121     
C3-C4 Bond Length/Å            1.38148           1.39416     
C1=C2-C3 Bond Angle            103.38282o        102.86558o     
C3-C4-C5 Bond Angle            121.66766o        122.59687o
C2-C3-C4-C5 Dihedral Angle     64.78779o         65.33357o

The overall change of geometry is relatively small. The large energy difference between those two calculations might be resulted from the change of dihedral angle of C₂-C₃-C₄-C₅. At B3LYP/31G(D)level, the C=C double bond overlap better with nearby carbon-carbon or carbon-hydrogen bond. This leads stronger σ-π conjugation and large stabilization energy. In general, the B3LYP/6-31G(D) method is more accurate than the HF/3-21G method as the optimized angles and bong lengths are closer to the real experimental values.. Nf710 (talk) 12:27, 11 February 2016 (UTC) Well done for using refernces here. But the lower basis is still pretty good at predicting what the bond lengths are, but it is just bad at predicting energies.

2.Thermochemistry

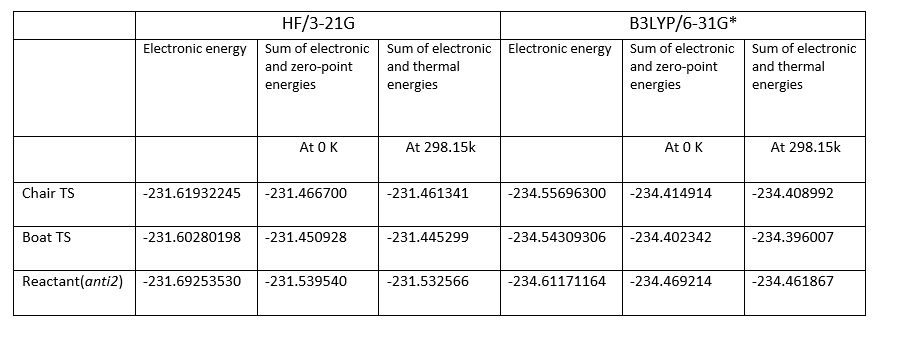
Summary of energies(in hartree)

• 1 hartree = 627.509 kcal/mol

Most of the data gives good alignment with the result shown on the script. And the energy between optimization using HF/3-21G method and B3LYP/6-31G(D) method is huge.(~3 a.u.where 1 a.u.=627.509 kcal/mol.

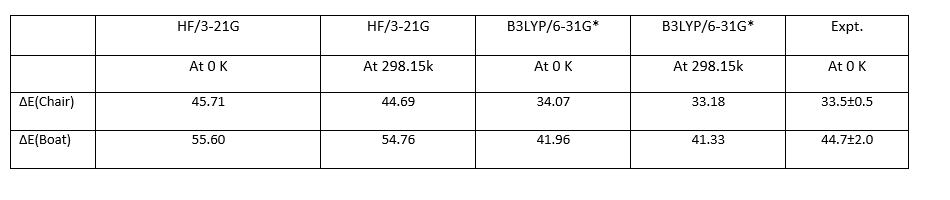
Summary of activation energies (in kcal/mol)

According to the Table of summery of activation energies, it is shown that the B3LYP/6-31G(D) method gives the values that are closer to the experimental values. For Chair transition states at 0 K, the B3LYP/6-31G(D) method gives an accuracy about 2.0%. And for Boat Transition states at 0 K, the B3LYP/6-31G(D) method gives an accuracy about 4.50%. Therefore, the higher level method B3LYP/6-31G(D) is more accurate comparing with the HF/3-21G method. This indicates the B3LYP/6-31G(D) basis set gives more stable structure as the total energy at B3LYP/6-31G(D) level is lower than at HF/3-21G level.

Nf710 (talk) 12:28, 11 February 2016 (UTC) Your energies are correct. In general this is a good report as you have done everything that has been asked of you. However you could have gone into alot more detail about the computational methods used. it seems like you dont have very much understanding there.

Example B: The Diels-Alder Cycloaddition

Cycloaddition is another type of pericyclic reactions. It permits carbon-carbon bond formation between two or more unsaturated molecules. Specifically, Diels-Alder reaction is a [4+2] cycloaddition between a conjugated diene and a substituted alkene to form a substituted cyclohexene system. It is considered the reaction occurs via a single, cyclic transition state , with no intermediates generated during the course of the reaction. In this experiment, the transition structures on potential energy surfaces in Diels-Alder reactions will be characterized using quantum mechanic approaches. Unlike from the Cope Rearrangement reaction, the Hartree-Fock and DFT methods have been used and developed. In this example, the AM1 semi-empirical molecular orbital method is used for calculations and analyses.

Diels-Alder Reaction Between Ethylene and Cis-Butadiene

The reaction scheme of Diels-Alder Reaction between cis-butandiene and ethylene is shown below:

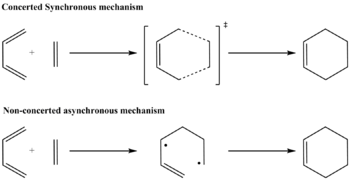
The approximation of mechanism for Diels-Alder reaction between ethylene and cis-Butadiene can be divided to two classes. 1.Concerted mechanisms: the two new carbon-carbon bonds are formed simultaneously. In the transition state, the two new forming bonds have the same lengths. 2.Non-concerted mechanisms: the transition state is a di-radical. One bond being formed while the other is not. In order to have an idea of the mechanism, the transition state needs to be approached and analyzed.

Optimizing the Reactants

1.Optimization of Cis-butadiene

1.1.Optimized structure of Cis-butadiene

test molecule

1.2.General Information of Results

Gaussian Calculation Summary

Name of Molecule	Cis-butadiene
Job type	Optimization to a minimum
Basis Set	Semi-empirical MO/AM1
Spin	Singlet
Total Energy	0.04879719 a.u.
RMS Gradient Norm	0.00001745 a.u.
Current point group	C2v

1.3.File Link

To access the .log file of optimization, click here.

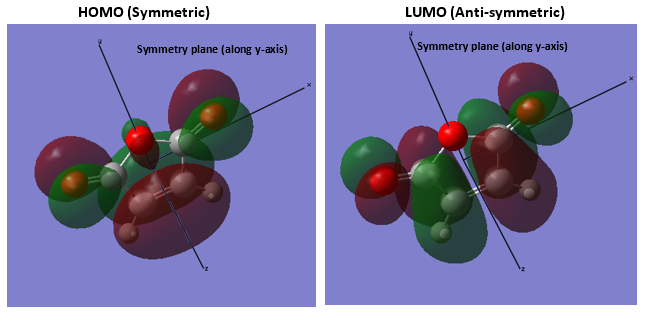
1.4.HOMO and LUMO Visualization (with symmetry plane)

.

2.Optimization of Ethylene

2.1.Optimized structure of Ethylene

test molecule

2.2.General Information of Results

Gaussian Calculation Summary

Name of Molecule	Ethylene
Job type	Optimization to a minimum
Basis Set	Semi-empirical MO/AM1
Spin	Singlet
Total Energy	0.02619029 a.u.
RMS Gradient Norm	0.00008755 a.u.
Current point group	D2h

2.3.File Link

To access the .log file of optimization, click here.

2.4.HOMO and LUMO Visualization(with symmetry plane)

.

Optimization of Transition structure

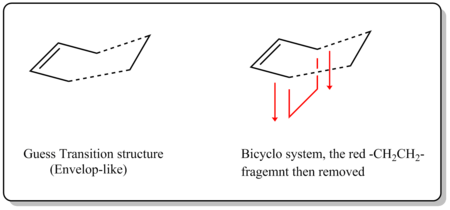
The transition structure has an envelop-like shape. In order to obtain the starting geometry, building a bicyclo system (shown below) and removing the -CH₂-CH₂- fragment later is a good way to begin with. The guess interfragment distance was set as 2.2 Å before optimization.

1.Optimization of Transition structure using Semi-Empirical MO/AM1 Method

1.1.Optimized structure of Transition state

test molecule

1.2.General Information of Results

Gaussian Calculation Summary

Name of Molecule	Transition state
Job type	Optimization to a TS(Berny)
Basis Set	Semi-empirical MO/AM1
Spin	Singlet
Total Energy	0.11165467 a.u.
RMS Gradient Norm	0.00001966 a.u.
Current point group	Cs

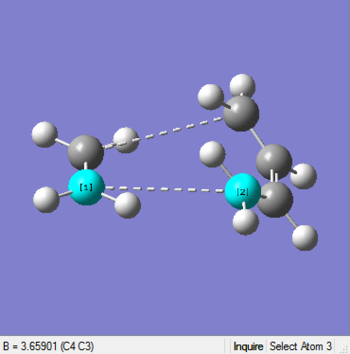
The structures of molecules before and after optimization with interfragment bond lengths(dash lines) are shown below:

Summery of structures and bond lengths before and after optimization

Before Optimization	After Optimization
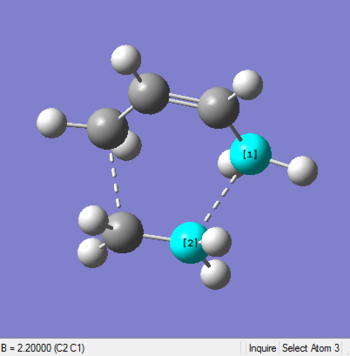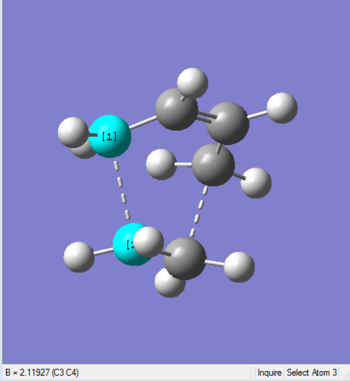
Bond Length 2.2 Å	Bond Length 2.11927 Å

1.3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000092     0.000450     YES
RMS Force                0.000011     0.000300     YES
Maximum Displacement     0.001382     0.001800     YES
RMS Displacement         0.000386     0.001200     YES
Predicted change in Energy = -2.328586D-08
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

1.4.Frequency Calculations

One imaginary frequency has been found at -956.35 cm^-1, indicating the existence of transition state. The vibrational mode at -956.35 cm^-1 is shown below:

1.5.File Link

To access the .log file of optimization, click here. To view the screenshot of the vibration frequency table, click here.

1.6.HOMO and LUMO Visualization(with symmetry plane)

.

2. IRC Calculation of Transition structure using Semi-Empirical MO/AM1 Method

In this case, the reaction coordinate is not symmetrical. Reaction coordinate needs to be computed in both directions. So both forward and and reverse will be done. And then number of point were set to 150 in order to reach the minimum energy geometry.

2.1.The Structure of the last point on the IRC

test molecule

2.2.General Information of Results

Gaussian Calculation Summary

Name of Molecule	Transition state structure
Job type	IRC Calculation(both directions)
Basis Set	Semi-empirical MO/AM1
Spin	Singlet
Total Energy	0.07462766 a.u.
RMS Gradient Norm	0.00004555 a.u.
Current point group	Cs

The structures of molecules before and after calculation with interfragment bond lengths(dash lines) are shown below:

Summery of structures and bond lengths before and after Calculation

Before Optimization	After Optimization	After Optimization(Last point)
Bond Length 2.2 Å	Bond Length 3.65901 Å	Bond Length 1.157879 Å

2.3.IRC Energy and RMS gradient graph

As the RMS gradient graph is shown above, the gradient reaches O in the end, which indicates the energy minimum has reached. Therefore, no further approach is required.

2.4.File Link

To access the .log file of IRC Calculation, click here.

3.Reoptimization of Transition structure using 6-31G(D) Basis Method

Reoptimization using more accurate method and higher level at B3LYP/6-31G(D) has been computed in order to make comparison between different methods. The initial structure used is the same as the one used before. And the interfragment distance is still set as 2.2 Å.

3.1.Optimized structure of Transition state

test molecule

3.2.General Information of Results

Gaussian Calculation Summary

Name of Molecule	Transition state
Job type	Optimization to a TS(Berny)
Basis Set	6-31G(D)
Spin	Singlet
Total Energy	-234.54389652 a.u.
RMS Gradient Norm	0.00001675 a.u.
Current point group	Cs

The structures of molecules before and after optimization with interfragment bond lengths(dash lines) are shown below:

Summery of structures and bond lengths before and after optimization

Before Optimization	After Optimization
Bond Length 2.2 Å	Bond Length 2.27244 Å

3.3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000034     0.000450     YES
RMS Force                0.000010     0.000300     YES
Maximum Displacement     0.000957     0.001800     YES
RMS Displacement         0.000266     0.001200     YES
Predicted change in Energy = -3.817143D-08
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

3.4.Frequency Calculations

One imaginary frequency has been found at -524.81 cm^-1, indicating the existence of transition state. The vibrational mode at -524.81 cm^-1 is shown below:

3.5.File Link

To access the .log file of optimization, click here. To view the screenshot of the vibration frequency table, click here.

3.6.HOMO and LUMO Visualization(with symmetry plane)

.

Comparing the HOMO and LUMO diagram with previous session using AM1 semi-empirical MO basis set, they are exactly the same. This confirm a transition structure for the Diels Alder reaction has successfully obtained.

Results and discussion

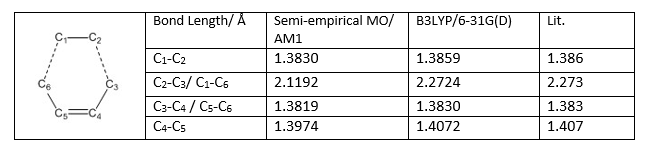
1.Geometry Analysis

The bond lengths between different carbons after optimization using Semi-empirical MO/ AM1 and B3LYP/6-31G(D) two different basis sets are shown below:

The literature values can be found here. It is shown from the table above that the B3LYP/6-31G(D) method is more accurate than Semi-empirical MO/ AM1 Method as those values are almost perfectly match with the experimental data from the literature.

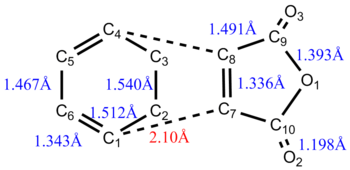
Illustration of geometry for transition states in more details including the reactants are shown below;

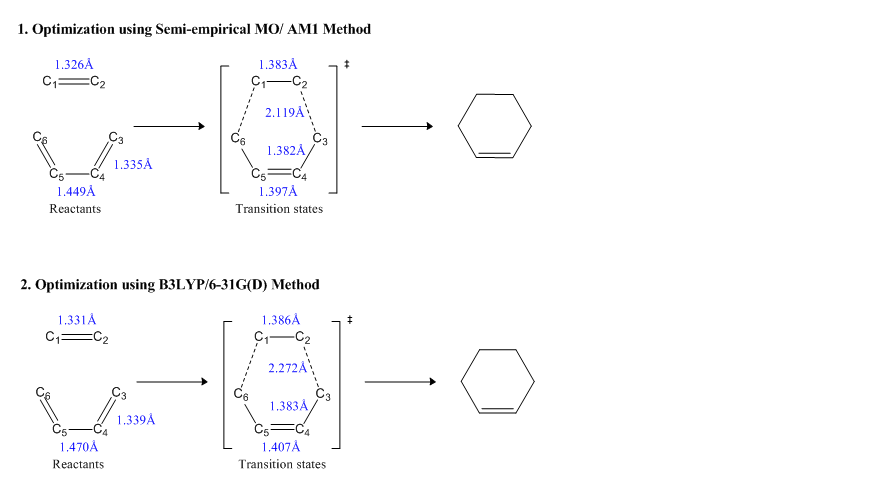
The literature values of reactants bond lengths also can be found here. In order to make a comparison between different types carbon-carbon bonds, some typical carbon-carbon bond lengths are shown below,

C-C bond lengths(pm)

sp3 - sp3	154
sp3 - sp2	150
sp2 - sp2	147

The Van der waals radius is defined as half of the internuclear separation of two non-bonded atoms of the same element on their closest possible approach. The Van der waals raius of carbon can be checked here, which is 170 pm. In theory and according to the literature values above, the bond length of C(sp³) - C(sp²)should be between C(sp³) - C(sp³) bond and C(sp²) - C(sp²)bond. As the reaction will form two new σ C-C bonds that is (sp³)-(sp³) character, the interfragment distance need to be computed as larger than the bond length of C4-C5 in cis-butadiene, which has(sp³)-(sp²)character. However, on the other hand, the interfragment distance need to be as small as possible so that the structure will look as close as the transition structure. Therefore, in this experiment, the interfragment distance was set as 2.2Å. In the literature, the bond length of C₁=C₂ in the product is 1.337Å while the bond length of C₂-C₃ is 1.510Å and C₃=C₄ is 1.537Å. This proves the theory where C(sp³) - C(sp²) bond length lies between C(sp³) - C(sp³) bond and C(sp²) - C(sp²)bond. In the transition state, the C(sp²)= C(sp²) bond is generally loesen and longer than typical value and C(sp³) - C(sp³) bond is slightly shorter than typical value as new σ C-C bonds are forming. This gives indication that they are neither C=C double bond nor C-C single bond, but a state between those two bonds.

2.Reaction Mechanisms It was mentioned at the beginning of this experiment, there are two possible classes of Mechanisms for Diels-Alder Reaction, synchronous/concerted or asynchronous/nonconcerted(Mechanisms are shown below).

For reaction between Cis-butadiene and ethylene, the formation of the two bonds is synchronous according to the animation of the transition state comparing with the vibration mode of lowest positive frequency(shown below)while the interfragment distance does not change when vibrating.

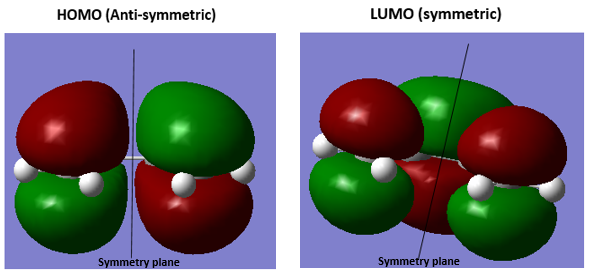
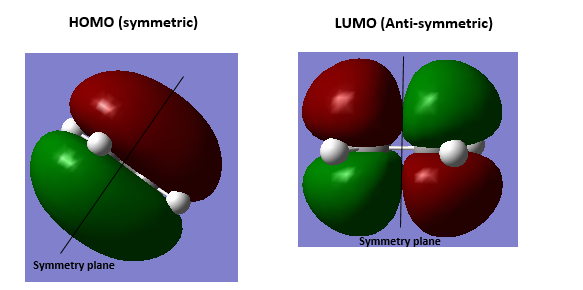
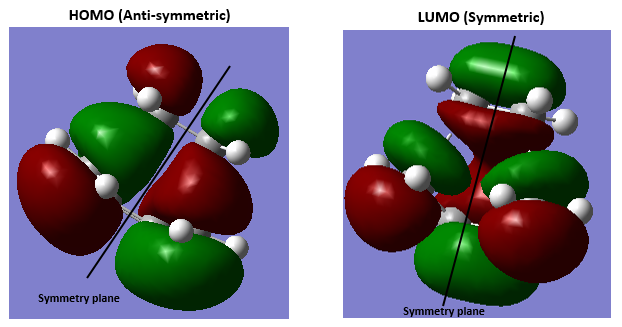
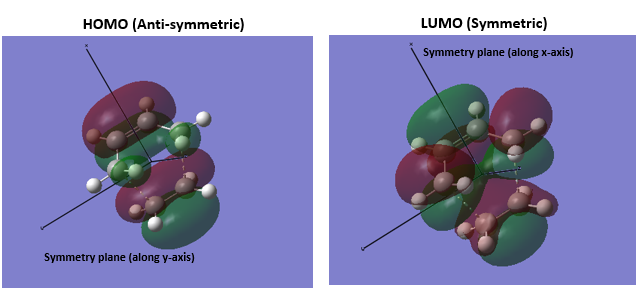
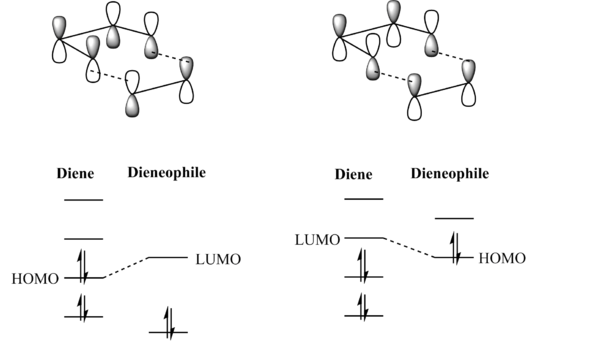
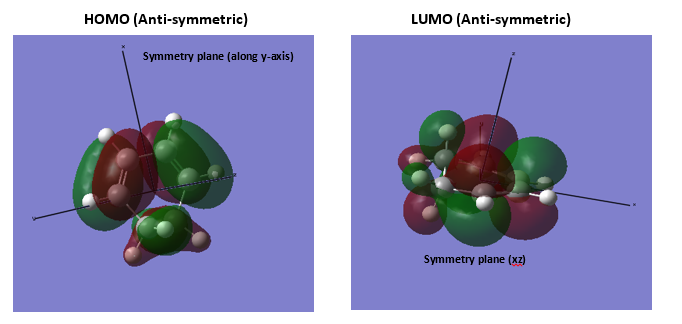
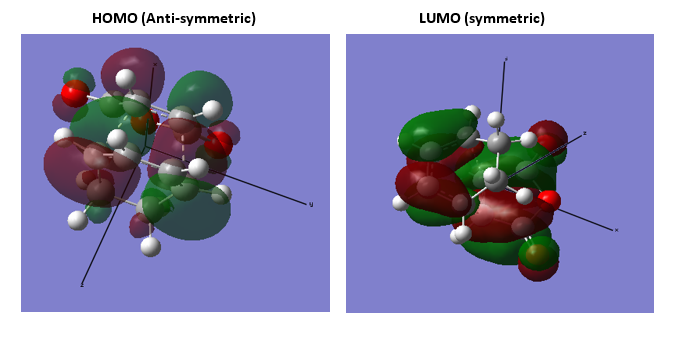
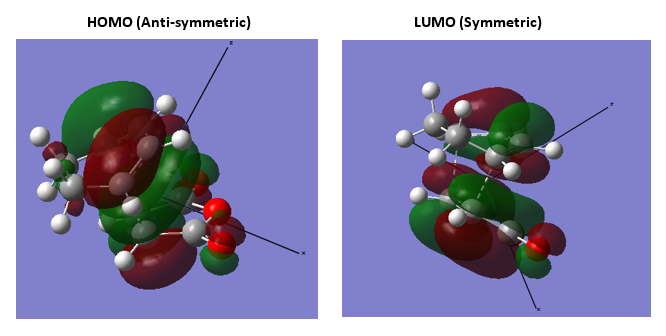
3.Molecular Orbitals The plotted HOMO and LUMO for both ethylene and butadiene are shown above, the HOMO of ethylene and the LUMO of butadiene are both symmetric with respect to the reflection plane. The LUMO of ethylene and the HOMO of butadiene are both asymmetric with respect to the reflection plane. Thus in this reaction, the HOMO-LUMO pairs of orbital that interact, and energetically, the HOMO of the resulting adduct with two new σ bonds is asymmetric as the image shown below.

It is clearly shown that at the transition state structure, the HOMO is anti-symmetric which shows a weak bonding character formed by interaction between LUMO of ethylene and HOMO of butadiene.And the LUMO at the transition state is symmetric with anti-bonding character and formed by interaction between HOMO of ethylene and LUMO of butadiene. The interaction between two reactants orbitals are shown below.

For a Diels-alder reaction, in theory, there are two possible interaction of orbitals in transition states. HOMO can be either asymmetrical or symmetrical. The HOMO of ethylene and LUMO of butadiene can interact resulting adduct is symmetric while the LUMO of ethylene and HOMO of butadiene can also interact forming an asymmetric adduct. However, in this experiment, butadiene’s Ψ2(the HOMO) is more electron sufficient than the ethylene, while the electron-deficient ethylene's π* is the LUMO,which can be filled more efficiently, resulting a good stabilization of the product and allowed the reaction happens.

However, the HOMO-LUMO energy gap can be reversed by switching the substitution pattern(Orbital diagram is shown above): i.e. the diene’s Ψ3 might be considered the LUMO if an electron withdrawing group is attached and makes it sufficiently electron-deficient while an electron donating group is attached to the alkene and raises the dienophile’s filled π orbital’s energy sufficiently in order to make it the HOMO which is not the case in this experiment.

Diels-Alder Reaction Between Cyclohexa-1,3-diene and Maleic anhydride

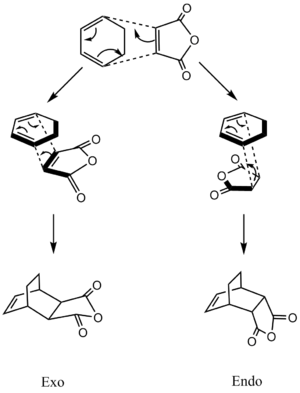
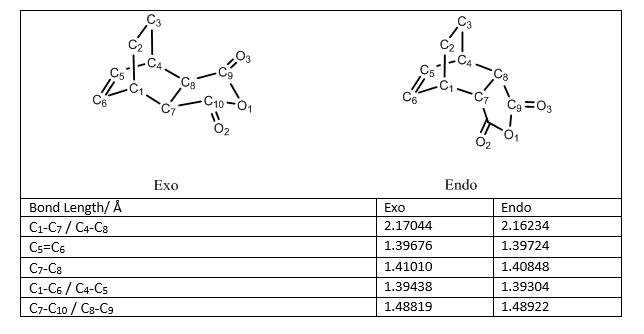
When both the diene and the dienophile are suitably substituted, a stereochemical feature arises because the reactants may approach each other in two distinct orientations. The substituent on the dienophile may be directed away from the diene (exo approach) or toward the diene (endo approach). This stereochemical difference is often found with cyclic compounds.One of the example is the reaction between Cyclohexa-1,3-diene and Maleic anhydride. The reaction scheme is shown below,

In most Diels-Alder reactions, when the product distribution is under kinetic control, the endo adduct is preferentially while the exo adduct is thermodynamically preferred.

Optimizing the Reactants

1.Optimization of Maleic Anhydride

1.1.Optimized structure of Maleic Anhydride

test molecule

1.2.General Information of Results

Gaussian Calculation Summary

Name of Molecule	Maleic Anhydride
Job type	Optimization to a minimum
Basis Set	B3LYP/6-31G(D)
Spin	Singlet
Total Energy	-379.28953493 a.u.
RMS Gradient Norm	0.00011922 a.u.
Current point group	C2v

1.3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000276     0.000450     YES
RMS Force                0.000086     0.000300     YES
Maximum Displacement     0.001323     0.001800     YES
RMS Displacement         0.000455     0.001200     YES
Predicted change in Energy = -5.604720D-07
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

1.4.File Link

To access the .log file of optimization, click here.

1.5.HOMO and LUMO Visualization (with symmetry plane)

.

2.Optimization of Cyclohexa-1,3-diene

2.1.Optimized structure of Cyclohexa-1,3-diene

test molecule

(It looks like you might have taken the wrong geometry for the mol file Tam10 (talk) 11:43, 11 February 2016 (UTC))

2.2.General Information of Results

Gaussian Calculation Summary

Name of Molecule	Cyclohexa-1,3-diene
Job type	Optimization to a minimum
Basis Set	RB3LYP/6-31G(D)
Spin	Singlet
Total Energy	-233.41891186 a.u.
RMS Gradient Norm	0.00001598 a.u.
Current point group	C2v

2.3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000041     0.000450     YES
RMS Force                0.000008     0.000300     YES
Maximum Displacement     0.000551     0.001800     YES
RMS Displacement         0.000166     0.001200     YES
Predicted change in Energy = -2.021209D-08
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

2.4.File Link

To access the .log file of optimization, click here.

2.5.HOMO and LUMO Visualization (with symmetry plane)

.

Optimization of Exo and Endo Transition Structures

1.Optimization of Exo adduct

The guess Exo transition structure was shown above by combining the optimiszed cyclohexa-1,3-diene and maleic anhydride structures with two partially formed C-C bonds of 2.1 Å bond length while the optimised structure is shown below, which has bond length of 2.17044 Å.

1.1.Optimized structure of Exo adduct

test molecule

1.2.General Information of Results

Gaussian Calculation Summary

Name of Molecule	Exo adduct
Job type	Optimization to a TS(Berny)
Basis Set	AM1 semi-empirical MO
Spin	Singlet
Total Energy	-0.05041985 a.u.
RMS Gradient Norm	0.00000551 a.u.
Current point group	Cs

1.3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000013     0.000450     YES
RMS Force                0.000002     0.000300     YES
Maximum Displacement     0.000658     0.001800     YES
RMS Displacement         0.000130     0.001200     YES
Predicted change in Energy = -2.783760D-09
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

1.4.Frequency Calculations

There are 63 frequencies are included. One imaginary frequency has been found at -812.09 cm^-1, indicating the existence of transition state. The vibrational modes at -812.09 cm^-1 and smallest positive frequency are both shown below:

1.5.HOMO and LUMO Visualization (with symmetry plane)

.

1.6.File Link

To access the .log file of optimization, click here. To view the screenshot of the vibration frequency table, click here.

2.Optimization of Endo adduct

The guess Endo transition structure was shown above with two partially formed C-C bonds of 2.1 Å bond length while the optimised structure is shown below, which has bond length of 2.16234 Å.

2.1.Optimized structure of Endo adduct

test molecule

2.2.General Information of Results

Gaussian Calculation Summary

Name of Molecule	Endo adduct
Job type	Optimization to a TS(Berny)
Basis Set	AM1 semi-empirical MO
Spin	Singlet
Total Energy	-0.05150480 a.u.
RMS Gradient Norm	0.00000579 a.u.
Current point group	Cs

2.3.Real output

Item                     Value        Threshold    Converged?
Maximum Force            0.000011     0.000450     YES
RMS Force                0.000003     0.000300     YES
Maximum Displacement     0.001503     0.001800     YES
RMS Displacement         0.000291     0.001200     YES
Predicted change in Energy = -7.023995D-09
Optimization completed.
-- Stationary point found.

Both forces and displacements are converged. This shows that the optimization is completed and the resultant molecules is at its minimum energy status.

2.4.Frequency Calculations

There are 63 frequencies are included. One imaginary frequency has been found at -806.35 cm^-1, indicating the existence of transition state. The vibrational modes at -806.35 cm^-1 and smallest positive frequency are both shown below:

2.5.HOMO and LUMO Visualization (with symmetry plane)

.

2.6.File Link

To access the .log file of optimization, click here. To view the screenshot of the vibration frequency table, click here.

Results and discussion

1.Geometry Analysis

The bond lengths between different carbons after optimization using Semi-empirical MO/ AM1 basis set for both Exo and Endo adducts are shown below:

The overall geometries of each fragment (Cyclohexa-1,3-diene and Maleic anhydride) do not change a lot from Exo transition structure to Endo transition sturcture as the bond lengths and bond angles did not change a lot before and after. And comparing the bond lengths of pure carbon-carbon bonds(list in previous session), it proves that it has the character between pure double bond and pure single bond character. In this experiment, the partial bonds that has neither pure double bond character or pure single bond character occurs in the transition state. The guess interfragmental distance, which is 2.1 Å, is quite close to calculated transition structure. For comparison,illustration of geometry of both reactants, cyclohexa-1,3-diene and Maleic anhydride, are shown below;

(What about steric effects from the side group of maleic anhydride? Tam10 (talk) 11:43, 11 February 2016 (UTC))

• As the AM1 semi-empirical MO method is not as accurate as the B3LYP/6-31G(D) method, therefore, the computed bond lengths are not compared with literature. Further calculation and approach can be made if time allowed.

2.Reaction Mechanisms and Molecular Orbitals

The total energy of exo adduct and endo adduct are -0.05041985a.u. and -0.05150480a.u. respectively. Therefore the relative energy is equal to 0.68082kcal/mol (or 0.00108495a.u.). Comparing the energy difference between HOMO and LUMO, the relative energy between endo and exo adducts are negligible. This indicates the reaction can occur both way as the energy barrier needs to overcome is relatively small. This matches the assumption at the beginning of this session, this is an Endo-Exo selective reaction as both the diene and the dienophile are suitably substituted resulting arising of stereochemical feature. Generally in Diels-Alder reactions, the endo adduct is preferentially when the product distribution is under kinetic control. There are some hypotheses used to explain this selectivity :

1. Alder proposed that endo addition was the consequence of a plane-to-plane orientation of diene and dienophile with "maximum accumulation of double bonds". Since this same orientation would promote stability in a molecular complex, complex formation between the reactants may be the main effect of preference of endo addition occurred.

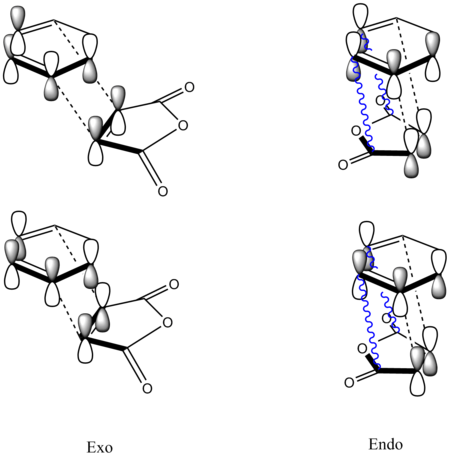
2. Woodward and Hoffmann ascribe endo addition to interaction of occupied orbitals with unoccupied orbitals between the diene and the dienophile, the endo transition state conformation being favored by orbital symmetry relative to the exo conformation. Using the model of frontier orbitals, the interactions between HOMOs with LUMOs are shown below. The main interactions that will form the bonds are shown by plain bold lines, the secondary interactions(Secondary orbital overlap effect), responsible for the endo-exo selectivity, are shown by blue squiggly lines. If the molecules approach so closely that the secondary interactions can be the dominant effect of the selectivity of the reaction. More specifically, the secondary orbital overlap effect in this reaction indicates the attaching electron withdrawing C=O group at Maleic Anhydride. The pi orbitals on C=O groups interact with HOMO of diene, which stabilize the endo form.

(Your pi orbitals are on the wrong atoms in cyclohexadiene Tam10 (talk) 11:43, 11 February 2016 (UTC))

3.The transition states can also give an explanation of this selectivity which is the purpose of this experiment. The transition state in an asynchronous mechanism can be described using several resonance structures(Radical and zwitterion structure are shown below). The reason why the endo adduct is favoured is the proximity of the two charges stabilizes this structure at transition state(zwiterrion).

For the reaction between Cyclohexa-1,3-diene and Maleic anhydride, the forming bond lengths are 2.17044 Å in the exo transition state and 2.16234 Å in the endo transition state. These results confirms that the mechanism for this reaction is asynchronous. Moreover, endo transition state is more assymetric as the zwitterion resonance strucure is more favoured than in the exo adduct forming reaction.

(Is this the right image? This looks like the dimerisation of cyclopentadiene Tam10 (talk) 11:43, 11 February 2016 (UTC))

Further Discussion

There are several factors that have been neglected in this experiment during calculation may influence on the transition states. For example,

1.Influence of the temperature

Due to time limitation, these calculations cannot be carried out. Therefore, in theory, the yield of the Diels-Alder reaction decreases with the temperature, which means the reaction equilibrium will shift to the thermodynamic product. As Diels-Alder reactions are reversible, normally, with a relatively large temperature, reverse reaction will be favoured. This is due to the negative entropy that favours dissociation, and its importance increases with temperature. However, for some reactions, e.g.Diels-Alder reaction of two cyclopentadiene, there is no change in the endo-exo selectivity, and that the entropy differences between endo and exo products and transition states are so small that there is no need to take them into account.

2.Influence of catalyst

The use of catalyst is to reduce the activation energy barrier of reaction resulting an increasing of reaction rate. There are some certain catalysts that will only lower the activation energy of one of the transition state. Therefore, the yield of the of both products(exo-endo ratio)will change,too.

3.Influence of the entropy(Negligible)

The reaction entropy and activation entropy differences are very small. Thus, their effect can be neglected on the Gibbs Free-Energies(G°_r and G_‡ ) (calculated using equation G_‡ = H_‡ - TS_‡ and K = e^{- G°_r/RT} = e^{-(H°_r -TS°_r )/RT)}. Because the exo and the endo reactions are very similar. In both cases, we have the addition of two reagents that yield one product, and the bond transformations are identical. In order to compare Diels-Alder reactions, studying of reaction enthalpies will be a better approximation.(Use Hess' law can calculate it easily with the outputs of the calculations which are often heats of formation). The reaction enthalpy differences are almost the same as those of Gibbs free energy.