Rep:Mod:Anjli
All the information on this wiki page was found using a software called Gaussview.
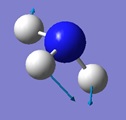
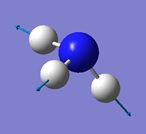
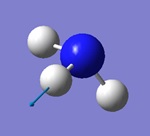
NH3 molecule
The first molecule analysed was ammonia, NH3.
Calculation summary of NH3
Calculation method is RB3LYP.
Basis set is 6-31G(d,p).
Final energy E(RB3LYP) = -56.55777 a.u.
RMS gradient = 0.00000485 a.u.
Point group of molecule is C3V.
Item table for NH3
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Jmol dynamic image of NH3
Ammonia molecule |
Bond length and angle information of NH3
Optimised N-H bond length = 1.02 Å (accurate to ≈ 0.01 Å)
Optimised H-N-H bond angle = 106° (accurate to ≈ 1°)
NH3 Optimisation file link
The NH3 optimisation file is linked to here
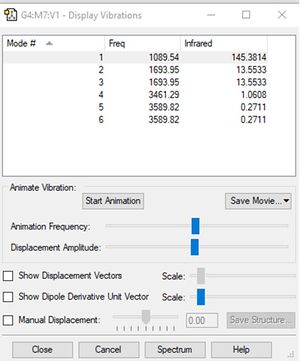
Vibrational analysis of NH3
Display vibrations table for NH3
Wavenumber and intensity of each vibration for NH3
| Wavenumber(cm-1) | 1090 | 1694 | 1694 | 3461 | 3590 | 3590 |
| Symmetry | A1 | E | E | A1 | E | E |
| Intensity (arbitrary units) | 145 | 14 | 14 | 1 | 0 | 0 |
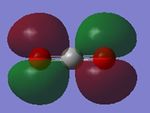
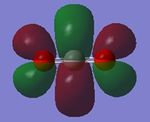
| Image |  |
 |
 |
 |
 |
|
The number of modes expected for NH3, according to the 3N-6 rule, is 6.
Vibrations with the wavenumber 1694cm-1 and 3590cm-1 are degenerate.
The "bending" vibrations are at wavenumbers, 1090cm-1 and 1694cm-1. The "stretching" vibrations are at wavenumbers, 3461cm-1 and 3590cm-1.
The vibration at wavenumber, 3461cm-1, is highly symmetric.
The vibration at wavenumber, 1090cm-1, is known as the umbrella mode.
I would expect to see 2 bands in an experimental spectrum of gas ammonia at wavenumbers, 1090cm-1 and 1694cm-1. Only one band would be seen at 1694cm-1 because of the degenerate vibrations. There is no change in dipole of the vibrations at wavenumbers, 3461cm-1 and 3590cm-1 so no band relating to this would be seen in the IR spectrum.
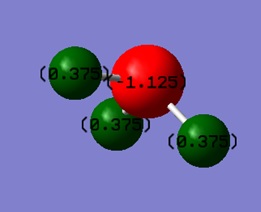
Atomic (NBO) charges of NH3
Charge on the N-atom is -1.125.
Charge on the H-atom is 0.375.
I had expected the charge of N to be negative and the charge of H to be positive. This is because N is more electronegative than H therefore it pulls the electrons, making up the N-H bond, to itself. This would cause it to have a negative charge.
N2 molecule
The second molecule analysed was nitrogen, N2.
Calculation summary of N2
The calculation method is RB3LYP
Basis set is 6-31G(d,p).
Final energy E(RB3LYP) = -109.52413 a.u.
RMS gradient = 0.00000060 a.u.
Point group of molecule is D*H.
Item table for N2
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Jmol dynamic image of N2 molecule
Nitrogen molecule |
Bond length of N2
Optimised N≡N bond length = 1.11 Å (accurate to ≈ 0.01 Å)
N2 Optimisation file link
The N2 optimisation file is linked to here
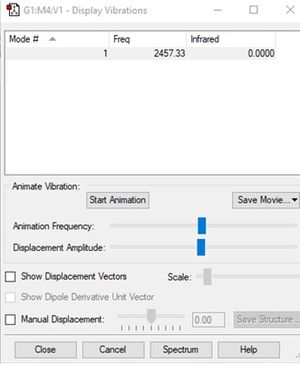
Vibrational analysis of N2
Display vibrations table for N2
Wavenumber and intensity of each vibration for N2
| Wavenumber(cm-1) | 2457 |
| Symmetry | SGG |
| Intensity (arbitrary units) | 0 |
| Image |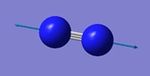 
|
The number of modes expected for N2, according to the 3N-5 rule, is 1.
There is only one vibration at wavenumber, 2457cm-1.
I would expect to see no bands in an experimental spectrum of nitrogen as there is no dipole on the molecule.
Atomic(NBO) charges of N2
Charge on both the N-atoms is 0.
I had expected the charges on each N atom to be 0, as N2 is a diatomic, so there is no dipole.
Structure from the CCDC that includes a coordinated N2
A CCDC refcode of a mono-metallic TM complex that coordinates N2 is DAYSUR
Link to structure is here: [1]
The mono-metallic TM complex, mer-Chloro-dinitrogen-(methylisocyanide)-tris(trimethylphosphite)-rhenium(i) is shown on the right.
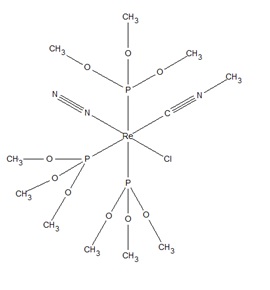
The bond distance of N-N in the crystallised structure is 1.03779 Å
The computational bond distance (bond distance I obtained) of N-N is 1.10550 Å
The transition metal N-N bond distance is shorter than the usual N-N bond length. This means the bond in the complex is stronger. The bond strength is determined by the even distribution of electron density between two atoms. Therefore when a transition metal is attached to an N, the N attracts the electron density from the metal complex. As a result, this strengthens and shortens the N-N bond on the complex compared to the bond of N2 alone. However, typically the N-N bond length in the TM complex should be longer as the rest of the molecule of the TM complex pulls the electron density, weakening the N-N bond. Computational error must also be accounted when measuring the bond lengths. This error may have caused the differences in the values and caused the N-N bond length in the TM complex to be shorter.
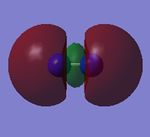
Molecular orbitals of N2 (Independence)
| MO type | MO 1 | MO 2 | MO 3 | MO 4 | MO 5 and 6 | MO 7 | MO 8 and 9 | MO 10 |
| Energy value of MO (a.u.) | -14.44676 | -14.44512 | -1.12383 | -0.55342 | -0.46240 | -0.42688 | -0.02412 | 0.41366 |
| MO structure |  |
 |
 |
 |
 |
 |
 |
|
| Explanation of MO | This MO is the lowest in energy (has the most negative energy value), as it is the first orbital to be occupied by electrons. | This MO is the next highest in energy, however it is still low in energy because it is still the core orbital. | MO 3 is larger than MO 1 therefore the bonding overlap is more extensive so only see one extended surface. It is also much higher in energy. This is because these electrons are occuying a new shell which is further from the nucleus. | The energy difference between MO 3 and MO 4 is much larger than the energy difference between MO 1 and MO 2. This is because they overlap better. | These MOs have the same energy values and therefore are degnerate. They are both occupied. They also have the same MO diagram structure to each other. These valence orbitals form the pi bond in chemical bonding. | This bonding, occupied MO consists of two types of interactions - sigma along the bond and pi perpendicular to the bond. This is called s-p mixing. | These MOs are antibonding and unoccupied. They also have the same energy value and so are degenerate. They have a higher energy than MO 7 as they are the antibonding orbitals and therefore more unstable. | MO 10 has the highest energy value and therefore is the most unstable MO. It is antibonding and unoccupied. It is most unstable antibonding MO because it has 3 nodes, which is the highest number of nodes, in this case. |
The higher energy MOs than MO 10 are not used because their shapes are not reliable.
H2 molecule
The third molecule analysed was hydrogen, H2.
Calculation summary of H2
Calculation method is RB3LYP.
Basis set is 6-31G(d,p).
Final energy E(RB3LYP) = -1.17854 a.u.
RMS gradient = 0.00000017 a.u.
Point group of molecule is D*H.
Item table for H2
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Jmol dynamic image of H2 molecule
Hydrogen molecule |
Bond length of H2
Optimised H-H bond length = 0.74 Å (accurate to ≈ 0.01 Å)
H2 Optimisation file link
The H2 optimisation file is linked to here
Vibrational analysis of H2
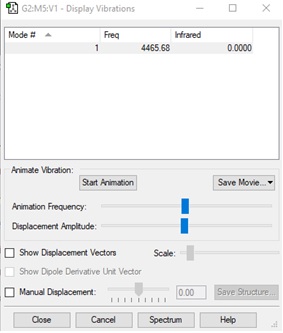
Display vibrations table for H2
Wavenumber and intensity of each vibration for H2
| Wavenumber(cm-1) | 4466 |
| Symmetry | SGG |
| Intensity (arbitrary units) | 0 |
| Image | 
|
The number of modes expected for H2, according to the 3N-5 rule, is 1.
There is only one vibration at wavenumber, 4466cm-1.
I would expect to see no bands in an experimental spectrum of hydrogen as there is no dipole on the molecule.
Atomic(NBO) charges of H2
Charge on both the H-atoms is 0.
I had expected the charges on each H atom to be 0, as H2 is a diatomic, so there is no dipole.
Haber-Bosch reaction energy calculation
E(NH3)= -56.55777 a.u.
2*E(NH3)= -113.11553 a.u.
E(N2)= -109.52413 a.u.
E(H2)= -1.17854 a.u.
3*E(H2)= -3.53562 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579 a.u.
ΔE in kJ/mol = -0.05579 x 2625.5 = -146.5 kJ/mol
The ammonia product is more stable than the gaseous reactants as the reaction is exothermic and therefore favourable. Also, the product has a lower energy than the reactants therefore it more stable.
CO2 molecule
I chose to analyse carbon dioxide, CO2.
Calculation summary of CO2
Calculation method is RB3LYP.
Basis set is 6-31G(d,p).
Final energy E(RB3LYP) = -188.58094 a.u.
RMS gradient = 0.00001154 a.u.
Point group of molecule is D*H
Item table for CO2
Item Value Threshold Converged? Maximum Force 0.000025 0.000450 YES RMS Force 0.000017 0.000300 YES Maximum Displacement 0.000022 0.001800 YES RMS Displacement 0.000015 0.001200 YES
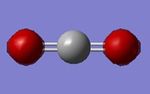
Jmol dynamic image of CO2 molecule
Carbon dioxide molecule |
Bond length and angle information of CO2
Optimised C=O bond length = 1.17 Å (accurate to ≈ 0.01 Å)
Optimised O=C=O bond angle = 180° (accurate to ≈ 1°)
CO2 Optimisation file link
The CO2 optimisation file is linked to here
Vibrational analysis of CO2
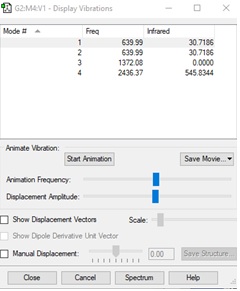
Display vibrations table for CO2
Wavenumber and intensity of each vibration for CO2
| Wavenumber(cm-1) | 640 | 640 | 1372 | 2436 |
| Symmetry | PTU | PTU | SGG | SGU |
| Intensity (arbitrary units) | 31 | 31 | 0 | 546 |
| Image |  |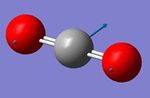
 |
 |
|
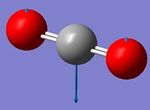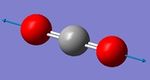The number of modes expected for NH3, according to the 3N-5 rule, is 4.
Vibrations with the wavenumber, 640cm-1 are degenerate.
The "bending" vibrations are both at wavenumber, 640cm-1. The "stretching" vibrations are at wavenumbers, 1372cm-1 and 2436cm-1.
The vibration at wavenumber, 1372cm-1, is highly symmetric.
I would expect to see 2 bands in an experimental spectrum of gas carbon dioxide, eventhough there are 4 vibrations. This is because of the degenerate vibrations at wavenumber, 640cm-1. The degenerate vibrations would show one band in the spectrum. Also, there is no change in dipole in the vibration at 1372cm-1 therefore, no band would be seen in the spectrum corresponding to it.
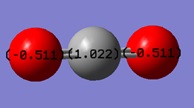
Atomic(NBO) charges of CO2
Charge on the C-atom is 1.022.
Charge on the O-atom is -0.511.
I would expect the charge of O to be negative and the charge of C to be positive. This is because O is more electronegative than C therefore it pulls the electrons, making up the C=O bond, to itself. This would cause it to have a negative charge.
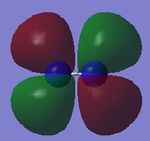
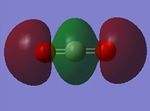
MOs of CO2 molecule
| MO type | MO 1 | MO 4 | MO 6 | MO 8 and 9 | MO 10 and 11 | MO 12 and 13 | |
| Energy value of MO (a.u.) | -19.23659 | -1.16099 | -0.56233 | -0.51277 | -0.36997 | 0.02992 | |
| MO structure |  |
 |
 |
 |
 |
| |
| Explanation of MO | The core 1s oxygen AOs combine to form this MO. It is a non-bonding MO and it is occupied. The MO is very deep in energy as it holds the core electrons. These are strongly attracted to the nucleus so they cannot be used in bonding - the MO is too low in energy to be used in bonding. | This MO is formed from the combination of the 2s AOs of carbon and oxygen. It is a bonding MO and it is occupied. The MO is deep in energy, however it is much higher in energy compared to MO 1. This is because these electrons occupy a higher shell and therefore are less strongly attracted to the nucleus. | This MO is formed from the combination of the 2s AOs of carbon and oxygen. This MO is antibonding and it has 2 nodes. It is occupied. In bonding, it would destabilise the bond formed because it is antibonding. | This MO is formed from the combination of the 2px and 2py AOs of the oxygen atoms. It is bonding and occupied. These orbitals are degenerate as they have the same energy and structure. It is quite high in energy, therefore these MOs are used in bonding. As this is a bonding MO, it would stabilise the bond formed. | This is the HOMO (highest occupied molecular orbital). It is formed from the combination of the 2px and 2py AOs of the oxygen atoms. It is antibonding and occupied. This MO would destabilise the bond formed in bonding as it is antibonding. | This is the LUMO (lowest unoccupied molecular orbital). It is formed from the combination of 2px and 2py AOs of carbon and oxygen. It is antibonding and unoccupied. This MO would destabilise the bond formed in bonding as it is antibonding. |
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 4.5/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES - MO6 results because of mixing the orbitals you mentioned and the 2p-orbitals of O with the 2s on C. The latter combination is more predominant, so this would be a bonding and not an anti-bonding orbital. You correctly identified the AOs contributing to MOs 10 and 11 and that they are combined out-of-phase. However looking at the MO diagram reveals that there is no overlap of the orbitals, so this MO is non-bonding rather than anti-bonding. MOs 12 and 13 would destabilise the bonding if they were occupied.
Independence 1/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or Do some deeper analysis on your results so far