Rep:Mod:Andy1236

Physical Computational Lab - Transition states

Cope Rearrangement

The cope rearrangement is a [3,3]-sigmatropic shift reaction which proceeds through a concerted cyclic transition state (pericyclic reaction). It is a six electron process and so is allowed under thermal activation.

The starting product was modelled using a Hartree Fock method, the command line:

"# opt HF/3-21G"

The anti and gauche conformations of the molecule were modelled, prior to the calculations finishing, one would expect the gauche conformer to be higher in energy due to steric reasons (the groups on each end want to be furthest from each other).

	Anti	Gauche
Molecule
Dihedral / °	176.926	63.677
Energy / Hartrees	-231.6926024	-231.6915304
Point group	Ci	C2

Clearly following these calculations, the relative energies of the conformers is in disagreement with the expected result, the gauche conformer is lower in energy. The energies match exactly with the molecules in appendix 1, where the anti conformer matches "Anti1" and the gauche conformer matches "Gauche2", the point groups are also in agreement.

Next the conformer with C_i symmetry was optimised using the same method, the resulting geometry was then submitted to optimise using a DFT method, the command line was:

"# opt b3ylp/6-31G(d)"

	Hartree-Fock	B3YLP/6-31Gd
Molecule
Energy	-231.6925353	-234.6117011
Bond 1-2	1.32	1.33
Bond 2-3	1.51	1.5
Bond 3-4	1.55	1.55
Bond 4-5	1.51	1.5
Bond 5-6	1.32	1.33
Dihedral 1-2-3-4	114.66	118.48
Dihedral 2-3-4-5	180	180
Dihedral 3-4-5-6	114.66	118.48

The largest difference in the geometries of the HF and DFT methods is the dihedral angles moving to DFT has left the middle angle at 180° (pureky anti) and opened the end dihedrals by 2°. There was also a small difference in the bond lengths, proving that there is a need for higher level calculations to get an accurate representation of the lowest energy geometry.

It is not a good comparison to compare energies between methods so the actual energy values will not be compared. To compare the higher level calculation energy value to experimental values additional calculations need to be performed, a frequency test was submitted using the command line:

"# freq b3ylp/6-31g(d)"

The resulting file contained 42 vibrations for the molecule which were all positive thus the optimised structure is at a minimum. Thermochemistry results are summarised below:

Energy / Hartree	298.15K	0K	Meaning
Sum of electronic and zero point energies	-234.469194	-234.468774	Potential energy at 0K
Sum of electronic and thermal energies	-234.461846	-234.468774	Adds energy from vibration, rotation and translation at defined temperature
Sum of electronic and thermal enthalpies	-234.460902	-234.468774	Correction for H=E+RT
Sum of electronic and thermal free energies	-234.500774	-234.468774	Entropy contribution correction

Note that the frequency calculations were run at 1 atmosphere in both cases (298.15K and 0.000001K). The standard frequency calculations run at 298.15K and 1 atmosphere, to alter these conditions a modification of the .gjf was added, the commandline was changed to:

"# freq=readisoptopes b3ylp/6-31g(d)" instructs the program to read additional information at the end of the file.

Then the additional information was added - this was temerature and pressure and isotopic mass of each atom. This means that the temerature that the calculation is run at can be manipulated. For the calculation at 0K the information at the end was set to:

0.0 1.0 ie 0K and 1 atmosphere.

This returned an odd result (not one where all values are equal due to no thermal energy) where it was discovered that infact the calculation had run at 298.15K (with an input temperature of 0 the calculation reverts to standard 298.15K). The temeperature was set to a value very close to 0K (0.0001K) to see if the expected result occured, obviously from the table the expected result is observed with all energies being equal.

Optimizing the "Chair" and "Boat" Transition Structures

To start this section the allyl fragment was optimsed as before using the HF/3-21G then B3YLP/6-31G(d) for accuracy. 2 of these fragments are then loaded into 1 molgroup file and positioned 2.2Å apart in the correct orientation. The TS was optimised in 2 ways, firstly to a TS (Berny) by doing a Opt + Freq calculation, this essentially creates a negative frequency so a maximum on a PES which can be considered the TS. This was run at the Hartree-Fock level of theory and the command line used was:

"# opt=(calcfc,ts,noeigen) freq hf/3-21g" DOI:10042/to-2019

Negative Vibration	Vibration
Frequency / cm-1	-818
Energy / Hartree	-231.6193224
Forming bond 1 length / Å	2.02
Forming bond 2 length / Å	2.02

The second optimisation method was to freeze the coordinates of the atoms where the bonds will be forming and optimise the structure around this. After the structure has optimised, the structure is optimised and the full normal Hessian is calculated between the coordinates. The command line used was:

"# opt=modredundant hf/3-21g" DOI:10042/to-2021

The coordinates from this optimisation were then used with the command line:

"# opt=(ts,modredundant,noeigen) freq hf/3-21g" DOI:10042/to-2026

This yielded the optimised transition state without calculating the force constants.

Negative Vibration	Vibration
Frequency / cm-1	-818
Energy / Hartree	-231.61932184
Forming bond 1 length / Å	2.02
Forming bond 2 length / Å	2.02

The 2 methods converge well and in fact give the same length for the bond forming distances. In addition the final energies are extremely close and the negative vibration is of the same frequency. Both these are chair conformations, the next step will calculate the boat conformation of the transition structure.

The QST2 method was used where the calculation will interpolate between the reactant and product structures to try to find the transition state between them. The reactant (left) and product (right) are shown below and the transition state was found between the 2 structures.

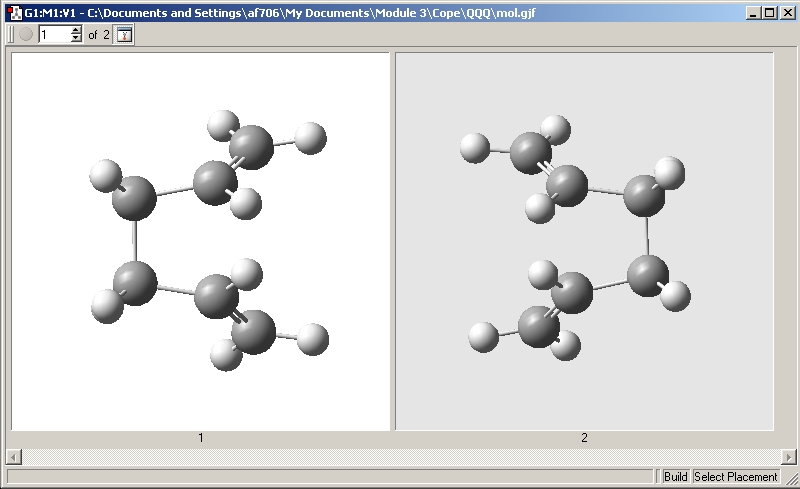
The command line used was:

"# opt=qst3 freq hf/3-21g" DOI:10042/to-2034

Negative Vibration	Vibration
Frequency / cm-1	-840
Energy / Hartree	-231.60280232
Forming bond 1 length / Å	2.14
Forming bond 2 length / Å	2.14

Intrinisic Reaction Coordinate Method

This method takes the transition state structure then alters the geometry in small steps to find a path to the product from the transition state. It follows the steepest path on the PES, the number of point to be plotted can be defined in the command line and 60 were used in these calculations. The calculation was run to calculate force constants always. The resulting calculation used 17 points to reach a minimum:

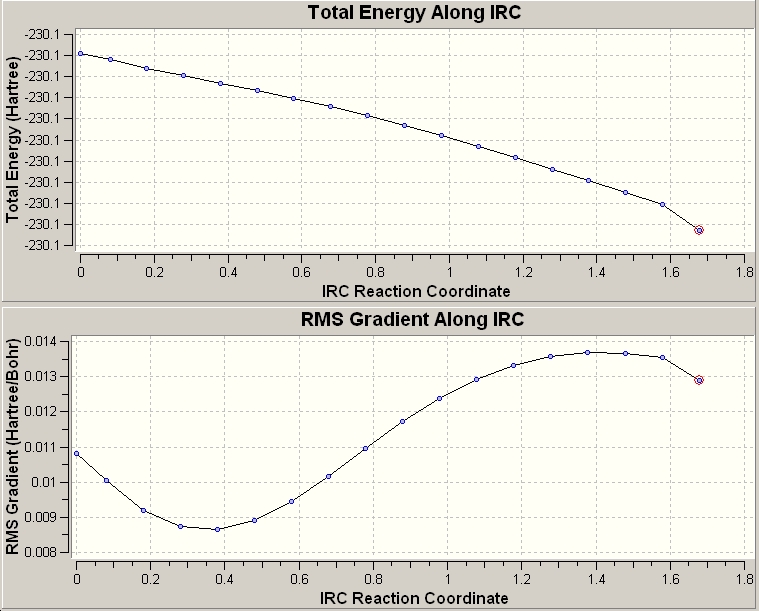
Activation Energy

Before any energy comparisons were made, a higher level of theory is required to accuratly represent the underlying energies. Thus the molecules were optimised using B3YLP/6-31G* methods, which resulted in energies much different from the Hartree-Fock method.

Below is a comparison of the reactant, chair and boat TS conformer energies from the B3YLP/6-31G* level at 298.1K and 1atm.

	Reactant B3YLP	Chair B3YLP	Boat B3YLP
Sum of electronic and zero-point Energies	-234.469194	-234.414927	-234.402342
Sum of electronic and thermal Energies	-234.461846	-234.409005	-234.396007
Sum of electronic and thermal Enthalpies	-234.460902	-234.408061	-234.395063
Sum of electronic and thermal Free Energies	-234.500774	-234.443813	-234.431098

Activation energies were calculated from the "Sum of electronic and zero-point Energies" values because the experimental values were at 0K so no thermal energy was taken into account. These values were:

	Chair	Boat
Hartree	0.054267	0.066852
Kcal/mol	34.0530309	41.95023167
Experimental	33.5 ± 0.5	44.7 ± 2.0

On comparison of the calculated activation energies and the experimental values it is clear that they are quite close and thus at the B3YLP level a good approximation of the activation energy is obtained.

The next important point is the comparison between the 2 levels of theory used, since if a certain level is sufficent to accurately predict close to experimental values, the added computational efficinecy over a higher level theory is useful.

Diels Alder Cycloaddition

This section looks at the cycloaddition pericyclic reaction between Cis-butadiene and ethene. Firstly the reactants were drawn and optimised using the semi-empirical AM1 method, the command line used was:

"# opt freq am1"

Ethene

Cis-butadiene

The orbitals were visualised and the symmetries deduced :

Ethene HOMO: Symmetric, LUMO: Antisymmetric

cis-butadiene HOMO: Antisymmetric, LUMO: Symmetric

Molecule	HOMO	LUMO
Ethene
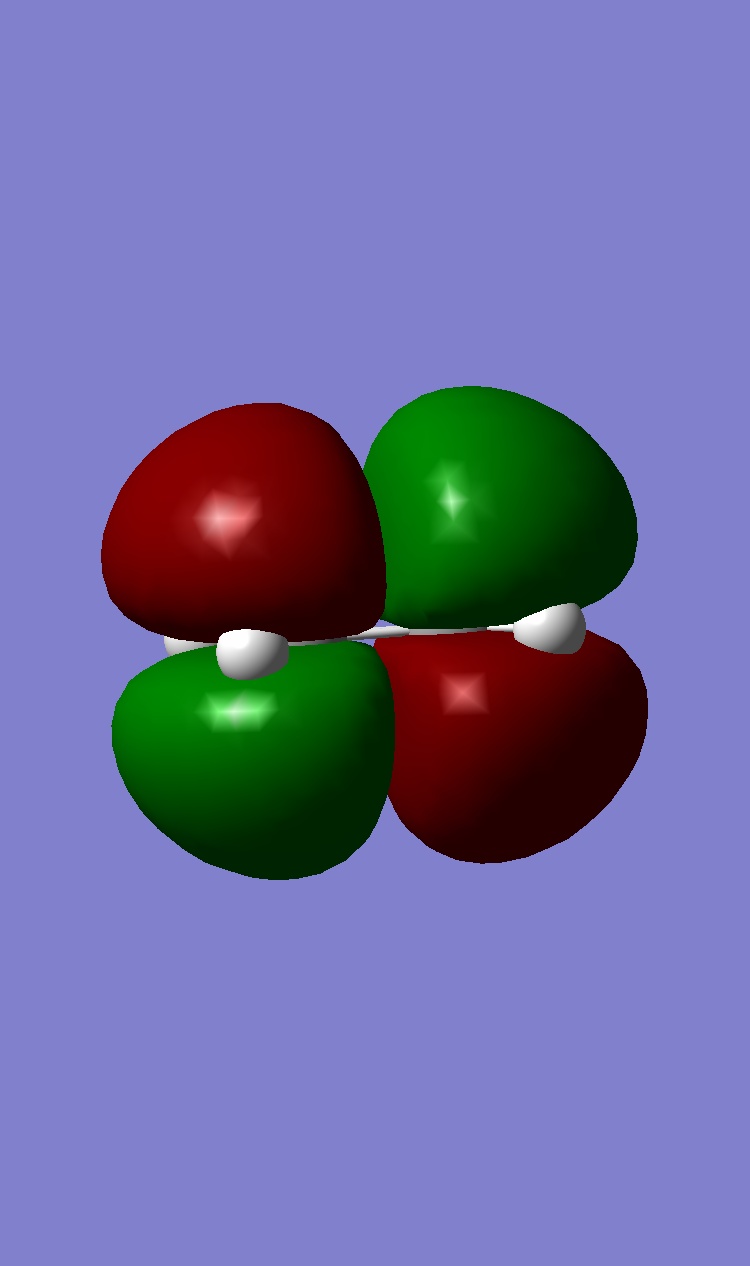
Butadiene

To calculate the transition state structure and observe the negative vibration the freeze coordinate method was employed as before. The distance between the atoms where the bonds were formed was set manually to 2.2Å and frozen, the resulting structure had hydrogens bending away from the forming bond. A Hartree-Fock method was used with a 3-21G basis set for a greater accuracy given that these calculations are reatively quick.

The opt and freq calculation was then run, to yield the final structure and transition frequency (-818cm^-1).

HOMO	LUMO

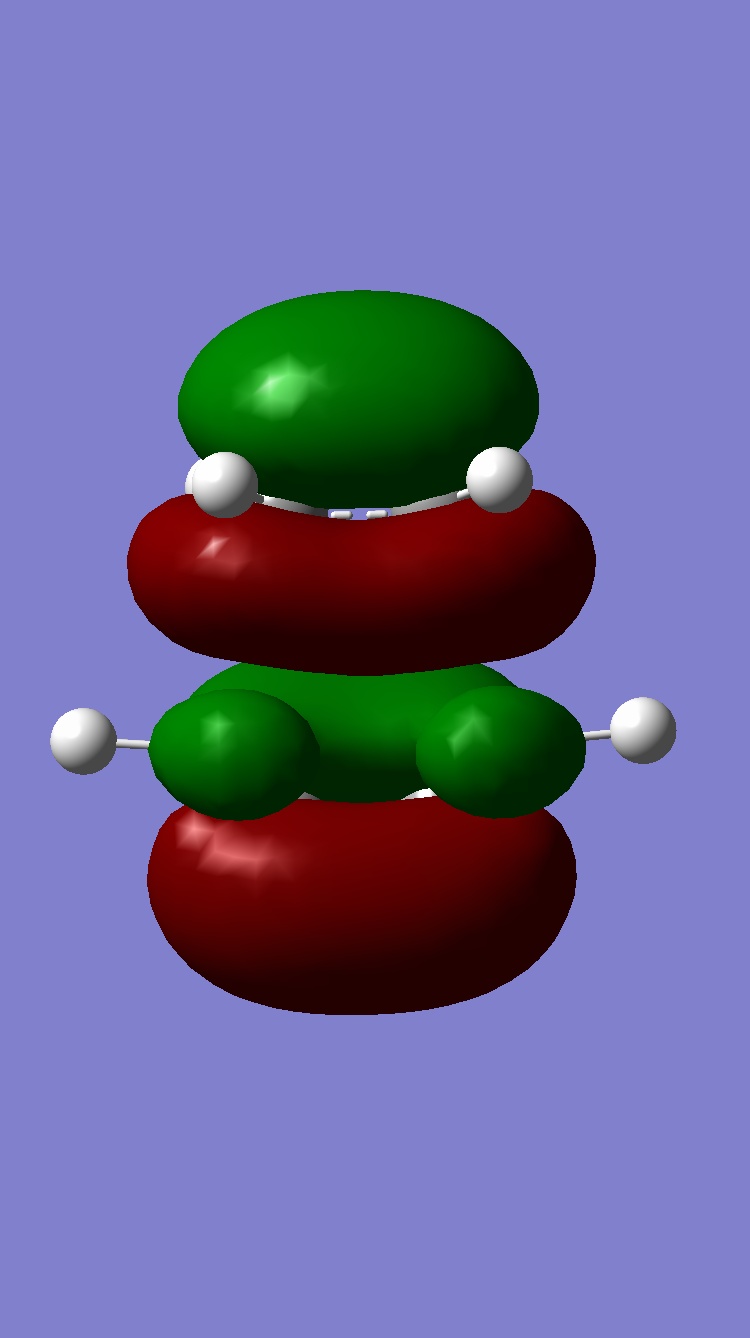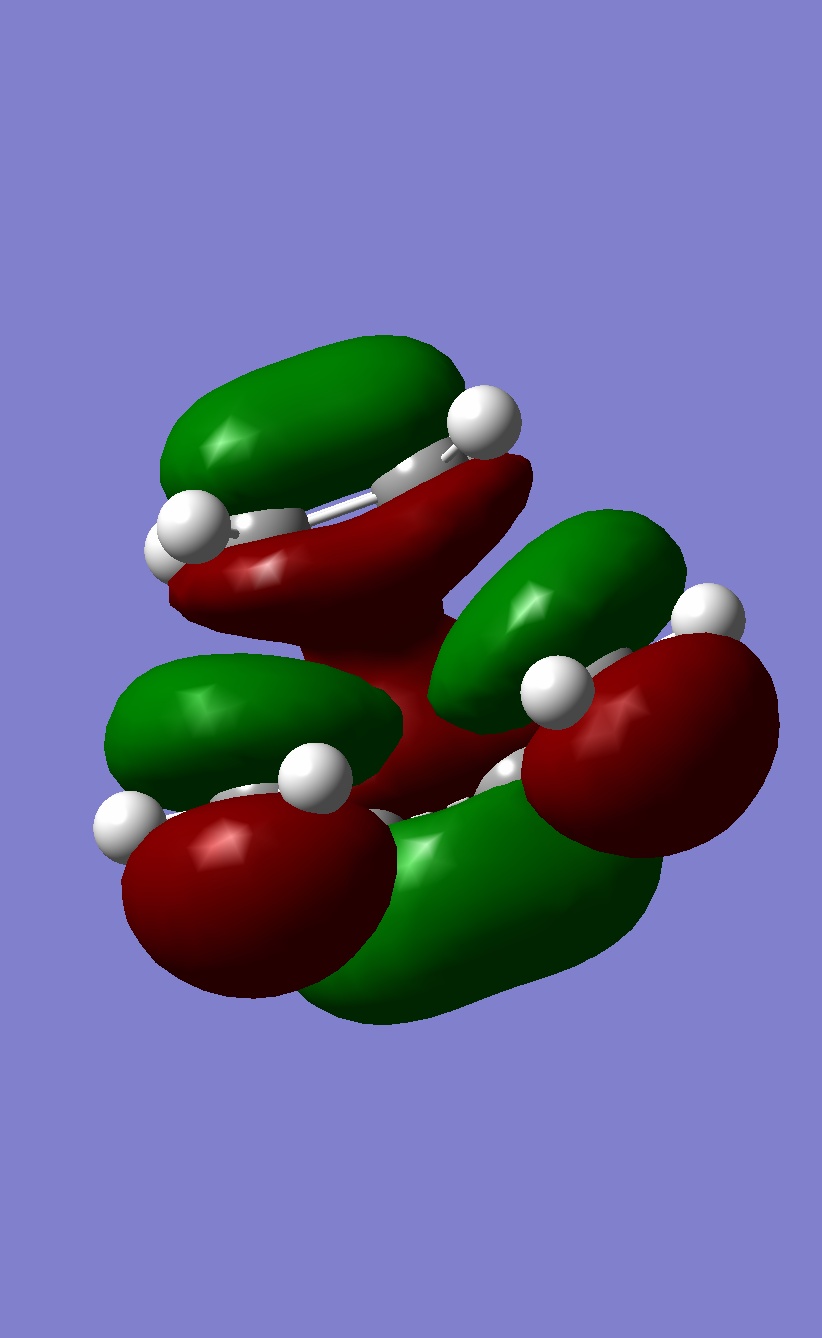
Both the HOMO and LUMO are symmetric with respect to a verticle plane through the centre of the molecule orthogonal to the screen. If we consider the HOMO - LUMO overlap of ethene and cis-butadiene, the overlap must be constructive thus the symmetry must be the same for "reacting" orbitals. It is thus expected the TS HOMO/LUMO symmetries are a product of the reactant symmetries. S*S=S and AS*AS=S (S=symmetric and AS=Antisymmetric). The forming bonds in the TS were measured and found to be 2.21Â in both cases (as expected for a concerted pericyclic reaction) this bond length is significantly longer than the average C-C bond distance (1.54Â). This said, the distance was less than the sum of the Van der Waals radii suggesting some sort of covelant bond (not formally a bond) is present. In the negative frequecy showing the transition movement it is clear that the distance between atoms creating new bonds is decreasing thus indicating a bond being formed. Also as expected in this transition vibration the formally double bonds in the butadiene are lengthening as they move towards the ethene (becoming single bonds) and the central C-C bond of butadiene is shortening (becomes a double bond).

It was noticed that the HOMO had a node between the 2 reacting molecules in the transition state. This idicates that there is no bonding interaction here from the HOMO, clearly this cannot be correct if the bonds form on inspection of the HOMO-1 a clear bonding MO was observed between the 2 molecules. Thus it is not the HOMO of the transition state that forms the final bonding MO in the product.

HOMO-1 of the transition state

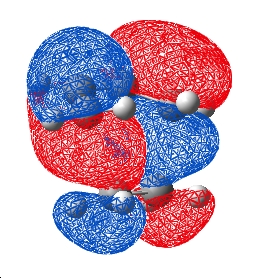
Due to the abnormality of the HOMO nodal plane in the hartree fock optimised structure, a transition state calculation at a higher level of theory was performed. The freeze method was used with MP2/6-31G* level theory for frequencies and optimisation. This time the HOMO was as below:

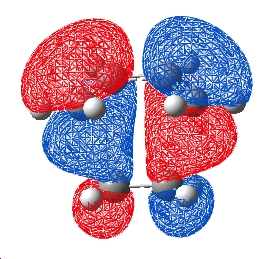
In fact the ordering of the HOMO/HOMO-1 has changed and thus the HOMO has the bonding interaction between the 2 molecules. This shows that it is important to use higher levels of theory when looking at MO's to ensure that an accurate result is given. The distance between the 2 atoms where the bonds form was 2.28Å with the MP2 method, longer than the hartree fock level prediction.

Cyclohexa-1,3-diene in a Diels-Alder reaction

This cycloaddition reaction has the potential to have an endo or exo product depending on the relative orientation of the approaching molecules before reaction. It is reported that this cycloaddition occurs via a kinetically controlled pericyclic reaction. Since the energy of the starting materials leading to endo and exo Ts' and products is the same, the most likely product is that which has the lowest barrier TS (smallest activation energy). Hence the only calculation that needs to be perfomed is an optimisation of the transition state structures (with a frequency calculation to observe the TS imaginary vibration). This was performed at HF/3-21G level using the freeze coordiante method.

Geometry

Exo	Endo
Vibration	Vibration
Vibration	Vibration

	Exo	Endo	Difference	Difference / Kjmol-1
Forming bond 1 / Å	2.26	2.23
Forming bond 2 / Å	2.26	2.23
Sum of electronic and zero point energies / Hartree	-605.408135	-605.414901	0.006766	17.764133
Sum of electronic and thermal energies / Hartree	-605.398675	-605.405475	0.0068	17.8534
Sum of electronic and thermal enthalpies / Hartree	-605.397731	-605.404531	0.0068	17.8534
Sum of electronic and thermal free energies / Hartree	-605.443688	-605.45013	0.006442	16.913471

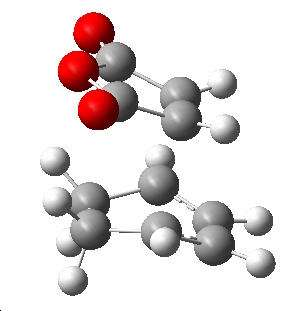
The lower energy transition state geometry was the endo structure, which is 17.76KJmol^-1 lower than the corresponding exo transition state at 0K. This means that if the reaction is under kinetic control, the endo product will be the major product. To rationalise this difference in energy the respective "attack" position of the maleic anhydride dienophile was considered:

Exo	Endo

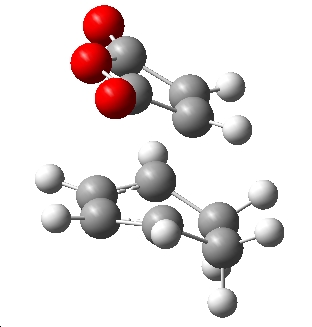
Clearly viewing from this angle shows that in the exo TS, the ring of the maleic anhydride lies over the non-planer sp³ carbons thus there is some repulsion from the hydrogens facing towards the maleic anhydride. Conversely in the endo TS, the maleic anhydride is above the planer sp² carbons in the diene thus with no hydrogens facing it. In conclusion, the "attack" approach for maleic anhydride for the exo is relatively hindered compared to the endo geometry, supporting this argument is a comparison of the distance between atoms where the new σ-bonds are forming. In the exo TS where some hinderance is observed the forming bond length is slightly longer (2.26Å) than the respective endo length (2.23Å). This is a possible explanation for the difference in TS energies, and a reason why the endo product may be the predominante product.

Molecular orbital discussion

	Exo	Endo
HOMO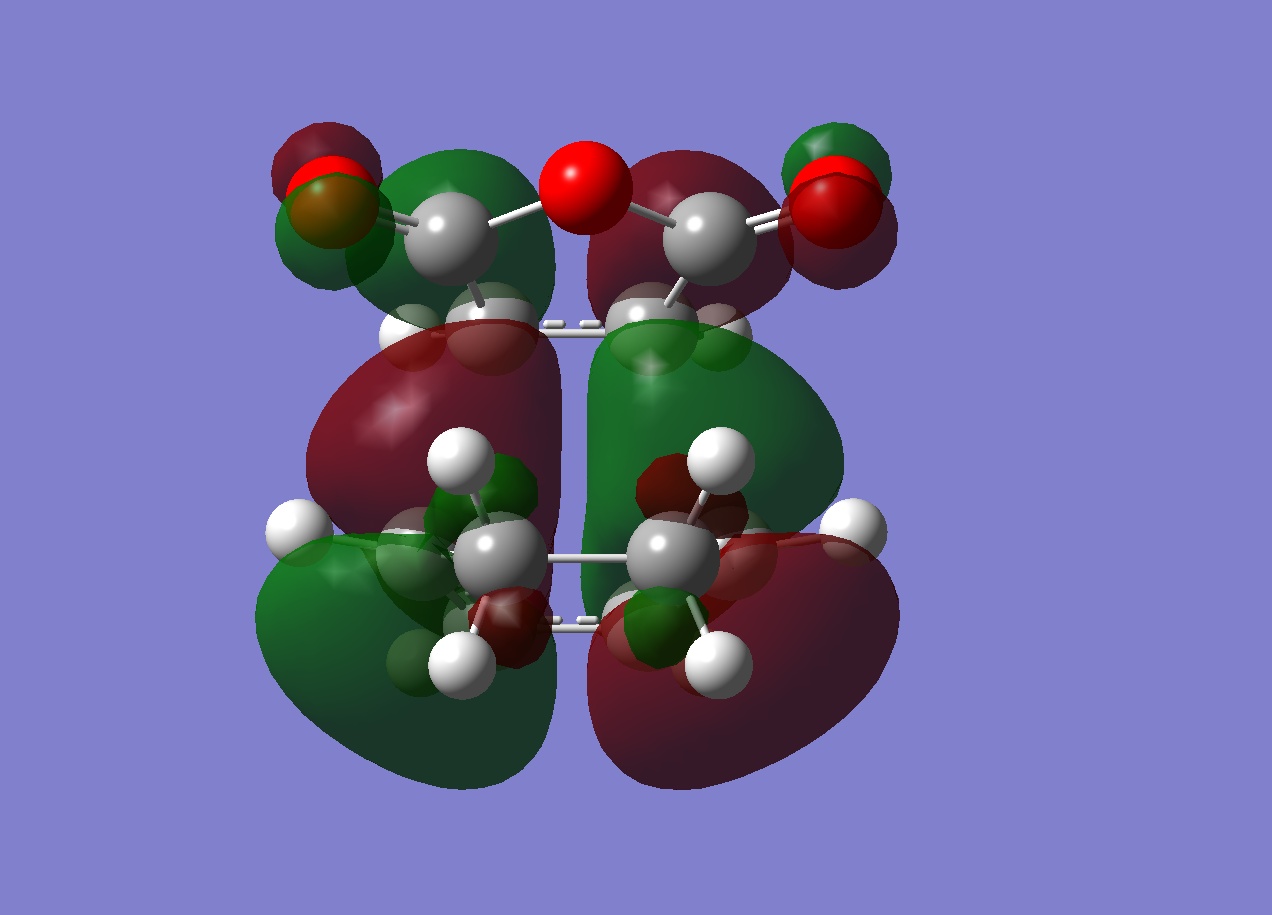
LUMO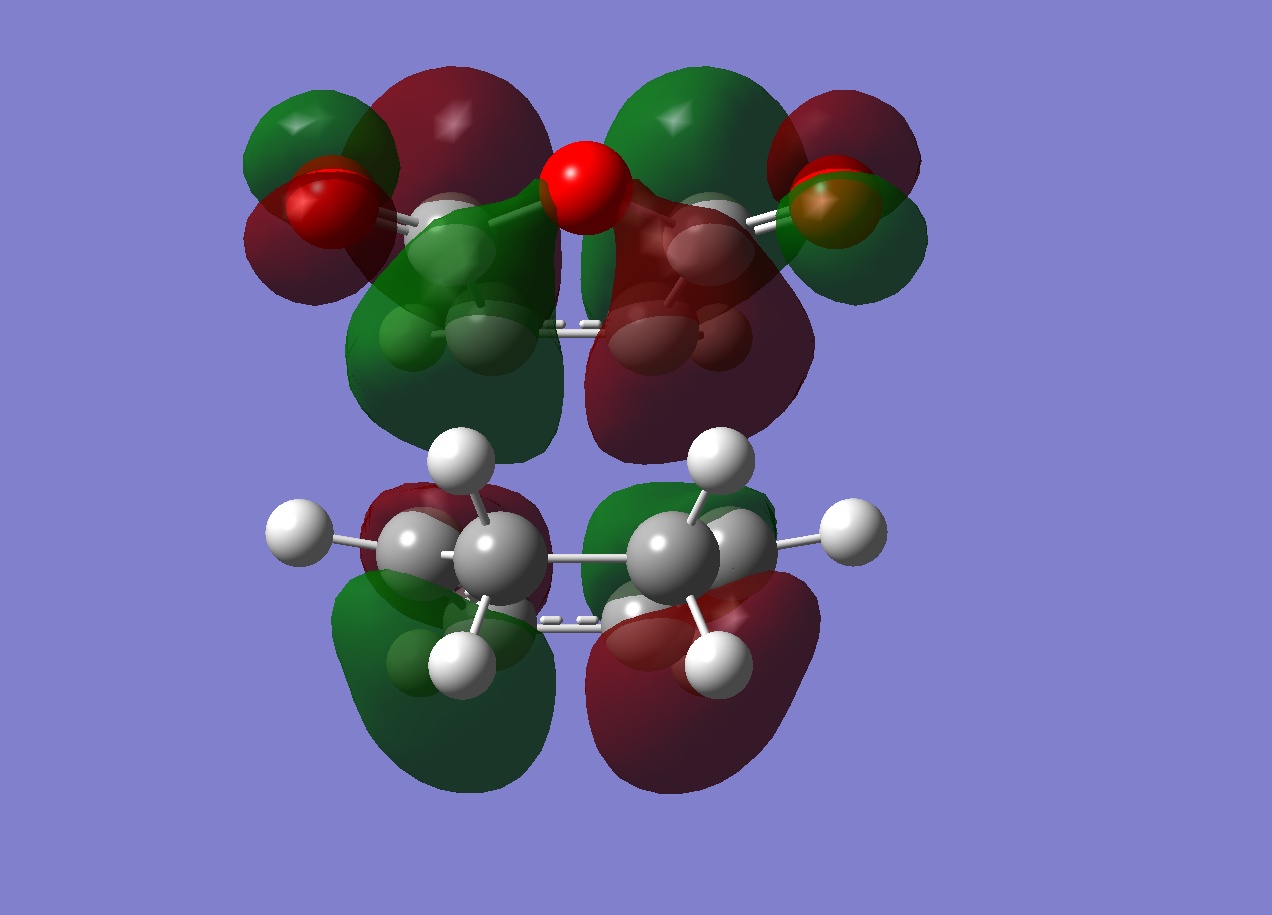

Exo

HOMO:Antisymmetric

LUMO:Antisymmetric

Endo

HOMO:Antisymmetric

LUMO:Antisymmetric

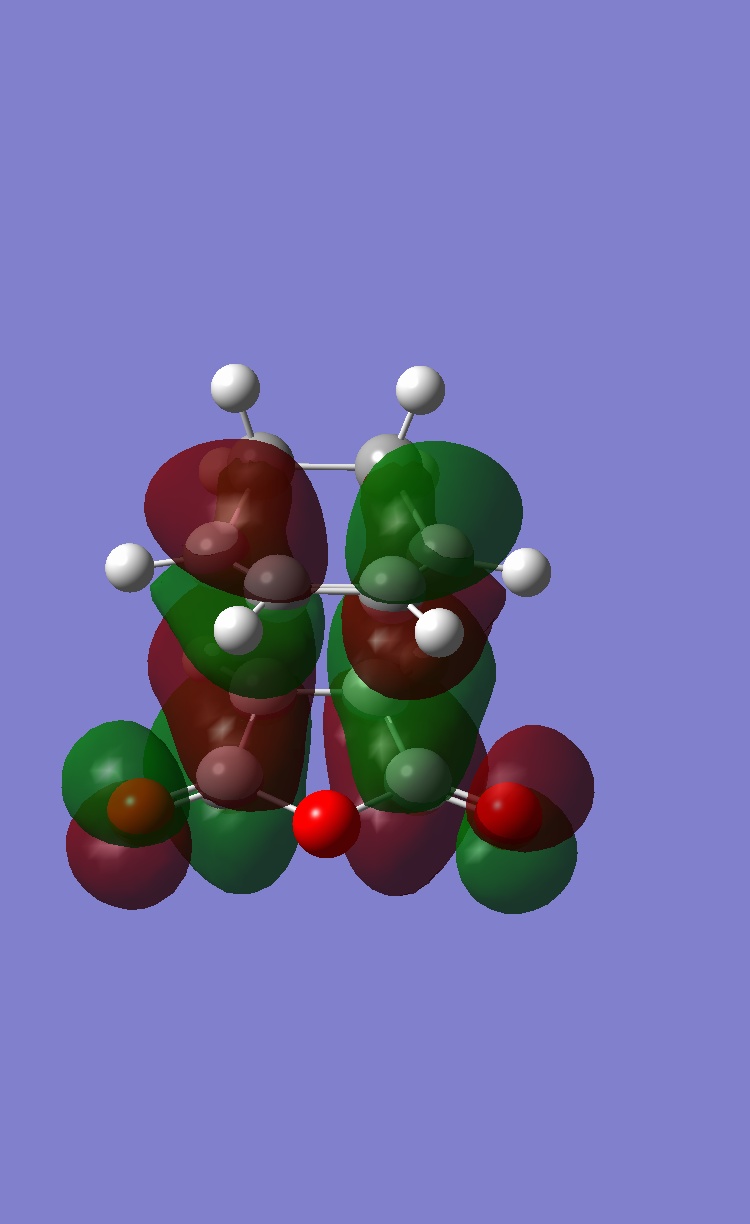
Another explanation for the preference for endo over exo is "secondary orbital overlap" - this is based on a frontier molecular orbital theory. It predicts that the endo TS is favoured by a stabilising interaction between "orbitals" which are not related to the formation of the new bonds. This theory is somewhat at odds with the calculations because it is based on frontier orbital theory. It describes orbitals via localised areas of electron density where 2 orbitals located on the ends of the diene interact with 2 orbitals of the ene function in the maleic anhydride accompnied by the secondary interaction of 4 more orbitals. The actual fact is that there are no localised orbitals and just the interaction of the (single orbital) HOMO of the diene with the (single orbital) LUMO of the maleic anhyride. For the secondary orbital theory to be correct the resulting HOMO should have electron density between the reacting centres and some density between the other centres in each molecule (shown below)

Endo transition state showing interacting frontier orbitals of the HOMO from the diene and LUMO of maleic anhydride

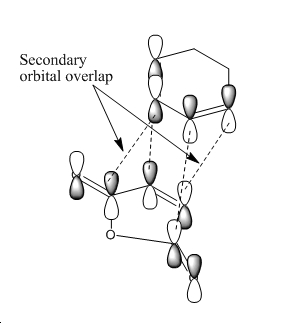
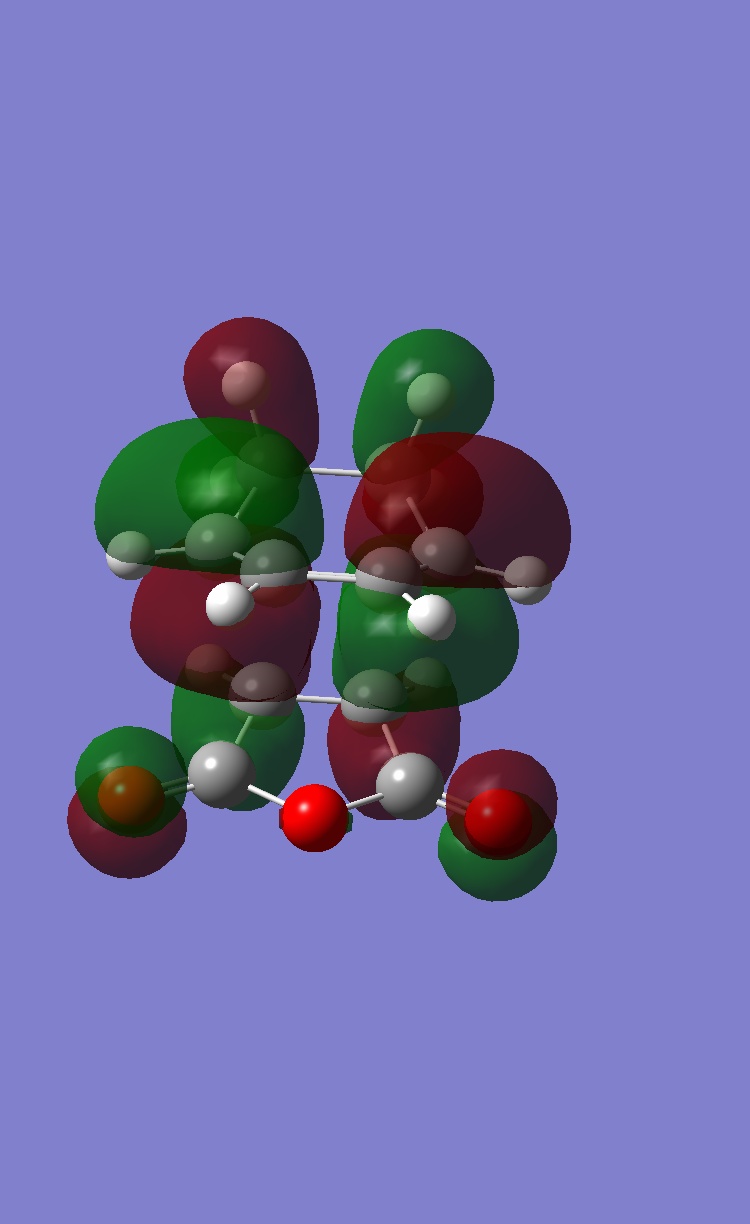
Thus the HOMO molecular orbital calculated should show an area of electron density between the secondary centres implied above. Looking at the HOMO calculated from hf/3-21G methods shows no such area of electron density. The HOMO-1 and HOMO-2 of the endo TS were then visualised to see if any such interactions in these MO's, infact some density was observed between the two molecules other than between the centres forming the σ bonds in the HOMO-1. These are shown below:

HOMO	HOMO-1

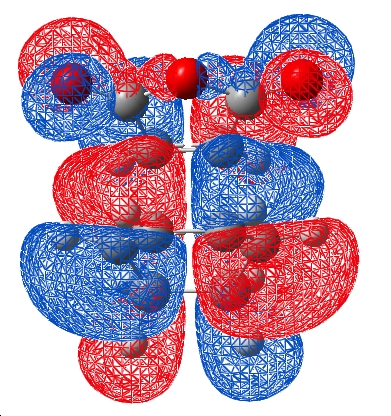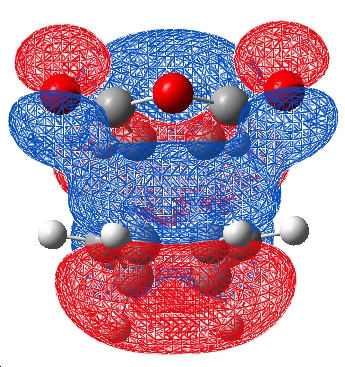
Although this is observed in the HOMO-1, it is not between the centres predicted by frontier orbital theory (carbons) in fact it is between the carbonyl oxygens on the maleic anhydride which are "bound" to the expected carbons, this interaction is unexpected. When compared to the exo TS HOMO and HOMO-1 a stark difference is obvious:

HOMO	HOMO-1

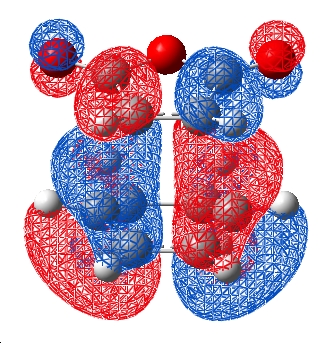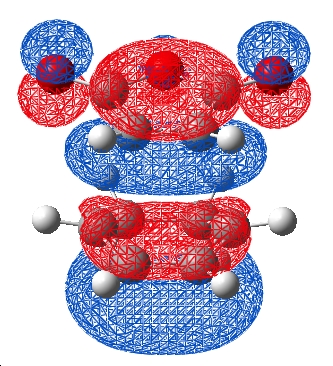
In both cases it is noticed that the symmetry of the HOMO-1 is symmetric in both exo and endo cases.

The exo HOMo still shows the "primary" interaction between the reacting centres but now the HOMO-1 shows NO electron density between the 2 molecules. As a result there will be no other interactions between the maleic anhydride and diene.

In conclusion to this molecular orbital analysis, the primary interaction is clear in both endo and exo cases with a large area of electron density between them. When "secondary" interactions are considered in the HOMO it appears that neither the exo or endo TS posess this predicted interaction. On closer inspection of the deeper orbitals, a seconday area of electron density between the maleic anhydride and diene was observed in the HOMO-1 for the endo TS but this was not present in the exo TS. This could then constitue a secondary interaction and explain why the endo TS is lower in energy, although it is not in agreement with the frontier molecular orbital prediction (the actual density is between carbonyl oxygens as opposed to the carbonyl carbons and the middle carbon atoms of the diene).

To make sure that the calculation level was high enouigh to be giving results that allow these conclusions to be drawn, the same optimisation of the TS was performed at MP2/6-31G* level. This is a much higher level of theory and thus if its results are concurrent with the lower level theory will show that this is a valid MO prediciton to base these arguments on. Following the optimisation of the TS t MP2 level, the MOs and geometry were almost exactly the same as the hf/3-21G level. This conferms that the arguments based on these geometries and MOs are valid and remain consistent to the MP2 level.

Does the reaction of a Pyrido Isoindole with a electron deficient alkene occur via a cycloaddition or zwitterion intermediate pathway?

It is known that the reaction of a Pyrido Isoindole (diene) and dimethyl fumerate (dieneophile) is exo selective. Reasons for this are unclear, two reasons have been suggested:

• Synchronous cycloaddition
• Stepwise process through zwitterionic intermediates

Originally the stepwise process was suggested in 1976 by S.Ikeda et al but this was then revised in 1985 by S.Kajigaeshi et al suggestig a synchronous cycloaddition pathway (shown below)

Reaction scheme of the suggested cycloaddition reaction of the Pyrido Isoindole with dimethyl fumerate

The top product (exo) is formed in 7:3 favour over the endo product. The paper suggests that the exo selectivity "might be a result from the 8π+2π concerted cycloaddition".

Reaction scheme of the original pathway via the zwitterionic intermediate B

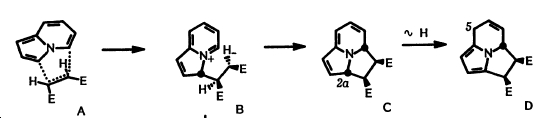
The zwitterionic pathway clearly shows 1 bond forming before the other via an intermediate. This can be through of as entirely asynchronous.

The aim of this computational study will be to confirm wether S.Kajigaeshi et al are correct in assigning a "synchronus cyclization pathway". The first step was to model the transition state so that the bond forming can be observed, a DFT method was used - specifically the B3YLP/6-31G* to optimise the TS structure (using the frozen coordinate method). Distances between the atoms where the new bonds are forming was set to 2.2Å (closer than the sum of the Van der Waals radius but further than the average distance of a C-C bond).

Note that only 1 transition state was modelled due to time constraints, but it is assumed the synchronicity will remain constant regardless of approach of the dieneophile.

The forming bond distances featured a large difference in magnitude, which is an indicator that the bond formation is NOT synchronous. One distance (the closer) is 1.836Å versus the other distance at 2.65Å, clearly a large difference in the forming bond lengths indicates that the bond formation is not happening equally thus in an asynchronous fashion.

Next the negative vibration (imaginary) was inspected, this shows the vibration associated with the "bonds forming", the result is very clear... that one bond is forming far before the other (hugely asynchronous) this could almost suggest that the reaction occurs via the zwitterionic intermediate rather than the concerted reaction pathway - the opposite of the published conclusion. In any case, the DFT model shows that bond formation is deffinately not synchronous.

With more time, the other (endo) transition state could be modelled and a comparision of the two could be made. Also a closer study of the potential intermediates may give an explanation of the high exo selectivity of the reaction (unknown to the authors).

In conclusion, had these modeling techniques been avaliable to the authors who published this paper, a simple calculation (nowadays) would have shown that infact the reaction is not synchronous and thus ruled out their explanation for exo stereoselectivity.