Rep:Mod:Andy1234

Computational Chemistry Lab Course 2009

Module 1: Structure and spectroscopy (Molecular mechanics and molecular orbital)

Molecular mechanics (MM) modelling uses Newtonian mechanics to model a molecular system, 3 assuptions are included at this level:

1. Each atom is modelled as a single particle
2. Each atom has a defined radius, constant net charge and polarisability
3. Bonds between atoms are defined using an equilibrium bond length which is determined experimentally

MM models sum 5 potential functions to calculate the molecular systems potential energy, these are assumed not to interact and consist of:

1. Equilibrium bond distances between atoms
2. Ideal bond angles between atoms
3. Ideal torsional angles between atoms
4. Electrostatic interactions between atoms
5. Van der Waals interactions between atoms

These potential functions are then minimised by optimising the listed parameters, and thus geometry of the molecule, to achieve an energy minimum. Limitations to the method of modeling occur as a result of the use of experimental data in parameters of the molecule. This means that for a molecule to be investigated, it must have a set of perviously obtained parameters, limiting the usage of MM models. The vast simplifications of the model also make absolute energy calculations difficult, its strength lies in comparitive analysis.

The Hydrogenation of Cyclopentadiene Dimer

1,3 cyclopentadiene dimerises, proceeding via a [_π4+_π2] cycloaddition reaction. This concerted process can proceed to give 2 different isomeric products, the endo or exo dimer.

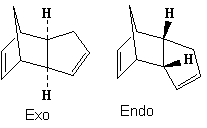
Endo versus Exo

Dimerisation products

Potential function	Exo Dimer	Endo Dimer	Difference
Stretch	1.2884	1.2445	0.0439
Bend	20.5774	20.827	-0.2496
Stretch-Bend	-0.8386	-0.835	-0.0036
Torsion	7.6802	9.5206	-1.8404
Non-1,4 VDW	-1.4281	-1.5439	0.1158
1,4 VDW	4.2359	4.3397	-0.1038
Dipole/Dipole	0.378	0.4486	-0.0706
Total Energy (kcal/mol)	31.8932	34.0015	-2.1083

Cyclopentadiene dimerises to produce specifically the endo dimer rather than the exo dimer. The above table shows the energy breakdown and total energy of the 2 dimer products. The exo product is 2.1083 kcalmol^-1 higher in total energy than the exo product which indicates that the exo product is actually more thermodynamically stable. The main energy difference in products was the torsional strain energy, where the exo product was 1.8404 kcalmol^-1 more stable. This energy difference can be attributed to the difference in torsional strain across the newly formed C-C bond. The endo product had an average 48° dihedral angle across the new C-C bond which is a gauche conformation, compared to the exo product with a average 177.5° angle - an antiperiplaner conformation. The elevated steric strain of a gauche conformation compared to the antiperiplaner arrangement explains the energy difference, there may also be a stereoelectronic effect whereby the C-C_σ overlaps with the antiperiplaner C-C_σ* although this effect will not be dominant due to the energy difference between the σ and σ* orbital energy and relatively non-polarised bonds.

One would expect under thermodynamic conditions that the lower energy product (exo) would be formed, but it is known that this is not the case suggesting that the reaction is under kinetic control for the kinetic product (endo) to form. The reason for this kinetic control can be derived from seconday orbital interactions of the 2 cyclopentadiene reactants, where favourable secondary orbital overlap between centres that are not bonded in the adduct result in a lowering in the endo transition state energy. To fully appreciate this stabilisation one must consider the frontier molecular orbitals of the diene and dienophile, a constructive interaction develops as they approach between the 2 orbitals located on the carbons not forming a new bond. This results in the endo product forming faster and thus as the major product.

Once the endo dimer is formed, it can be hydrogenated, the energies of the different hydrogegenation products can be compared to investigate which is the more thermodynamically favoured.

Hydrogenation Regiospecificity

Hydrogenation Dimers

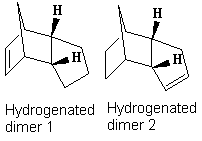
Potential function	Dimer 1	Dimer 2	Difference	% contribution
Stretch	1.24	1.09	0.15	3.13
Bend	18.91	14.56	4.35	91.17
Stretch-Bend	-0.76	-0.55	-0.22	-4.54
Torsion	12.15	12.5	-0.35	-7.38
Non-1,4 VDW	-1.51	-1.09	-0.41	-8.65
1,4 VDW	5.74	4.51	1.23	25.8
Dipole/Dipole	0.16	0.14	0.02	0.47
Total Energy (kcal/mol)	35.93	31.16	4.77

The MM2 calculations show that product 2 is the thermodynamic hydrogenation product with a total energy 4.77 kcalmol^-1 lower than product 1. It is clear that the main contribution to the difference in total energy is the bend energy, with a 91% contribution to the energy difference. The large difference is due to the relative release of strain of the sp² centre in a pentane ring versus directly adjacent to an already strained bridge head. The larger stabilisation occurs from releasing the strain from the sp² centre closest to the bridge head, thus product 2 is formed.

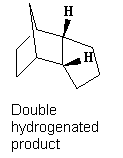
Tetrahydrogenation

Double hydrogenation Dimer

Potential function	Dimer
Stretch	1.1899
Bend	14.8626
Stretch-Bend	-0.5543
Torsion	15.2365
Non-1,4 VDW	-0.6602
1,4 VDW	6.0349
Total Energy ( kcal/mol)	36.1094

It is also noted that the tetrahydrogenation product is formed only after prolonged hydrogenation, clearly from comparison of the energies of the tetrahydrogenation product with hydrgenation products 1 and 2, the total energy of the tetrahydrogenation product is notably higher and thus stability is decreased as both double bonds get hydrogenated. The main contributing factor is a large increase in torsional strain while only achieving a small decrease in bend strain. In addition 1,4 Van der Waals force contributions for the tetrahydrogenation product increased significantly over the single hydrogenation, this is due to the release of planarity across the molecule which results in hydrogens being brought closer together. Overall, the process is not thermodynamically favourable.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

In this experiment, MM2 calculations were run in ChemBio3D on 2 pyridinium reactants. The MM2 minimisation is iterative and can fall into "potential wells" where the optimisation reaches a local energy minimum, but not a global minimum. The result is a geometry optimisation which is not the lowest energy conformer, thus to achieve a better understanding of the global minimum energy optimisation, multiple start conformations were optimised.

The Grignard reagent was not able to be modelled by MM2 because there are no experimental values to model the atom with. ChemBio3d gave the error "No atom type was assigned to the selected atom!".

NAD+ analogue 1

NAD+ analogue 1

Conformational Energies

Potential Function	Conformer 1	Conformer 2	Conformer 3
Stretch	1.1739	1.155	0.9077
Bend	11.4995	11.3304	6.851
Stretch-Bend	0.0531	0.0518	0.1187
Torsion	4.9818	5.2852	9.5355
Non-1,4 VDW	-1.9484	-2.0917	-2.6605
1,4 VDW	11.906	11.845	11.502
Charge/Dipole	2.6556	2.692	3.1661
Dipole/Dipole	-3.9773	-3.9483	-3.8186
Total Energy (kcal/mol)	26.3442	26.3194	25.6019
Dihedral angle ° C=O - aromatic ring	23	27	41

The optimisation of this molecule fell into 3 potential minimums, these are recorded along with the respective dihedral angle between the C=O bond and aromatic ring. The most thermodynamically stable structure occurs where the dihedral angle is 41°, notably the bend energy decreases dramatically from the other conformations when in conformer 3 but this is accompanied by a slightly smaller increase in torsional strain. The result is a 2.7% difference between conformer 2 and 3.

Many different starting positions were tested, all of which resulted in the carbonyl at a positive angle (above) to the aromatic ring plane. The carbonyl was placed at a -80° torsional angle before MM2 optimisation was run, but the resulting optimised geometry still had a positive torsional angle (23°). Extreme positive starting dihedral angles ~90° were optimised, returning an angle of 27°. Only when an extreme positive starting angle and the carbon (highlighted in yellow) was moved below the plane of the ring did the optimisation return the geomtetry with a 41° torsion angle.

ChemBio 3D image showing the torsional angle between C=O and the aromatic ring

The stereospecificity of alkylation of Conformer 3

Reaction with MeMgI (Grignard)

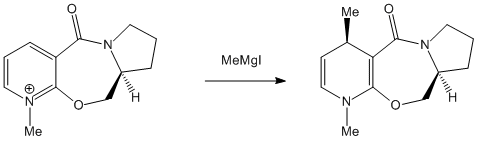
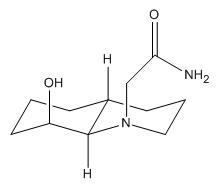
The specificity of the reaction can be attributed to a coordination effect between the electropositive Magnesium atom in the Grignard and the lone pair of the amide oxygen. Since the lowest energy conformer 3 has a dihedral angle of 41° between this oxygen and the plane of the aromatic ring, the Grignard will be directed to the top face as it coordinates. The image below shows the magnesium in pale yellow coordinating to the oxygen and the methyl being directed to the top face.

Image of the magensium coordinating to the carbonyl oxygen and thus directing methylation to the top face of the aromatic ring

NAD+ analogue 2

As with the previous starting product, MM2 was used to minimise the energy to achieve the optimised conformer.

Conformational Energies

NAD+ analogue 2

Potential Function	Conformer 1	Conformer 2	Conformer 3	Conformer 4
Stretch	1.5851	1.5675	1.7463	1.598
Bend	6.8062	6.4859	9.5513	7.2766
Stretch-Bend	0.3296	0.3396	0.3914	0.3466
Torsion	-6.1705	-6.0655	-6.2386	-6.0827
Non-1,4 VDW	-1.8181	-1.8344	-1.2462	-2.1555
1,4 VDW	17.5229	17.5243	17.9108	17.6791
Charge/Dipole	2.3712	2.3413	2.5591	2.3293
Dipole/Dipole	-4.8031	-4.797	-4.7922	-4.8531
Total Energy (kcal/mol)	15.8233	15.5616	19.8818	16.1382
Dihedral angle ° C=O - aromatic ring	-43	-42	45

Again for this starting product, the carbonyl was set at extreme dihedral angles to the aromatic ring both above and below. Energy minima were observed at dihedral angles -42° and 44°, the most stable being when the C=O is below the plane of the aromatic ring at an angle of -42°. Once the dihedral angle was set, further energy reductions were acomplished by controling the plane of the ring and isopropyl group adjacent to the carbonyl. Care was needed to ensure that the methyl group stil retained its absolute stereochemistry, but the 7 membered ring was completely inverted to get the C=O from above to below the ring plane.

The Stereospecificity of the reaction with PhNH₂

Reaction of NAD analogue 2 with PhNH₂

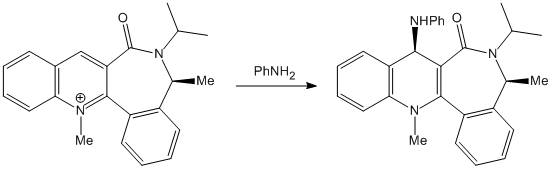
The reaction occurs via attack of the PhNH₂ which, contrasting reaction 1, has no coordinating ability. In addition it is relatively sterically hindered compared to the Grignard reagent in which the magnesium is small and relatively unhindered. This means that its attack of PhNH₂ will be directed mainly by steric interactions of the nucleophile with the environment of bottom versus top attack.

From the section above, it is clear that the most stable conformer (lowest in energy) is that when the C=O is below the face of the ring. The top face is then less sterically crowded than the bottom and thus the prefered direction of attack by PhNH₂, this leads to the up stereochemistry in the product as given in the reaction scheme.

Improvements on the MM2 Model

Firstly it is important to note that the MM2 model in ChemBio3D have been effective in predicting structures that can be rationalised when coupled with regio/stereo selectivity issues. It allowed the correct predictions of stereochemistry from optimised geometries in nucleophilic attack, which shows that is is a basic yet powerful program.

This said, it failed to model a simple Grignard reagent, on the basis that it did not have enough experimental data to accurately model it. This leads to the major downfall of a molecular mechanics model - that it can only operate within the parameters of things that have already been done.

Improvements to this model, without changing the method could include:

• Better approximations of the constituent potentials (a more detailed force field)
• Better iterative processes (essentially to speed optimisation up and prevent the "potential well" problem)
• More molecules parameters in the model.

Models based on Newtonian mechanics are fast and simple to dissect, but more complicated models will be more powerful in predicting properties and structures. Understanding and modelling the electronics of a molecule would be a much longer but more powerfull approach to these problems. For example, the molecular orbitals of the molecule could be calculated, giving information on electron density and relative HOMO - LUMO locations which allow predictions of things like nucleophilic and electrophilic attack to be much more precise and extrapolative.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

This experiment looks at a specific intermediate in the synthesis of taxol

Up Atropisomer

The "up" atropisomer

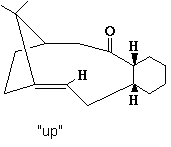
Potential Function	Up Boat Conformation	Up Chair Conformation
Stretch	2.7698	2.6979
Bend	16.5397	15.8394
Stretch-Bend	0.4477	0.3998
Torsion	20.6015	18.1548
Non-1,4 VDW	-0.3804	-0.9893
1,4 VDW	13.9529	12.6323
Dipole/Dipole	0.1766	0.1491
Total Energy (kcal/mol)	54.1078	48.8841

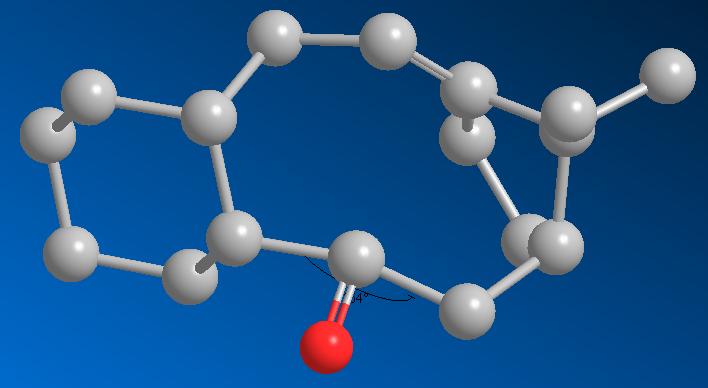
The initial structure was drawn into ChemBio 3D and a preliminary MM2 energy minimisation was run. This gave the “up” atropisomer with a total energy of 54.1078 kcal/mol. To try and optimise the structure further the 10 member ring was manipulated by moving atoms off their optimised positions and then running another minimisation. This made a tiny energy reduction which was of little consequence. It was then noted that the 6 member ring was in a almost "twist boat" conformation which is high in energy, the ring was manipulated into a chair like conformation and the MM2 re-run. This resulted in a notable decrese in total energy to 48.8841 kcal/mol (9.65% decrease), mainly consisting of decreases in bend, torsion and 1,4 Van der Waals energies. These can be attributed to the change from boat to chair conformations of the 6 member ring.

Flat Atropisomer

Potential Function	Flat
Stretch	4.3854
Bend	76.297
Stretch-Bend	-0.1017
Torsion	16.2547
Non-1,4 VDW	-1.399
1,4 VDW	23.6398
Dipole/Dipole	-0.0886
Total Energy (kcal/mol)	118.9876

The carbonyl group was then changed to down relative to the hydrogens on the 6/10 member ring carbons. After running the MM2 calculation again, the carbonyl was flat (neither up or down) giving a huge increase in energy (total energy was 118.9876 kcal/mol or a 58.9% increase in energy). The main contributing factor was the bend energy which increased 79.2% as the carbonyl became flat. When looking at the molecule, it is clear that the sp² centre is far from its ideal 120° bond angle. in fact, when the angle was measured it was 164°.

Looking at the "flat" carbonyl conformer with a bond angle of 164° across the sp² centre. Note, hydrogens removed for clarity.

Down Atropisomer

The "down" atropisomer

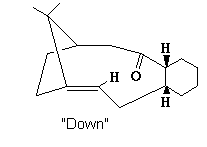
Potential Function	Down Boat Conformation	Down Chair Conformation	Down Chair + altered 10C ring
Stretch	5.9697	3.0676	10.6331
Bend	29.0881	15.0233	0.3117
Stretch-Bend	0.2587	0.3598	19.7852
Torsion	38.191	21.1612	-1.3707
Non-1,4 VDW	3.5831	-0.0597
1,4 VDW	21.7133	13.6669	12.5613
Dipole/Dipole	0.2371	-0.0454	-0.1812
Total Energy (kcal/mol)	99.041	53.1737	44.2941

The carbonyl was moved to a position where it pointed pown compared to the 6/10 membered ring hydrogens. After MM2 minimisation from this starting point, a large energy increase was observed with a total energy of 99.041 kcal/mol. This was attributed to the formation of the "twist boat" conformation of the 6 member ring as mentioned previously. To reduce this energy, the ring was manipulated to a chair conformation and the MM2 re-run. This reduced the total energy to 53.1737 kcal/mol mainly due to bend and 1,4 dipole energy improvements. To improve the energy further, manipulation of the 10 member ring via invertig some of the carbons resulted in a total energy of 44.2941 kcal/mol. Additionally the carbonyl was optimised pointing further down than the higher energy down-atropisomers, with a sp² bond angle of 120°.

Discussion

Clearly the carbonyl orientation in these atropisomers has a large effect on the total energy of them, and thus one is more stable than the other. MM2 calculations have indicated that the most stable is when the carbonyl points down with an energy of 44.2941 kcal/mol versus the structure with the carbonyl up at 48.8841 kcal/mol, a (9.3% difference).

It is also noted that the alkene in this compound is unusually hard to functionalise, essentially the alkene function is more stable than would be expected. One would expect the alkene to readily react due to the bridge-head directly adjacent causing stain at the sp² centre (The angle at the sp² carbon next to the bridge head is 108°)

The angle at the carbon adjacent to the bridgehead is shown. Note, hydrogens removed for clarity

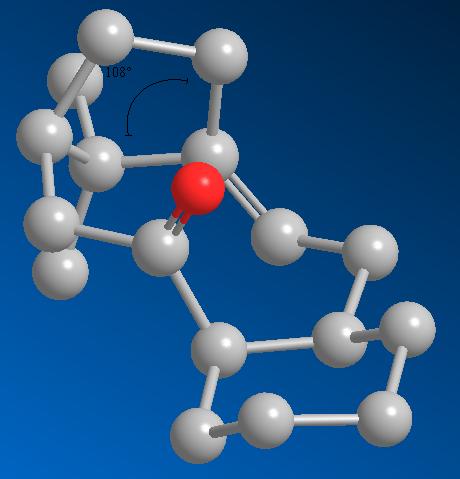
The best way to approach explaining this anomaly is to model the resulting alkane from functionalising the alkene and compare energies, the simplest option is to add hydrogens across the alkene. The lowest energy atropisomer (shown above) was used with a total energy of 44.2941 kcal/mol. The double bond was changed to a single bond and the MM2 minimisation was run.

Potential Function	Alkane	Down Chair Conformation + 10C adjustment	Difference
Stretch	3.006	10.6331	-7.6271
Bend	14.9416	0.3117	14.6299
Stretch-Bend	0.5809	19.7852	-19.2043
Torsion	21.6112	-1.3707	22.9819
Non-1,4 VDW	-1.0187		-1.0187
1,4 VDW	15.2641	12.5613	2.7028
Dipole/Dipole	0	-0.1812	0.1812
Total Energy (kcal/mol)	54.3851	44.2941	10.091

The result is an increase in energy from 44.2941 kcal/mol to 54.3851 kcal/mol thus this is not a thermodynamically favourable process. In more detail, the main contributing energies were bend and torsion energy increases, implying that the cyclic alkene actually reduces the torsional and bend strain of the molecule. Considering the bond angles at sp² (120°) versus sp³ centres (109°), the tighter angle of the sp³ may induce more bending and torsional strain in larger ring sizes than the more obtuse sp² angle. This would explain the disfavour in losing the sp² hybridisation in the 10-carbon ring. A decagon has internal angles of 144°, slightly larger than a sp² centre, obviously tightening (making it more acute) the angle to 109° would be disfavoured.

How one might induce room temperature hydrolysis of a peptide

This experiment looks at the rate of hydrolysis of peptide bonds in mild conditions. 2 different molecules are investigated where the rate of hydrolysis is very different (reaction scheme below). Each precursor has 2 possible isomers (where the group of the ring nitrogen is axial or equatorial), these are modeled first to find the lowest energy conformation and thus the predominant isomer. These are then analysed and the reason for such a large difference in rates determined.

Peptide hydrolysis reaction scheme

Precursor 1 (13)

This molecule is based on a cis-decalin ring system, which can undergo ring-flipping although this is ignored in this precursor, it is mentioned because trans-decalin based systems (precursor 2) cannot. The two isomers were modelled in ChemBio3D and optimised by MM2 minimisation.

Isomers of Precursor 1

Equatorial isomer	Axial isomer
Equatorial	Axial

Equatorial -OH

Potential Function	Conformation 1	Conformation 2	Conformation 3	Conformation 4	Conformation 5
Stretch	1.7639	1.7523	1.7081	1.7984	1.641
Bend	4.7224	5.0282	4.6863	6.3095	5.3668
Stretch-Bend	0.5257	0.528	0.5143	0.5934	0.566
Torsion	7.8225	8.2145	7.6811	7.7579	8.4941
Non-1,4 VDW	-3.4285	-2.2815	-3.1854	-5.4231	-6.0518
1,4 VDW	9.7609	9.5586	9.697	9.2192	9.5645
Dipole/Dipole	-3.295	-2.2691	-3.9469	-4.8783	-6.1394
Total Energy (kcal/mol)	17.872	20.531	17.1544	15.3769	13.4412

The first minimisation after the molecule was drawn gave a total energy of 17.872 kcal/mol, inverting the positions of the carbonyl and amine group on the equatorial position gave an increase in energy to 20.531 kcal/mol. Rotation of the -OH proton on the original molecule away from the other substituents resulted in a decrease in energy to 17.154 kcal/mol. The α-carbon of the carbonyl was moved above the plane of the ring which when minimised, reduced the total energy to 15.3769 kcal/mol. Upon flipping the carbonyl towards the -OH proton (trying to achieve H-bonding) the energy of the conformer dropped considerably to 13.4412 kcal/mol.

Axial -OH

The ring flipping allows the -OH group to change between axial and equatorial in this molecule. Thus even though the reaction scheme shows the -OH equatorial, it must also be considered in the axial position.

Potential Function	Conformation 1
Stretch	1.5938
Bend	4.2454
Stretch-Bend	0.576
Torsion	8.006
Non-1,4 VDW	-2.8568
1,4 VDW	9.3001
Dipole/Dipole	-2.9733
Total Energy (kcal/mol)	17.8912

The molecule was drawn and minimised, this time the starting conformation was drawn to achieve the best H-bonding resulting in a total energy after minimisation of 17.8912 kcal/mol. This is a higher energy than when the -OH was equatorial, looking at the dipole/dipole energies (H-Bonding) the energy stabilisation from H-Bonding is much less in the axial -OH case (the -OH proton and carbonyl are a further distance apart) than the equatorial -OH conformer.

Equatorial -OH

Potential Function	Conformer 1	Conformer 2	Conformer 3	Conformer 4
Stretch	1.655	1.5536	2.3348	1.444
Bend	8.0779	7.8561	108.1818	7.8566
Stretch-Bend	0.6738	0.635	0.1588	0.5983
Torsion	10.4181	11.2328	11.7521	11.5289
Non-1,4 VDW	-2.7007	-5.0774	-6.7675	-8.1756
1,4 VDW	9.5423	10.0119	11.5844	10.4332
Dipole/Dipole	-1.4314	-3.0433	-4.9858	-4.3884
Total Energy (kcal/mol)	26.235	23.1686	122.2587	19.297

The MM2 was run and the total energy was found to be 26.235 kcal/mol, the -OH hydrogen was then rotated towards the carbonyl to try and achieve some H-bonding, this led to an energy reduction of 3.0664 kcal/mol to 23.16 kcal/mol. The carbonyl α-carbon was rotated towards the -OH proton to get H-bonding, but this led to massive steric interactions and a huge leap in bending energy (108 kcal/mol). On further investigation, the carbonyl carbons sp² bond angle was 173° - a huge bending strain. The previous minimum energy molecule was loaded and the carbonyl and amine group inverted so that the smaller carbonyl was pointing towards the ring hydrogens (sterics). This gave the lowest energy geometry at 19.297 kcal/mol.

Axial -OH

Potential Function	Conformer 1
Stretch	1.5565
Bend	12.3738
Stretch-Bend	0.8121
Torsion	12.1467
Non-1,4 VDW	-2.7398
1,4 VDW	9.7122
Dipole/Dipole	-3.0147
Total Energy (kcal/mol)	30.8468

The -OH and peptide groups were both manipulated to the axial positions and the MM2 was run, giving a total energy of 30.8468 kcal/mol. This was not improved upon because there is no possible H-bonding because the groups are on opposite faces.

Comparison of results

Potential Function	Eq pep, Eq -OH	Eq pep, Ax -OH	Ax pep, Eq -OH	Ax pep, Ax -OH
Stretch	1.641	1.5913	1.444	1.5565
Bend	5.3668	4.2477	7.8566	12.3738
Stretch-Bend	0.566	0.5759	0.5983	0.8121
Torsion	8.4941	8.006	11.5289	12.1467
Non-1,4 VDW	-6.0518	-2.8573	-8.1756	-2.7398
1,4 VDW	9.5645	9.3	10.4332	9.7122
Dipole/Dipole	-6.1394	-2.9725	-4.3884	-3.0147
Total Energy (kcal/mol)	13.4412	17.891	19.297	30.8468

From these results it is clear that the most thermodynamically favoured isomer is when the peptide is equatorial and the -OH group is equatorial. This can be explained by the H-bonding between carbonyl and alcohol functions. H-bonding is a favourable interaction which lowers the total energy (by showing more negative values of Dipole/Dipole energies) It is directly related to the distance of the interacting dipoles and thus when they are closest, the stabilisation is best. When both substituents are equatorial they dipoles are closest and thus the stabilisation is best. The energy difference between peptide orientations when the -OH is axial is 5.8558 kcal/mol, this is in close agreement with the literature value of 5.1 kcal/mol.

Precursor 2 (14)

Unlike precursor 1 the cis decalin structure allowed ring flipping to occur, this is no longer the case in a trans decalin structure where ring flipping is prohibited by the torsional strain in the product.

Isomers of Precursor 2

Equatorial isomer	Axial isomer
Equatorial	Axial

Equatorial peptide

Potential Function	Conformer 1	Conformer 2
Stretch	1.6039	1.5576
Bend	3.5854	3.2811
Stretch-Bend	0.514	0.4908
Torsion	7.4426	7.2332
Non-1,4 VDW	-6.3134	-8.1521
1,4 VDW	9.8124	9.8295
Dipole/Dipole	-4.9334	-5.2114
Total Energy (kcal/mol)	11.7114	9.0286

The structure was drawn and MM2 optimised to find an inital total energy of 11.7114 kcal/mol. Significant H-bonding was established between the -OH group and the NH₂ lone pair. The NHsub>2 and C=O were then inverted on the α carbon so that the carbonyl was closer to the -OH, the proton on the -OH was rotated towards the carbonyl to establish if the H-bonding between these 2 groups is more stabilising than previously. After MM2 minimisation a total energy of 9.0286 kcal/mol was obtained. Other atoms were then moved slightly and the geometry optimised, but with no real reduction in total energy.

It is clear between these 2 conformers that the Dipole/Dipole and Non-1,4 Van der Waals energies are the main contributors to stabilisation of conformer 2 over conformer 1. These can then be translated to H-bond stabilisation, in effect conformer 2 H-bonding is much more stabilising.

Axial peptide

Potential Function	Conformer 1	Conformer 2
Stretch	1.6904	1.5543
Bend	5.5029	5.1158
Stretch-Bend	0.6071	0.553
Torsion	8.6997	8.6601
Non-1,4 VDW	-5.0294	-7.0053
1,4 VDW	9.5103	9.6052
Dipole/Dipole	-6.8234	-6.4202
Total Energy (kcal/mol)	14.1577	12.0629

The peptide group was moved into the axial position and an inital MM2 minimisation run, the total energy was 14.1577 kcal/mol. When compared to the equatorial energies, bend energy was increased, but so was the H-bonding stabilisation. The sp² centre of the carbonyl was at 114° bond angle, and this strain rationalised to achieve better H-bonding interactions. The carbonyl was twisted manually to the NH₂ position and MM2 re-run, the resulting energy was 12.0629 kcal/mol (14.7% improvement) with a bond angle of 115°.

Comparison of Results

Potential Function	Equatorial	Axial
Stretch	1.5576	1.5543
Bend	3.2811	5.1158
Stretch-Bend	0.4908	0.553
Torsion	7.2332	8.6601
Non-1,4 VDW	-8.1521	-7.0053
1,4 VDW	9.8295	9.6052
Dipole/Dipole	-5.2114	-6.4202
Total Energy (kcal/mol)	9.0286	12.0629

Clearly the conformation where the peptide group is equatorial is the thermodynamically most favourable (an energy difference of 3.0343 kcal/mol), this is in agreement with the literature value of 3.1 kcal/mol. Although the axial isomer has better Dipole/Dipole or H-bonding stabilisation (1.2088 kcal/mol extra stabilisation), it has an increased bend energy (1.8347 kcal/mol more unstable) and increased torsion energy (1.4269 kcal/mol more unstable). The trans decalin structure has prevented ring flipping in this case so different orientations of the -OH were not considered.

Discussion of Results

The starting compounds have been investigated and the most thermodynamically stable isomer identified in each equilibrium case (with results that are in close agreement with literature values), reactivity of the starting materials now must be considered. There are a number of factors that come into question:

• Proximity of reacting functions in the isomers
• Angle of attack at the carbonyl (Burgi-Dunitz)
• Whether the thermodynamically most stable isomer is the reacting conformer (Curtin-Hammet principle)
• Energies of the intermediates

Data on distances from the oxygen on -OH to the carbonyl were collected because the probability of intramolecular reaction increases with decreasing distance between reacting functions. A finer point to consider is the required angle of attack on the carbonyl, since this is a nucleophilic attack the -OH oxygen attacks the LUMO at the carbonyl function, if we consider localised orbitals instead of MOs the LUMO becomes the C=O π^*. This orbital points away from the C=O bond at an angle of 107° which then directly influences the angle of nucleophilic attack to 107° above or below the plane of the C=O, this was first published by H. B. Bürgi and J. D. Dunitz hence the popular name the "Burgi-Dunitz" angle. With this in consideration, the requirement for this angle of attack was investigated and correlated with the distance of reacting functions.

	Energy kcal/mol	Distance (Å)	Angle (°)	Deviation from Burgi Dunitz (°)
13 Axial	19.2947	3.6	178.4	71.4
13 Equatorial	13.3946	3.1	169.7	62.7
14 Axial	12.0064	2.9	51	56
14 Equatorial	9.0282	3.1	65	42

This data shows that in precursor 1, the equatorial-ethylamido isomer is the most stable thermodynamically, has a smaller distance between reaction moeities and also the least deviation from the required Burgi-Dunitz angle (since approach by the nucleophile must be on this angle, it is assumed the closer the oxygen is to the 107°, the less energy is required to move it onto that angle). This rationale supports the reference in that the most stable conformation is the reacting conformation.

The journal reference cited for this experiment states that "the ethylamido group can undergo intramolecular nucleophilic attack by the 8-hydroxyl group only in 4[Precursor 1]. In derivative 5[Precursor 2], the ethylamido group must first, at an energetic cost, invert to the axial position." It appears that the authors have not considered rotating the ethylamido group round the α-carbon, giving a perfectly reasonable attack angle and distance. In fact when modelling this molecule using MM2, the most stable configuration was that with the carbonyl facing the opposite way to that drawn in the reference (allows H-bonding to occur).

The most stable orientation of the ethylamido group in precursor 2

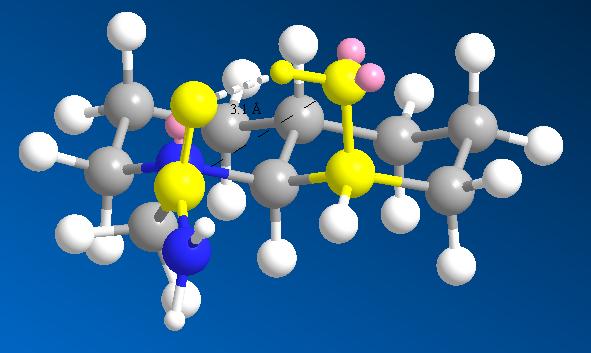
Precursor 2 has the equatorial ethylamido isomer as its lowest energy conformer also, but here the distance of reacting functions is further in this conformation than in the axial case. The difference between the different isomers is 0.2Å (6.4%) which is easily overcome by thermal vibrations at room temperature. Comparing the deviation from optimum attack trajectory, the equatorial has a closer fit than the axial case (the reference suggests otherwise), thus the explanation for such different rates between 13 and 14 is unlikely to be as the reference suggests (that the equatorial ethylamido isomer requires inversion to its higher energy isomer before reacting).

For a better insight into the reason for the difference in rates, the first intermediate was modelled in each case giving intermediate energies:

Potential Function	13EQ	13AX	14EQ	14AX
Stretch	1.4692	1.2873	1.4083	1.351
Bend	5.0397	6.9005	4.0495	4.0017
Stretch-Bend	0.4347	0.5433	0.5225	0.5139
Torsion	13.2915	13.1151	9.0566	9.0551
Non-1,4 VDW	-5.8191	-4.1309	-3.6382	-3.6425
1,4 VDW	15.0697	11.8703	11.8518	12.0078
Charge/Charge	0	0	0	0
Charge/Dipole	-1.0866	2.2558	2.337	2.2253
Dipole/Dipole	4.2294	3.2177	4.4237	3.7551
Total Energy (kcal/mol)	32.6285	35.059	30.0112	29.2673

These support the argument for precursor 1, the intermediate formed when the equatorial isomer is attacked is lower in energy than the axial case (2.4305 kcal/mol). For precursor 2, the intermediate formed from the axial isomer is slightly lower in energy than the equatorial case. This could be a reason why precursor 2 reacts from its axial isomer. A closer look via modelling transition states to the intermediate may give some insight to the kinetics of the argument which may explain why precursor 2 reacts from its less stable isomer (allowed by the Curtin-Hammett principle, stating that it does not have to be the most thermodynamically stable reactant that reacts to form the major product, a good discussion can be found here). There are many factors not modelled in MM2 which could explain the reason for this behavior, understanding the electronics (molecular orbitals) may give a better kinetic understanding of the reaction and thus provide an answer (although there is no time for this now). Modelling of the transition states (not possible in MM2) would give the best approximation for kinetic variations of precursors.

Modelling Using Semi-empirical Molecular Orbital Theory

Part 1

Semi-empirical molecular orbital theory is a more advanced technique used to model molecules compared to the MM models used previously. This theory can be thought of as a step between pure Newtonian mechanics methods which do not consider electronics and pure quantum mechanical theory where the hamiltonian is calculated explicitly. Semi-empirical methods (as the name suggests) calculates the molecular orbitals of a molecule, but uses empirical forms and energies of the constituent atomic orbitals. The minimum energy of an orbital is calculated using a self-consistent field (where the solution behaves as if each particle is influenced by the net field of all other particles in the system). Various methods of calculation are used depending on the form and number of integrals used to define the atomic orbital. These methods include the complete neglect of differential overlap (CNDO), the intermediate neglect of differential overlap (INDO) and the neglect of diatomic differental overlap (NDDO).

Diene molecule being investigated via MM2, PM3, HF/STO-3G and B3LYP/6-31G(d) methods

PM3

The molecule was MM2 optimised to 17.9051 kcal/mol in ChemBio3D, saved as a .gjf and loaded in Gaussview to run a Semi-empirical PM3 job which took roughly 1min to run at 500mb memory usage on the laptop. The .chk file was retrieved and the HOMO and LUMO visualised:

HOMO	LUMO

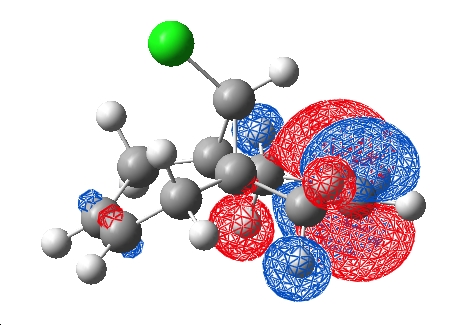
HF/STO-3G

As a comparison, a HF/STO-3G was submitted to scan (pool 1) using a word pad and job code "# opt hf/sto-3g" along with the title and cartesian coordinates, this ran with 3.6Gb allocated memory in 10mins. The checkpoint and log files were retrieved and the .chk visualised in Gaussview, the HOMO and LUMO:

HOMO	LUMO

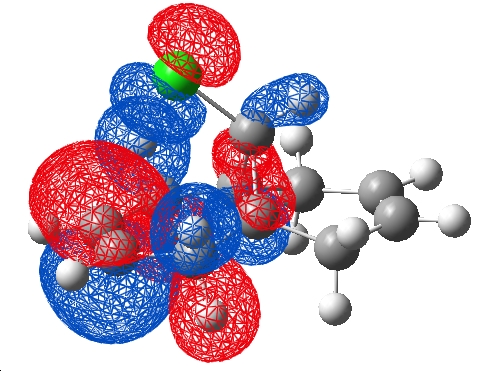B3LYP/6-31G(d)

A Density function theory (DFT) B3LYP/6-31G(d) calculation was submitted to scan (pool 1) using the HF/STO-3G optimised coordinates but with command line "# opt b3lyp/6-31g(d)" and a title, the .chk was retrieved 25mins later, the HOMO and LUMO were visualised in Gaussview:

HOMO	LUMO

Comparison

The geometries of the optimised molecule varied very much between levels of calculation this is shown in the comparison below:

MM2	PM3	HF/STO-3G	B3LYP/6-31G(d)

In addition the angle of the C-Cl bond to the plane of the 3 member ring was measured in each case, the calculation times taken to achieve each result were also tabulated for interest:

Calculation type	Angle of C-Cl bond to the 3 member ring	Exo distance to bridge C (Å)	Eno distance to bridge C (Å)	Time to complete (mins)
MM2	107.5	2.967	3.218	<0.5
PM3	109.4	3.042	3.451	<1
HF/STO-3G	111.6	3.019	3.236	10
B3LYP/6-31G(d)	112.2	3.019	3.236	25

As calculation level increased, the C-Cl angle increased too but in increasingly small amounts. The time taken for each of these calculations to run increases with complexity of the calculation, thus there is a trade off for refinement of the calculation with the time it takes to run. Interestingly the MM2 model looks more similar to the DFT version than the PM3! Although the C-Cl angles are very different, the ring in both cases is very flat compared with the other models.

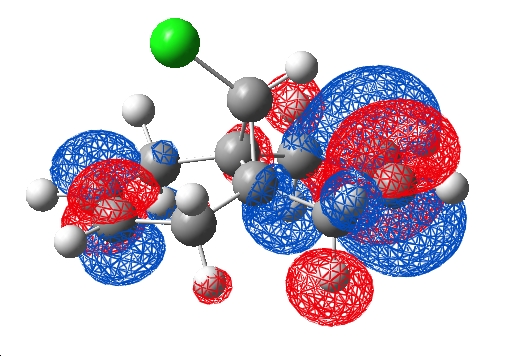
Another interesting aspect of the differences in these models is an electronical difference between semi-empirical PM3 and the other 2 quantum mechanical models. The HOMO predicted by PM3 has some electron density based on the alkene which the chlorine is not facing, whereas the other 2 models have no density based here. With respect to the LUMO, as calculation level increases the LUMO becomes more evenly distributed across the molecule. Finally, the PM3 differs again in the way the phases of the HOMO and LUMO orientate, the HOMO on the chlorine and top side of the alkene are the same phase in the PM3 case and opposite phases in the other quantum models. This may be because PM3 does not start from first principles like the HF and DFT models.

Part 2

The diene and dhydrogenated form were modelled, MM2 optimised and the submitted with the command line "# opt freq b3lyp/6-31g(d)". These were recovered and the relevant stretching frequencies identified.

Stretch	Diene (cm-1)	monohydrogenated alkene (cm-1)
C-Cl	772.634	776.58
C=C (exo)	1740.76	N/A
C=C (endo)	1760.91	1761.67

Clearly upon hydrogenation of the exo alkene the C-Cl bond increases in strength (3cm^-1 in IR frequency). Additionally noted was the differnece in exo vs endo double bond strength (exo was 20cm^-1 weaker than the the endo ene function). From a PM3 orbital perspective this can be explained by an in-phase proximity of the C-Cl σ^* and exo double bond π orbital, this allows donation of electron density from the alkene to the C-Cl σ^* thus destabilising the C-Cl bond (occupation of the antibonding σ^* is destabilising). When this effect is removed via hydrogenation of the exo double bond, the C-Cl bond becomes stronger (illustrated by a upwards shift in the IR frequency (cm^-1)).

When the DFT orbitals were considered, as mentioned earlier, it was noticed that the orbitals were of polarised symmetry. The LUMO +2 and HOMO -1 were visualised and a nodal plane were the previous interaction was discussed. This negates the interaction of the exo п orbital with the C-Cl σ^* in this case leaving the changes in C-Cl strength (which still occur in a DFT frequency calculation) unrationalised.

The HOMO -1 and the LUMO +2 visualised	The HOMO -1 and the LUMO +2 visualised
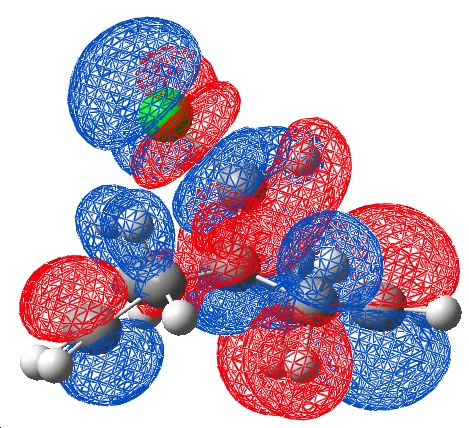DFT	PM3

AIM Analysis

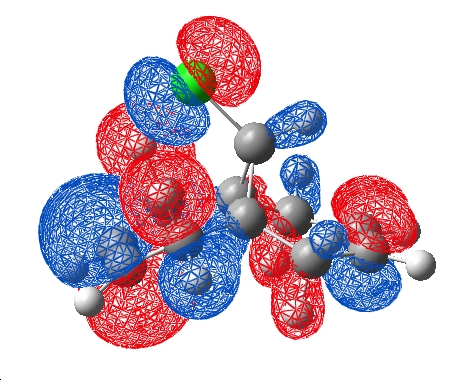
Due to this major difference in the two models, an AIM topological calculation was run on the model in an attempt to find the true electronic density locations in the molecule. This was visualised:

AIM topological view of the dinene molecule

This calculation calculates the 2^nd derivative of the electron density with respect to 3D cartesian coordinates, using a 3x3 matrix and applying the Laplace (Δ) operator.

Where f is a function that is real when differentiated twice:

Eigenvalues are extracted which can be positive or negative in each of the 3 dimensions. The curvature of the electron density at a particular point has certain characteristics which AIM can evaluate, for example when the the eigenvalues are all positive, a red point is placed. Rings can be identified by a yellow point in their centre and cages by the green points. Interestingly, a red point appears between the chlorine atom and the centre of the endo double bond. This indicates a bonding interaction between the chlorine and the electron density formally described as the endo double bond. This interaction was on the order of a hydrogen bond in terms of electron density. It was also noted that no points occur between the carbon of the C-Cl bond and the middle of the exo double bond. This does not nessecarily mean there is no interaction here, but that the electron density does not have the specific curveture that is required for formal identification as a bond.

The bonding interaction identified by the topological calculation suggests that the endo π orbital on the chlorine face and the chlorine suggest that there must be some constructive overlap here which is not obvious in the DFT model (although there is a in phase possibility of the LUMO +2 centred on the chlorine and HOMO on the endo alkene)

The HOMO and LUMO +2 from DFT optimisation (iso = 0.005)

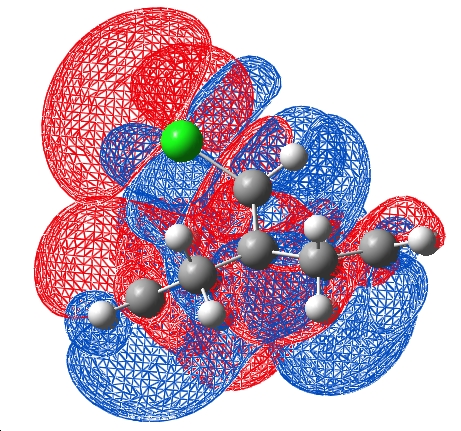
The HOMO of the endo double bond potentially could overlap with the σ^* of the C-Cl, inducing the lengthening of the double bond

Structure based Mini project using DFT-based Molecular orbital methods

Introduction

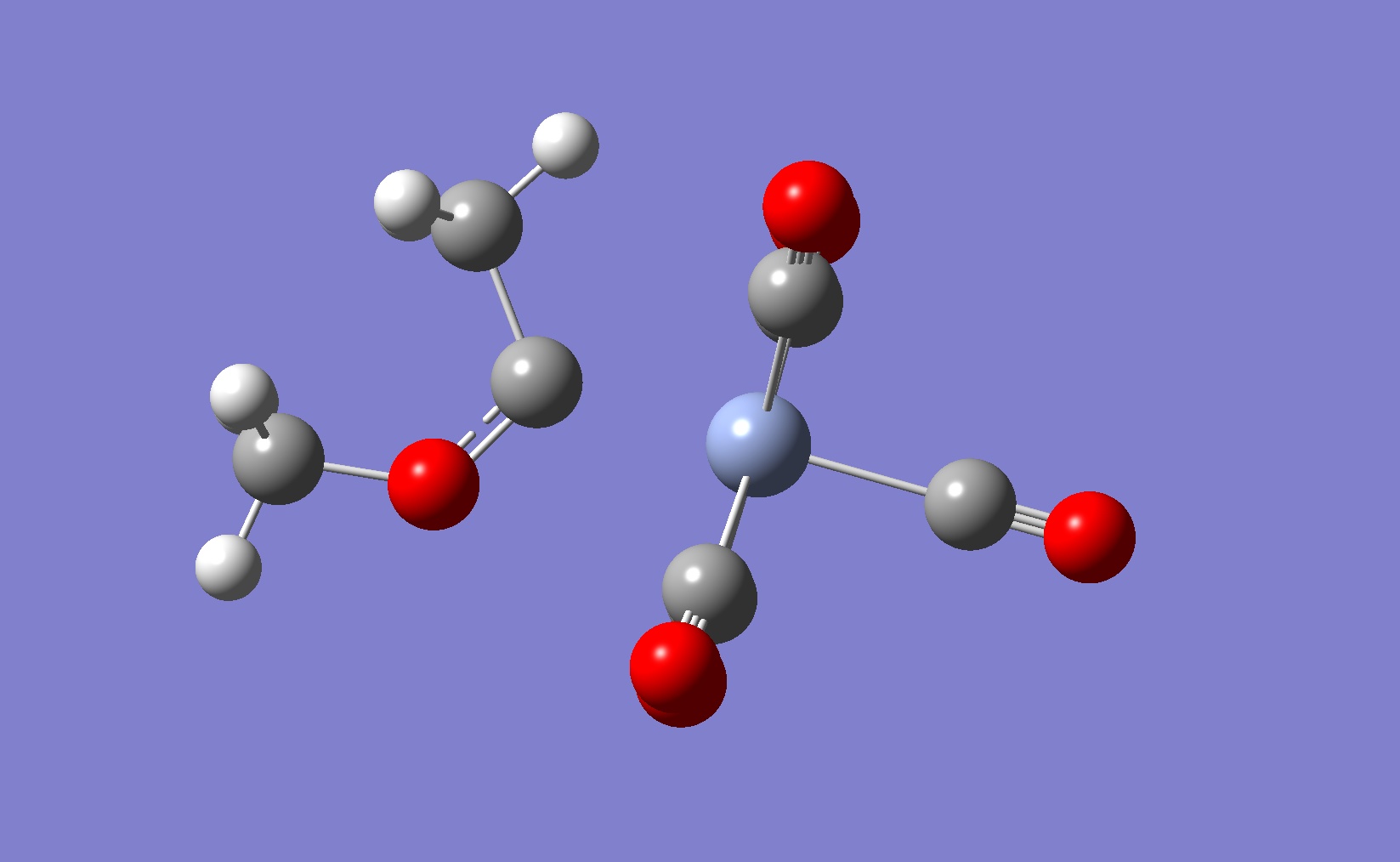
This experiment uses computational techniques to investigate a recently (2009) published metal catalysed [2+2+2] intermolecular cycloaddition reaction. Metal catalysis of intermolecular cycloaddition reactions involving a terminal alkyne and an alkene has potential to become a very popular method for synthesising substituted cyclo 1,3-dienes, the difficulty being controlling regio and stereo chemistry in the product. An extensive investigation of this cycloaddition reaction between tert-Butylacetylene (1) and 1-hexene (2) was carried out by Y. Obora et al using Nb(III) catalysts.

Reaction scheme modified from the publication

2 major 1,3-diene product compounds were observed follwing the 4h reaction, along with a small mixture of a tri-substituted aromatic compounds:

• 1,4-di-tert-butyl-5-butyl-1,3-cyclohexadiene (3)
• 1,3-di-tert-butyl-5-butyl-1,3-cyclohexadiene (4)
• tri-tert-butylbenzenes (5)

The group then went on to characterise the products using ¹H and ¹³C NMR, assigning resonances using a variety of techniques including 2D HMQC, HMBC and NOESY spectroscopy. The aim of this experiment is to compare computational NMR predictions with the groups extensive characterisation.

Methods

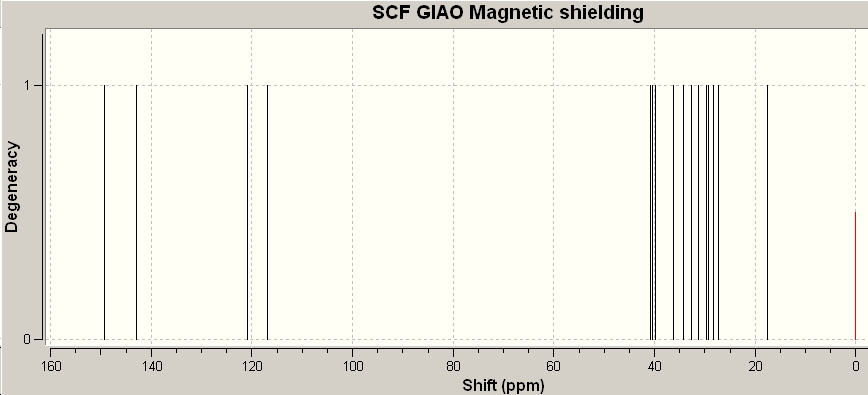
The NMR predictions will be made by optimising the structure using DFT methods, then using the Gague Invarient Atomic Orbital (GIAO) method to predict 1H and 13C NMR spectra. Very simplistically, this method introduces a magnetic field in the form of a vector potential from a guage origin and calculates the pertubation of the wavefunction by this field ie. the electronic Hamilton operator is expanded to include the external magnetic field and the magnetic field of the nuclear magnetic moments. Knowing that the magnetic shielding is the second order derivative of molecular energy with respect to the external magnetic field then allows the magnetic shielding to be calculated and thus the chemical shift prediction to be made. An excellent, more detailed discussion can be found here.

Optimisation was performed using DFT B3YLP and a 6-31G basis set. Previously minimised structures (via Hartree Fock methods with STO-G basis sets) were submitted for the DFT optimisation. These optimised structures were then submitted for GIAO NMR calculations with the commandline "# mpw1pw91/6-31(d,p) NMR scrf(cpcm,solvent=chloroform)"

Results

• Molecule 3 - DOI:10042/to-1616
• Molecule 4 - DOI:10042/to-1617
• Molecule 5a - DOI:10042/to-1618
• Molecule 5b - DOI:10042/to-1619
• Molecule 5c - DOI:10042/to-1620

Since the paper does not give spectra for the 5x compounds, molceules 3 and 4 GIAO and published spectra are going to be focused on.

Molecule 3

The NMR shifts as reported by Y. Obora et al.

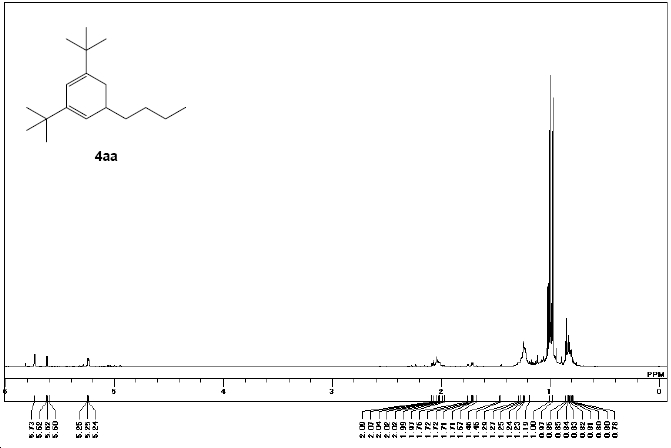
δH (270 MHz; CDCl3, Me4Si) 0.87 (t, 3J(H,H)= 7 Hz, 3H), 1.05 (s, 9 H), 1.09 (s, 9H), 1.12‐1.36 (m, 4H), 1.49‐1.59 (m, 2H), 2.04‐2.12 (m, 2H), 2.31 (d, 3J(H,H)= 15 Hz, 1H) and 5.69 (s, 2H)

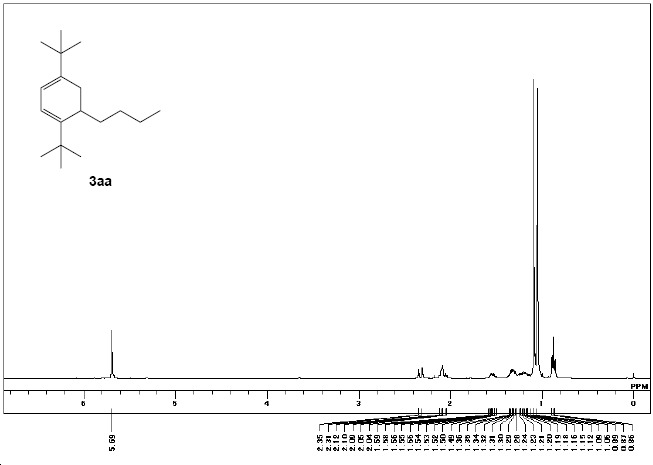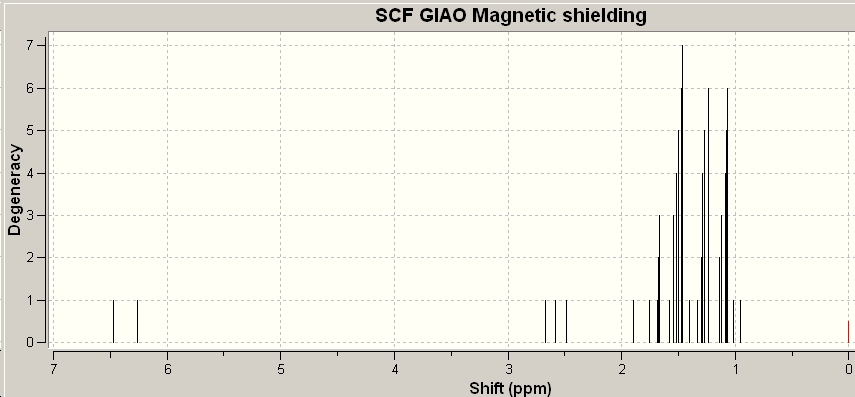
Experimental 1H NMR	GIAO calculated NMR

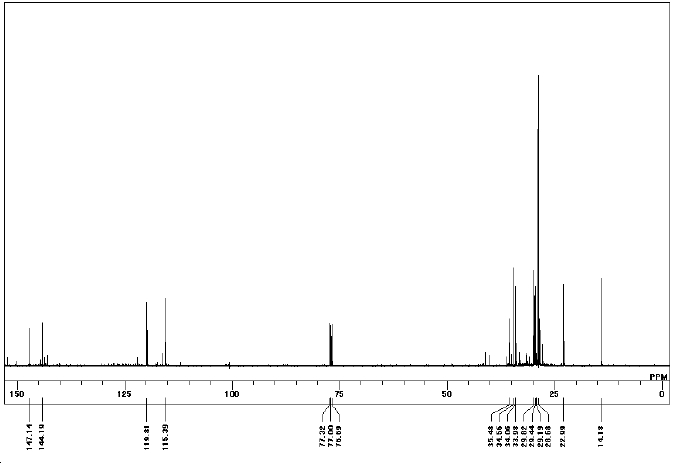
δC (67.5 MHz; CDCl3, Me4Si) 14.2 (CH3), 22.8 (CH2), 27.8 (CH2), 28.2 (CH2), 28.5 (3C, CH3), 29.6 (3C, CH3), 29.8 (CH2), 33.2 (CH), 35.0 (C), 35.6 (C), 115.4 (CH), 115.5 (CH), 143.6 (C) and 150.3 (C)

Experimental 1H NMR	GIAO calculated NMR

Molecule 4

δH (270 MHz; CDCl3, Me4Si) 0.78‐0.85 (m, 3H), 0.97 (s, 9H), 1.00 (s, 9H), 1.19 ‐1.46 (m, 6H), 1.67‐1.76 (m, 1H), 1.97‐2.09 (m, 2H), 5.24‐5.25 (m, 1H) and 5.60 ‐5.73 (m, 1H)

Experimental 1H NMR	GIAO calculated NMR

δC (67.5 MHz; CDCl3, Me4Si) 14.2 (CH3), 23.0 (CH2), 28.7 (3C, CH3), 29.2 (3C, CH3), 29.4 (CH2), 29.8 (CH2), 34.0 (CH3), 34.1 (CH2), 34.6 (CH), 35.5 (C), 115.4 (CH), 119.8 (CH), 144.2 (C) and 147.1 (C)

Experimental 1C NMR	GIAO calculated NMR

Discussion

To compare the experimental NMR data to the GIAO prediction, the signals were tabulated and then plotted against each other:

Molecule 3

Molecule 4

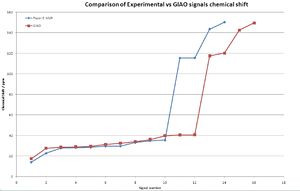
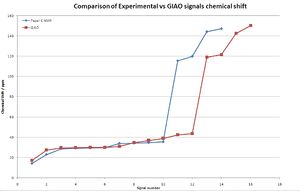
It is clear that the overall fit is very good, the shift of the GIAO method is due to the overlap of signals in the experimental spectrum leading to fewer signals being present. An application of this NMR method is to check if the NMR assignment is correct, ie the corect isomer is isolated. To investigate this the data was again tabulated and compared graphically:

Comparison of chemical shifts

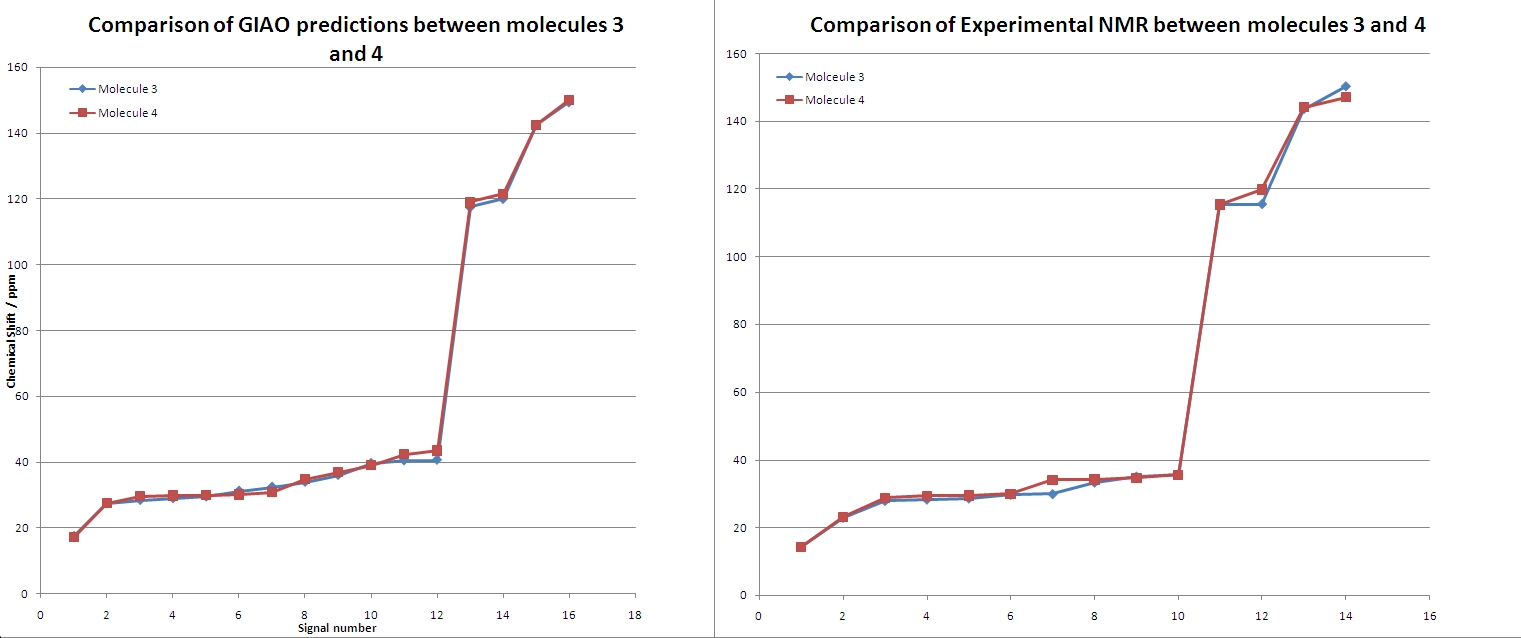
Clearly from this comparison, the experimental and GIAO method agree. Although there is some fluctuation in the signal patterns. The distiguishing features in the predicted NMR are:

• Molecule 4s signals 2 - 5 are slightly higher shifts than molecule 3
• A dip at signal 7 where molecule 4 has a lower shift signal than molecule 3
• Signal 12 is higher in molecule 4 than 3
• Signals 13 and 14 from molecule 4s spectrum are slightly higher than molecule 3

Transfering these patterns to the observed signals shows a good correlation of the patterns. The pattern at signal 13/14 is present and very clearly in agreement with the experimental values. The increase at 12 was not observed in experimental results, nor was the dip at signal 7. Although this coud be due to a different number of signals between experimental and GIAO method causing a shift of the dip. Signals 2-5 showed a good agreement in the shift patterns.

This analysis has concluded that the experimental analysis was correct and that the NMR of each isomer was of the intended molecule. Despite molecules 3 and 4 being isomers of each other, a slight difference in chemical shift between the two enabled them to become distiguishable by NMR. When comparing the GIAO prediction with the experimental values, a firm agreement was noted, but also some deviations between the two signal patterns.