Rep:Mod:AlphabetMinestrone
Modelling Using Molecular Mechanics
Module 1
The Hydrogenation of a Cyclopentadiene Dimer
Cyclopentadiene slowly undergoes dimerisation with itself, in a Diels-Alder process at room temperature. The Diels-Alder reaction can occur with the cyclopentadiene rings in two different arrangements - resulting in two separate products - an exo and an endo. This reaction can be either kinetically or thermodynamically controlled, depending on reaction conditions. The thermodynamic product is the product that has the lowest total energy, whilst the kinetic product is the product with the lowest activation barrier. There would never be just one product within our final stages of the reaction, as the dimer will be in equilibrium with the other viable product, and the reactant. We are told that the procedure results in the endo dimer and as such we expect the kinetics to rule the composition of our product, so the reaction is dependent on the best overlap of the HOMO of the dienophile and the LUMO of the diene. Using molecular modelling, I aimed to see if the relative energies of the two products support this theory.
 |
 |
 |
 |
| Parameter | Energy (10-3 Eh) | |||
|---|---|---|---|---|
| Structure | Exo Dimer | Endo Dimer | Structure 3 | Structure 4 |
| Stretch | 2.042 | 2.011 | 2.030 | 1.749 |
| Bend | 32.780 | 33.255 | 31.695 | 23.159 |
| Stretch-Bend | -1.334 | -1.329 | -1.334 | -0.868 |
| Torsion | 12.219 | 15.139 | 17.173 | 19.933 |
| Non-1,4 VDW | -2.256 | -2.415 | -1.957 | -1.674 |
| 1,4 VDW | 6.750 | 6.839 | 9.003 | 7.173 |
| Dipole/Dipole | 0.602 | 0.709 | 0.258 | 0.224 |
| Total Energy | 50.803 | 54.209 | 56.870 | 49.696 |
Above, you can see four molecules: structure 1, where the dimer is from the exo reaction, structure 2 where the dimer is from the endo reaction, and structures 3 and 4, the two possible hydrogenated products of structure 2.
From the data calculated by the MM2 forcefield in ChemBio3D (left) we can see immediately, that actually the exo product was thermodynamically favoured, having the lowest conformational energy of the two. From the data we can also see that the factor that caused this shift from endo to exo was the increased torsional energy in the endo product that was lower in the exo structure. This torsional strain arises from the steric interactions between the bridge within the 6-membered ring and the 5-membered ring, and thus the dimerization of cyclopentadiene is kinetically controlled - due to the low energy of the endo transition state.
The hydrogenation of this dimer (via a Lindlar catalyst, and hydrogen) can gives us two products that we wish to understand. The double bond within the 5-membered ring (different from the 6-membered ring with a bridge) is unstable (structure 3), and the hydrogenation of this double bond therefore removes any stability brought about by it, and makes the hydrogenation slightly unfavourable. On the other hand, the hydrogenation of the unsaturated 6-membered ring (structure 4) is favoured greatly, and as you can see from the data, this hydrogenation greatly decreases the energy from bending, more than the associated increased torsional energy. As such, we'd expect to see structure 4 as our major product in this hydrogenation, assuming that complete hydrogenation does not occur.
Stereochemistry of Nucleophilic additions
Molecule 5
 |
 |
 |
 |
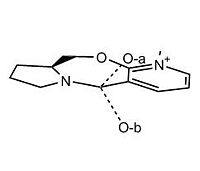
The alkylation of molecules containing pyridinium rings readily occurs, and is a common and useful reaction within the pharmaceuticals industry. For the molecule above, we are looking at the conformations available, and how they can react with an alykylating agent, such as Grignard reagents or other organometallic reagents (organolithium/cuprate), which are highly stero- and regio-selective. The alkylation can occur at either the 4 or 6 positions, and we're told the alkylation occurs at the 4 position, and so it must be the predominant attack site. The attack site is dictated by the sterics of the molecule - bulkier nucleophiles can only attack those positions that are less hindered. Upon applying the MMFF94 forcefield to the newly created molecule, we can obtain a basic energy value for this molecule. Due to the planar nature of the body of this molecule, and the avail twisting modes of joined rings, there was likely to be a difference between conformations beneath and above the plane. To test this, I decided to minimize the energy of this structure, from two locations - one where the oxygen atom of the carbonyl is above the plane, and once where it is beneath the plane (O-a and O-b, respectively). However, upon minimizing the energy from both positions, the forcefield arranged the atoms in identical positions, giving the same minimized energy values to 0.01 Hartrees. With such a strong tendancy to be above the plane of the molecule, we can hypothesise that the carbonyl will always be above the plane of the molecule, albeit possibly with a varying degree from 0 to ~35o, but will never be beneath and stable.
It is possible for us to obtain two conformers of this moelcule - depending on the structure of the 5-membered ring. The carbon and the nitrogen atoms shared by the both the 5 and 7-membered rings are almost planar to their adjacent carbons within the 5-membered ring, leaving the carbon atom 2 away from the shared nitrogen and carbon available to be above or beneath the plane. In conformation C, the carbon atom is pointin beneath the plane of the molecule, and in conformation D the 5-membered ring twists so that the carbon can point above the plane.
| From Construction | From O-a | From O-b | Conformation C | Conformation D |
| 91.519 | 91.471 | 91.514 | 91.477 | 93.943 |
Molecule 6
 |
 |
 |
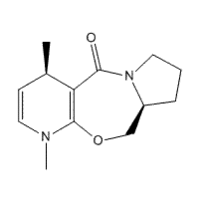
Above, we now have the alkylated product of structure 5. Following the data from before, it is a safe assumption that the carbonyl will always be in its lowest energy when above the plane. Again, there are two possible low-energy conformations that can be adopted by the ring, this time signified by the flipping of the new methyl group from axial to equatorial, but due to being told the methyl group is above the plane, they are actually isomers, with chiral centres. Isomer C has the lowest energy because the methyl group is pointing out of the bend of the molecule, and isomer D has the methyl group pointing into the bend, again resulting in unfavourable steric interactions.
| From Construction | Structural Isomer C | Structural Isomer D |
| -4.720 | -4.306 | -6.553 |
Molecule 7
 |
 |
 |
As with the alkylation of 5 into 6, the alkylation of 7 into 8 is also a stereoselective process. Again, the minimization of the reactant molecule would always result in the carbonyl above the plane of the molecule, although at varying degrees. The most stable angle this time, was close to 23o, causing the nucleophilic attack to occur from beneath the plane. This is due to the steric bulkiness of the nuclephile, that would result in unfavourable interactions if it were to attack from the side with the carbonyl. In 8, the methyl substituent on the 7-membered ring is now in plane with the new nucleophilic substituent, and isopropyl substituent is now facing the opposite direction, as to minimze any destabilizing interactions between the ring substituents. As with the formation of 6, we've two possible isomers of 8 - with the methyl substituent on the 7-membered ring either being above the plane (7-D (endo)) or facing away (7-C (exo)). Isomer D has the higher total energy, because of the unfavourable steric interactions between the methyl group and the 7-membered ring.
| From Construction | Structural Isomer C | Structural Isomer D |
| 158.602 | 156.660 | 165.964 |
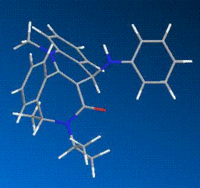
Molecule 8
 |
 |
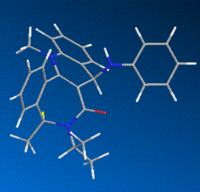 |
The geometry minimization of the product 8 posed a problem for the MMFF94 forcefield initially. The automatic energy minimization by the software produced a structure and energy that looked unfavourable (~90 Eh), and manual rearrangement was required to allow the forcefield to move the conformation out of the high energy minimum. As with the last two molecules, we have two isomers available to us, due to the position of the methyl substituent within the 7-membered ring. Isomer C has the methyl group axial to the ring, and isomer D has the methyl group equatorial to the ring. Due to the steric bulk of the adjacent substituents, isomer C is more stable, as the equatorial (D) isomer has multiple unfavourable interactions.
| From Construction | Structural Isomer C | Structural Isomer D |
| 92.310 | 61.014 | 62.701 |
Synthesis of Taxol
| Parameter | Energy (10-3 Eh) | |||
|---|---|---|---|---|
| Structure | Taxol "9" | Taxol "10" | ||
| Stretch | 4.284 | 2.549 | ||
| Bend | 25.281 | 15.875 | ||
| Stretch-Bend | 0.633 | 0.441 | ||
| Torsion | 29.082 | 30.858 | ||
| Non-1,4 VDW | -1.800 | -2.380 | ||
| 1,4 VDW | 20.205 | 20.100 | ||
| Dipole/Dipole | 0.233 | -0.300 | ||
| Total Energy | 77.916 | 68.663 | ||
 |
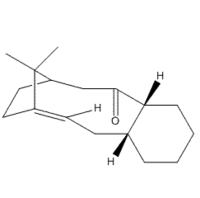 |
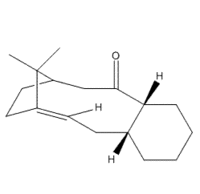
Paclitaxel (TaxolTM) is a common pharmaceutical used in the treatment of various cancer types. It is a natural product derived from the bark of the Pacific Yew, however it destroys the tree in the process. Due to a declining number of sources, it was deemed important to find a viable synthetic route for the production of this drug [1]. The first route deemed practical was propsed by Paquette et al. in 1991 [2] and lists an important intermediate step. We decided to look at this intermediate due to the interesting stereochemistry involved. Our intermediate molecule has an isomer (further called isomer 9 and isomer 10) and the isomers exhibit atropisomerism - the interconversion of the isomers via restricted rotation about a single bond. Isomer 9 contains the carbonyl group pointing up i.e. in the same direction as the bridge, and in the lowest energy conformation the cyclohexane ring is neither chair nor boat - but twist boat/chair. The other isomer has the carbonyl group pointing down, and the lowest energy conformation has the cylcohexane group in the chair conformation.
Initially using the MM2 forcefield, I obtained data for isomer 9, as can be seen in the table. Changing the ring structure from the automatically determined 'twist' to either chair or boat, would cause an increase in total energy, or carbonyl group to change its position. Isomer 10 was more difficult to obtain, as the slightest alteration from a stable configuration would cause the carbonyl to swap direction, and become isomer 9 instead. Through manual alterations, it was possible to find a low-energy conformation of isomer 10, which was made more stable by changing the cyclohexane ring to the chair configuration.
There was a third isomer found, where the carbonyl group was equatorial to the ring, but the energy from this conformation was more than either isomer 9 or 10.
When the MMFF94 forcefield was applied, I started with the conformations that the MM2 forcefield had suggested were of minimum energy. However, without manual alterations to the structure of isomer 10, the MMFF94 calculations showed that isomer 9 was actually of lower energy - opposing conclusions from the MM2 data. After altering the structure around the carbonyl of isomer 10, I managed to decrease the energy in the MMFF94 forcefield to a value beneath that of isomer 9. This is quite simple proof that the forcefields operate differently and take into account different factors when minimizing energy.
The biggest factor which favours isomer 10 is the bending within the molecule. Isomer 9 is bent in two planes, causing it to curve back on itself, increasing the bend energy and also steric hindrance. The next largest component are the 1,4- Van der Waals interactions, which coupled with the high bend energy, indicatess that there are many non-ideal bond angles within these isomers - more so in isomer 9. The reason for the abnormally slow functionalisation of the alkene is that the alkene is bridging and as such is hyperstable i.e. more stable than its respective alkane. This leads to slow reactions at this location and as such unique reaction conditions are required for fast functionalisations.
| Taxol "9" | Taxol "equatorial" | Taxol"10" |
| 77.916 | 128.089 | 68.663 |
Regioselective Addition of Dichlorocarbene
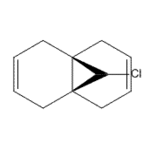 |
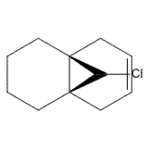 |
We know that reactions are dependent on the respective energies of the reactants, but they can also be dependent on the orbital overlap of the reactants. In order for us to understand certain reactions which we may think occur from an energy-only perspective, but do not occur experimentally, it helps for us to model the orbitals involved. Our methods up until now have involved using the MM2 and MMFF94 forcefields, however these have limitations and are unsuitable for accurately modelling orbitals. Here, we used the MOPAC system with the PM6 method, as this system is much more accurate in calculating electronic systems and bonding within molecules.
In this section, we will look at the molecular orbitals of a diene, and also the predicted vibrations within the molecule and one of it's hydrogenated products.
The MOPAC system is slow at minimizing the energy of a system, and so to speed up the calculations, we initially run the system under the MM2 forcefield, and then run MOPAC-PM6. Regarding reactions, the most important orbitals within a system are most likely the HOMO (Highest Occupied Molecular Orbital), LUMO (Lowest Unoccupied Molecular Orbital), HOMO-1, HOMO-2, LUMO+1 and LUMO+2.
 |
 |
 |
 |
 |
 |
As you can see from the diagrams above, the majority of the electron density is held around the unsaturated carbons, as you'd expect, specifically around the syn-alkene (the alkene bond on the same side of the molecule as the chlorine atom), and in the LUMO states, the density seems to be more localized around the one remaining double bond - the anti-alkene bond (the alkene bond on the opposite side of the molecule as the chlorine atom). Due to this distribution of electronic probability for molecule 12, we'd expect a reaction (i.e. with a dichlorocarbene) to occur at the syn-alkene due to it being highly electron rich, and much more able to donate electron density to the empty orbitals of incoming molecules.
Using the minimized geometries, and the molecules after the MOPAC calculations, I sent my models to the SCAN cluster to calculate the vibrations of the bonds within the two molecules. To simplify the understanding of how the structure of the hydrogenated molecule (molecule 13) is different to the original molecule (molecule 12), we are only going to look at the frequencies of vibration for the C-Cl bonds, and alkene bonds for both molecules.
| Parameter | Energy (10-3 Eh) | |||
|---|---|---|---|---|
| Structure | Molecule 12 | Molecule 13 | ||
| Stretch | 0.820 | 1.424 | ||
| Bend | 7.580 | 7.473 | ||
| Stretch-Bend | 0.062 | 0.022 | ||
| Torsion | 12.186 | 17.130 | ||
| Non-1,4 VDW | -1.713 | -1.692 | ||
| 1,4 VDW | 9.244 | 11.111 | ||
| Dipole/Dipole | 0.178 | 0.113 | ||
| Total Energy | 28.518 | 35.597 | ||
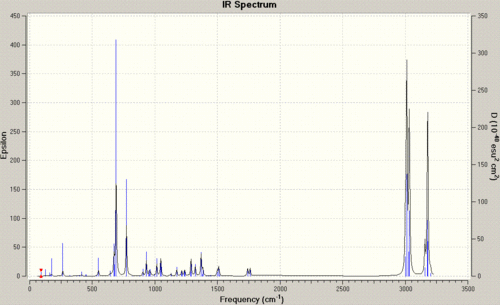
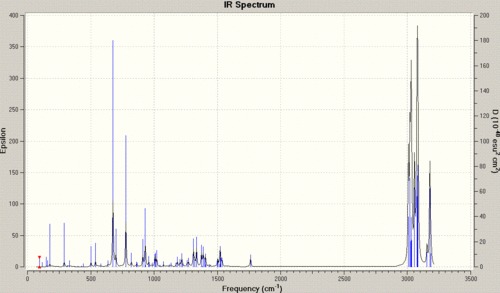
| Stretch | Molecule 12 | Molecule 13 |
| anti C=C | 1740.83Hz | n/a |
| syn C=C | 1760.98Hz | 1761.66Hz |
| C-Cl | 772.59Hz | 776.00Hz |
The data shows in a simple way, how the hydrogenation has altered the vibrations, and as such the bonding, and therefore the electronic distribution within the molecule. Starting with the obvious, we can see that the frequency of vibration for the syn C=C bond in molecule 12 is greater than that for the anti C=C bond. This concurs with the previous assumption of the site of attack, as the weaker bond is the bond with the lower frequency of vibration, and a weaker bond is caused by a lower amount of local electron density, and as such the syn bond is the site of electron donation.
If we now look at the C-Cl bond vibrations, we can initially see that the frequency of the C-Cl vibration for the diene is lower than that of the mono-alkene. This can be explained by looking at the molecular orbitals of the molecules in question. In the diene, we have an anti-alkene bond, which can donate electron density into the anti-bonding orbital of the C-Cl bond. This can in turn weaken the C-Cl bond, lengthening it, and as such reducing the frequency of the vibration. In molecule 13, with no anti-alkene bond ,there is no weakening of the bond and so the frequency of vibration is higher.
 |
 |
Mini-Project
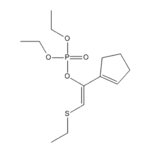 |
 |
As briefly mentioned in the first section of this module, the Diels-Alder reaction is a powerful tool for the formation of cyclic systems, with applications from materials to pharmaceuticals. The main fault of the reaction type is a lack of understanding regarding the stereo- and regiochemistry involved in the reactions. Much time and effort has been spend on finding methods that can force the Diels-Alder to enhance the stereoselectivity of a process. Diels-Alder reactions need not occur with just carbon chains, but also 1,3-dienes with heteroatom substituents will undergo the reaction to form functionalized rings, and are actually known to have enhanced the stereo- and regioselectivity of some Diels-Alder reactions.
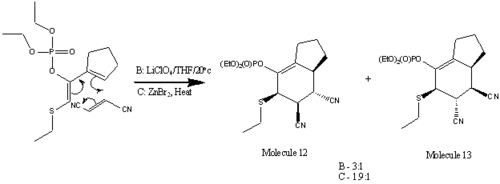
One example of a usable heteroatom substituent is PhS, though such substituents can be unstable in the ideal reaction conditions. Koprowski et al. [3] have highlighted the use of (Z)-1,2-diheterosubstituted-1,3-dienes in Diels-Alder reactions, and such dienes can be unusually stable in highly Lewis acidic conditions. One example is the molecule to the right (known as 1b). Such molecules can be created simply by the reaction between a thiophosphate treated with sodium hydride, and and alkyl halide.
To react with this diene, we need a dienophile which is normally electron withdrawing and will normally have substituents that increase the functionality of the resultant molecule. For this study I will be looking at the reaction between the molecule "1b" and fumaronitrile, in the trans conformation, allowing me to study the likely conformation of the major product.
The strongest orbital interactions in a Diels-Alder reaction are between the HOMO of the diene and the LUMO of the dienophile, and both can be seen below, modelled with MOPAC/PM6. I would have expected to have seen a large amount of electron density on both of the unsaturated carbon-carbon bonds in the diene, but the calculations only show large electron density on the alkene adjacent to the sulphur atom. If you then look at the HOMO-1 for the diene, there is a large amount of electron density on the other alkene bond, leading to a possibility that there are further orbital interactions within the molecule that we cannot account for, or that the dienophile may attack one site, causing a shift in the electron density to the other double bond.
 |
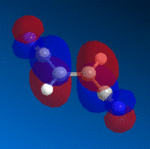 |
Sterics also pose as a large problem in this project, and so I manually rearranged atoms within the system, and set the MM2 forcefield to minimize the energy again. I obtained a new geometry for the diene that now had more correctly aligned bonds, however the new geometry was of a higher energy than the previous structure, and the HOMO still did not show large amounts of electron density on both C=C bonds. From simply looking at the HOMO of the diene, it is impossible to tell which isomer is most likely. The bulky phosphoryloxy group protects one side of the molecule from attack by the fumaronitrile, always leaving one face available, with little hindrance to attack, and as such the next stage is to look at the energy of the two isomeric products.
Using MMFF94 calculations, a suitable low-energy conformation for each isomer has been found. Isomer 12 has a relative energy of -60.841 Eh, whilst isomer 13 has an energy of -71.120 Eh, contradicting the experimental data, which stated that there was an abundance of isomer 12 in the product mixture. This could be due forcefield problems, and not being able to find a suitable low energy conformation, but it is more likely to mean that isomer 13 is the thermodynamic product, and isomer 12 is the kinetic product.
| Carbon Noo | Chemical Shift (ppm) | ||
|---|---|---|---|
| Isomer 12 | Calculated | Experimental | Difference |
| 9 | 133.83 | 134.87 | 1.04 |
| 4 | 130.93 | 129.65 | -1.28 |
| 12 | 115.27 | 117.54 | 2.27 |
| 14 | 114.412 | 116.30 | 1.89 |
| 22 | 62.07 | 64.09 | 2.02 |
| 19 | 61.39 | 64.09 | 2.70 |
| 8 | 50.42 | 43.96 | -6.46 |
| 3 | 46.37 | 43.48 | -2.89 |
| 7 | 39.19 | 37.46 | -1.73 |
| 24 | 34.26 | 31.47 | -2.79 |
| 2 | 33.69 | 30.79 | -2.90 |
| 6 | 32.41 | 28.38 | -4.03 |
| 5 | 28.82 | 26.04 | -2.78 |
| 1 | 25.45 | 22.22 | -3.23 |
| 21 | 17.34 | 15.50 | -1.84 |
| 18 | 16.53 | 15.50 | -1.03 |
| 23 | 13.74 | 14.08 | 0.34 |
| Carbon Noo | Chemical Shift (ppm) | ||
|---|---|---|---|
| Isomer 13 | Calculated | Experimental | Difference |
| 9 | 134.60 | 135.10 | 0.5 |
| 4 | 132.09 | 130.18 | -1.91 |
| 14 | 114.66 | 117.44 | 2.78 |
| 12 | 112.80 | 115.98 | 3.18 |
| 22 | 64.46 | 64.76 | 0.3 |
| 19 | 61.72 | 64.76 | 3.04 |
| 8 | 51.05 | 44.44 | -6.61 |
| 3 | 42.39 | 39.53 | -2.86 |
| 7 | 39.87 | 37.01 | -2.86 |
| 24 | 34.08 | 30.55 | -3.53 |
| 2 | 32.42 | 28.69 | -3.73 |
| 5 | 30.27 | 28.12 | -2.15 |
| 6 | 30.21 | 27.26 | -2.95 |
| 1 | 25.89 | 23.25 | -2.64 |
| 21 | 17.42 | 16.12 | -1.30 |
| 18 | 17.29 | 16.12 | -1.17 |
| 23 | 13.60 | 14.72 | 1.12 |
The two tables here show the 13C NMR data of the two isomers - both experimental and calculated and for accuracy, the difference between the two. The raw data can be found here[4] and here[5], and was gathered using the SCAN cluster, running a DFT with mpw1pw91 subset, and the 6-31g(d,p) basis set. When plainly comparing the experimental data to the calculated shifts, there is a wide range of "difference" values, ranging from ~-6.5 to ~3. However, the majority of points are within 3ppm, and whilst not that accurate, the spectral data still serves its purpose. In both sets of data, there is a point out by circa -6.5ppm, and I believe this to be a forcefield error as opposed to a conformational problem. In both cases, the carbon in question is atom 8 - the carbon adjacent to the sulphur, that is not in the ethyl group. If the problem were due to the conformation, I would have expected much greater deviation from the true data for more points, than just this C-S bond.
When comparing the two sets of spectral data with each other, it is feasible to say that either set could belong to either molecule, and for these isomers, I wouldn't have expected much else. The isomers are only related by simple rotations of simple substituents, and so a big shift would not have been expected. The next set of spectral data supplied in the journal is of 1H NMR, and is not reliable enough to prove one structure from another for this molecule, as there is a wide range of error inherent within calculating and predicting 1H data, unless a lot of processing time is taken, to take into account all of the small details and conformation within the molecule. One option was to run each system through a method which can calculate accurate proton shifts, however this method is pure quantum mechanical, and with each isomer having over 25 atoms, the calculation time would be too great. I expect the reason for the overall bad quality results would be that the molecule was too flexible, and possibly too big. One other anomaly within the spectra is the large number of calculated degenerate carbon atoms for isomer 13, and the total lack of any degeneracy for isomer 12. The experimental data shows that there are two doubly degenerate atom pairs for each isomer, yet the calculations show. I expect that this difference between the experimental and calculated degeneracies is from the conformation of the isomers, but not knowing how the degeneracy is calculated, I cannot make a sure assumption.
 |
 |
 |
However, there still is one tool left to use - and that is the coupling between the hydrogen atoms. The coupling is calculated from bond angles and local substituents, using the Karplus equation, and as such the size of the molecule is no problem. When comparing the two isomers, you would expect that the majority of the couplings are identical, as only a small area of the molecule changes, and this area is the one I decided to look at. On each of the carbons with a cyano substituent, there is also a hydrogen atom, and obviously in a change from axial to equatorial (and vice versa) there will be a large change the coupling between this proton and any protons, 3-bonds away. Using Janocchio, I was able to calculate the 3JHH coupling values between 4 protons - the two protons on the cyano-substituted carbons, and a proton either side of these, resulting in 3 coupling values.
| 3JHH (Hz) | ||
|---|---|---|
| Protons Involved | Isomer 12 (Real) | Isomer 13 (Real) |
| H30/33 | 10.9311 (11.1) | 4.3124 (5.3) |
| H33/34 | 10.9224 (11.3) | 2.3882 (2.9) |
| H34/35 | 3.6978 (4.0) | 0.8618 (1.2) |
 |
It is clear to see that the coupling constants for isomer 12 are much greater than those for isomer 13 in this region. What is interesting to see is that there is little difference between the H30/33 coupling and the H33/34 coupling for isomer 12, but it makes sense, when thought through. The reason why both values are high and similar, is that both couplings are occurring over a ~180o angle, as the protons are in axial positions. We don't see this in isomer 13 as the hydrogen atoms are equatorial, and the bond angles are then between 40o to 60o, and the reason for the low H34/35 coupling in isomer 12 is that the bond angle is reaching 90o, causing the cosine parts of the Karplus equation to reach 0.
When comparing the calculated constants to those found from the experimental data, you can see that this process is more accurate than using either the 13C or 1H NMR, and can be easily used to discriminate between the products, as the couplings are unique and very far apart. Therefore, from an experimental point of view, the easiest way to work out which product you have is to take a proton NMR, to ignore the peak locations, and just look at the coupling.
Conclusion
I think that this small project itself has been a success, even though the results are not accurate enough for more detailed studies. I aimed to deduce the most stable isomer by looking at the available HOMO and LUMO for this reaction. Although I found that it was impossible to tell from looking, which way the fumaronitrile was most likely to attack, it helped my understanding of the reaction, and with more time, I expect I would be able to find the most likely product, by modelling the possible transition states. The most stable intermediate molecule is going to be the one for isomer 12, as the forcefield data shows that the most stable product is actually isomer 13 and because more of isomer 12 is produced, the reaction here is kinetic, and dependent on the intermediate.
The carbon NMR was disappointing with regards to its accuracy, but it also helped outline the limitations and problems with the methods used, especially if the data was gathered for a molecule that had no experimental data yet. For example, the software calculated no degeneracy within either molecule, though the experimental data confirms that there are degenerate carbons. Again, with more time, I expect that I would've been able to produce much more accurate results with regards to the 13C spectra, by altering the isomers to more stable forms, reducing their flexibility.
Without accurate spectral data to differentiate between the two molecules, it was of a great help to find the 3JHH values to be so unique to each molecule. Computational techniques are reliable enough now to be used in conjunction with experimental data, even if just to check the spectra. Even with data such as mine, if there was a large erroneous result, it would be obvious, and the reaction can be restarted under different conditions, for example.
Key Literature and Data
- ↑ Goodman, Jordan; Walsh, Vivien (2001). The Story of Taxol: Nature and Politics in the Pursuit of an Anti-Cancer Drug. Cambridge University Press. ISBN 052156123X.
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
- ↑ M. Koprowski, A. Skowrońska, M. L. Główka and A. Fruziński, Fully regio- and endo-stereoselective synthesis of new polycyclic allylic sulfides via a Diels-Alder reaction. Synthetically useful transformations of these sulfides: DOI:10.1016/j.tet.2006.11.049
- ↑ NMR data for molecule 12 DOI:10042/to-3721
- ↑ NMR data for molecule 13 DOI:10042/to-3704
- Another well known example is within Vancomycin: J. Am. Chem. Soc., 1999, 121, 3226. DOI: [http://dx.doi.org/10.1021/ja990189i 10.1021/ja990189i
Molecule P13
http://hdl.handle.net/10042/to-3704
