Rep:Mod:Al7215 Yr2MO
BH3 Molecule
Method: B3LYP/6-31G(d,p)
Item Table
Item Value Threshold Converged? Maximum Force 0.000189 0.000450 YES RMS Force 0.000095 0.000300 YES Maximum Displacement 0.000746 0.001800 YES RMS Displacement 0.000373 0.001200 YES
IR Frequencies
Low frequencies --- -0.2263 -0.1037 -0.0054 47.9770 49.0378 49.0383 Low frequencies --- 1163.7209 1213.6704 1213.6731
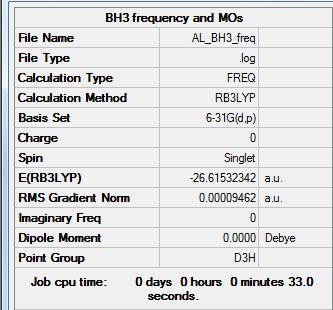
Frequency analysis log file:BH3_frequency.log
Optimised Borane Molecule |
IR Spectrum
| Wavenumber (cm-1) | Intensity (arbitrary units) | Symmetry | IR Active | Type of Vibration |
| 1164 | 92 | A2" | Yes | Out-of-plane bend |
| 1214 | 14 | E' | Very slight | In-plane bend |
| 1214 | 14 | E' | Very slight | In-plane bend |
| 2580 | 0 | A1' | No | Symmetric stretch |
| 2713 | 126 | E' | Yes | Asymmetric stretch |
| 2713 | 126 | E' | Yes | Asymmetric stretch |
There are less than 6 peaks as two of the asymmetric stretches at 1214 cm-1 and 2713 cm-1 have twofold degeneracy while the symmetric stretch at 2580 cm-1 is IR inactive and does not register a peak.
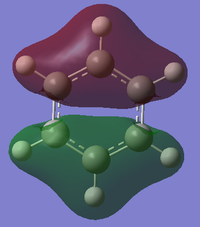
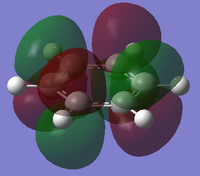
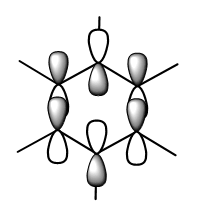
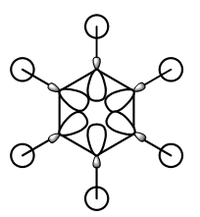
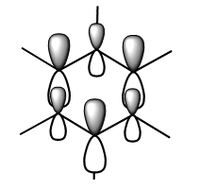
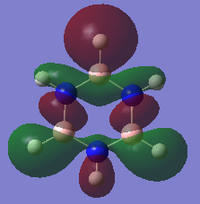
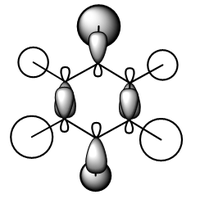
MO diagram for BH3
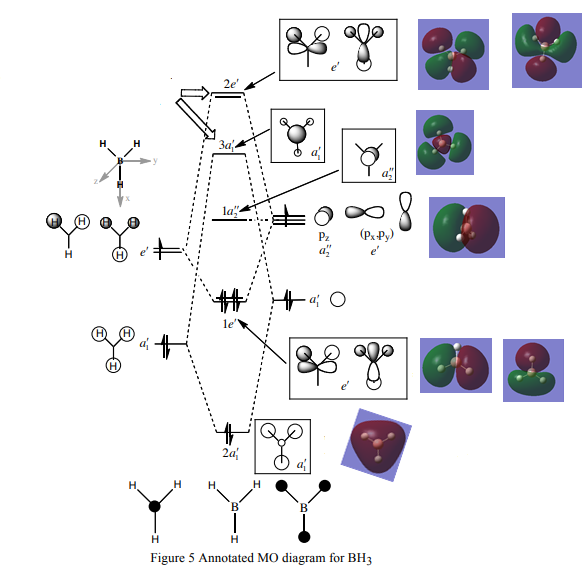
There is a slight difference in the LCAO and real MOs with A1' symmetry as the central lobe is much smaller and the adjacent green lobes are much larger for the real MO than the LCAO MO. Other than that, there are no significant differences between the real and LCAO MOs. This shows that the LCAO theory is a fairly good method to predict molecular orbitals for an unknown simple molecule without having to do complicated calculations.
Smf115 (talk) 23:59, 16 May 2018 (BST)Clearly presented MOs and good discussion of both the similarities and differences of the LCAOs and the MOs.
NH3 and NH3BH3 (Key Data)
NH3 Molecule
Method: B3LYP/6-31G(d,p)
Item Table
Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000014 0.001800 YES RMS Displacement 0.000009 0.001200 YES
IR Frequencies
Low frequencies --- -11.6527 -11.6490 -0.0045 0.0333 0.1312 25.5724 Low frequencies --- 1089.6616 1694.1736 1694.1736
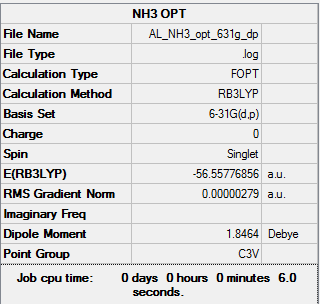
Frequency analysis log file: NH3_frequency.log
NH3BH3 Molecule
Method: B3LYP/6-31G(d,p)
Item Table
Item Value Threshold Converged? Maximum Force 0.000125 0.000450 YES RMS Force 0.000059 0.000300 YES Maximum Displacement 0.000614 0.001800 YES RMS Displacement 0.000313 0.001200 YES
IR Frequencies
Low frequencies --- -10.8522 0.0004 0.0009 0.0013 19.1618 42.3732 Low frequencies --- 266.1846 632.1840 638.2497
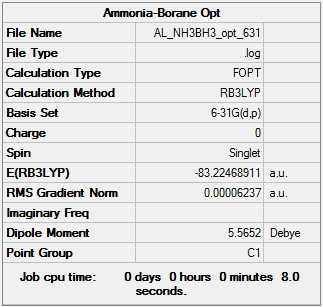
Frequency analysis log file: NH3BH3_frequency.log
Reaction Energies of Ammonia-Borane
Reaction: NH3 + BH3 -> NH3BH3
E(NH3) = -56.55776856 a.u. = -56.55778 a.u. (5 d.p.)
E(BH3)= -26.61532342 a.u. = -26.61532 a.u. (5 d.p.)
E(NH3BH3)= -83.22468911 a.u. = -83.22469 a.u. (5 d.p.)
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]= -0.05160 a.u. = -135 kJ/mol
The association energy of Ammonia-Borane is about -135 kJ/mol while its dissociation energy is 135 kJ/mol. Hence, B-N dative bond is weak as its dissociation energy is lower than that of a C-C bond, which is about 350 kJ/mol.
Smf115 (talk) 23:58, 16 May 2018 (BST)Good calculation but references required when quoting bond dissociation energies.
BBr3 Molecule
Method: B3LYP/6-31G(d,p) [Boron] & LanL2DZ [Bromine]
Item Table
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000018 0.001200 YES
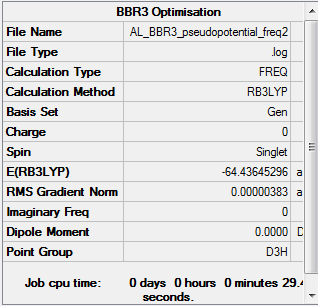
Frequency analysis log file:BBr3_frequency.log
DSpace link: DOI:10042/202305
IR Frequencies
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
Investigating Aromaticity (Mini-project)
Optimisation and Frequency Analysis of Benzene and Borazine
Benzene molecule
Method: B3LYP/6-31G(d,p)
Item Table
Item Value Threshold Converged? Maximum Force 0.000194 0.000450 YES RMS Force 0.000077 0.000300 YES Maximum Displacement 0.000824 0.001800 YES RMS Displacement 0.000289 0.001200 YES
IR Frequencies
Low frequencies --- -2.1456 -2.1456 -0.0088 -0.0040 -0.0040 10.4835 Low frequencies --- 413.9768 413.9768 621.1390
Frequency analysis log file:Benzene_frequency.log
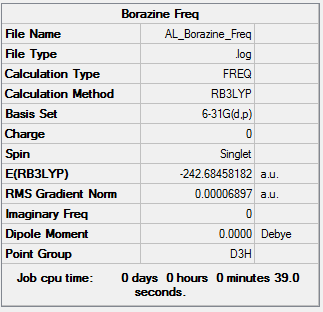
Borazine molecule
Method: B3LYP/6-31G(d,p)
Item Table
Item Value Threshold Converged? Maximum Force 0.000217 0.000450 YES RMS Force 0.000069 0.000300 YES Maximum Displacement 0.000333 0.001800 YES RMS Displacement 0.000106 0.001200 YES
IR Frequencies
Low frequencies --- -12.5651 -12.3512 -8.8739 -0.0100 0.0382 0.0785 Low frequencies --- 289.1192 289.1283 403.9050
Frequency analysis log file:Borazine_frequency.log
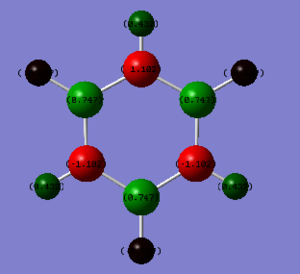
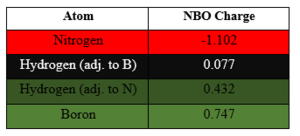
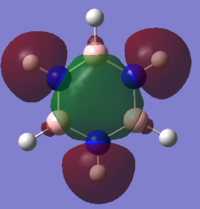
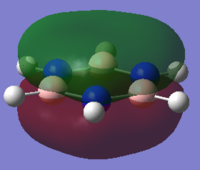
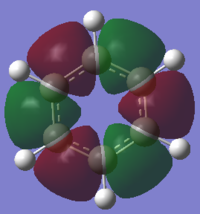
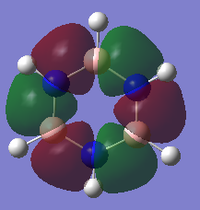
Charge Analysis of Benzene and Borazine
| Colour Range |
|---|
|
| Charge distribution | ||
|---|---|---|
|
|
The specific Natural Bond Orbital (NBO) charges were analysed for the optimised benzene molecule. Hydrogen has a positive charge of 0.239 while carbon has a negative charge of -0.239. This charge distribution is expected as carbon is more electronegative than hydrogen, thus leading to the withdrawal of electron density from hydrogen to carbon. Additionally, all 6 hydrogen and carbon atoms have the same charge magnitude as benzene is highly symmetrical, with equal C-H bond lengths. |
|
|
The specific NBO charges were also analysed for the optimised borazine molecule. Unlike benzene, all the ring atoms do not have the same charge as the ring is composed of two different atoms, nitrogen and boron. Overall in the whole molecule, nitrogen is the most electronegative atom with a charge of -1.102, while boron is the most electropositive atom, with a charge of 0.747. The charge on the hydrogen atom also varies depending on the adjacent ring atom. The hydrogen adjacent to nitrogen is more positively charged compared to the hydrogen adjacent to boron. This is as nitrogen is more electronegative than boron and pulls electron density away from the hydrogen atom to a greater extent, making it more positive. |
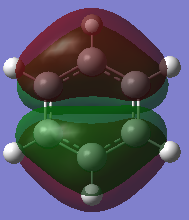
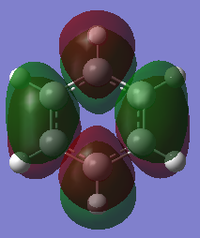
MO Analysis of Benzene
| No. | Molecular Orbital | LCAO Analogue | Energy (a.u.) | Description |
|---|---|---|---|---|
| 9 | 
|
|
-0.74005 | Molecular orbital (MO) 9 is a low energy, occupied MO of Benzene. This MO has in-phase bonding interactions between all connected carbon 2s and hydrogen 1s AOs, but anti-bonding interactions between one half of the molecule and the other half. Overall, the interaction is bonding, with a planar node runnning through the center of the molecule. |
| 22 | 
|
|
0.00267 | Molecular orbital (MO) 22 is a Lowest Unoccupied Molecular Orbital (LUMO) of Benzene. This MO has in-phase bonding interactions between the pAOs at C2 and C3, as well as at C5 and C6. However, these two pairs have antibonding interactions with pAOs at C1 and C4. The overall interaction is antibonding, with 3 nodes present. |
| 24 | 
|
|
0.09117 | Molecular orbital (MO) 24 is an even higher energy, unoccupied MO of Benzene. This MO has anti-bonding interactions between all carbon sigma 2p AOs and hydrogen 1s AOs. The overall interaction is anti-bonding, with two circular nodal regions. Due to its large size and presence of nodal regions, it is high in energy. |
Smf115 (talk) 23:57, 16 May 2018 (BST)Great extra analysis of some of the MOs of both of the molecules and the corresponding LCAOs.
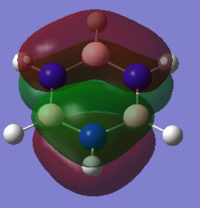
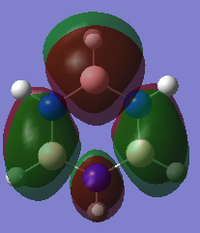
MO Analysis of Borazine
| No. | Molecular Orbital | LCAO Analogue | Energy (a.u.) | Description |
|---|---|---|---|---|
| 10 | 
|
|
-0.55131 | Molecular orbital (MO) 10 is a low energy, occupied MO of Borazine. This MO has bonding interactions between 2pz AOs of nitrogen and 2s AOs of hydrogen. Also, all nitrogen and boron 2p AOs are pointing radically inwards, with nitrogen 2p AOs being bigger than that of boron as it is more electronegative. The overall interaction is bonding. |
| 17 | 
|
|
-0.36129 | Molecular orbital (MO) 17 is also a low energy, occupied MO of Borazine. This MO has in-phase bonding interactions between all 2p AOs of nitrogen and boron, which are placed at alternating positions around the ring. The overall interaction is bonding, with a planar node at the inter-nuclear region. |
| 18 | 
|
|
-0.31995 | Molecular orbital (MO) 18 is a slightly higher energy, occupied MO of Borazine. This MO has the following bonding interactions: 1. Between sigma pAOs of nitrogen and boron at C2 and C3, as well as C5 and C6 respectively; 2. Side-on overlap of 2p and 1s AOs at C2, C3, C5 and C6; 3. Between nitrogen's 2p orbital at C4 and hydrogen's 1s orbital; 4. Between Boron's 2p orbital at C1 and a slightly more diffused hydrogen 1s orbital. The overall interaction is bonding, with several nodes present at the B and N atoms. |
Comparing MOs of Benzene and Borazine
| Benzene | Borazine | Discussion |
|---|---|---|
 MO 21
|
 MO 21
|
MO 21 is the Highest Occupied Molecular Orbital (HOMO) for both complexes. It is doubly degenerate with MO 20, with energy of -0.24691 a.u. for benzene and -0.27590 a.u. for borazine. Both MOs have in-phase bonding interactions among 3 connected 2pz AOs on either sides of the molecule, with anti-bonding interactions between the two halves. Both MOs also have an overall bonding interaction, with two nodes present. The difference lies in borazine MO being less symmetric than benzene MO due to varying number of nitrogen and boron atoms on either side of the molecule. |
 MO 22
|
 MO 22
|
MO 22 is the LUMO for both complexes. It is doubly degenerate with MO 23, with energy of 0.00267 a.u. for benzene and 0.02422 a.u. for borazine. This MO has in-phase bonding interactions between the pz AOs at ring atoms at positions 2 and 3, as well as at positions 5 and 6. However, these two pairs have antibonding interactions with pz AOs at positions 1 and 4. Both MOs have an overall antibonding interaction, with 3 nodes present. For a bonding MO, the electron cloud should be polarised towards nitrogen because it is more electronegative than boron. However, the reverse is seen for this borazine MO as it is antibonding. This is absent in benzene due to no electronegativity difference between the carbon ring atoms. |
 MO 14
|
 MO 15
|
MO 14 and 15 are low energies, occupied MOs of benzene and borazine respectively. Both MOs have a mix of bonding and antibonding interactions due to sigma pAOs of the ring atoms. Like benzene, the MO of borazine is highly symmetric despite the electronegativity difference of nitrogen and boron. Moreover, there is slightly less overlap in borazine due to orbital mismatch. Both MOs have an overall bonding interaction. |
Concept of Aromaticity
The concept of aromaticity began with the isolation of benzene by Michael Faraday in 1825. Since then, many criteria or definitions for characterising aromaticity have been considered. The following lists a few of these criteria:[2]
1. Chemical behaviour: Electrophilic aromatic substitution- Such reactions is generally as it conserves the pi-electron structure of aromatic compounds;
2. Energetic: Large resonance energy- Aromatic compounds have enhanced stability compared to their olefinic analogues;
3. Structural properties: Bond length equalisation due to cyclic delocalisation;
4. Magnetic: “ring current” effects which include: analogous chemical shifts, large magnetic anisotropies and diamagnetic susceptibility exaltation
Overlapping pz AOs requires the planarity of a molecule. This, compared to those ascribed above, is not a good descriptor of aromaticity as lots of aromatic compounds are non-planar. A few good examples include: para- and meta- cyclophanes, pyrenophanes, or per-substituted derivatives of polyacenes.[3]
While aromaticity is not a property that is directly observable and lacks a well-founded physical basis, the computation of real MOs can help with the basic quantification and qualitative understanding of this fundamental chemical concept. For instance, real MOs can help to ascertain the high symmetry of aromatic compounds. This is certainly helpful as most archetypal aromatic compounds are highly symmetrical and possess degenerate HOMOs that are fully occupied, resulting in a closed-shell structure or have the same spin half-filled electronic structure.[4] (As seen earlier, benzene and borazine have HOMOs that are doubly degenerate)
Electron delocalisation is also an important aromatic descriptor that can be aided by localising real MOs and finding regions in which electron pairs are located. To date, the NBO analysis, used for calculation of charge distribution in benzene and borazine, is one of the most viable methods for localising bonds and lone pairs.[5]
Smf115 (talk) 23:56, 16 May 2018 (BST)Great discussion covering a range of points and with own literature referenced.
Smf115 (talk) 00:00, 17 May 2018 (BST)Overall a thorough report with a very good project section.
- ↑ Patricia A.Hunt, Problem Class 1 Answers, p.3
- ↑ Pure & Appl. Chem., Vol. 68, No. 2, pp. 209-218, 1996
- ↑ M. Palusiak, TM. Krygowski, Chemistry., 2007, 13, 7996-8006.
- ↑ F. Feixas, M. Eduard, P. Jordi, S. Miquel, Chem. Soc. Rev., 2015, 44, 6434
- ↑ F. Feixas, M. Eduard, P. Jordi, S. Miquel, Chem. Soc. Rev., 2015, 44, 6434