Rep:Mod:Aguire
Introduction to Molecular Modelling 2 (Laurin Rupp CID:01357674)
Throughout this page, the numerical and graphical results obtained via gaussview will be displayed and explained. The focus of this page was on the molecules NH3, N2, H2, and PH5.
NH3
First of all some basic question about the molecule were answered:
- What is the molecule? NH3
- What is the calculation method? RB3LYP
- What is the basis set? 6-31G(d.p)
- What is the final energy E(RB3LYP) in atomic units (au)? -56.55776873
- What is the RMS gradient? 0.00000485
- What is the point group of your molecule? C3V
It was also discovered that the N-H bond length was equal to 1.01798 Å, and that the H-N-H bond angle was equal to 105.741°, which was as expected since in a tetrahedral molecule bond angles should be 120 degrees, but due to the lone pair of electrons that are closer to the central nitrogen atom and repel the other bonds strongly, the H-N-H bond angles decrease.
It was also checked weather the molecule had really been optimised:
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986279D-10
Optimization completed.
-- Stationary point found.
From this it can be deduced that since all the forces are positive and converge, a minimum energy and hence an optimised molecule has been found. The full NH3 optimised *.log file can be found here
test molecule |
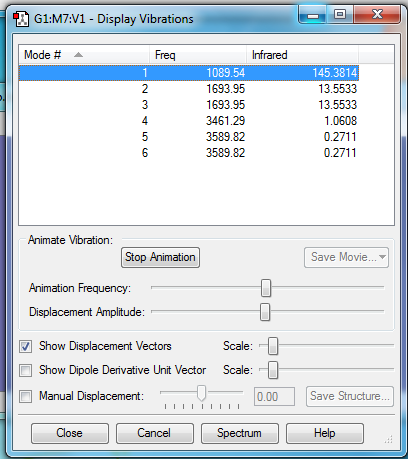
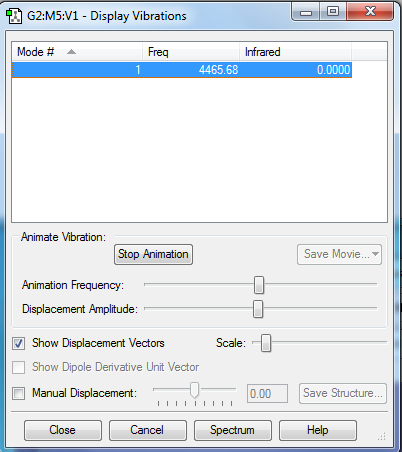
A vibrational analysis of the molecule was also carried out:
- How many modes do you expect from the 3N-6 rule? 6
- Which modes are degenerate (ie have the same energy)? Mode 2 and 3 have the same energy, and mode 5 and 6 also have the same energy. So overall there are only 4 distinct modes.
- Which modes are "bending" vibrations and which are "bond stretch" vibrations? Bending vibrations are lower frequency, hence we can assume that modes 1-3 correspond to bending vibrations, and frequencies 4-6 correspond to stretching vibrations.
- Which mode is highly symmetric? Mode 1 is a highly symmetric bending vibration, and mode 4 is a highly symmetric stretching vibration.
- One mode is known as the "umbrella" mode, which one is this? The first mode
- How many bands would you expect to see in an experimental spectrum of gaseous ammonia? 4, since that is the number of distinct vibrational frequencies.
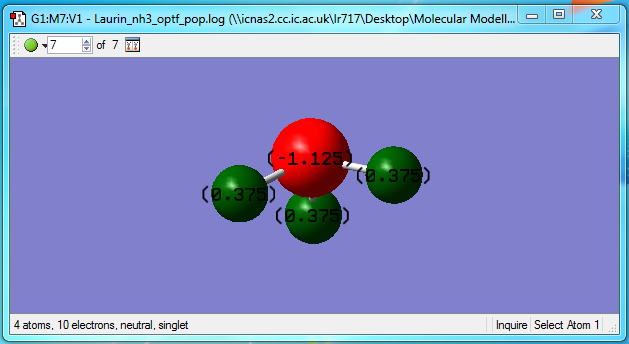
From this diagram we can see that the charge on the Nitrogen atom in our optimized molecule is -1.125, because it is more electronegative than the hydrogens, who each have a charge of +0.375
N2
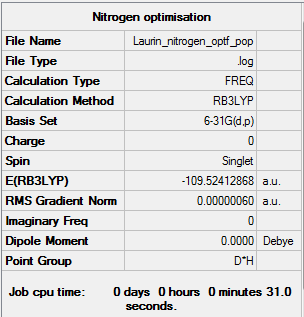
From the summary of the calculations its can be seen that the N2 is much higher in energy due to the triple bond. The bond length of the optimized molecule was found to be 1.10550 Å, and obviously since it is a diatomic molecule, no bond angle can be determined.
As for NH3, the same checks and types of analysis were performed:
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.383779D-13
Optimization completed.
-- Stationary point found.
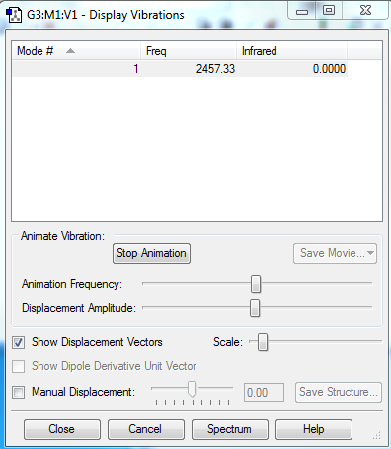
Since N2 is a homogeneous diatomic molecule, only one kind of vibrational frequency is observed:
My N2 optimised *.log file can be found here
test molecule |
H2
The hydrogen molecule is much lower in energy, and has a bond length of 0.74279 Å
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.167770D-13
Optimization completed.
-- Stationary point found.
My H2 optimised *.log file can be found here
test molecule |
Reaction Energy
N2 + 3H2 → 2NH3
- E(NH3)= -56.55776873 Au
- 2*E(NH3)= -113.11553764 Au
- E(N2)= -109.52412868 Au
- E(H2)= -1.17853936 Au
- 3*E(H2)= -3.53561808 Au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579088 Au = -146.47895544 kj/mol
NH3 is more stable because it is lower in energy than it's two components, hence the negative ΔH of the reaction, indicating that it is exothermic.
Project Molecule: PH5
For the last part of this project the analysis of PH5 was attempted.
Item Value Threshold Converged?
Maximum Force 0.000009 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000009 0.001200 YES
Predicted change in Energy=-6.688004D-10
Optimization completed.
-- Stationary point found.
In this case there were two different bond lengths: the 3 equatorial hydrogen atoms each had a bond length of 1.43316 Å, whereas the two axial hydrogens had a slightly longer bond length of 1.48687 Å.
As expected the bond angles were 90° between axial and equatorial hydrogens, and 120° in-between equatorial hydrogens.
My PH5 optimised *.log file can be found here
test molecule |
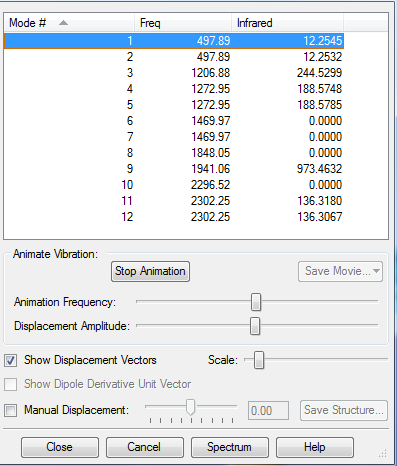
- How many modes do you expect from the 3N-6 rule? 12
- Which modes are degenerate (ie have the same energy)? Mode 1 and 2, 4 and 5, 6 and 7, and 11 and 12 are degenerate. Hence there are only 8 distinct vibrational frequencies.
- Which modes are "bending" vibrations and which are "bond stretch" vibrations? Bending vibrations are lower frequency, hence we can assume that modes 1-7 correspond to bending vibrations, and frequencies 8-12 correspond to stretching vibrations, which was confirmed by looking at the vector animation.
- Which modes are highly symmetric? Mode 8 and 10 are highly symmetric stretching vibrations.
- How many bands would you expect to see in an experimental spectrum of gaseous ammonia? 8 (since that is the number of distinct vibrational frequencies).
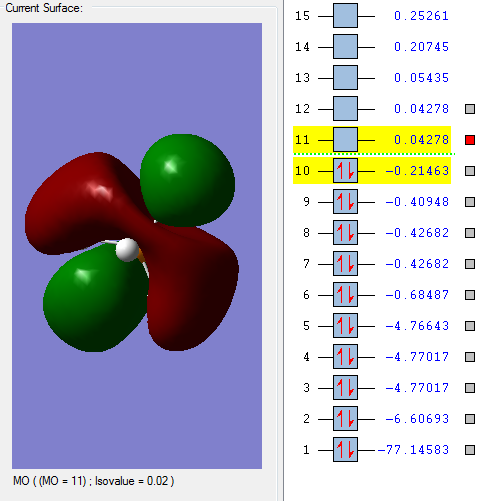
In this diagram the 3 hydrogens at 120° from each other are highlighted in blue because they were completely black and invisible in the original charge distribution diagram. The Phosphorus atoms is more electropositive than the hydrogen atoms and hence pushes the electron density away from itself and toward the hydrogens.
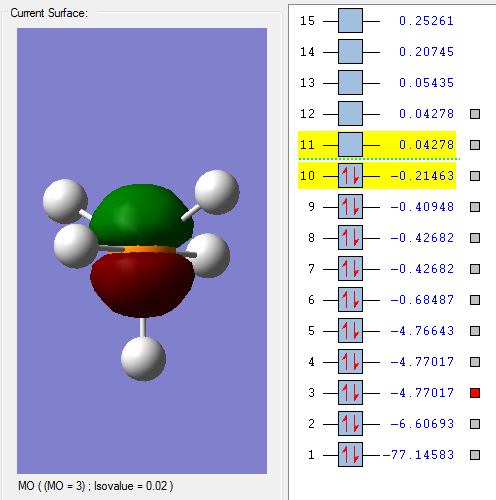
This molecular orbital is mostly made up of the 2px atomic orbital of the Phosphorous, and is not really interacting with the 1s from the hydrogens because the energy difference is too great (the 2px orbital is too deep in energy). Looking at the optimized *log file, we can see that this is indeed the case as the molecular orbital is over 99% mad up of the 2px atomic orbital.
This molecular orbital is mixture of different s orbitals. It is mainly made up of the Phosphorus 3s orbital (around 60%), and also 4s orbitals, which interact with the hydrogen 1s orbitals. This is a bonding orbital, but still quite deep in energy so that orbital overlap is still not very good.
This is a bonding orbital with much better overlap than the previous ones, as it is close to the HOMO. It is mainly made up of 3pz atomic orbital from the Phosphorous (around 50% contribution), and als slightly influenced by the 2pz and 4 pz. These atomic orbitals overlap with each other and the axial hydrogen 1s and 2s orbitals. It is interesting because the 2s hydrogen orbital has a similar contribution to the overall molecular orbital as the 1s hydrogen orbital.
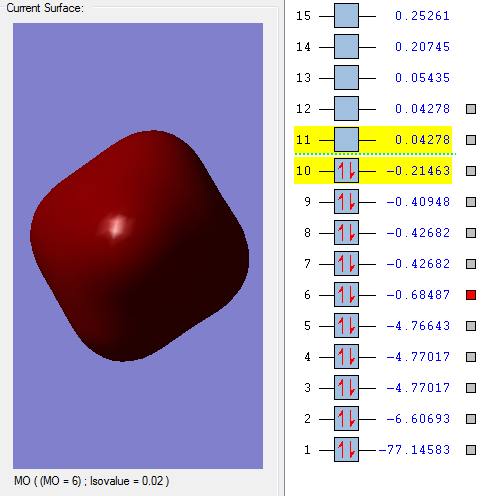
This is the HOMO bonding orbital, and is very interesting because it seems to be mainly an overlap between the 5dz² phosphorus orbital, which should be unoccupied according to the aufbau principle, and the hydrogen 1s and 2s orbitals. This might be because it is extremely spatially favorable, as the trigonal bipyramidal structure mirrors the dz² shape. The best overlap seems to be between the axial 2s orbitals and the 5dz² orbital,which is stronger that the equatorial hydrogen overlap (due to the shape of the dz² orbital).
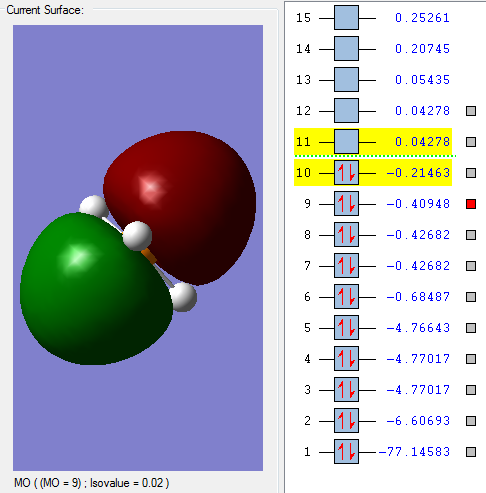
This is the LUMO antibonding orbital. It is mainly made up of a 4px orbital from the phosphorus (as well as the 1px and 2px, which overlaps with a 2s orbital from the axial hydrogens. The equatorial hydrogens do not really contribute to this antibonding orbital. There also seems to be a bit of 5dxy contribution from the phosphorus and 2px from the axial hydrogens (if only very slightly).