Rep:Mod:Ab mod3
The Cope Rearrangement
Sigmatropic rearrangements are a pericyclic reaction in which a σ-bonds is changed to another through an intramolecular process. An example of a sigmatropic reaction is the [3,3]-Cope rearrangement.
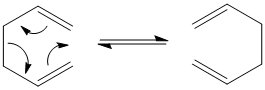
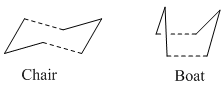
1,5-hexadiene can undergo a Cope rearrangement via a "chair" or "boat" transition structure. The "boat" transition structure is meant to be higher in energy than the "chair" structure. This will be analyzed using GuassView below. The reasons for why the "boat" structure is higher in energy may be due to the fact that the atoms are too close together and therefore have steric repulsion.
Optimisating reactants and products
Initially the reactants and products were made drawn and optimised in GuassView and these calculations can be compared to the experimental values. A molecule of 1,5-hexadiene can be in either the 'anti' or 'gauche' conformation depending on the arrangement of the middle four carbons (C2-C3-C4-C5). All conformers were optimised using Hartree-Fock, 3-21G method.
Antiperiplanar
A molecule of 1,5-hexadiene was drawn out in GuassView with an 'anti' linkage across the central four carbons. The optimised molecule was then compared to the molecules in the index to deduce which conformer had been produced.
Item Value Threshold Converged? Maximum Force 0.000031 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000570 0.001800 YES RMS Displacement 0.000166 0.001200 YES Predicted change in Energy=-1.183326D-08 Optimization completed. -- Stationary point found.
Symmetry
Point group= C2h
Gauche
Item Value Threshold Converged?
Maximum Force 0.000019 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000672 0.001800 YES RMS Displacement 0.000162 0.001200 YES Predicted change in Energy=-2.586982D-08 Optimization completed. -- Stationary point found.
Symmetry
Point group= C2
Alternative gauche conformer
The dihedral angle can be altered to give a different gauche conformer with C2 symmetry:
Ci Anti2
Item Value Threshold Converged? Maximum Force 0.000047 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.000599 0.001800 YES RMS Displacement 0.000257 0.001200 YES Predicted change in Energy=-2.590044D-08 Optimization completed. -- Stationary point found.
B3YLP/6-31G*
The optimised Ci structure was reoptimised using B3LYP/6-31G* method and compared to the HF/3-21G optimised structure. The B3LYP/6-31G* method is a much more accurate way of determining the structure because it is able to involve a higher level of calculations and thus gives a better representation.
| ' | Ci (HF/3-21G) | Ci (B3LYP/6-31G) |
| Total energy (Hartrees) | -231.69254 | -234.62319422 |
| C=C bond length (Å) | 1.316 | 1.337 |
| C-C bond length (Å) | 1.509 | 1.505 |
Summary of conformers
From the table below it can been seen that the computed methods and the apendix values were in good agreement. The table also shows that the anti2 configuaration is the lowest in energy, this is due to the fact that the gauche conformers involve steric clash between the larger end groups which is not present in the anti conformer.
Vibrational analysis
Additional frequency calculations need to be carried out in order to be able to compare the energies with experimental quantities. The optimised B2LYP/6-31G* structure was used to run the frequency calculations. The thermochemistry results from the output file can be seen below:
Sum of electronic and zero-point Energies (E=Eelec+ ZPE)= -234.481064 Sum of electronic and thermal Energies (E= E+ Evib+ Erot+ Etrans)= -234.473713 Sum of electronic and thermal Enthalpies (H= E+ RT)= -234.472768 Sum of electronic and thermal Free Energies (G= H- TS)= -234.512636
Optimising the "Chair" and "Boat" Transition Structures
The transition structures for the 'chair' and 'boat' conformations are both drawn by using two C3H5 allyl fragments and optimised using three different methods, all of which will be explored in turn below.
Chair Transition Structure
A guess structure was drawn in GuassView and used as the starting point for the calculations. The distance between the two allyl fragments was set to roughly 2.2Å. Transition state calculations involve finding the negative direction of the curvature and can be worked out most accurately using force constants, however this will not work if the guess structure is significantly different to the transition structure. In this situation, it is better to use the freeze coordination method which allows the rest of the molecule to relax first and then finds the transition state.
The Guess structure was optimised to a Transition State (Berny) using Hartree Fock and 3-21G basis set.DOI:10042/to-12412

One imaginary frequency of -817.96cm-1 with an intensity of 5.87. As seen from the above animation, this imaginary frequency directly relates to the cope rearrangement with the formation of one σ bond whilst simultaneously breaking the other σ bond.
Freeze Coordinate method
The transition strusture can also be optimised using the freeze coordinate method. The guess structure was opened in a new file on GuassView, the bond between the new bond forming carbons were frozen at 2.2Å and then optimised using HF/3-21G. This step allows the rest of the atoms to relax whilst freezing the terminal carbons are frozen in their place.
The fchk output file of this is then optimised further by changing the frozen bonds into derivates, therefore allowing them to move so they can form the optimum transition structure. This transition structure was compared to the one worked out using the force constants method, a summary of which can be seen below:
| ' | Force constant method | Freeze coord. Method |
| Energy (Hartrees) | -231.61932 | -231.61932 |
| Gradient (Hartrees) | 0.00001022 | 0.0000549 |
| Terminal bond distance | 2.02029 | 2.0199 |
| Structure | Jmol | Jmol |
From the table above, it can be deduced that the energies are very similar, however there is a difference in the terminal C-C length. The force constant method produces a larger difference between these carbons, however has a lower gradient therefore a more accurate representation of the transition structure. However the force constant method can not always be used for larger molecules.
Boat Transition Structure
The boat transition structure is optimised using the QST2 method. The involves specifying the reactants and products by numbering them specifically and then the program with find a structure between the two. The original Ci reactant molecule was used to create the reactant and product. Opt+Freq calculations were then carried out on this molecule using the TS(QST2) option. The result of this calculation shows the molecule below which is obviously incorrect.
This is because the program does not consider the ability to rotate around the central C-C bond. Therefore, if we go back and change the dihedral angle for C2-C3-C4-C5 to 0° and then change the angles between C2-C3-C4 and C3-C4-C5 angles to 100° for both the reactant and products and re-run the TS(QST2) calculation the Transition state should be found. DOI:10042/to-12419
IRC
The Intrinsic Reaction Coordinate method is a method which allows you to follow the potential energy surface for the minimum energy path from the transition structure to the local minimum.
Chair
The optimised chair transition structure was opened in GuassView. As the reaction is symmetrical, only the forward direction is calculated. The number of points on the IRC curve was increased to 50 and the IRC calculations were run. The resulting output file was opened and the structure was compared to that of the gauche2 conformer.

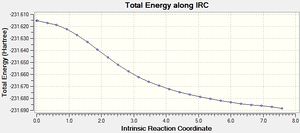

From the graphs above it can be seen that the progression of the points along the IRC leads to a structure with low energy and a gradient close to zero. This relates to the local minimum and is reached by taking steps in the direction with the steepest gradient. Initially the energy drops rapidly until small changes to the structure result in slightly lower energies. The summary of the lowest energy structure can be seen below.
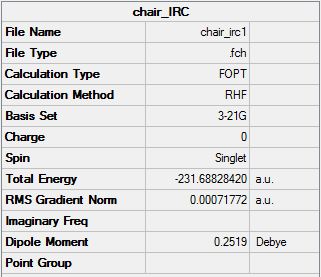
IRC opt
The final structure from the IRC above may not be the one with the minimum geometry therefore this molecule can then be optimised further using the three different methods explored below.
(i) The last point of the IRC is minimised
The last point of the IRC was taken and optimised using Hartree-Fock method with 3-21G basis set. The resulting molecule had C2 symmetry, therefore it can be related to the gauche2 structure in the reactants and products table above. The energy of this minimum is -231.69167 Hartrees, this value directly links to the appendix value (-231.69167) therefore it can be assumed that the minimum reached is of the gauche2 conformation.
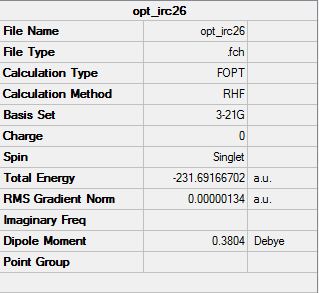
A disadvantage of this method is that one can not be sure if the correct minimum has been reached. This is due to the fact that this calculation will take you to the closest minimum which may not always be the lowest minimum.
(ii) Increasing the number of points on the IRC
The second method of optimising involved increasing the number of points on the IRC curve. This can be done in an effort to increase the number of points thus allowing a minimum to be reached. However only 26 points were found on the output file and the same geometry of the molecule was given. The energy for this molecule can be compared to the energy of the IRC carried out initially and both give the same total energy of -231.68828 Hartrees.

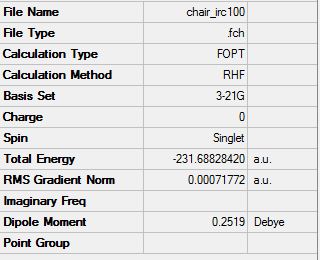
(iii) Compute force constants at every step
This method involved computing force constants at every step. This is the most reliable method that can be used, however this method may not work for larger systems as it will take a long time.

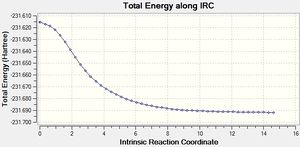
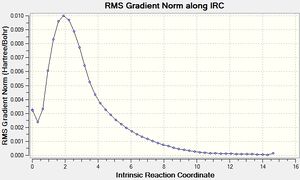
The above graphs show the points along the energy curve until the minimum was reached. However on the graph about the gradient, a slight incline is seen at the last point. This could correlate to the fact that the physical representation of a bond is removed between the 47th and 48th point. This may lead to a slight increase in energy towards the end of the curve. The energy for this method (-231.69166 Hartrees) is roughly similar to the energy obtained in method (i) (-231.69167) which suggests that a similar minimum has been achieved whereas the IRC and method (ii) produced a different minimum.
Boat
A similar method was carried out on the Boat conformer in an aim to reach the local minimum. From these calculations it can be seen that the minimum geometries from the transition states have been reached. Some methods were more successful than others and this is due to the fact that some methods can side-track on their structure if it is not similar to the minimum you are aiming to find.
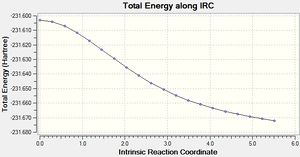
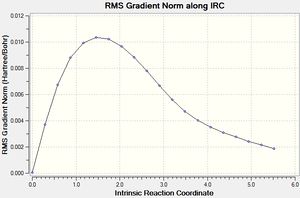
From the above graph it can be seen that the intermediate geometries are tending towards a minimum energy and a gradient which is closer to zero. The resulting structure has an energy of -231.67203 Hartrees.
IRC Opt
(i) The last point of the IRC is minimised
The final structure of the IRC was optimised using Hartree-Fock method and 3-21G basis set to give the structure below. This method resulted in a more stable structure.
(ii) Increasing the number of points on the IRC
Another IRC was carried out on the Boast transition structure, however the number of points was increased to 100, this did not result in a lower geometry structure as the calculation was completed in the same number of steps and the final structure had the same conformation and energy as the initial IRC that was run.
(iii) Compute force constants at every step
Re-running the IRC using force constants at every step is another method of calculating the minimum geometry.
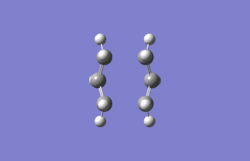


The above graph is interesting as there is a slight increase in gradient seen, which shows that there is a deviation from the minimum structure.
Comparing Boat and Chair Transition Structures
Below is a comparison of the Boat and Chair Transition structures calculated using the ICR method above:
| (Hartrees) | Chair | Boat |
| IRC | -231.68828 | -231.67203 |
| IRC(final optimised) | -231.69167 | -231.68300 |
| IRC (100 points) | -231.68828 | -231.7203 |
| IRC (force constants) | -231.69166 | -231.68562 |
From the table above it can be concluded that the chair transition state conformer is more stable than the boat transition structure. This is due to the internal steric repulsions felt. The table above also shows that the additional optimisations significantly optimised the transition structure, with the most effective methods being:
- Optimising the final point (method (i)) for the chair (2.13 kcal/mol difference)
- IRC including force constants (method (iii)) for the boat structure (8.53 kcal/mol difference)
Activation energy
Further activation energy calculations were carried out by optimising the transition structures to a TS (Berny) using B3LYP method with a 6-31G* basis set. The Thermochemistry data was then taken from the output files of these molecules and compared to the Anti2 (Ci) conformation to show the energy required to get from the reactant to the transition state. The full analysis of this can be seen in the table below.
Boat structure: DOI:10042/to-12578 Chair structure: DOI:10042/to-12582
| B3LYP/6-31G* (Hartrees) | Anti2(Ci) | Boat TS | Chair TS | Difference (boat) (kcal/mol) | Difference (chair) (kcal/mol) |
| Total Energy | -234.62319 | -234.55445 | -234.56752 | 43.14 | 34.93 |
| Zero-point energy | -234.41064 | -234.414235 | -234.425905 | 2.26 | 9.58 |
| Thermal energies | -234.4737 | -234.407819 | -234.419926 | 41.35 | 33.75 |
The values in the table above can be compares to experimental values: 33.5 ± 0.5 kcal/mol via the chair transition structure and 44.7 ± 2.0 kcal/mol via the boat transition structure at 0 K. The calculated energies match the literature values therefore showing that the chair transition structure has a lower activation energy therefore the reaction will proceed via this route.
Diels Alder Cycloaddition reaction
The Diels Alder Cycloaddition reaction is known as a type of pericyclic reaction between a diene and a dienophile to form a cyclohexene system. The π orbitals on the dienophile form new σ bonds with the π orbital from the diene. Usually if the HOMO of one interacts with the LUMO of the other than the cycloaddition is allowed, however both molecular orbitals need to have the same symmetry otherwise there will be no overlap and therefore the reaction will not proceed. The Cis principle [1] states that the stereochemistry of the reactants is maintained in the product and therefore the subsituents will be on the same face of the ring in the product. The maleic anhydride example below shows this, however the cis substituents are part of a ring and are therefore on the same face due to steric lock.
Butadiene and Ethylene
Butadiene and Ethylene can undergo a [4+2]- Cycloaddition to form cyclohexene. The reaction involves the interaction between the HOMO and LUMO's of Butadiene and Ethylene as seen below.
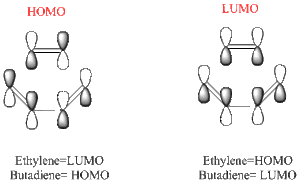
These LCAO's represent the interaction between the π and π* orbitals of the reactants. The Molecular orbitals obtained from the calculations will prove these interactions.
Optimising butadiene
A molecule of butadiene was drawn in GaussView and optimised using the Semi-empirical molecular orbital method with the AM1 basis set. Cis butadiene is used to ensure maximum orbital overlap is achieved.
HOMO- LUMO
| MO | Image | LCAO | Symmetry |
| HOMO |  |
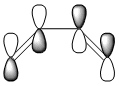 |
anti-symmetric |
| LUMO | 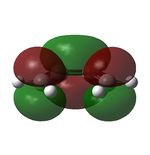 |
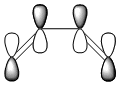 |
symmetric |
Transition State geometry
The ethylene approaches the cis butadiene from above, in an aim to maximum the overlap between the π orbitals.
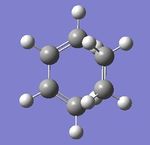
The bond lengths visible in the Jmol above shows the σ bond lengths of the partially formed C-C bonds. The typical Csp3-sp3 in cyclohexane is 1.535Å[2], and the typical Csp2-Csp2 bond length is 1.455[2]. Therefore it can be seen that the partially formed σ bond is much longer than both of these lengths as it is not yet a bond, however once formed it will relate most to the Csp3-sp3 length. The Van der Waals radius for carbon is 1.7Å[3], therefore it can be deduced that the distance is shorter than a Van der Waals interaction but not close enough to be a σ bond, therefore an intermediate stage has been reached.
The optimised transition state had an imaginary frequency at -956.14cm-1, this relates to the formation of the new σ-bonds which is synchronous.

This can then be compared tot he frequency of the lowest positive vibration at 147.29cm-1, which shows an asynchronous movement and does not relate to the formation of the new σ bonds.

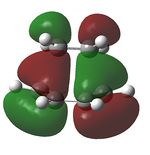
HOMO-LUMO
| HOMO | LUMO |
 |
 |
| Anti-symmetric | Symmetric |
The above diagrams show a molecular orbital representation of the π/ π* interaction of ethylene and the HOMO/LUMO of butadiene. The reaction is [4s + 2s] due to the fact that butadiene has 4 π orbitals in the π system and ehtylene has 2 π orbitals. The molecular orbitals of ethylene and butadiene have been labelled as symmetric and anti-symmetric with respect to the middle plane. The reason this reaction is allowed is because the HOMO of one interacts with the LUMO of the other, therefore it can be seen that the molecular orbitals of the transition state match the LCAO's predicted before the calculations were carried out.
Cyclohexa-1,3-diene reaction with Maleic Anhydride
This exercise aims to prove the fact that the cycloaddition reaction between cyclohexa-1,3-diene and maleic anhydride results in the primarily formation of the endo structure. This is due to the fact that the endo structure is lower in energy therefore the reaction is kinetically controlled resulting in a regioselective reaction.
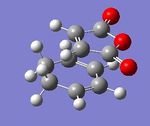
Exo Tranition structure
The exo and endo structures were calculated using the freeze coordination method. The cyclohexa-1,3-diene were optimised separately and then a guess structure of the transition state was made. The distance between the two carbons forming the new bonds were frozen at 2.2Å and then optimised using HF/3-21G. This step allows the rest of the atoms to relax whilst freezing the reacting carbons in their place.
The output file of this structure was optimised further by using derivate bonds, thus allowing them to move to form the optimum transition structure:
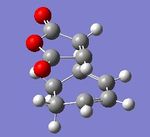
This structure also displayed an imaginary frequency at -647.42cm-1 with an intensity of 67.5. From the animation below it can be seen that this vibration links directly to the formation of the new σ-bonds.
| HOMO | LUMO |
 |
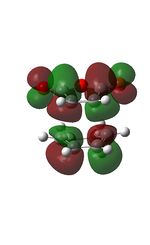 |
Endo Transition structure
The endo transition structure was calculated using the same method as the exo structure.
| HOMO | LUMO |
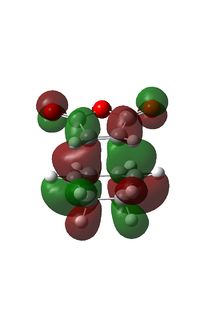 |
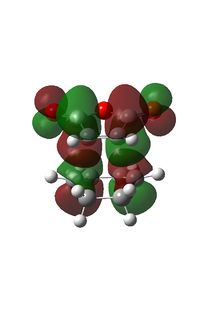 |
Comparison between endo and exo transition states
| exo | endo | |
| Method | HF/3-21G | HF/3-21G |
| Energy (Hartrees) | -605.60352 | -605.61037 |
From the above table it can be seen that the endo structure is more stable as it is lower in energy by 0.00685 Hartrees (4.3 Kcal/mol). This agrees with the statement made at the state that the endo structure was predominately formed due to the fact that the reaction proceeded due to kinetics.
The exo structure is higher in energy due to the strain between the carbonyl cabons and the cyclohexa-1,3-diene ring, which are 2.92Å apart. The steric disterence in the endo structure is much closer at 2.8Å, this may lead one to assume that the endo structure is not favored.
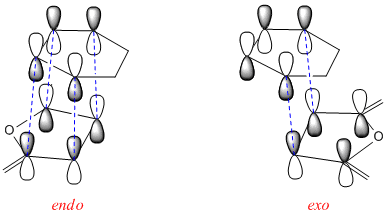
However, this reaction is not controlled by such sterics. The main factor that controls the stereochemistry is the secondary orbital interaction[4]. From the MO's above it can be seen that there is significantly more secondary orbital overlap in the endo structure compared to the exo structure. The LCAO's below show the extent overlap in a much clearer way. The increase in overlap in the HOMO stabilises the endo structure.
References
- ↑ J. Sauer, Diels-Alder reactions II: The reaction mechanism, 1967, 17, DOI:10.1002/anie.196700161
- ↑ 2.0 2.1 Frank H. Allen, Olga Kennard and David G. Watson, J. Chem. Soc. Perkin Trans. II, 1987, S6-S7
- ↑ A. Bondi, J. Phys. Chem., 1964, 448, DOI:10.1021/j100785a001
- ↑ Maryne Anne Fox, Raul Cardona, Nicoline J. Kiwiet, Journal of Organic Chemistry, 1987, 1469-1470, DOI:10.1021/jo00384a016