Rep:Mod:Ab mod2
Bonding (Ab initio and density functional molecular orbital)
Introduction
Computational methods can be used in Inorganic chemistry to carry out calculations on metal complexes which contain unusual bonding. The benefits of using such a program is that the Molecular orbitals, IR, Natural Bond Order and relative energies can be calculated and used to confirm the structure of the metal complex. First the structure needs to be optimised, the program is able to do this by taking the gradients until it becomes zero and the calculations converge, therefore a minimum is said to have been found.
The program used in this exercise was GaussView and additional more complex calculations were carried out on the HPC computing service. GaussView carries out the calculations by using the Schrodinger equation to work out the electron density whilst the nucleus is stationary, after which the nucleus is moved and the calculations are carried out again. The method and basis set used is changed according to the type of molecule being examined.
BH3
Optimisation
A molecule of BH3 was made in GuassView and bond lengths were changed to 1.5Å. The molecule was optimised used the B3LYP method and 3-21G basis set. A low accuracy basis set was used to allow the calculations to be carried out quickly.
From this optimisation we were able to determine that the nucleus is in an optimum position relative to the electronic structure based on the details below which show that the calculations have a gradient of zero and that it has converged i.e. for a small displacement the energy does not change.
Item Value Threshold Converged? Maximum Force 0.000090 0.000450 YES RMS Force 0.000059 0.000300 YES Maximum Displacement 0.000352 0.001800 YES RMS Displacement 0.000230 0.001200 YES Predicted change in Energy=-4.580970D-08 Optimization completed. -- Stationary point found.
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1945 -DE/DX = -0.0001 !
! R2 R(1,3) 1.1945 -DE/DX = -0.0001 !
! R3 R(1,4) 1.1945 -DE/DX = -0.0001 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The four pictures of BH3 below show what the molecule looks like at different iterations on the graph. The final point being the optimised molecule as a gradient close to zero can be seen and the energy is the lowest. This is the equilibrium molecule which is represented by the minimum in a potential energy vs. bond distance graph.
The first two molecule shows no bonds between the Boron and Hydrogens and this is because Gaussian draws bonds based on distance, therefore there are bonds present but the distance is larger than the pre-defined value and hence not shown. Bonds are defined by the sharing of electronic density and not by the physical drawing of a bond (See 'What is a bond?' below).
Vibrational Analysis
Using the optimised BH3 molecule, further frequency calculations were carried out. The key point in this step is to determine if the minima has been reached. If all the frequencies are positive then a minimum has been reached, if one is negative then a transition state has been achieved, however if there is more than one negative frequency than the optimisation has failed.
Low frequencies --- -0.3716 -0.0098 -0.0018 37.2444 37.9574 37.9592 Low frequencies --- 1146.0292 1204.8631 1204.8641
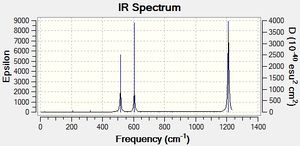
The predicted IR spectrum for BH3 shows six different vibrations, these are listed in the table below:
| Mode No. | Form of Vibration | Image | Frequency/cm-1 | Intensity | Description | Symmetry |
| 1 | Hydrogens wagging in and out of plane |  |
1146.03 | 92.7 | Stationary Boron atom is stationary whilst the Hydrogens move in and out of the plane simultaneously. | A2" |
| 2 | Scissoring |  |
1204.86 | 12.4 | The two hydrogens move down whilst the boron and hydrogen remain stationary. 2 bond angles are increased whilst one is constricted. | E' |
| 3 | Rocking |  |
1204.86 | 12.4 | One hydrogen ungergoes large movement thus increasing one angle and decreasing another whilst the other two hydrogens move slightly to maintain the third angle. | E' |
| 4 | Symmetrical stretching |  |
2591.65 | 0 | All Boron- Hydrogen bonds stretch simultaneously. Symmetrical stretching. | A1' |
| 5 | Asymmetric stretch |  |
2730.07 | 103.9 | Two Boron-Hydrogen bonds increase and decrease assymetrically whilst one B-H stays constant. | E' |
| 6 | Asymmetric stretch |  |
2730.07 | 103.8 | Two B-H bonds stretch symmetrically whilst the third bond stretches asymmetrically | E' |
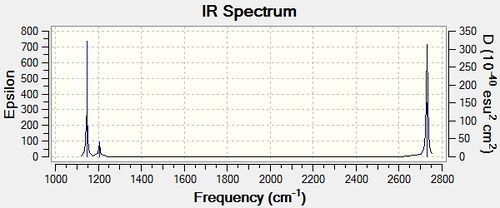
Six vibrational modes are described, however the above IR spectrum only shows three peaks. The reason for this is because the E' type vibrations are degenerate and therefore only show up as one peak. Additionally, frequency mode four has a symmetrical stretch and therefore no change in dipole moment happens therefore no peak is seen.
Molecular Orbitals
The optimised BH3 molecule was used to carry out molecular orbital analysis. The molecule was scanned on the HTC ( DOI:10042/to-11994 ) using the 'energy' method with 'full NBO'. The resulting checkpoint file was opened in GuassView and the lowest eight Molecular orbitals were viewed, a summary of which can be seen below:
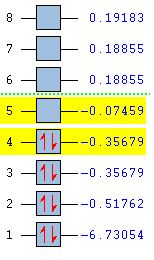
The 4th MO is the HOMO and the 5th MO is the LUMO. As you look at higher energy unoccupied orbitals they become more diffuse than the occupied ones.
An MO for a trigonal planar D3h BH3 molecule was drawn up and compared to the LCAO MO's. Boron is more electropositive and is therefore slightly higher in energy than the H3 fragment. A diagram for the complete MO can be seen below:
The order of the top two orbitals is complex and changes depending on the molecule used to carry out the calculations. The above diagram shows that the s-s antibonding interactions are less favourable and thus higher in energy, however the original H3 and Boron a1' orbitals are lower in energy than the e' orbitals so one might assume that they would be lower in energy than the e' orbitals. However the exact position of these two orbitals can not be determined by computational methods alone.
From the above MO we can determine the accuracy and usefulness of qualitative MO theory. The predicted LCAO orbitals were placed next to the computed MO's for ease of comparison. There is a good match between the LCAO's and the computed MO's which shows that computational methods are a useful for predicting MO's for small molecules, if bigger molecules wanted to be calculated then the method would have to be changed to deal with the increase in electron density.
NBO Analysis
Using the optimised BH3 molecule, the charge distribution can be seen. Green indicates highly positive charge and the red colour represents a highly negative charge. From the image below it can be deduced that the Boron is electron deficient and thus highly positively charged.
The Summary below shows the Natural charges of the atoms, Boron being positive and the Hydrogen's being negative.
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.33161 1.99903 2.66935 0.00000 4.66839
H 2 -0.11054 0.00000 1.11021 0.00032 1.11054
H 3 -0.11054 0.00000 1.11021 0.00032 1.11054
H 4 -0.11054 0.00000 1.11021 0.00032 1.11054
=======================================================================
* Total * 0.00000 1.99903 6.00000 0.00097 8.00000
The below output data shows the type of bonding present in the molecule.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99853) BD ( 1) B 1 - H 2
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 2 s(100.00%)
1.0000 0.0000
2. (1.99853) BD ( 1) B 1 - H 3
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 3 s(100.00%)
1.0000 0.0000
3. (1.99853) BD ( 1) B 1 - H 4
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 4 s(100.00%)
1.0000 0.0000
4. (1.99903) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
The first data entry shows the bonding (BD) present between the boron and one hydrogen. The boron contributes 44.48% of it's orbital and the hydrogen contributes 55.52% towards the bond. The boron is sp2 hybridised with 33.33% s character and 66.67% p character. The hydrogen is 100% s character. Data entries two and three both show similar distribution. The forth data entry (CR) shows the core of the 1s orbital on Boron and the fifth data entry shows the lone pair on the Boron.
Second order perturbation theory shows the interaction of bonding NBOs with non-bonding NBOs. However from the table below it can be seen that the E(2) column doesn't contain any data points above 20kcal/mol, therefore there is little information available from this for a small molecule like BH3.
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
within unit 1
4. CR ( 1) B 1 / 10. RY*( 1) H 2 1.51 7.54 0.095
4. CR ( 1) B 1 / 11. RY*( 1) H 3 1.51 7.54 0.095
4. CR ( 1) B 1 / 12. RY*( 1) H 4 1.51 7.54 0.095
The Summary below shows the the occupancy and energy of the B-H bonds (BD) as well as the Boron lone pairs (LP).
Natural Bond Orbitals (Summary):
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (H3B)
1. BD ( 1) B 1 - H 2 1.99853 -0.43712
2. BD ( 1) B 1 - H 3 1.99853 -0.43712
3. BD ( 1) B 1 - H 4 1.99853 -0.43712
4. CR ( 1) B 1 1.99903 -6.64476 10(v),11(v),12(v)
5. LP*( 1) B 1 0.00000 0.67666
6. RY*( 1) B 1 0.00000 0.37177
7. RY*( 2) B 1 0.00000 0.37177
8. RY*( 3) B 1 0.00000 -0.04532
9. RY*( 4) B 1 0.00000 0.43446
10. RY*( 1) H 2 0.00032 0.90016
11. RY*( 1) H 3 0.00032 0.90016
12. RY*( 1) H 4 0.00032 0.90016
13. BD*( 1) B 1 - H 2 0.00147 0.41201
14. BD*( 1) B 1 - H 3 0.00147 0.41201
15. BD*( 1) B 1 - H 4 0.00147 0.41201
-------------------------------
Total Lewis 7.99463 ( 99.9329%)
Valence non-Lewis 0.00441 ( 0.0551%)
Rydberg non-Lewis 0.00097 ( 0.0121%)
-------------------------------
Total unit 1 8.00000 (100.0000%)
Charge unit 1 0.00000
TlBr3
A trigonal planar molecule of TlBr3 was made in GuassView and used to analysis the use of Pseudo-potentials and larger basis sets than previously used in the BH3 exercise.
Optimisation
Before optimising the TlBr3 molecule, the point group was restricted to D3h with a tolerance of 'Very tight (0.0001). This is to ensure that the molecule has the correct symmetry needed for analysing the MOs and vibrations.
Optimisation calculations were carried out using B3LYP with LanL2DZ basis set. A larger basis set has to be used to account for the heavier second row element and pseudo-potentials can be used to make the calculations more manageable.
Log file of optimised TlBr3: https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:TLBR3OPT3_ab.LOG
Item Value Threshold Converged? Maximum Force 0.000002 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000022 0.001800 YES RMS Displacement 0.000014 0.001200 YES Predicted change in Energy=-6.082801D-11 Optimization completed. -- Stationary point found.
From the above summary and data file it can be seen that the molecule has been successfully optimised because the gradient is close to zero therefore the minima has been found and the calculations have successfully converged.
The optimised molecule shows a Tl-Br bond length of 2.65Å and an optimised Br-Tl-Br bond angle of 120°. These values are in good agreement with the literature value[1] for the Tl-Br bond length of 2.6182Å.
Frequency Analysis
Frequency calculations need to be carried out to determine if the minima has been reached. If negative frequencies are seen then either a transition state is reached (one negative value) or the minimum hasn't been reached (many negative frequencies values).
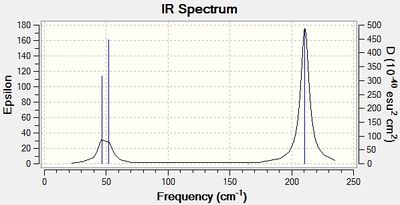
| Mode no. | Frequency/cm-1 | Intensity | Image |
| 1 | 46.4 | 3.7 |  |
| 2 | 46.4 | 3.7 |  |
| 3 | 52.1 | 5.8 |  |
| 4 | 165.3 | 0 |  |
| 5 | 210.7 | 25.5 |  |
| 6 | 210.7 | 25.5 |  |
Below are the low frequencies that were found in the original log file ( DOI:10042/to-11996 ):
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367 Low frequencies --- 46.4289 46.4292 52.1449
The 'low frequencies' above are the motions of the center of mass of the molecule. Therefore these need to be lower than the first vibration or within plus or minus 10cm-1. The 'low frequencies' above fit into this criteria.
What is a bond?
When a molecule is optimised in GaussView, the bonds between atoms may not been seen. This is because GaussView has a list of pre-defined bond lengths and if a bond is longer than this then the program does not show a physical bond drawn. However this does not mean that a bond is not present, in fact the bonds are present but due to the fact that inorganic molecules contain longer bonds than the pre-defined values, they are not seen.
A bond can be characterised as one of three main types[2]: ionic, covalent or metallic. An ionic bond is the transfer of electrons resulting in an attraction of oppositely charged atoms. A covalent bond is when electrons of similar valence orbital energies combine to form a bond between two atoms. And a metallic bond can be defined by the delocalisation of electrons between positively charged nuclei.
Isomers of Mo(CO)4L2
The symmetry of Mo(CO)4L2 complexes can be deduced from the vibrational spectrum. The number of CO vibrational bands is directly related to the symmetry of the molecule, the cis isomer displays four carbonyl bands whereas the trans isomer displays one carbonyl peak. The difference in structure of the two molecules can be seen below (dihedral angles set):
The phenyl rings on the phosphorus have been replaced with chlorine atoms which have the same electronic contribution and are as sterically demanding as the phenyl groups.
Optimisation
An initial optimisation was carried out using the B3LYP method and the pseudo-potential LANL2MB (minimum basis) to give the following molecules which are roughly optimised structures:
Jmol for the LANL2MB Cis Isomer ( DOI:10042/to-12004 )
Jmol for the LANL2MB Trans Isomer ( DOI:10042/to-12003 )
Using the LANL2MB method:
However the above molecules are not the lowest energy minima, this is because the PCl3 groups can freely rotate. Therefore to ensure the correct minima is found; the one with the lowest energy. The dihedral angle for the cis isomer was set to either 0° or 180° depending on which Cl was being set. The trans isomer was adjusted so that when you look down the P-Mo-P bond the Cl's all eclipsed (see Jmol below).
A further optimisation was carried out using the B3LYP method with the LANL2DZ pseudo-potential, this basis set and pseudo-potential allows a tighter convergence.
Jmol for the LANL2DZ Cis Isomer ( DOI:10042/to-12006 )
Jmol for the LANL2DZ Cis Isomer ( DOI:10042/to-12005 )
Using the LANL2DZ method:
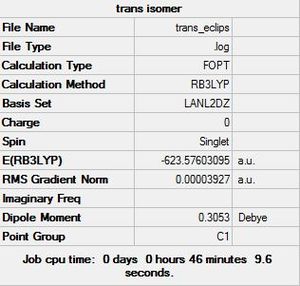
From the above summary tables it can be deduced that the trans isomer is the most thermodynamically stable isomer by 2.73kJ/mol. This is a relatively small energy barrier and can be overcome by heating and once heated the trans-isomer will dominate. This supports the evidence[3] that the cis isomer would isomerise to form the trans isomer when the temperature was increased, thus it can be deduced that the cis isomer is the kinetic isomer and the trans isomer is the thermodynamic isomer.
Computational methods can be used to determine how to stabilise structures and hence 'fine-tune' them towards catalytic behavior. In the current conditions examined above the trans isomer is the more stable structure compared to the cis isomer, if one wanted to change this to make the cis isomer more stable then they would change the R substituents on the PR3 group to something which can stabilise the R groups on the PR3 group cis to it, an example of this might be a group which hydrogen bonds or has strong dipole or Van der Waals interactions.
Comparison of Cis and Trans geometries to literature
| Cis-Isomer | Calculated bond lengths (Å) | Literature values[4] |
| Mo-C | 2.06 | 2.04 |
| C-O | 1.17 | - |
| Mo-P | 2.51 | 2.48 |
| P-Cl | 2.24 | - |
| Trans-Isomer | Calculated bond lengths (Å) | Literature values[4] |
| Mo-C | 2.06 | 2.16 |
| C-O | 1.17 | - |
| Mo-P | 2.44 | 2.41 |
| P-Cl | 2.24 | - |
From the above tables it can be seen that there is good agreement between the calculated bond distances and the values found in literature. The literature values differ slightly because the exact same molecule was not found therefore a similar molecule (Mo(CO)4(PH3)2) had to be used to allow comparison.
The cis isomer has a longer Mo-P bond length than the trans isomer, this is due to the fact that the cis isomer faces steric clash between the large PCl3 groups being close together therefore the Mo-P appears to be longer in an effort to relieve some of the steric strain.
Frequency Analysis
Frequency analysis was carried out on the optimised molecules using the B3LYP method, pseudo-potential LANL2DZ with additional key words 'int=ultrafine scf=conver=9'. No negative frequencies were observed, therefore it can be deduced that the correct minima was reached.
Optimised Cis Isomer IR spectrum ( DOI:10042/to-12007 ):
Optimised Trans Isomer IR spectrum ( DOI:10042/to-12008 ):
Vibrational analysis
Carbonyl stretches
Cis Isomer carbonyl stretches are shown below:
The Frequencies below are compared to that of Mo(CO)4PPh3, which is similar to the molecule we are investigating in many ways.
| Mode no. | Frequency(cm-1) | Intensity | Literature Frequency(cm-1)[3] | Image | Symmetry |
| 42 | 1945.2 | 763 | 1897 |  |
B2 |
| 43 | 1948.6 | 1498 | 1908 |  |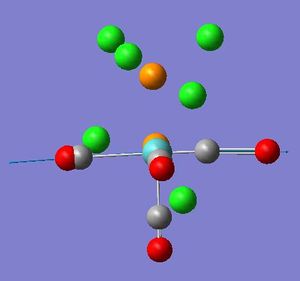
B1 |
| 44 | 1958.3 | 633 | 1927 |  |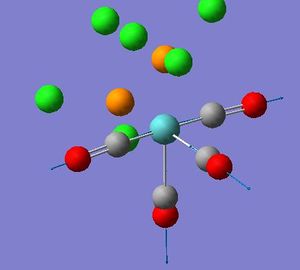
A1 |
| 45 | 2023.2 | 598 | 2023 |  |
A1 |
The above table shows that there are four distinct IR stretches for the carbonyl groups. Each vibration is visible on the IR spectrum as individual peaks. Four peaks confirms that the molecule is the cis isomer.
Trans Isomer carbonyl stretches are shown below:
The below frequencies are compared to Mo(CO)4(PnBu3)2.
| Mode no. | Frequency(cm-1) | Intensity | Literature Frequency(cm-1)[3]' | Image | Symmetry |
| 42 | 1950.5 | 1475 | 1885.4 |  |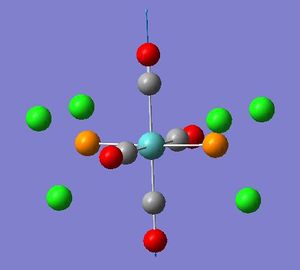
Eu |
| 43 | 1951.1 | 1467 | 1885.4 |  |
Eu |
| 44 | 1977.5 | 1 | - |  |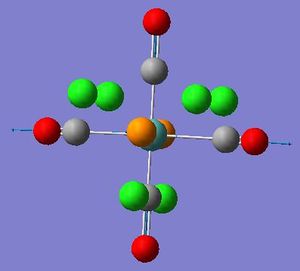
B1g |
| 45 | 2031.2 | 4 | - |  |
A1g |
The trans isomer only shows up as one peak on the IR spectrum. This is because the frequency modes 42 and 43 are degenerate and similar in frequency therefore show in one peak. Vibrational modes B1g and A1g would not be seen on the IR spectrum because they undergo a symmetrical stretch and therefore there is no change in dipole, however the above data shows that they are visible at low intensity, this is because of the deviation in perfect 90° angles.
Low frequencies
Cis Isomer
| Freq. Mode No. | Freq | Intensity |
| 1 | 10.93 | 0.02 |
| 2 | 17.71 | 0.01 |
Trans Isomer
| Freq. Mode No. | Freq | Intensity |
| 1 | 4.84 | 0.09 |
| 2 | 6.13 | 0 |
Mini Project
This project will investigate the difference between phosphazenes rings when the substituent is changed from H to Cl and F. The main computational method that will be used to determine the affect of changing the substituent is the NBO calculations.
Delocalisation in the ring occurs from the overlap of (P)dπ-(N)pπ orbitals. The σ framework is built up from an N sp2 hybridised orbital and a sp3 P orbital. A 'non-bonding' sp2 on Nitrogen is occupied with a lone pair whilst the pz is able to further π-interact with the dxy and dyz orbitals of Phosphorus.
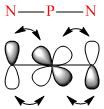
Comparing the bond lengths will allow us to compare the extent of the overlap when the substitutent is changed. Fluorine is the most electron donating substituent in these examples, therefore it is able to push more electron density onto the Phosphorus which will allow further interaction and delocalisation onto the nitrogen's.
Optimisation
GuassView was used to draw each molecule in turn. A benzene template was used and the substituents were changed from carbons to nitrogens and phosphorus atoms. The differences between the three structures are the X substituents on the Phosphorus, they are changed from H to F to Cl. Each optimisation was carried out using the B3LYP method and the pseudo-potential 6-31G(d). Below is a summary of each optimisation carried out. Each optimisation was successful because the final gradient was close to zero and the data output file shows the the molecule converged. Bond lengths and angles were taken and compared to literature values[5] to see the accuracy of the calculations, good agreement was found for most bond lengths and angles. Differences between calculated and literature values is due to the slight change in configuration when optimising.
H substituted
The optimised structure of the H-substituted phosphazene ring: DOI:10042/to-12132
Item Value Threshold Converged? Maximum Force 0.000057 0.000450 YES RMS Force 0.000031 0.000300 YES Maximum Displacement 0.000315 0.001800 YES RMS Displacement 0.000155 0.001200 YES Predicted change in Energy=-1.158864D-07 Optimization completed. -- Stationary point found.
| (PNH2)3 | Calculated | Literature |
| P-N | 1.617 | 1.616 |
| P-H | 1.412 | 1.413 |
| P-N-P | 121.4 | 121.3 |
| N-P-N | 118.6 | 118.7 |
| H-P-H | 101.1 | 100.6 |
F substituted
The log file for the optimised phosphazene ring with fluorine substitutents is available on: DOI:10042/to-12138
Item Value Threshold Converged? Maximum Force 0.000303 0.000450 YES RMS Force 0.000076 0.000300 YES Maximum Displacement 0.000570 0.001800 YES RMS Displacement 0.000193 0.001200 YES Predicted change in Energy=-2.337502D-07 Optimization completed. -- Stationary point found.
| (PNF2)3 | Calculated | Literature |
| P-N | 1.589 | 1.691 |
| P-F | 1.57 | 1.675 |
| P-N-P | 121 | 121.2 |
| N-P-N | 118.9 | 118.9 |
| F-P-F | 97.9 | 97.2 |
Cl substituted
The optimised molecule: DOI:10042/to-12137
Item Value Threshold Converged? Maximum Force 0.000294 0.000450 YES RMS Force 0.000081 0.000300 YES Maximum Displacement 0.000862 0.001800 YES RMS Displacement 0.000396 0.001200 YES Predicted change in Energy=-2.812321D-07 Optimization completed. -- Stationary point found.
| (PNCl2)3 | Calculated | Literature |
| P-N | 1.6 | 1.719 |
| P-Cl | 2.04 | 2.189 |
| P-N-P | 121.7 | 118.1 |
| N-P-N | 118.3 | 121.84 |
| Cl-P-Cl | 102.1 | 102.3 |
Comparison
The above bond lengths can be compared to show the extent of orbital overlap and delocalisation that occurs when the substituents are changed. The shortest bond length is seen when the substituent is fluorine. This shows that the fluorine is able to push more electron density onto the phosphorus thus allowing more overlap and therefore a shorter bond distance. This bond distance observed is shorter than the bond distance observed for the phosphazene with hydrogen as the substituent, therefore it can be concluded that more than a single bond is present between the phosphorus and nitrogen.
The fluorine substituted complex seems to have the lowest energy due to the stabilisation of the structure through the electron donating ability of the fluorine. Fluorine is the most electronegative therefore one may assume that is would be electron-withdrawing, however when fluorine is a substituent on an aromatic ring it is able to electron donate into the ring and contribute to the delocalisation.
The chlorine substituted phozphazene shows longer bond P-X bond lengths and larger angles compared to the fluorine and hyrogen complexes. This is because chlorine is a lot larger than fluorine and hydrogen, therefore the bonds are longer. Additionally there are more electrons to account for in the calculations, therefore to improve on this a higher basis set could have been used but this would have taken a lot longer.
All P-N bonds seen above are a lot smaller than you would expect to see in a singly P-N bound molecule (H3N-PO3)-, which have a bond length of 1.77Å[6]. Therefore, it can be deduced that they are more strongly bound than a single σ bond.
NBO Analysis
H substituted
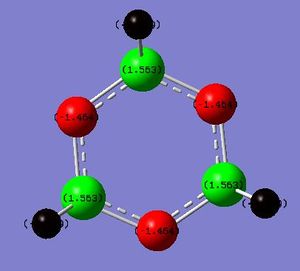
Bonding between P and Nitrogen:
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98138) BD ( 1) N 1 - P 4
( 70.65%) 0.8405* N 1 s( 33.63%)p 1.97( 66.16%)d 0.01( 0.22%)
-0.0002 0.5799 0.0025 0.0005 -0.0019
-0.7056 -0.0268 0.0039 -0.4036 -0.0048
0.0104 0.0000 0.0000 0.0000 0.0380
0.0000 0.0000 0.0023 -0.0265
( 29.35%) 0.5418* P 4 s( 26.83%)p 2.67( 71.74%)d 0.05( 1.43%)
0.0000 0.0002 0.5173 -0.0264 -0.0026
0.0004 0.0002 0.7621 -0.0109 0.0002
0.0002 0.3666 -0.0464 -0.0047 0.0000
0.0000 0.0000 0.0000 0.0819 0.0000
0.0000 0.0682 -0.0538
The above information shows us that the Nitrogen contributes 70.65% towards the bond whereas the phosphorus contributes 29.35%. Thus the majority of the bond is formed by the electron density on the Nitrogen.
Bonding between Phosphorus and Hydrogen substituent:
7. (1.97490) BD ( 1) P 4 - H 5
( 49.88%) 0.7063* P 4 s( 23.26%)p 3.24( 75.30%)d 0.06( 1.45%)
0.0000 -0.0004 0.4819 0.0182 0.0015
-0.0005 -0.0002 -0.4448 -0.0058 -0.0033
0.0001 0.2568 0.0034 0.0019 0.0000
0.6992 -0.0156 0.0033 -0.0342 -0.0903
0.0522 0.0197 0.0449
( 50.12%) 0.7079* H 5 s(100.00%)
0.9999 0.0117
F substituted
Bonding between P and N:
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.96631) BD ( 1) N 1 - P 4
( 72.45%) 0.8512* N 1 s( 33.07%)p 2.02( 66.64%)d 0.01( 0.29%)
0.0005 -0.5750 -0.0013 0.0011 0.0006
0.8162 0.0067 0.0016 0.0027 -0.0115
-0.0012 0.0000 0.0000 0.0000 -0.0210
0.0000 0.0000 -0.0393 0.0304
( 27.55%) 0.5249* P 4 s( 29.24%)p 2.36( 68.96%)d 0.06( 1.80%)
0.0000 -0.0002 -0.5404 -0.0101 -0.0148
0.0016 -0.0002 -0.8276 -0.0453 0.0104
-0.0001 0.0410 -0.0237 -0.0162 0.0000
0.0000 0.0000 0.0000 0.0217 0.0000
0.0000 -0.1172 0.0617
Bonding between P and F:
10. (1.92853) BD ( 1) P 4 - F 9
( 15.08%) 0.3884* P 4 s( 20.83%)p 2.57( 53.45%)d 1.23( 25.72%)
0.0000 -0.0005 0.4558 -0.0118 -0.0219
0.0003 -0.0001 -0.2670 -0.0111 0.0116
0.0001 0.4624 0.0192 -0.0200 -0.0003
0.4720 0.1338 -0.0874 -0.0432 -0.3760
0.3320 -0.0249 0.0552
( 84.92%) 0.9215* F 9 s( 27.41%)p 2.64( 72.46%)d 0.00( 0.13%)
0.0000 0.5235 -0.0029 -0.0049 -0.0028
0.2762 -0.0016 -0.0021 -0.4783 0.0028
0.0037 -0.6477 0.0069 0.0047 -0.0119
-0.0155 0.0268 -0.0068 0.0132
Cl substituted
Bonding between P and N:
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.96744) BD ( 1) N 1 - P 4
( 71.46%) 0.8453* N 1 s( 34.33%)p 1.90( 65.39%)d 0.01( 0.28%)
0.0005 -0.5859 0.0010 0.0064 0.0001
0.8084 0.0101 -0.0026 -0.0109 -0.0091
0.0009 0.0000 0.0000 0.0000 -0.0187
0.0000 0.0000 -0.0399 0.0289
( 28.54%) 0.5342* P 4 s( 29.70%)p 2.32( 68.97%)d 0.04( 1.32%)
0.0000 -0.0001 -0.5447 0.0155 -0.0057
-0.0044 -0.0002 -0.8282 0.0382 0.0141
-0.0002 0.0367 0.0279 -0.0109 0.0000
0.0000 0.0000 0.0000 0.0151 0.0000
0.0000 -0.1024 0.0503
Bonding between P and Cl:
10. (1.83615) BD ( 1) P 4 -Cl 9
( 30.33%) 0.5507* P 4 s( 20.33%)p 2.62( 53.33%)d 1.30( 26.35%)
0.0000 -0.0004 0.4506 0.0145 -0.0048
-0.0044 -0.0001 -0.2701 0.0078 0.0035
0.0002 0.4678 -0.0135 -0.0060 -0.0002
0.4557 -0.1682 -0.0724 -0.0416 -0.4014
0.3126 -0.0240 0.0483
( 69.67%) 0.8347*Cl 9 s( 14.03%)p 6.10( 85.55%)d 0.03( 0.42%)
0.0000 0.0001 0.3738 -0.0180 -0.0146
0.0014 0.0000 0.2806 -0.0073 0.0020
0.0000 -0.4856 0.0127 -0.0034 -0.0001
-0.7351 0.0194 -0.0027 -0.0182 -0.0270
0.0467 -0.0105 0.0290
Comparison of the three structures
| ' | H-substituted | Cl- substituted | F- substituted |
| P-N bond | - | - | - |
| N contribution | 70.65% | 71.46% | 72.45% |
| P contribution | 29.35% | 28.54% | 27.55% |
| P-X bond | - | - | - |
| P contribution | 49.88% | 30.33% | 15.08% |
| X contribution | 50.12% | 69.67% | 84.92% |
As the substituent becomes more electronegative (H<Cl<F), the contribution of atoms towards the bonds changes. The more electronegative the substituent is the more it able to contribute towards the P-X bond and hence the phosphorus is more tightly bound to the substituent. This allows the lone pair in the pz orbital of the nitrogen to overlap with the d-orbital of the phosphorus. This is evident by the electronic contribution of nitrogen in the P-N bond, the nitrogen contribution increases as the substituent on the phosphorus becomes more electronegative.
MO Analysis
The below diagrams show the LUMO to HOMO-3 Molecular orbitals for the three complexes. It is difficult to pull comparison between these molecular orbitals because the hydrogen substituted phosphazene would have fewer MO's as the hyrogen is only able to contribute through it's s orbital, whereas the bonding in the fluorine and chlorine substituted phosphazenes involve p orbitals as well (see NBO analysis above).
The fluorine LUMO is of the most interest as it shows a large area of delocalisation, this shows a reason for why the fluorine substituted complex is the most aromatic, as there is a large area of electron density distributed across the ring in the correct phase.
Vibrational Analysis
Frequency calculations were carried out on the molecules using the B3LYP method and the 6-31G (d) psuedo-potential. No negative frequencies were seen therefore it can be deduced that the minima was reached successfully.
H substituted
| Freq mode no. | Frequency | Intensity | Image |
| 3 | 114.2 | 36.7 |  |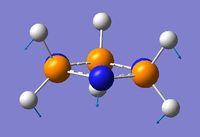
| 12 | 733.9 | 113.5 |  |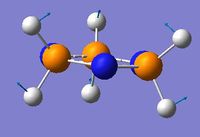
| 17 | 1138.2 | 475.2 |  |
| 19 | 1204.4 | 552.4 |  |
| 27 | 2441.1 | 350.8 |  |
| 28 | 2469.6 | 258.1 |  |
| 29 | 2469.6 | 258.1 |  |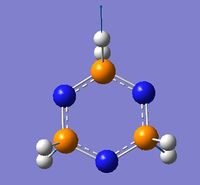
F substituted
| Freq mode no. | Frequency | Intensity | Image |
| 15 | 440.8 | 72 |  |
| 17 | 476.3 | 70 |  |
| 20 | 823.9 | 377.3 |  |
| 24 | 938.4 | 550.4 |  |
| 29 | 1282.3 | 896.7 |  |
Cl substituted
| Freq mode no. | Frequency | Intensity | Image |
| 19 | 514.8 | 322.4 |  |
| 23 | 604.8 | 591.7 |  |
| 29 | 1210 | 1204.2 |  |
References
- ↑ Handbook of Chemistry and Physics, 92nd edition, 2011-2012, Section 9-p.21,
- ↑ Harry B. Gray, Chemical Bonds: An intro to Atomic and Molecular Structure, 1994, 50,
- ↑ 3.0 3.1 3.2
Donald J Darensbourg,
Inorganic Chemistry,
1979,
18(1), pp.14-17,
Template:DOI: 10.1021/ic50191a003 Cite error: Invalid
<ref>tag; name "Donald" defined multiple times with different content - ↑ 4.0 4.1
C.Daniel, A.Veillard,
Inorganic Chemistry,
1989,
1173,
Template:DOI:10.1021/ic00305a029 Cite error: Invalid
<ref>tag; name "Daniel" defined multiple times with different content - ↑ Hassan Sabzyan, Zahra Kalantar, Journal of Molecular Structure (Theochem) 663, 2003, 151-155,
- ↑ D.W.J. Cruickshank, Acta Crystallogr 17, 1964, 671