Rep:Mod:AW611Phys

Module 3 (Y3C Physical)

The Cope Rearrangement

Introduction to the Cope Rearrangement

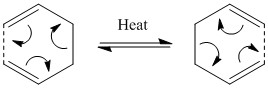
The Cope rearrangement involves the intramolecular pericyclic reaction of a 1,5 diene upon heating, discovered by Arthur Cope. The rearrangement is a [3,3] sigmatropic shift where an allyl group migrates. Since the reaction involves 6 electrons (4n+2) and occurs upon heating (Δ) the reaction proceeds suprafacially with Hückel topology according to the Woodward-Hoffman rules. If the rearrangement is of 1,5 hexadiene then the product is an isoenergetic regioisomer of the reactant, and therefore the equilibrium constants for both the forward and reverse reactions are equal. But, if the 1,5 diene conatins a substituent on the 3 or 4 position, the reaction produces a more substituted alkene product, which is consequently more thermodynamically stable, leading to the equilibrium constant of the forward reaction becoming much larger than that of the reverse reaction. Shown above is the rearrangement of 1,5 hexadiene. This rearrangement can proceed via one of two transition state, boat or chair, with the chair transition state predicted to be lower in energy.

In this experiment, computational methods were used to investigate the stability of the conformers of 1,5 hexadiene and to investigate the likely transition states, and their associated activation energies, for the Cope rearrangement. This could then be used to predict the likely path that the reaction takes.

Optimization and Analysis of the Reactants and Products

Antiperiplanar Conformer of 1,5 hexadiene

Firstly, a conformer of 1,5 hexadiene with an antiperiplanar linkage (dihedral angle=180^o for the 4 central C atoms) was drawn using GaussView. This structured was cleaned up and then optimised using the Hartree-Fock(HF) 3-21G method, then symmetrized to find the point group of the molecule.

3D model of the optimized anti conformation:

Anti 1,5 hexadiene

Table 1. Summary of anti 1,5 hexadiene data from optimization

File type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	singlet
Total Energy	-231.69260235 a.u.
Total Energy	-145,389.33408424 kcal/mol
RMS Gradient Norm	0.00001824 a.u.
Dipole Moment	0.2021 Debye
Point Group	C2

Gauche Conformer of 1,5 hexadiene

Again using GaussView 1,5 hexadiene was drawn out, however this time a gauche conformer was produced by changing the dihedral angle around the four central carbon atoms from 180^o to 60^o. This was then optimized using the HF 3-21G method, and symmetrized to give the point group of the conformer.

3D model of the optimized gauche conformer:

Gauche 1,5 hexadiene

Table 2. Summary of gauche 1,5 hexadiene optimization

File type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	singlet
Total Energy	-231.69166701 a.u.
Total Energy	-145,388.7471494 kcal/mol
RMS Gradient Norm	0.00001086 a.u.
Dipole Moment	0.3805 Debye
Point Group	C2

It was predicted that gauche would be higher in energy than the anti conformer due to greater steric hinderance, probably due to the clash of the alkene groups that are much closer together in the gauche conformer. From the data above and for that of the anti conformer, it is clear that the anti conformer is lower in energy, this is likely to be due to the greater steric hinderance in the gauche conformer. Using Appendix 1 of the script, it is clear that the conformers modelled were the Anti 1, and Gauche 2 conformers, due to the close agreement of energy values and point groups.

It is worth noting that these optimizations were carried out using a low level method HF 3-21G therefore discussion of relative energies of conformers is restricted by this, in future it may be worth checking these calculations using a higher level method.

Lowest Energy Conformer

There are actually 6 energetically distinct gauche conformers and 4 anti conformers, with the Gauche 3 conformer (with C₁ symmetry) being lowest in energy. Therefore the stability of conformers is contolled predominantly by the stereoelectronics rather than sterics. In the Gauche 3 conformation the donation of electron density from the π C=C orbital to the σ* C-H orbital is at it's greatest, due to more overlaps with C-H σ* than in the anti conformation, and there are also more favourable Van der Waals interaction between the hydrogens in this conformation compared to the anti (A^1,3 strain)

Anti 2 Conformer (C_i)

HF 3-21G Method

The anti 2 conformer was drawn out in GaussView and optimized using the HF 3-21G method, as above.

3D model of the HF 3-21G optmized anti 2 conformer:

Anti 2 1

Table 3. Summary of anti 2 1,5 hexadiene data from HF 3-21G optimization

File type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	singlet
Total Energy	-231.69253528 a.u.
Total Energy	-145,389.29199717 kcal/mol
RMS Gradient Norm	0.00001891 a.u.
Dipole Moment	0.0000 Debye
Point Group	Ci
C-C Bond Length	1.55 and 1.51Å
C=C Bond Length	1.32Å

B3LYP 6-31G^* Method

The already HF 3-21G optimised anti 2 conformer was then optimised again, this time using the B3LYP 6-31G^* method.

3D model of the B3LYP 6-31G^* optmized anti 2 conformer:

Anti 2 2

Table 4. Summary of anti 2 1,5 hexadiene data from HF 3-21G optimization

File type	.chk
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G*
Charge	0
Spin	singlet
Total Energy	-234.61170280 a.u.
Total Energy	-147,221.09766342 kcal/mol
RMS Gradient Norm	0.00001326 a.u.
Dipole Moment	0.0000 Debye
Point Group	Ci
C-C Bond Length	1.55 and 1.50Å
C=C Bond Length	1.33Å

Since a different basis set was used for the reoptimization it was not possible to compare the total energy of the conformer after the first optimization with the total energy from the second optimization. It was, however, possible to compare the symmetry and the structure of the conformer before and after reoptimization. It is clear that the symmetry of the anti 2 conformer has not changed upon reoptimization as the point group is still C_i, however the structure has changed slightly. The length of the C=C bond has increased by a very small amount, the central C-C bond remained the same length but the other C-C bonds have decreased in length slightly.

Frequency Analysis

This analysis was used to confirm that the structure was a minimum on the potential energy surface. The convergence in the optimization calculations confirm the presence of a stationary point, however to confirm the nature of this point (maximum or minimum) the second derivative of the function is needed. The presence of only real vibrational frequencies would confirm that the structure was a minimum.

The frequency analysis was completed by running the reoptimized (B3LYP 6-31G^*) anti 2 again, using the same method and basis set, but this time the keyword optimize was replaced by frequency. This produced the vibrational modes of the molecule, all of which were positive, and therefore real. This confirmed that the structure calculated was a minimum on the potential energy surface.

The lowest vibrational mode was at 74.26cm^-1

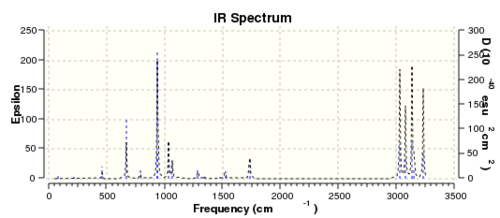
The thermochemical data for the molecule was also found and is displayed below:

Table 5. Thermochemical data for anti 2 after reoptimisation and frequency analysis

	Equation	Value (a.u.)	Value (kcal/mol)
Sum of electronic and zero-point energies	E0K = Eelec + ZPE	-234.469204	-147,131.678297
Sum of electronic and thermal energies	E298K = E0K + Evib + Erot + Etrans	-234.461857	-147,127.067984
Sum of electronic and thermal enthalpies	H = E298K + RT	-234.460913	-147,126.475615
Sum of electronic and thermal free energies	G = H - TS	-234.500778	-147,151.491286

Optimizing the "Chair" and "Boat" Transition Structures

Chair Transition State

Hessian Method

First, two allyl fragments were drawn out in GaussView and optimized using the HF 3-21G method. They were then arranged into position to approximately form the chair transition state, and the two fragments were given a set separation of 2.2Å between the two sets of terminal carbons. This transition state was the optimized to a transition state using the Optimization to a TS (Berny) calculation and the force constants were calculated once. The additional keyword Opt=NoEigen was also added which would stop the calculation from crashing if more than one imaginary frequency was detected.

Hessian optimized chair transition state:

The result of this calculation yielded the expected imaginary vibrational mode at -817.97cm^-1, this corresponds to the motion which leads to the formation of a covalent bond between the two terminal carbons of the allyl fragments. The distance between the terminal carbons in the optimized transition state was 2.02Å for both sets of terminal carbons. The point group of the molecule was found to be C_2h and had total energy= -231.61932221 a.u. confirming that the correct transition state had been modeled, due to the close agreement with the values in appendix 2 of the lab script.

The thermochemical data for the transition state was found and is shown in table below:

Table 6. Thermochemical data for chair TS (Hessian method), HF 3-21G

	Equation	Value (a.u.)	Value (kcal/mol)
Sum of electronic and zero-point energies	E0K = Eelec + ZPE	-231.46669	-145,247.57191
Sum of electronic and thermal energies	E298K = E0K + Evib + Erot + Etrans	-231.461340	-145,244.214738
Sum of electronic and thermal enthalpies	H = E298K + RT	-231.460396	-145,243.622369
Sum of electronic and thermal free energies	G = H - TS	-231.495205	-145,265.465351

Frozen Co-ordinate Method

Another method for modeling the transition state is to first freeze the reaction coordinate, and first optimize the rest of the molecule. Once the molecule is optimized the reaction co-ordinate can be unfrozen, then the whole system is optimized again, this can give more accurate modeling of the transition state if the estimated structure is far from the real structure. This approach can also be quicker than the Hessian method as it differentiates along the reaction coordinate rather than calculating force constants, which can be time consuming.

As with the Hessian method, the first step was to produce two optimized (HF 3-21G) allyl fragments arranged such that they resemble a chair structure, with the fragments seperated by 2.2Å at the terminal carbons. The distance between the fragments is fixed at 2.2Å for the optmization by identifying the terminal carbons of the two fragments as a bond, and selecting to Freeze Coordinate. The optimization of the rest of the molecule was then run (HF 3-21G for a minimum). The reaction coordinate was unfrozen, and the Derivative of the bonds between allyl fragments was calculated by a second optimization (opt+freq), but this time optimized to a TS (berny).

Freeze Coordinate optimized chair transition state:

The result of this calculation agreed well with the Hessian method above. The point group was C_2h and the total energy was -231.61932240 a.u. which matches the values stated above closely. The distance between the terminal carbons was 2.02Å which again agrees with the data calculated using the Hessian method. The imaginary frequency at -817.82cm^-1 was seen again, which correlates the action of forming a bond between the two allyl fragment terminal carbons.

Table 7. Thermochemical data for Frozen Coordination chair transition state

	Equation	Value (a.u.)	Value (kcal/mol)
Sum of electronic and zero-point energies	E0K = Eelec + ZPE	-231.466700	-145,247.578189
Sum of electronic and thermal energies	E298K = E0K + Evib + Erot + Etrans	-231.461340	-145,244.214738
Sum of electronic and thermal enthalpies	H = E298K + RT	-231.444361	-145,243.622369
Sum of electronic and thermal free energies	G = H - TS	-231.479778	-145,265.466606

Boat Transition State (QST2 Method)

This method involves defining the reactants and products, then the calculation interpolates between the initial and final structures in order to find the transition state. This means that the labeling of atoms becomes important, so that the calculation knows where bonds are being made/ broken.

The anti 2 structure (C_i) of 1,5 hexadiene was used as the reactant and product, however the labeling was changed for the product, to show where a bond had been broken, and another had formed. The calculation was set up using the Opt-Freq job type and TS (QST2), again using HF 3-21G. The calculation fails to correctly model the transition state, as shown by the image below, where a chair like transition state forms. The geometries of the reactant and product did not closely match the boat transition state structure, causing the calculation to just move one allyl fragment in a translational fashion, disregarding any possible rotation.

QST2 failed calculation of boat transition state:

The reactant and product structures were then modified so that the dihedral angle around the central C-C-C-C was 0^o and the angles of the terminal C-C-C bonds were set to 100^o. The same calculation method was used again in this case, and it correctly predicted the boat transition state.

QST2 successful calculation of boat transition state:

The total energy of the transition state is -231.60280243 a.u. and the point group is C_2v, confirming the presence of the boat transition state, due to the close agreement with the values given in appendix 2 of the script. The separation between the allyl fragments was 2.14Å. There was one imaginary frequency at -840.14cm^-1, this corresponded to the formation of a bond between the terminal carbons of the allyl fragments.

Table 8. Thermochemical data for QST2 boat transition state

	Equation	Value (a.u.)	Value (kcal/mol)
Sum of electronic and zero-point energies	E0K = Eelec + ZPE	-231.450934	-145,237.684873
Sum of electronic and thermal energies	E298K = E0K + Evib + Erot + Etrans	-231.445305	-145,234.152621
Sum of electronic and thermal enthalpies	H = E298K + RT	-231.444361	-145,233.560252
Sum of electronic and thermal free energies	G = H - TS	-231.479778	-145,255.78476

Intrinsic Reaction Coordinate

Since it is very difficult to identify which conformer of 1,5 hexadiene is related to a given transition state, by simply looking at the geometry, an IRC calculation must take place in order to show which conformer the product will be. An IRC calculation involves taking a series of small steps, where the geometry changes by a small amount, in the direction where the gradient of the potential energy surface is steepest. These calculations can be carried out in both the forward and reverse direction, but because this reaction is symmetric about the transition state only the forward direction was used.

The IRC calculation was carried out on the already optimized transition states, for the chair TS the Frozen Coordinate optimized transition state was used, for the boat TS the QST2 optmized transition state was used. In both cases the force constants were calculated at every step and it was specified that 50 points should be calculated along the IRC, this lead to convergence on a minimum in both cases so no further calculation was necessary.

Intrinsic reaction coordinate and video of bond formation for the chair TS:

For the chair TS the intrinsic reaction coordinate took 44 (of the 50 specified) steps to reach a minimum, it is clear that a minimum was reached as the graph flattens towards the end of the plot. The energy of this minimum point was -231.69157863 a.u. and the structure at the minimum had the point group C₂ which lead to the suggestion that the product formed is the gauche 2 conformer (C₂), due to close agreement of the total energy value and the fact both structures have the same point group.

Intrinsic reaction coordinate and video of bond formation for the boat TS:

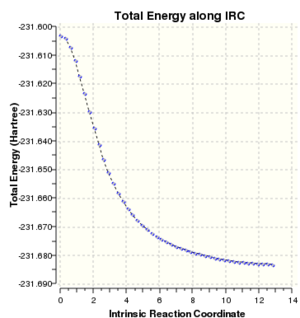
For the boat TS the intrinsic reaction coordinate took 45 of the 50 specified steps, again it is clear that a minimum was reached due to the flattening towards the end of the plot. The energy of the final product via the boat transition state was -231.68298167 a.u. with the point group C_s. This corresponds to the modified reactant that was used for the QST2 calculation (ie. with central C-C-C-C dihedral angle of 0^o), which means that the guess structure was not good enough. Another calculation using QST3 method could be done in future, as this is likely to give a better guess, which would likely result in a correct prediction of the product formed as the lowest energy conformer (Gauche 3).

Activation Energies

The activation energy of the reaction via each transition state can be calculated by finding the difference in energy between the reactant structure (anti 2) and the transition state energy. This was done for both chair and boat transition states, using optimizations at both low level (HF 3-21G) and higher level (B3LYP 6-31G^*) of theory.

Chair Transition State Reoptimization (B3LYP 6-31G^*)

Chair Reopt

The total energy of the reoptimized chair transition state was -234.55698303 a.u., the point group was C_2h and the distance bewteen the terminii of the allyl fragments is 1.97Å, which is smaller than the separation predicted using the lower level of theory (HF 3-21G). Below is the thermochemcial data:

Table 9. Thermochemical data for reoptimized chair transition state

	Equation	Value (a.u.)	Value (kcal/mol)
Sum of electronic and zero-point energies	E0K = Eelec + ZPE	-234.414929	-147,097.620213
Sum of electronic and thermal energies	E298K = E0K + Evib + Erot + Etrans	-234.409009	-147,093.905356
Sum of electronic and thermal enthalpies	H = E298K + RT	-234.408064	-147,093.31236
Sum of electronic and thermal free energies	G = H - TS	-234.443814	-147,115.745828

Boat Transition State Reoptimization (B3LYP 6-31G^*)

Boat Reopt

The total energy of the reoptimized boat transition state was -234.54309290 a.u., the point group was C_2v, and the distance between the terminal carbons of the allyl groups is 2.21Å. This separation is larger than that for the lower level theory optimization (HF 3-21G). The thermochemical data is shown below:

Table 10. Thermochemical data for reoptimized boat transition state

	Equation	Value (a.u.)	Value (kcal/mol)
Sum of electronic and zero-point energies	E0K = Eelec + ZPE	-234.402351	-147,089.727397
Sum of electronic and thermal energies	E298K = E0K + Evib + Erot + Etrans	-234.396014	-147,085.750869
Sum of electronic and thermal enthalpies	H = E298K + RT	-234.395070	-147,085.1585
Sum of electronic and thermal free energies	G = H - TS	-234.431762	-147,108.183083

Summary of Energies and Calculations of Activation Energies

Summary of energies

	HF/3-21G			B3LYP/6-31G*
	Electronic energy (a.u.)	Sum of electronic and zero-point energies (a.u.)	Sum of electronic and thermal energies (a.u.)	Electronic energy (a.u.)	Sum of electronic and zero-point energies (a.u.)	Sum of electronic and thermal energies (a.u.)
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466700	-231.461340	-234.556983	-234.414929	-234.409009
Boat TS	-231.602802	-231.450934	-231.445305	-234.543093	-234.402351	-234.396014
Reactant (anti2)	-231.692535	-231.539538	-231.532568	-234.611703	-234.469204	-234.461857

These values agree very well with the values quoted in appendix 2 of the script, confirming that the calculations for the transition states and reactant were correct. This data alone, however, does not indicate which transition state is preferred; so the activation energy for each reaction was calculated (using the difference in energy between the TS and the reactant).

Summary of activation energies (kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.70	34.05	33.16	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.95	41.32	44.7 ± 2.0

Again these values match those in appendix 2 closely. It can be seen that the activation energies using the higher level of theory (B3LYP 6-31G^*) were a closer match to the experimental values than the activation energies calculated using HF 3-21G. More importantly, it is clear that activation energy of the reaction, via the chair transition state, is much lower than activation energy of the reaction that proceeds via the boat transition state. This data indicates that the reaction is likely to proceed via the chair transition state, since this pathway is more easily attainable.

The Diels Alder Reaction

Introduction

The Diels-Alder reaction is the pericyclic cycloaddition of a conjugated cis-diene and a dieneophile, forming a cyclohexene based product,and is a _π4_s + _π2_s thermal reaction. Since it involves 6π electrons(4n+2) and is a thermal process, the reaction must proceed suprafacially with Hückel topology. The reaction can produce either an exo or endo product, with the selectivity being goverened by the stability of the transition state. The HOMO of one of the reactants interacts with the LUMO of the other reactant in forming the bonds in this reaction, the extent of overlap depends on the symmetry of the molecular orbitals, so both must be symmetric or both must be antisymmetric for the reaction to take place. The aim of this part experiment was to model a simple Diels-Alder reaction (cis-butadiene and ethene) and investigate the reactants and transition states. Also a more complex Diels-Alder (cyclohexa-1,3-diene and maleic anhydride) was modeled in order to investigate the regioselectivity (exo vs. endo) of the reaction.

Diels Alder Reaction of cisbutadiene and ethene

Optimization of Reactants

Cis-butadiene

First, cis-butadiene was drawn out in GaussView, then optimized using the semi-empirical AM1 method, this method was used as higher levels of theory (e.g. HF 3-21G) twist the structure, due to the unfavourable A^1,4 strain experienced in the synperiplanar conformer. It would, therefore, no longer be planar, and it would not be able to take part in the Diels-Alder reaction if this was the case.

The optimized structure had total energy = 0.04879718 a.u. and point group = C_2v, the calculated HOMO and LUMO and their respective data is shown below:

Table 11. HOMO and LUMO of cis-butadiene

	HOMO	LUMO
Visualization
Symmetry	Antisymmetric	Symmetric
Energy (a.u.)	-0.34381	0.01707

Ethene

Ethene was drawn out in GaussView, and again optimized using the semi-empirical AM1 method. The optimized structure had total energy = 0.02619028 a.u. and the point group = D_2h, the HOMO and LUMO are shown below:

Table 12. HOMO and LUMO of ethene

	HOMO	LUMO
Visualization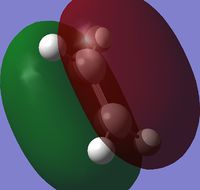
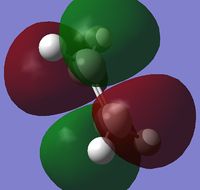Symmetry	Symmetric	Antisymmetric
Energy (a.u.)	-0.38775	0.05283

The HOMO of cis-butadiene and the LUMO of ethene are both antisymmetric, therefore there is a good overlap between these MOs, the same is true for the LUMO of cis-butadiene and HOMO of ethene, except both are symmetric in this case. This means that both HOMO-LUMO interactions are allowed, hence the reaction is allowed.

Optimization and Analysis of the Transition State

The transition state structure was produced by modifying a bicyclo[2,2,2]octane molecule, removing a -CH₂-CH₂- fragment, and breaking the bonds between the ethene and the butadiene fragments. The fragments were then seperated by 2.2Å and the transition state was optimized using the Frozen Coordinate method. The intermolecular distance was frozen to 2.2Å and then the rest of the structure was optmizied to a minimum using the semi-empirical AM1 method. The distance between the reactants was then unfrozen and an opt+freq calculation was carried out on the structure, optimizing to a transition state (Berny) again using the semi-empirical AM1 method.

An image of the transition state is shown below:

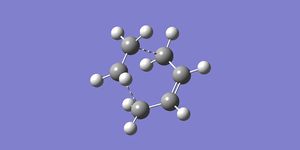
The total energy = 0.11165482 a.u. and the point group = C₁. A frequency analysis was also performed on the transition state, this yielded one imaginary frequency at -955.86 cm^-1 which corresponds to the formation of the new carbon-carbon bonds. From the video below it is clear that this bond formation is concerted, as would be expected for a pericyclic reaction. The lowest positive frequency at 147.17cm^-1 corresponds to a wagging, the motion closely resembles asynchronous bond formation. The imaginary frequency corresponds to a vibration in which the symmetry of the transition state is preserved, however the lowest real symmetry vibrational mode breaks the symmetry.

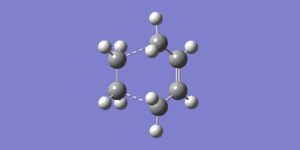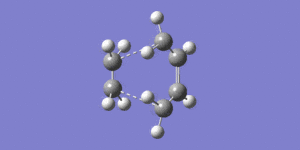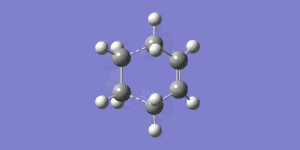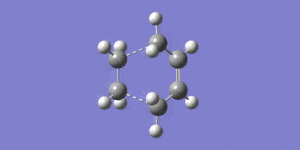
The distance between the ethene and cis-butadiene molecules is 2.12Å, this distance is too large for a bond, but also smaller than twice the size of the van der Waals radius for carbon, confirming that a bond is being made. It is also clear that the reaction is in progress by looking at the carbon-carbon bond lengths in the transition state. The typical sp³-sp³ carbon-carbon bond is 1.54Å, and the sp²-sp² carbon-carbon bond length is 1.34Å. Bond (a) is 1.40Å showing that a double bond is starting to form, as the bond length has shortened from the initial 1.54Å which is expected for an sp³ C-C bond. The bonds that had previously been C=C sp², (b) and (d) have lengthened from 1.34Å to 1.38Å, showing that these bonds are losing double bond character, and hence are tending towards becoming single bonds.

Table 13. HOMO and LUMO of transition state

	HOMO	LUMO
Visualization
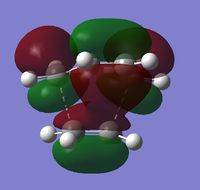Symmetry	Antisymmetric	Symmetric
Energy (a.u.)	-0.32390	0.02313

From the shape and antisymmetric nature of the HOMO of the transition state it is clear that the interaction leading to the transition state's HOMO must be due to the overlap of the HOMO of cis-butadiene and the LUMO of ethene, this is the C-C σ bond. The LUMO of the transition state is symmetric and by the shape it is clear that the LUMO is formed from the interaction between the LUMO of cis-butadiene and the HOMO of ethene, this is the C-C σ^* orbital.

A Study of Regiochemistry - Diels Alder Reaction of cyclohexa-1,3-diene and maleic anhydride

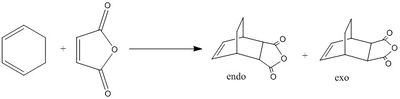
The Diels-Alder reaction between maleic anhydride and cyclohexa-1,3-diene can produce two different products, the exo and the endo adducts. In this case the endo is preferred to the exo isomer with a ratio of 99:1, despite the exo product being the more thermodynamically stable. The reactants were modeled in order to investigate the HOMO-LUMO interactions leading to the transition state, thereby explaining why this interaction is symmetry allowed. The transition states were modeled in order to explain the preference of the endo product.

Optimization of Reactants

Maleic anhydride

Maleic anhydride was drawn out in GaussView and optimized to a minimum using the semi-empirical AM1 method. The total energy of the optimized structure = -0.12182418 a.u. and the point group = C_2v. The HOMO and LUMO are shown below:

Table 14. HOMO and LUMO of maleic anhydride

	HOMO	LUMO
Visualization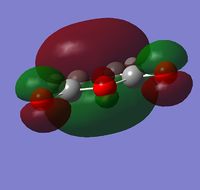
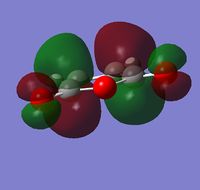Symmetry	Symmetric	Antisymmetric
Energy (a.u.)	-0.44187	-0.05949

Cyclohexa-1,3-diene

The structure of cyclohexa-1,3-diene was drawn out in GaussView and optimized to a minimum using the semi-empirical AM1 method. The total energy = 0.02795807 a.u. and the point group = C_2v. The HOMO and LUMO and their respective data are shown below:

Table 15. HOMO and LUMO of cyclohexa-1,3-diene

	HOMO	LUMO
Visualization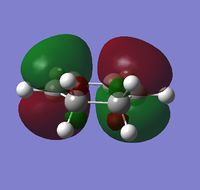
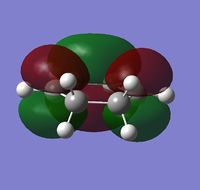Symmetry	Antisymmetric	Symmetric
Energy (a.u.)	-0.32078	0.01698

Optimization and Analysis of the Transition States

Endo Transition State

The endo transition state was modeled by positioning the two reactants in an orientation such that it had a reasonable resemblance to the endo transition state. The two reactant molecule were placed 2.2Å and, again, the transition state was optimized using the frozen coordinate method. The intermolecular distance was frozen and the rest of the structure was optimized as a minimum, the coordinates were then unfrozen and the entire structure was optimized (opt+freq) as a transition state (Berny) using the semi-empirical AM1 method.

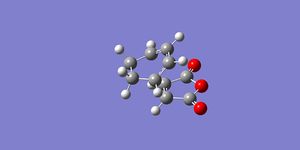
The total energy = -0.05150466 a.u. and the point group = C_s, for the endo transition state. The distance between the two molecules in the transition state is 2.16Å, showing that an interaction is taking place, and the bond is starting to form as the distance is less than two times the van der Waals radius of carbon. A frequency analysis was also performed on the transition state, and the calculation produced one imaginary frequency at -806.42cm^-1 which corresponds to the concerted bond formation, as shown by the video below.

An IRC calculation was carried out on the endo transition state modeled in both the forward and reverse directions, taking 50 points in each direction and using the semi-empirical AM1 method. This was done to verify that the expected product was formed and to calculate an activation energy for the reaction via the endo transition state. The plot of the intrinsic reaction coordinate is shown below along with the final step of the IRC calculation which shows the structure of the product. This is indeed the endo product, confirming that the correct transition state had been formed.

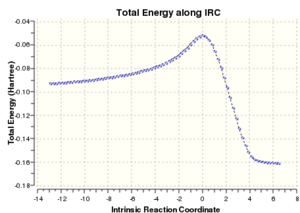
The left hand side of the intrinsic reaction coordinate plot is of the reactants, and the right hand side is the products, and an activation energy for the reaction can be calculated. For this reaction the activation energy was calculated to be 25.61 kcal/mol. The HOMO and LUMO were also produced during the opt+freq calculation and are shown in the table below:

Table 16. HOMO and LUMO of the endo transition state

	HOMO	LUMO
Visualization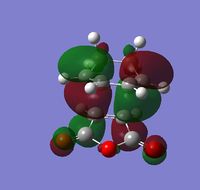
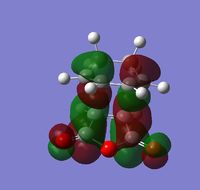Symmetry	Antisymmetric	Antisymmetric
Energy (a.u.)	-0.34497	-0.03572

The fact that both the HOMO and LUMO are antisymmetric suggests that the overlap is due to the HOMO of cyclohexa-1,3-diene and the LUMO of maleic anhydride. This is also clear from the shape of the molecular orbitals which are very similar to those of the MOs of the reactants mentioned above. In the endo transition state there is a stabilizing secondary orbital effect, the C=O π^* orbitals of maleic anhydride can interact with the C=C π orbital of the diene. This can be seen in the HOMO as the electron density on the carbonyl oxygen atoms is of the correct phase to interact with the diene and is in reasonable proximity of it (on the same side of the structure).

The bond lengths of the endo transition state are shown below, and are used for later comparison with the exo transition state structure:

The C-C bonds which form the bridge are found to be close to the expected sp³ C-C value (1.54Å), the C-C bonds of the 'cis-diene' part of cyclohexadiene and the alkene C-C of maleic anhydride all have bond lengths in the region between single(sp³) and double C-C (sp²) bond values. This shows that the reaction is in progress, and the bonds that were formerly C=C bonds in the reactants are tending towards C-C (single bond) character and the C-C bond of the cis-diene part is becoming closer to C=C (double bond) character, as is expected in the product. The separation of the -(C=O)-O-(C=O)- part of maleic anhydride with the -HC=CH- of the cyclohexa-1,3-diene was 2.89Å.

Exo Transition State

The exo transition state was modeled in the same way, except this time the maleic anhydride was rotated 180^o to reflect the different approach in the exo transition state. The two reactant molecule were placed 2.2Å and, again, the transition state was optimized using the frozen coordinate method. The intermolecular distance was frozen and the rest of the structure was optimized as a minimum, the coordinates were then unfrozen and the entire structure was optimized (opt+freq) as a transition state (Berny) using the semi-empirical AM1 method.

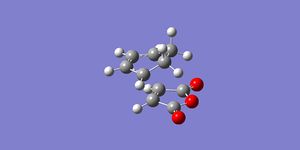
The total energy = -0.05041983 a.u. for the exo transition state. The distance between the two molecules in the transition state is 2.17Å, showing, again, that an interaction is taking place, and that the bond is starting to form. The frequency analysis produced one imaginary frequency at -812.27cm^-1 which again corresponds to the synchronous bond formation, as shown by the video below.

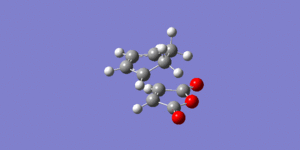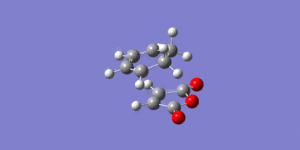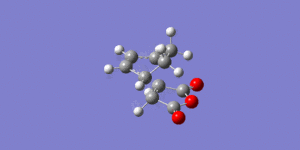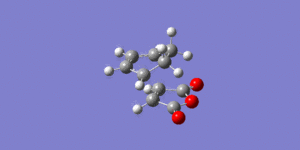
An IRC calculation was carried out for the exo transition state in both the forward and reverse directions, taking 50 points in each direction, calculating the force constants at every point and using the semi-empirical AM1 method. This was done to verify that the expected product was formed and to calculate an activation energy for the reaction via the exo transition state. The plot of the intrinsic reaction coordinate is shown below along with the final structure of the IRC calculation which shows the structure of the product. This is indeed the exo product, confirming that the correct transition state had been formed.

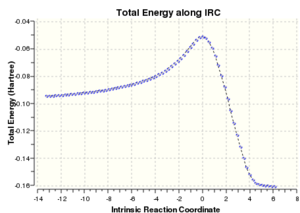
The left hand side of the intrinsic reaction coordinate plot is of the reactants, and the right hand side is the products, and an activation energy for the reaction can be calculated. For this reaction the activation energy was calculated to be 27.39 kcal/mol. The HOMO and LUMO were also produced during the opt+freq calculation and are shown in the table below:

Table 17. HOMO and LUMO of the exo transition state

	HOMO	LUMO
Visualization
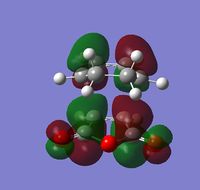Symmetry	Antisymmetric	Antisymmetric
Energy (a.u.)	-0.34285	-0.04039

Again the fact that both the HOMO and LUMO are antisymmetric suggests that the overlap is due to the HOMO of cyclohexa-1,3-diene and the LUMO of maleic anhydride. The shape of the orbitals also closely matches the HOMO of cyclohexadiene and the LUMO of maleic anhydride, further confirming that these orbitals are responsible for the interaction. In the exo transition state it is clear that no stabilizing secondary orbital interaction can take place. In the HOMO the electron density of the diene lies too far (opposite side of the structure) from the electron density of the carbonyls and thus there is no chance for an overlap.

The bond lengths of the exo transition state are shown below:

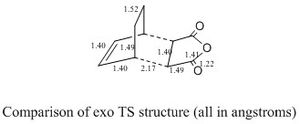
The C-C bonds which form the bridge are found to be close to the expected sp³ C-C value (1.54Å), the C-C bonds of the 'cis-diene' part of cyclohexadiene and the alkene C-C of maleic anhydride all have bond lengths in the region between single(sp³) and double C-C (sp²) bond values. This shows that the reaction is in progress, and the bonds that were formerly C=C bonds in the reactants are tending towards C-C (single bond) character and the C-C bond of the cis-diene part is becoming closer to C=C (double bond) character, as is expected in the product. The distance between the -(C=O)-O-(C=O)- fragment of maleic anhydride and the -CH₂-CH₂- from the cyclohexa-1,3-diene is 2.94Å. The structure is actually very similar to the endo transition state, the only major difference is the separation of the -(C=O)-O-(C=O)- fragment of maleic anhydride with the -CH₂-CH₂- (exo) or -HC=CH- (endo). The exo transition state is likely to be more strained as it's in close proximity to the more bulky group -CH₂-CH₂- (compared to -HC=CH- in endo).

Comparison of Transition States

Despite the exo adduct being lower energy, and therefore the thermodynamic product, the endo transition state is lower in energy than the exo TS, and thus the most stable transition state. This is reflected in the fact that the activation energy of the reaction via the endo transition state is lower than that via the exo TS, thus the endo isomer is the kinetic product. From this it is likely that the reaction is under kinetic control.

The principal reason for the endo transition state being more stable is due to the secondary orbital effect. In the endo transition state there are two additional interactions of the C=O π^* orbitals of the maleic anhydride with the C=C π orbitals of the diene, which are not present in the exo transition state as the C=O π^* orbitals are facing outwards, away from the diene. This secondary orbital interaction has a stabilizing effect on the endo transition state causing it to be lower in energy; and hence highly favoured when the reaction is under kinetic control. The slightly more strained nature of the exo transition state is another contributing factor to the preference of the reaction to proceed via the endo transition state.

Conclusion

Both Diels-Alder reactions have been correctly modeled and the calculations have been able to explain why the reaction is allowed, and also explained the preference of one product over another due to the orbital interactions involved. It has also confirmed that the Diels-Alder is a pericyclic reaction due to the concerted bond formation that takes place. There are, however, some limitations to this experiment. The calculations were done using non-standard conditions compared to actual laboratory conditions, for example the effect of solvents was not considered in the calculations, also temperature and pressure were neglected for these reactions. Therefore, were there more time, or in future, it would be interesting to investigate how these conditions affect the outcome of the calculations. Another element that could be further investigated would be to use different levels of theory in the transition state calculations in order to see whether it had any effect on the calculations.