Rep:Mod:ASP0216

Introduction to Molecular Modelling 2

NH₃ (Ammonia)

Optimisation

Download optimised .log file here

Optimised Ammonia molecule

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP): -56.55776873(au)

RMS Gradient: 0.00000485

Point Group: C_3V

The optimisation used determined the N-H bond length to be 1.01798Å, with a H-N-H bond angle of 105.741º.

 Item                     Value        Threshold   Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES 

Vibrations:

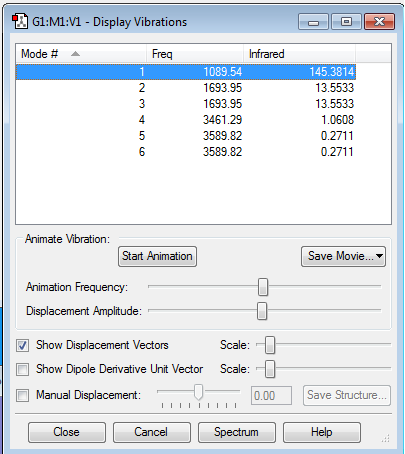
Optimisation of the ammonia structure found six vibrational modes. This is expected from the 3N-6 rule in which, for non-linear systems, the number of vibrational modes = 3N-6, for N is the number of atoms present in the molecule (for ammonia N=4). Some of these vibrational modes are degenerate (have the same energies), such as the two modes calculated to be at 1694 cm^-1 and 3590 cm^-1. Modes #1, 2 and 3 are caused by bending of the N-H bonds and modes #4, 5 and 6 are due to stretching of the N-H bonds. The symmetric stretching of the N-H bonds is observed in mode #4, at 3461 cm^-1. Mode #1 is the umbrella mode, which is a symmetric bend, that when animated looks like an umbrella opening and closing. In an infrared spectrum of ammonia only 2 vibrational modes #1, at 1090 cm^-1, and #2, at 13 cm^-1, are visible as these are the only vibrational mode with a change in dipole moment. No change in dipole moment occurs for the symmetrical stretches, hence these modes are IR inactive.

The values of charge on the nitrogen and hydrogens in ammonia were calculated to be:

Charge on N: -1.125

Charge on H: 0.375

Nitrogen is more electronegative than hydrogen, hence electrons in N-H bonds are pulled closer to the nitrogen atom, giving the nitrogen atom a slight negative charge and hydrogen a slight positive charge.

H₂ optimisation

Download optimised H₂ .log file here

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP): -1.17853935(au)

RMS Gradient: 0.00003809

Point Group: D_{$\mathrm{\infty }h$}

H-H bond length: 0.74289 and bond angle: 180°

 Item                     Value        Threshold   Converged?
 Maximum Force            0.000066     0.000450     YES
 RMS     Force            0.000066     0.000300     YES
 Maximum Displacement     0.000087     0.001800     YES
 RMS     Displacement     0.000123     0.001200     YES 

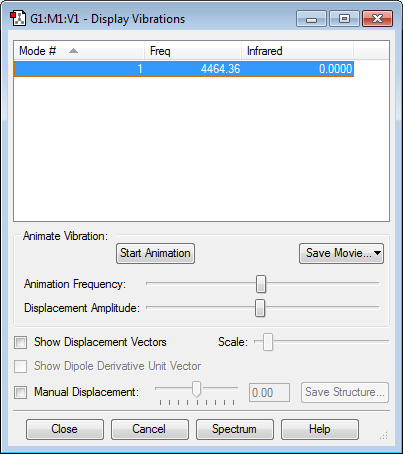
Vibrations:

N₂ optimisation

Download optimised N₂ .log file here

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP): -109.52412867(au)

RMS Gradient: 0.00008380

Point Group: D_{$\mathrm{\infty }h$}

Bond length: 1.10555Å and bond angle: 180°

 Item                     Value        Threshold   Converged?
 Maximum Force            0.000145     0.000450     YES
 RMS     Force            0.000145     0.000300     YES
 Maximum Displacement     0.000045     0.001800     YES
 RMS     Displacement     0.000064     0.001200     YES 

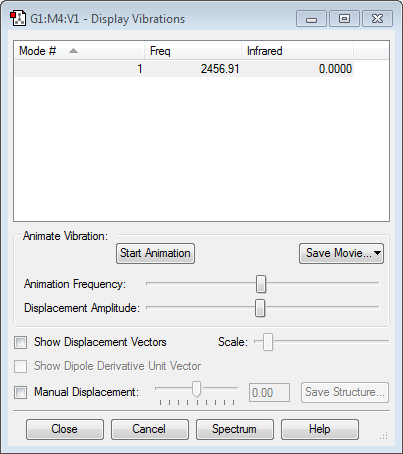
Vibrations:

Haber-Bosch Process

N₂ + 3H₂ -> 2NH₃

E(NH3)= -56.55776873 au

2*E(NH3)= -113.11553746 au

E(N2)= -109.52412867 au

E(H2)= -1.17853935 au

3*E(H2)= -3.53561805 au

ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -113.11553746 – (-109.52412867+-3.53561805) = -0.05579074 au = -146.478599028 kJ/mol = -146.48 kJ/mol (2 d.p.)

As ΔE for the reaction is negative, the products are more stable than the reactants in the Haber-Bosch process. The value obtained using the optimised values is more negative than literature values (-45.9kJ/mol)

Project molecule

BH₄^-

Download optimised .log file here

Optimised Borohydride Anion

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP): -27.24992701(au)

RMS Gradient: 0.00000671

Point Group: T_D

B-H bond length: 1.23933Å and H-B-H bond angle: 109.47°

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000013     0.000450     YES
 RMS     Force            0.000007     0.000300     YES
 Maximum Displacement     0.000065     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES 

The values of charge on the boron and hydrogen atoms were calculated to be:

Charge on B: -0.615

Charge on H: -0.096

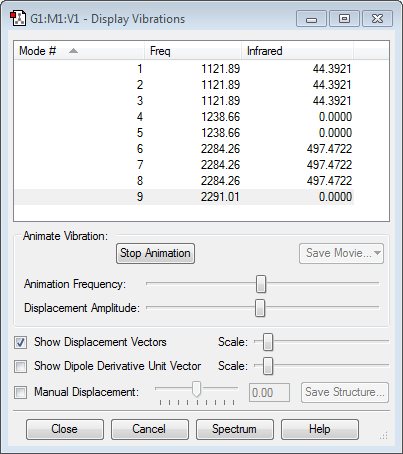
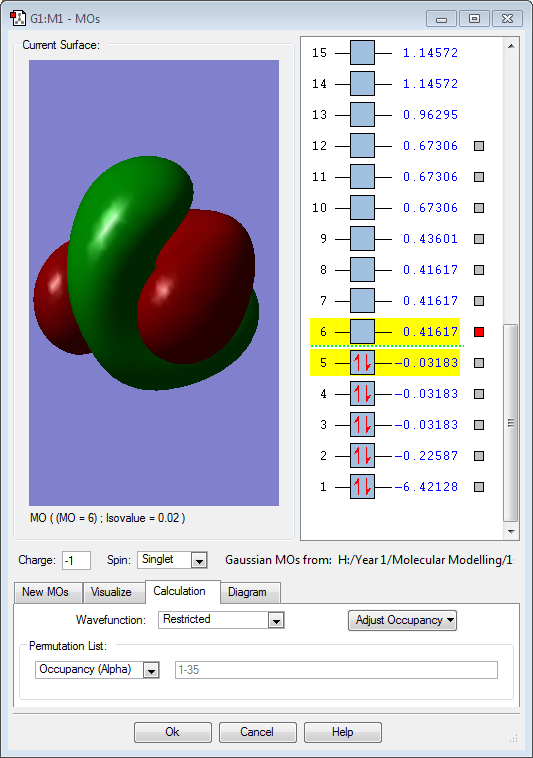
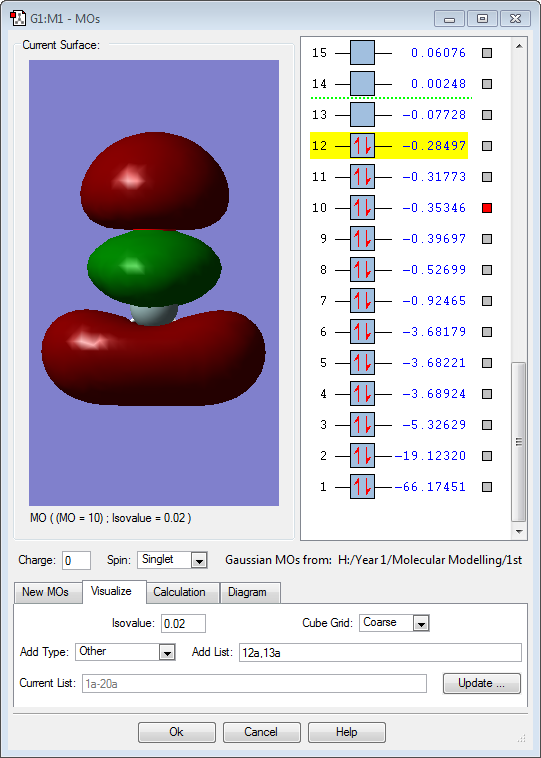
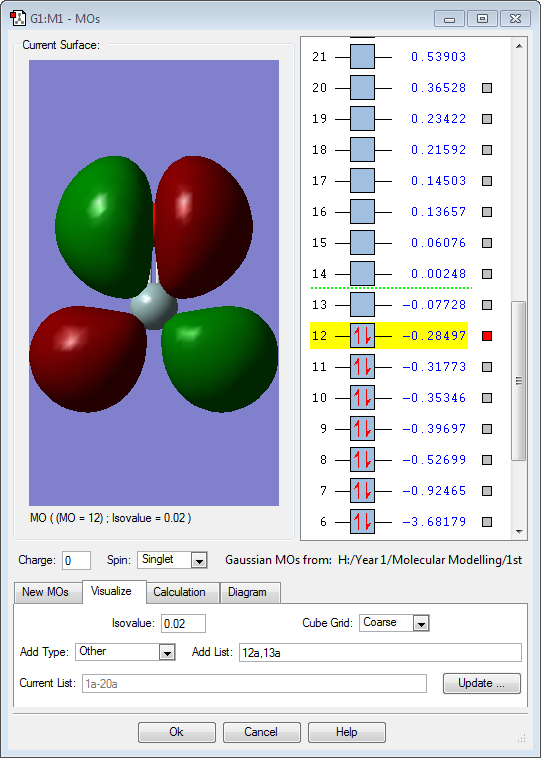
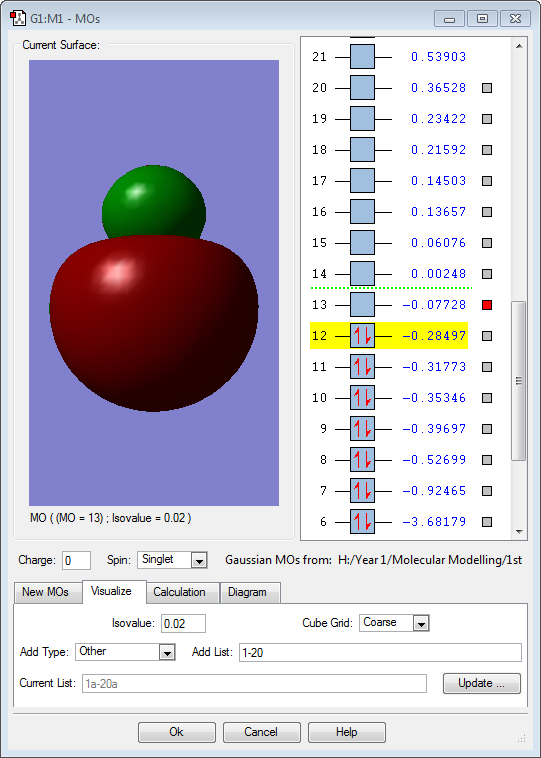
Hydrogen is slightly more electronegative than the boron atom, so electron density should be drawn towards the hydrogen atoms. However, the results above show the opposite. The molecular orbitals below show that a large proportion of electron density is centered around the boron atom and not the hydrogen. Vibrations:

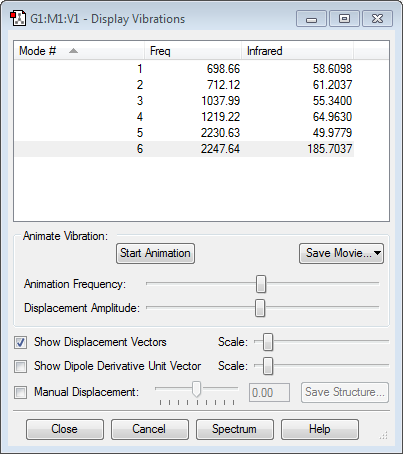
According to the 3N-6 rule (N=5), boron has 9 vibrational modes, as shown above. The first 3 modes are B-H bending vibrations and are degenerate, as are modes #6,7 and 8 which are B-H stretches. In a boron IR spectrum, only 2 peaks are present of the vibrational modes shown above. The peaks have the frequencies 1122 cm^-1 (due to B-H bending) and 2284 cm^-1 (due to stretching of the B-H bonds). Modes #3 and #4 are symmetrical bends and mode #9 is a symmetrical stretch, which produce no change in dipole moment and, hence, are IR inactive

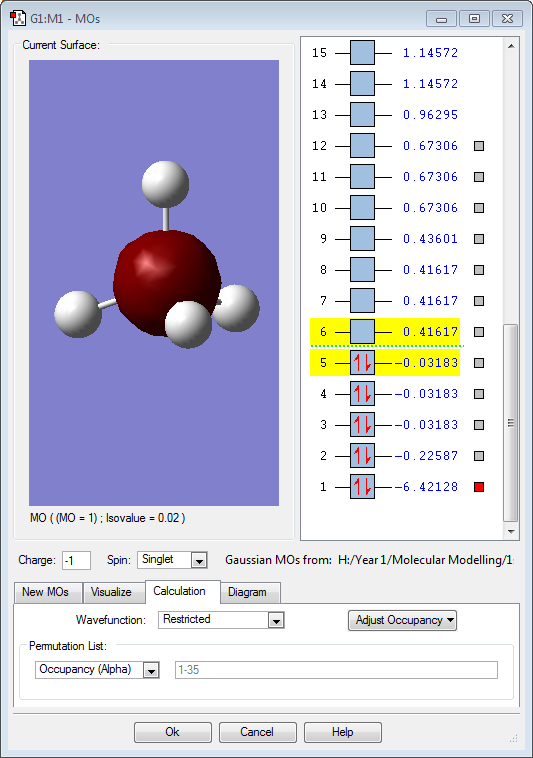
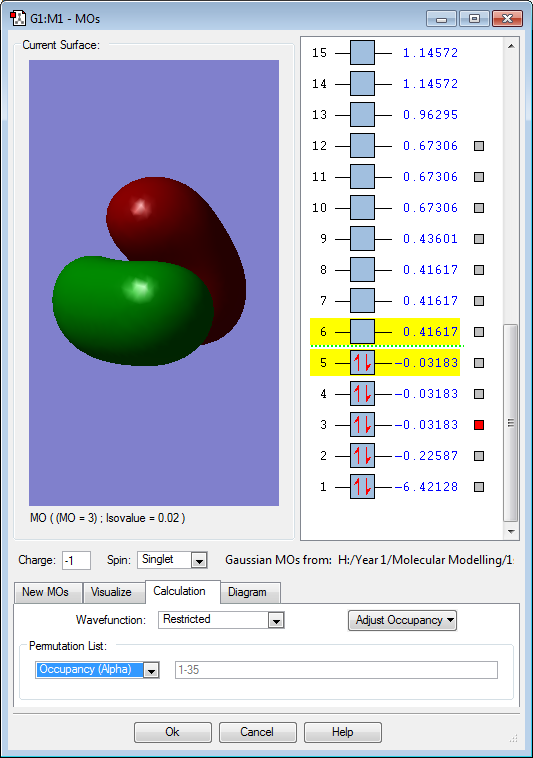
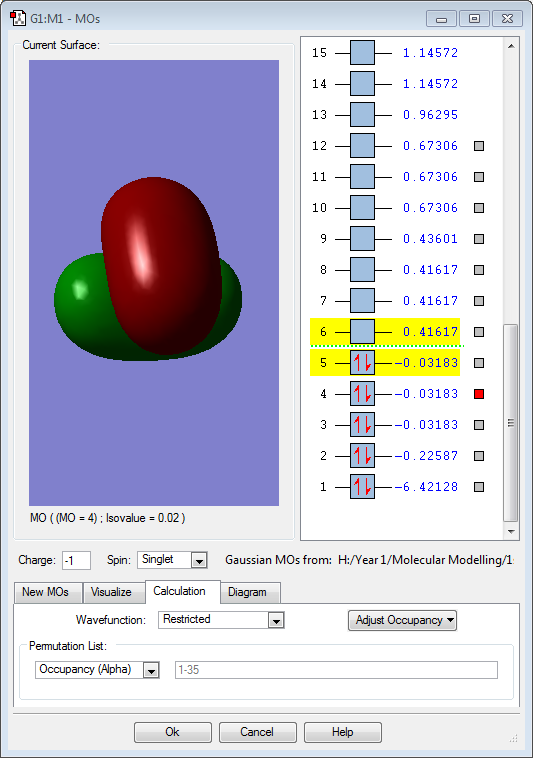
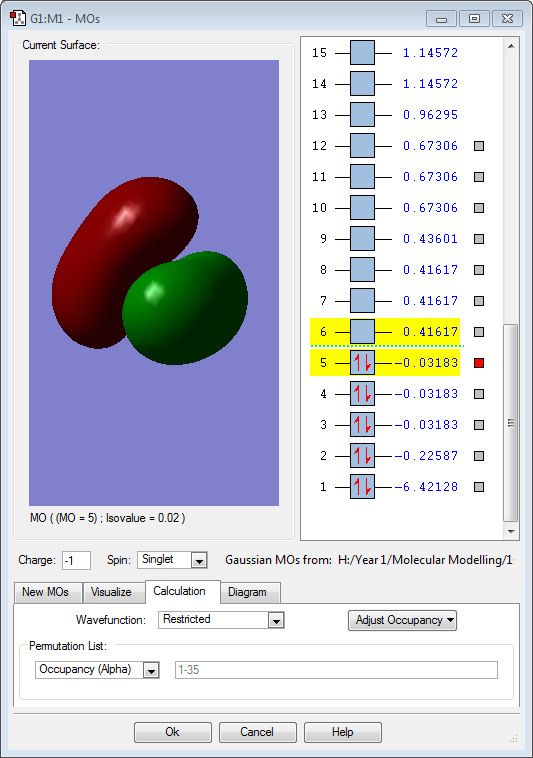
Molecular Orbitals

The 4 hydrogen 1s atomic orbitals combine in a tetrahedral (cubic) arrangement in phase or out of phase. These combine with the valence boron atomic orbitals, 2s and 2p, to produce molecular orbitals.

The above image (MO1) is of the lowest energy orbital for borohydride. It is a non-bonding σ orbital and is combined from a boron 1s atomic orbital.

The 3 above images (MO3/4/5) are of the HOMO for borohydride and are degenerate. They are formed by an in-phase combination of the boron 2p atomic orbitals and the 3 hydrogen ligand group orbitals (which are out of phase). Each of these molecular orbitals is fully occupied.

The above image (MO6) is of the LUMO for borohydride, which is an antibonding orbital. It is formed by an out-of-phase combination of the boron 2s atomic orbital and the in phase hydrogen ligand group orbital. This orbital is unoccupied in borohydride.

H₂SiO

Download optimised .log file here

Optimised Silanone molecule

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP): -365.90001403(au)

RMS Gradient: 0.00001092

Point Group: C_2v

Si=O bond length: 1.53173Å

Si-H bond length: 1.48652Å

H-Si=O bond angle: 124.15711°

H-Si-H bond angle: 111.68587°

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000028     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000056     0.001800     YES
 RMS     Displacement     0.000032     0.001200     YES 

Vibrations:

According to the 3N-6 rule (N=4), silanone has 6 vibrational modes, as shown above. In a silanone IR spectrum, all vibrational modes are present as peaks, as all the modes are asymmetric. The first 3 peaks are bending and the last 3 are stretching.

The values of charge on the silicon, oxygen and hydrogen atoms were calculated to be:

Charge on Si: 1.472

Charge on O: -1.001

Charge on H: -0.236

Is is expected as oxygen is the more electronegative atom in the molecule, so electron density is drawn away from the silicon atom towards the oxygen. Also, hydrogen is more electronegative than silicon, so electron density is drawn towards the hydrogen atoms, but there is a smaller negative charge on the hydrogen atoms compared to the oxygen, as hydrogen is less electronegative than oxygen.

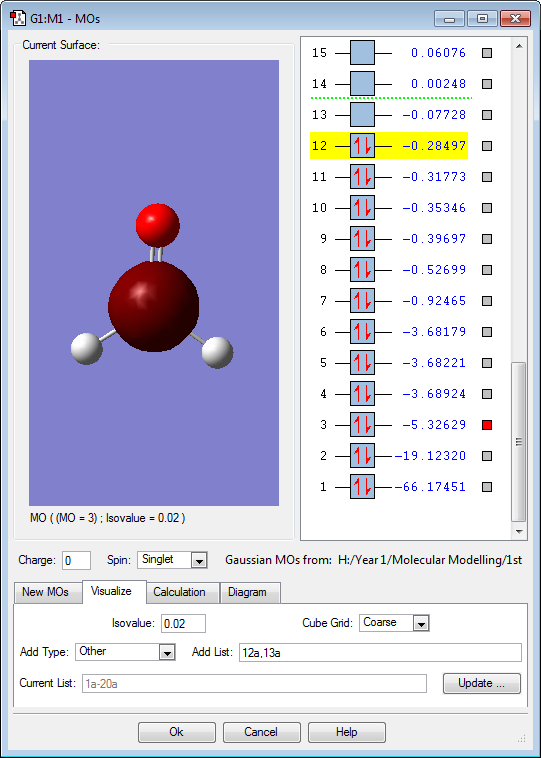
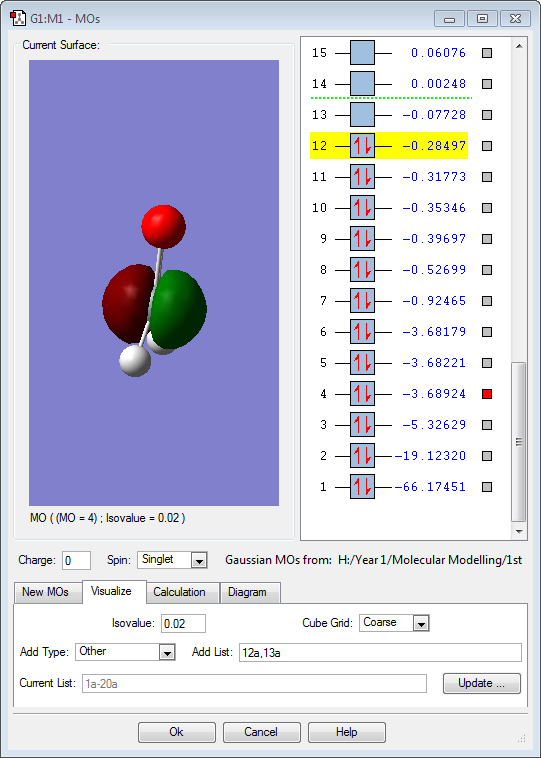
Molecular Orbitals

The above molecular orbital is the HOMO

The above molecular orbital is the LUMO. There is a small energy difference between the HOMO and LUMO, making them very reactive. This is due to unfavourbale overlap between silicon and oxygen p orbitals, creating a weak π bond.