Rep:Mod:ASD321
NH3
Optimized N-H bond distance = 1.01798 Angstrom
Optimized H-N-H bond angle = 105.74115 degrees
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Calculation type: OPTF (optimize and frequency analysis)
Symmetry:C3v
Final Energy(RB3LYP): -56.5577683 a.u.
RMS gradient: 0.00000485 a.u.
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986276D-10
Optimization completed.
-- Stationary point found.
Ammonia |
The optimisation file is linked to here
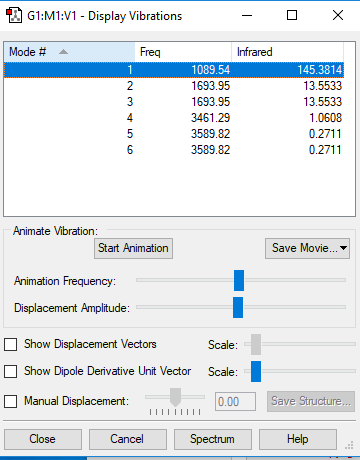
You would expect 6 vibration modes from this molecule.
Modes 2/3 and 5/6 are degenerate.
Modes 1,2 and 3 are bending modes and modes 4,5 and 6 are vibrational modes.
Mode 4 is highly symmetric. Mode 1 is the umbrella mode.
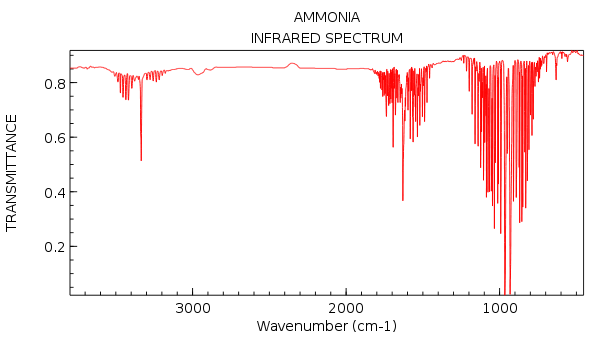
There's 3 bands in the infrared spectrum. This is produced by the first mode (bending), second mode (bending) and fourth mode (stretching). However from the computational results we would only expect to see two peaks as in most infrared spectrum's as the intensity of peaks 4,5 and 6 are so low that they would usually be lost to noise so only peaks 1 and 2/3 (which are degenerate so would appear as 1 peak) would be visible.
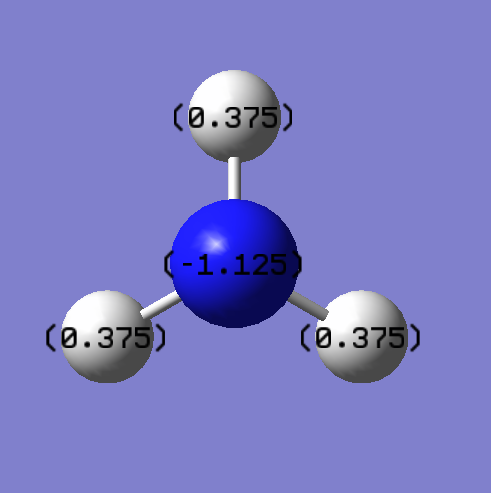
It would be expected that the nitrogen atom would have a negative charge and the hydrogen atoms would be positively charged as nitrogen it more electronegative than hydrogen therefore would pull electron density away from the hydrogen atoms causing the nitrogen to be negatively charged and the hydrogen positively charged. The actual charges are: -1.125 for nitrogen and +0.375 for hydrogen.
The Haber-Bosch Process
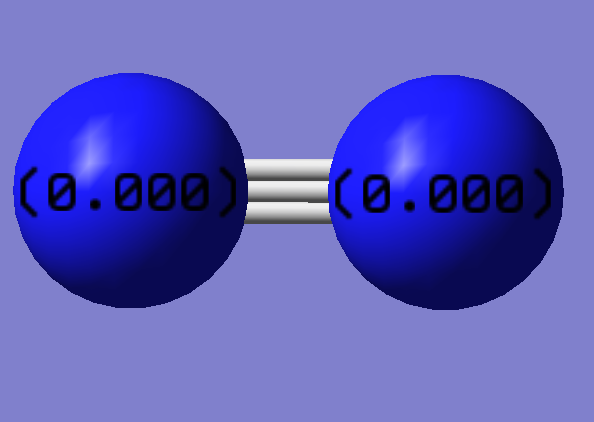
Nitrogen
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Symmetry:D∞h
Calculation type: OPTF (optimize and frequency analysis)
Final Energy (RB3LYP): -109.52412868 a.u.
RMS Gradient: 0.00000060
Bond angle = 180 degrees
Optimized Bond Length: 1.10550 Angstroms
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401025D-13
Optimization completed.
-- Stationary point found.
Nitrogen |
The optimisation file is linked to here
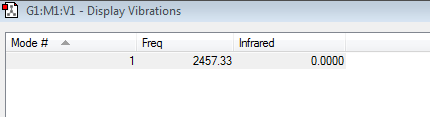
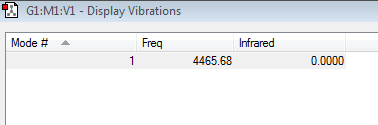
You would expect 1 vibrational mode from the formula: Vibrational modes=3N-5 , for linear molecules. So there can only be 1 band in the infrared spectrum. There is also 0 infrared intensity for this stretch as a stretch of the bond would lead to no overall change in dipole moment.
It would be expected that there would be no overall charge on either nitrogen atom as both have equal electronegativity so shared electrons feel an equal attraction to both nuclei.
Hydrogen
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Symmetry:D∞h
Calculation type: OPTF (optimize and frequency analysis)
Final Energy (RB3LYP):-1.17853936 a.u.
RMS Gradient: 0.00000017 a.u.
Bond Angle= 180 degrees
Optimized Bond Length: 0.74279 Angstroms.
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
Hydrogen |
The optimisation file is linked to here
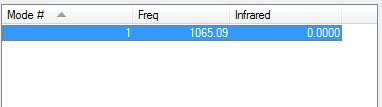
You would expect 1 vibrational mode from the formula: Vibrational modes=3N-5 , for linear molecules. So there can only be 1 band in the infrared spectrum. There is also 0 infrared intensity for this stretch as a stretch of the bond would lead to no overall change in dipole moment.
It would be expected that there would be no overall charge on either hydrogen atom as both have equal electronegativity so shared electrons feel an equal attraction to both nuclei.
The Haber-Bosch Process Energies
E(NH3)=-56.5577683 a.u. = -148,492.42 KJ/mol
2*(NH3)= -113.1155366 a.u. = -296,984.84 KJ/mol
E(N2)= -109.52412868 a.u. = -287,555.60 KJ/mol
E(H2)= -1.17853936 a.u. = -3,094.26 KJ/mol
3*E(H2)= -3.53561808 a.u. = -9,282.77 KJ/mol
ΔE=(2*E(NH3))-((3*E(H2))+(E(N2))=-0.05578984 a.u. = -146.48 KJ/mol
The ammonia product is more stable at room temperature as energy is released in the formation of this product indicating ammonia is of a lower energy than the gaseous reactants therefore more stable.
This is a greater release of energy than the experimental values of -92.4 KJ/mol [2]. This is as we calculated the enthalpy change at lower pressure expecting all the reactants to form products whereas the Haber-Bosch process is in equilibrium and is carried out at higher temperatures and pressures. This results in some of the formed ammonia reverting back to the reactants causing the overall enthalpy change to be lower than the theoretically predicted value.
Fluorine
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Calculation type: OPTF (optimize and frequency analysis)
Point Group: D∞h
Final Energy (RB3LYP): -199.49825218 a.u.
RMS Gradient: 0.00007365
Bond Angle= 180 degrees
Optimized Bond Length: 1.40281 Angstroms
Item Value Threshold Converged?
Maximum Force 0.000128 0.000450 YES
RMS Force 0.000128 0.000300 YES
Maximum Displacement 0.000156 0.001800 YES
RMS Displacement 0.000221 0.001200 YES
Predicted change in Energy=-1.995024D-08
Optimization completed.
-- Stationary point found.
Fluorine |
The optimisation file is linked to here
You would expect 1 vibrational mode as fluorine is a linear diatomic molecule. There is also 0 infrared intensity for this stretch as a stretch of the bond would lead to no overall change in dipole moment therefore is infrared inactive.
Fluorine has no net charge on either atom either as they both have the same electronegativity so shared electrons experience the same effective nuclear charge from each nucleus.
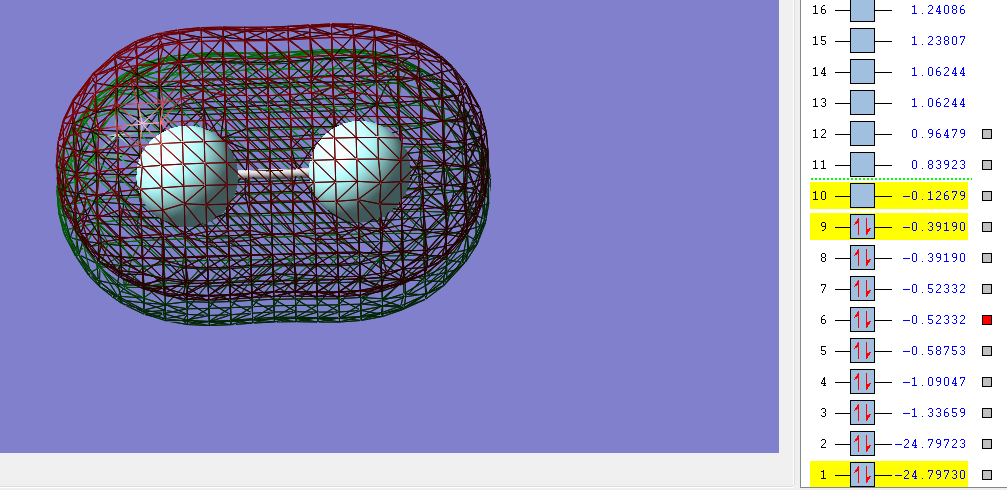
The sigma bonding orbital is filled with two electrons from two 2p orbitals,one from each fluorine, this sigma bond creates a single bond between the two fluorine atoms.
The Pi bonding orbital is filled with two electrons from two 2p orbitals and should lead to the formation of a Pi bond.
However the fluorine Pi anti-bonding orbital is also filled with two electrons from two 2p orbitals which prevents the formation of the Pi bond.
The second sigma molecular orbital filled is from two electrons from 2s orbitals, one from each fluorine atom which should create a single bond between the atoms.
But as there's sufficient electrons available from the two 2s orbitals from each fluorine atom to also fill the second sigma* (antibonding) orbital this bond does not form. In the sigma* (antibonding) orbital it is also clear where the nodal place is where there is no electron density.
The combination of 2s and 1s orbitals from each fluorine atom does not contribute to the overall bonding of the molecule as bond the bonding and anti-bonding orbitals are both filled leading to no net contribution to the overall bonding. As only the sigma (bonding) orbital filled by 2p electrons and is not cancelled by any electrons in the sigma* anti-bonding orbital (orbital 10 in the images above) the overall bond order is 1. There's also very little mixing of 2s-2p orbitals in diatomic fluorine as the fluorine atom is so electronegative the 2s-2p gap is so large that any mixing is not significant.
References
- ↑ http://webbook.nist.gov/cgi/cbook.cgi?Spec=C7664417&Index=1&Type=IR Accessed on 03/03/2017
- ↑ http://www.ausetute.com.au/haberpro.html Accessed on 02/03/2017.