Rep:Mod:AR2014

Physical Computational Module

The objective of this module is to use a variety of computational techniques to examine the reactivity and transition states of a number of chemical processes. These include modelling the chair and boat conformations of a transition state for the Cope rearrangement and investigating the Diels-Alder reaction by MO analysis.

Cope Rearrangement

The cope rearrangement is a [3,3] sigmatropic rearrangement. It's a pericylic reaction so shows concerted movement of electrons. This rearrangement has been extensively studied with 1,5 dienes such as the one modelled here. In this experiment, both transition states, the chair and the boat, will be investigated using a range of different methods.

Optimising Reactants and Products

The Hartree Fock method with a 3-21G basis set was used to investigate the energies of a range of conformers of 1,5-hexadiene.

Energies and Point Groups of various conformations of 1,5-hexadiene

Conformation	Dihedral Angle	Point Group	Total Energy (Hartrees)
Antiperiplanar	180	C2h	-231.69260
Gauche	60	C2	-231.68916
Synperiplanar	120	C2	-231.69167

The Gauche conformation above most closely resembled that of Gauche 6 in the given table. They have the same energy of -231.68916 Hartrees. and the same point group of C1.

Gauche 6

The lowest energy conformer would be expected to be antiperiplanar rather than gauche. This is due to the fact that the antiperiplanar arrangement has fewer steric repulsions and a more favourable set of orbital interactions. Namely, 4 σ_C-H/σ*_C-H and 2 σ_C-C/σ*_C-C interactions compared to 2 σ_C-H/σ*_C-H, 2 σ_C-C/σ*_C-H and 2σ_C-H/σ*_C-C . The lowest energy conformation given in the table was Gauche 3. This was then modelled and optimised to give the expected energy of -231.69266 Hartrees. and point group of C₁ .

Gauche 3

It has been suggested that this gauche conformation has the lowest energy is due to two favourable interactions between a vinyl proton and the π orbital of each double bond. The antiperiplanar 2 conformation was then examined in more detail (Anti 2). It's structure was first optimised using Hartree Fock with 3-21G to give a total energy of -231.69254 Hartrees and a point group of C_i . The structure was then optimised again using the B3LYP/6-31G* level which gave a total energy of -234.61170 HArtrees. This is significantly lower than that obtained through Hartree Fock suggesting that, in the case if this molecule, the B3LYP method is more efficient at optimising the structure. This is potentially due to the fact that the dihedral angle after the Hartree Fock optimisation was 179.987^o whereas after B3LYP it was the ideal 180.00^o. A frequency calculation was then performed to obtain thermochemical data and a simulated IR spectrum.

IR Spectrum

Anti 2

Thermochemical Data for anti2-1,5-hexadiene

Energy	Value (Hartrees)	Literature Value (Hartrees)
Sum of electronic and zero point energies	-234.46921	-234.469203
Sum of electronic and thermal energies	-234.46186	-234.461856
Sum of electronic and thermal enthalpies	-234.46091
Sum of electronic and thermal free energies	-234.50078

The energies calculated match well with the provided literature values suggesting that the calculations have been completed correctly.

Optimising the Chair and Boat Transition structures

The Hartree Fock method with a 3-21G basis set was used to optimise two C₃H₅ fragments. These were then used to produce a rough estimate of the transition state for the Cope rearrangement, with the end carbon atoms 2.2 Å apart. This starting estimate was then used to model two transition states, the chair and the boat. The first transition state modelled is the chair. This was subjected to a Berny transition state analysis. Energy = -231.61932 Hartrees, Stretching frequency = 817.91 cm^-1 (imaginary).

This same chair transition state was then optimised using the freeze coordinate method with a redundant coordinate editor and the HF/3-21G optimisation. Energy = -231.62661 Hartrees This fixed the terminal carbon atoms at a distance of 2.2 Å apart ready for the next optimisation. This used the Hessian modification on the carbon-carbon bonds to be broken and formed of the previously optimised structure. Energy = -231.61526 Hartrees, the C-C distances set to 2.20 Å were optimised to 2.02 Å.

The chair transition state was then modelled by the Intrinsic Reaction Coordinate (IRC) method. This works by taking "steps" away from the structure until it finds a minimum energy. In this case, 45 of these steps were needed to find the lowest energy conformation at -231.69161 Hartrees.

IRC Path

(IRC minimum structure)

IRC miminum structure

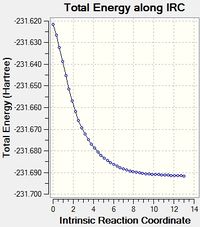
To examine the boat transition state, the QST2 method was used. This uses both a reactant and product structure to calculate the transition state for the rearrangement. In order to prevent the calculation from failing previously optimised structures were carefully arranged and labelled so that they matched each other .This was highlighted by an initial calculation which failed. The transition state optimisation using the QST2 method gave a boat structure. (Boat TS) with an energy of -231.60280 Hartrees. This structure had an imaginary vibration at 839.96 cm^-1 with a terminal C-C separation of 2.14 Å.

Boat TS Vibration

Both the boat and chair transition states were then optimised further using the B3LYP/6-31G* technique. For the chair, freeze coordinate had to be used to prevent the two fragments from moving away from each other, more than 2.2 Å apart. Energy of Chair = -234.554681 Hartrees, Energy of Boat = -234.54309 Hartrees. This shows that the chair is lower in energy than the boat transition state. As with the previously example the B3LYP/6-31G* method optimised to a lower energy than HF/3-21G.

Boat TS

Chair TS

Using the antiperiplanar 2 conformation of 1,5-hexadiene that was used to build the fragments the activation energies can be calculated.

Activation Energies of the Chair and Boat Transition States

Transition State	Energy (Hartrees)	Activation Energy (Hartrees)	Activation Energy (kcal/mol)	Literature Values	Experimental Values
Chair (HF) 0K	-231.53870	0.00085	0.53338	45.70	33.05
Boat (HF) 0K	-231.53949	0.00006	0.03765	55.60	44
Chair (B3LYP) 0K	-234.41493	0.05428	34.06122	34.06	33.05
Boat (B3LYP) 0K	-234.40234	0.06687	41.96157	41.96	44
Chair (HF) 298.15K	-231.53179	0.00391	2.45356	44.69	33.05
Boat (HF) 298.15K	-231.53265	0.00305	1.91390	54.76	44
Chair (B3LYP) 298.15K	-234.40901	0.08285	51.98917	33.17	33.05
Boat (B3LYP) 298.15K	-234.39601	0.07320	45.93370	41.32	44

The energies at 0K are given by the electronic and zero point energies and at 298.15K by the electronic and thermal energies. These energies were obtained from frequency calculation run at both the HF/3-21G and B3LYP/6-31G*.

Energies of Anti 2 Reactant

Energy	Value (Hartrees)
HF 0K	-231.53955
HF 298.15K	-231.5357
B3LYP 0K	-234.46921
B3LYP 298.15K	-234.49186

The values obtained from Hartree Fock are much further (much smaller values) from the literature and previously calculated values than the B3LYP level. This also supports the idea that the B3LYP is a more efficient method of optimisation than Hartree Fock.

The Diels Alder Cycloaddition

The Diels-Alder reaction is a [4+2] cycloaddition between a diene and a dienophile. In this section, a variety of these reactions will be modelled to investigate the nature of the transition state and the stereoselectivity of the reaction. An examination of the molecular orbitals and their interactions will be used to explain the results.

Optimising cis-butadiene

A cis butadiene fragement was optimised using the semi-empirical AM1 basis set. Energy = 0.04889 a.u. . The HOMO and LUMO were also visualised and their symmetries examined. The surface modelled shows that the HOMO is antisymmetric and the LUMO is symmetric. The structure was then re-optimised using Hartree-Fock and B3LYP to give energies of -154.05514 and -155.98649 Hartrees respectively.

Optimised cis-butadiene

Visualisation of MOs of cis-butadiene

HOMO	HOMO	LUMO	LUMO

Transition State and Reaction Path

A transition state structure for the cycloaddition of cis-butadiene and ethene was modelled and optimised using QTS2 with a semi empirical AM1 basis set. The cis-butadiene and ethene were optimised individually and then combined to form the reactant. The distance between the terminal carbon atoms, where the new bond is formed, was set to 2.2 Å. A cyclohexene molecule was modelled, optimised and set as the product. The transition state produced was then optimised using B3LYP/6-31G* to give an energy of -234.63915 Hartrees.

Visualisation of MOs of Diels Alder Transition state

HOMO	HOMO	LUMO	LUMO

Visualisation of MOs of ethene

HOMO	LUMO

The HOMO of the transition state is antisymmetric and the LUMO is symmetric. The HOMO appears to consist of an interaction between the HOMO of the butadiene and the LUMO of ethene, the reverse is true of the transition state LUMO. The reaction is allowed because the butadiene HOMO and the ethene LUMO can overlap mostly in phase, with more bonding interation than antibonding. There is a total of 6 electrons, so fits 4n+2, and the reaction proceeds suprafacially.

The distances between the terminal carbons of the ethene and cis-butadiene are 2.12 Å. A typical C-C bond has a length of 1.54 Å whereas a C=C is around 1.34 Å. The Van der Waals radius of a carbon atom is around 1.7 Å, so these interactions are very weak.However, the separation is less than twice the Van der Waals radius so orbital overlap can occur and there will be interactions of some sort. The formal C=C bonds of the starting butadiene and ethene are 1.38 Å in the transition state.

Reactants	Products	Transition State	Imaginary Vibration	IRC final structure
			click for animation

The transition state had an imaginary vibrational frequency at 956.16 cm^-1. The vibration suggests that the formation of the new bonds is synchronous. The lowest positive vibration is at 147.2 cm^-1 which describes an asynchronous twisting of the ethene molecule relative to the butadiene. There is no real manipulation of the bonds here which is probably why it has such a low energy. The final IRC step, the 19th, has a fully formed ring structure which suggests that the calculated transition state is actually the transition state for the cycloaddition. The final IRC structure has C-C bond lengths of 1.51 Å, shorter than the 2.12 Å of the transition state and within the Van Der Waals radii of a carbon atom. This suggests that they are strong bonding interactions.

Study of Regioselectivity

Two transition states, endo- and exo-, for the Diels Alder cycloaddition of cyclohexa-1,3-diene with maleic anhydride were optimised using the QST2 method. The reactants were drawn and optimised using the AM1 semi-empirical method as well as two possible products, the endo- and exo-forms. To create the inital guess transition state the C=C of maleic anhydride was placed 2.2 Å away from the relevant carbon atoms of the cylohexadiene.

Endo

Product	Transition State	Imaginary Vibration	HOMO	LUMO	Dihedral Angle of Maleic Anhydride Relative to Ring
		click and full res for animation			176.8o

Exo

Product	Transition State	Imaginary Vibration	HOMO	LUMO	Dihedral Angle of Maleic Anhydride Relative to Ring
		click and full res for animation			56.0o

Steric Data for Endo- and Exo-products

Conformation	Partly formed σ C-C length (Å)	Distance between C(O)OC(O) and opposing group (Å)	Total Energy	Sum of Electronic and Zero Point Energies (0K)	Sum of Electronic and Thermal Energies (298.15K)
Endo AM1	2.16	2.89	-0.05150	-0.133495	-0.143684
Exo AM1	2.17	2.95	-0.05042	-0.134880	-0.144881
Endo B3LYP	1.56	2.99	-612.75829	-612.491204	-612.481444
Exo B3LYP	1.56	2.99	-612.75578	-612.486689	-612.476968

The imaginary vibrational frequency for the endo form is 806.4 cm^-1 and for the exo is 812.2 cm^-1. The energy of the endo transition state is -0.05150 a.u. and the exo is -0.05042 a.u.for the inital AM1 basis set. This shows that the endo transition state is lower in energy and therefore likely to be preferred thermodynamically. This is also true for the structures optimised through the B3LYP/6-31G* method.

It has been suggested that the endo configuration is stabilised through Secondary Orbital Overlap Effects. These are favourable interactions in the non-active frame i.e. away from where bonds are broken and formed. These take place between the diene HOMO and the LUMO of the dienophile. In this example, specifically between the C=C and the C(O)-O-C(O) unit of the maleic anhydride component. The MO visualisation shows that there is more orbital overlap between the maleic anhydride component and the 6 membered ring in the endo arrangement. This may well be due to these favourable secondary orbital interactions which lowers the energy of the endo configuration. This overlap isn't present to the same extent in the exo arrangement where there is more "dead space" between the anhydride and the cyclohexene ring orbitals.

The exo form also suffers from repulsive interactions between the -CH₂-CH₂- of the "bridge" and the C(O)-O-C(O) unit of the maleic anhydride. Although further apart than the favourable interactions in the endo form, they are still within twice the Van der Waals' radius of a carbon atom so an interaction can take place.

Conclusion

A range of methods including Berny, QTS2, frozen coordinate and the Hessian operator were used to model the chair and boat transition states for the Cope rearrangement of 1,5-cyclohexadiene. QST2 was then used to model the transition state for a Diels Alder reaction and the appropriate molecular orbitals were examined. Finally, the QST2 method was used to examine the regioselectivity of the reaction of maleic anhydride with 1,3-cyclohexadiene. This showed that the endo product is favoured over the exo with examination of the MOs suggesting that this may be due to the Secondary Orbital Overlap Effect.

An interesting area of further study would be to examine the reaction with asymmetric dienes and dienophiles and investigate the regioselectivity. If a range of electron withdrawing and donating groups were used this could give an insight into electronic and MO requirements of the reaction.