Rep:Mod:APP842Backup
NH3 Molecule
The N-H optimised bond distance is 1.02 Angstroms The N-H optimised angle distance is 106 degrees
The molecule is NH3, ammonia
The Calculation Method is RB3LYP
The Basis Set is 6-31G(d,p)
The final energy (E(RB3LYP)) is -56.55776873 au
The RMS Gradient Norm is 0.00000485
The Point Group is C3V
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Jmol Image of NH3
test molecule |
The optimisation file is linked to here
NH3 Vibrations
| Wavenumber cm-1 | 1090 | 1694 | 1694 | 3461 | 3590 | 3590 |
| Symmetry | A1 | E | E | A1 | E | E |
| Intensity arbitrary units | 145 | 14 | 14 | 1 | 0 | 0 |
From the 3N-6 rule, 6 modes of vibration are expected, as found.
The two vibrations at 1694 cm are degenerate as well as the two at 3590 cm.
The three vibrations with the lowest wavenumber frequency (1090,1694 and 1694) are bending vibrations and the three highest are "bond stretch" vibrations (3461,3590 and 3590)
The mode at 3461 cm is highly symmetric.
The "umbrella" mode is the one at 1090 cm.
I would expect to see either three or four bands depending on the precision of the apparatus since two of the modes have an intensity of nearly zero. The degenerate modes give rise to one band.
Charge analysis
The charge found when using the NBO charge distribution was of -1.125 for Nitrogen and +0.375 for each Hydrogen
These results are in accord with expectations since Nitrogen has an electronegativity value of 3 (add ref) and Hydrogen of 2.1. Therefore, the bond is polarised covalent towards the nitrogen, which bears more of a negative charge due to its higher electronegativity.
N2Molecule
The N-N optimised bond distance is 1.11 Angstroms
The molecule is N2, molecular nitrogen.
The Calculation Method is RB3LYP
The Basis Set is 6-31G(d,p)
The final energy (E(RB3LYP)) is -109.52412868 au
The RMS Gradient Norm is 0.00000365
The Point Group is DinfH.
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000002 0.001800 YES RMS Displacement 0.000003 0.001200 YES
Jmol Image of N2
test molecule |
The optimisation file is linked to here
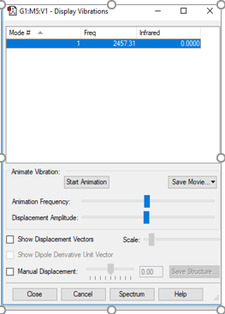
N2 Vibrations
| Wavenumber cm-1 | 2457 |
| Symmetry | SGG |
| Intensity arbitrary units | 0 |
Charge analysis
The charge found when using the NBO charge distribution was of 0.000 for each of the Nitrogen atoms.
This is in complete agreement with expectations since the bond is purely covalent, both atoms are the same.
Conquest Complex for N2
The unique identifier of the molecule is NAWKED with the following link https://www.ccdc.cam.ac.uk/structures/Search?Ccdcid=NAWKED&DatabaseToSearch=Published
The bond length found in the crystalline structure is of 1.107(±0.004) Angstroms while the one measured on the gaussian optimisation software was of 1.11 Angstroms. Although the value found is within the literature range, there seems to be a slight shortening of the bond length. This is in contradiction with MO theory since the end-on bond between Nitrogen and Cobalt would promote electrons in the LUMO, which is the pi star antibonding orbital, therefore decreasing bond order and increasing bond length. The main reason this is not observed is because both values are not measured in the same conditions; one measurement is an experimental observation whilte the other is a computational simulation. There is bound to be differences, which is why a lengthening of the bond is not observed. Firstly, the computational method is inevitably going to be an approximation of the real situation because approximations have to be made to solve the Schrodinger equation. Specifically, the calculation method is RB3LYP and the basis set is 6-31G(d,p), which calculates six wavefunctions. The ideal case would be an infinite amount of wavefunction calculations. Furthermore, the solvent in the crystalline structure can also affect the bond length measured experimentally by compresssing the bond.
H2 Molecule
The H-H optimised bond distance is 0.74 Angstroms
The molecule is H2, molecular hydrogen.
The Calculation Method is RB3LYP.
The Basis Set is 6-31G(d,p)
The final energy (E(RB3LYP)) is -1.17853930 au
The RMS Gradient Norm is 0.00012170
The Point Group is DinfH.
Item Value Threshold Converged? Maximum Force 0.000211 0.000450 YES RMS Force 0.000211 0.000300 YES Maximum Displacement 0.000278 0.001800 YES RMS Displacement 0.000393 0.001200 YES
Jmol Image of H2
test molecule |
The optimisation file is linked to here
H2 Vibrations
| Wavenumber cm-1 | 4461 |
| Symmetry | SGG |
| Intensity arbitrary units | 0 |
Charge analysis
The charge found when using the NBO charge distribution was of 0.000 for each of the Hydrogen atoms.
This is in complete agreement with expectations since the bond is purely covalent, both atoms are the same.
Haber Bosch Process
E(NH3)= -56.55776873 2*E(NH3)= -113.11553746 E(N2)= -109.52412868 E(H2)=-1.17853930 3*E(H2)=-3.53561808 ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 a.u. ΔE=-146.47901911 kJ/mol
Because the difference in energy between the products and reactants is negative, the ammonia product is more stable than the gaseous reactants.
O2 molecule
The O-O optimised bond distance is 1.21602 Angstroms
The molecule is O2, molecular oxygen.
The Calculation Method is RB3LYP
The Basis Set is 6-31G(d,p)
The final energy (E(RB3LYP)) is -150.25742434 au
The RMS Gradient Norm is 0.00007502
The Point Group is DinfH.