Rep:Mod:AO1995

Introduction

The transition state of a chemical reaction is the point of highest energy(the least stable point)during the reaction. In other words, It is the point at which the first derivative of potential energy surface is equal to 0 and the second derivative is less than 0. These structures cannot be experimentally determined but can be modeled using computational methods. There are various approaches and levels of theory that can be used. Modelling a system is a comprise between the level of accuracy and how computationally expensive it is. Three different reaction were investigate:the Cope Rearrangement of 1,5-hexadiene and Diels alder reactions. Three different level of theory were used. AM1 semi empirical which was the least accurate method as the atomic orbital basis set is not specified. HF which is computationally more expensive as it requires solving many electron wave function via slater determinants. The most accurate method used was DFT which uses functionals of the electron density to obtain the optimised structure.

Nf710 (talk) 12:07, 17 December 2015 (UTC) This is an acceptable level of understanding

The Cope Rearrangement

Background

The cope rearrangement of 1,5-hexadiene undergoes a [3,3]-sigmatropic shift rearrangement which is concerted[1].This can proceed either via a boat or chair transition state.

Optimisation of 1,5-hexadiene conformers at HF/3-21G level of theory.

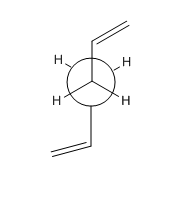
1,5-hexadiene with an"anti"linkage,where the two alkene groups are antiperiplanar to each other as shown from the newman projection in figure 1, was drawn in gaussview by setting the dihedral angle to 180^o The molecule was then optimised with HF/3-21G level of theory. The energy and point group were found to be -231.69253528 a.u and Ci which corresponds to anti2 in the appendix.

The "Gauche" conformer of 1,5-hexadiene was drawn in Gaussview by setting the dihedral angle to 60 ^o.Again, this conformer was optimised with HF/3-21G level of theory. The energy point group were found to be -231.69266120 a.u and C₁ respectively. This corresponds to gauche3 in the appendix 1.

One may expect that the most stable conformer to be the anti 1,5-hexadiene conformer . However, the most stable conformer was shown to be the gauche linkage conformer which is due to favourable interactions between both of the $\pi$ orbitals resulting in a greater stabilisation compared to the anti. It can be seen from the HOMO of the gauche conformer that there is secondary orbital interaction between the two $\pi$ bonds whereas the anti does not have that interaction therefore the stabilization lowers the energy.

Figure 6:The HOMO molecular orbital of the anti conformer of 1,5 hexadiene at HF/3-21G level of theory

Figure 7:The HOMO molecular orbital of the gauche conformer of 1,5 hexadiene at HF/3-21G level of theory

Nf710 (talk) 12:12, 17 December 2015 (UTC) great use of orbitals to explain your theory, but perhaps this would have been better to go after the part where you worked out the energy.

Optimisation of "anti2" 1,5-hexadiene at B3LYP/6-31G* level of theory.

The optimisation of anti conformer was done with the B3LYP/6-31G* basis set. The energy was found to be -234.61171063 The point group remains the same but the energies are different due to the different basis sets used and hence cannot be compared. The log file can be found here.

The numbering of atoms is shown from the image below. Both basis sets used had the same point group(Ci) indicating that the overall geometry remains practically the same. However, a few difference were observed.

Conformer	Optimised structure	Level of theory	Point group	Energy/ Hartrees	Relative Energy/Kcal/mol	Log file
Anti periplanar		HF/3-21G	C1	-231.69253528	0.08	anti
Gauche		HF/3-21G	Ci	-231.69266120	0.00	gauche
Anti periplanar		B3LYP/6-31G*	Ci	-234.61171063	-	anti1

	Bond Lengths (Å)
Atoms	B3LYP/6-31G*	HF/3-21G
C1-C2	1.33350	1.31613
C2-C3	1.50419	1.50891
C3-C4	1.54816	1.55275

The singles bonds for the B3LYP/6-31G* basis set used appear to be longer than the HF/3-21G (C2-C3 and C3-C4) . The double bond appears to be shorter and closer to the literature value of 1.33 Å in the case of B3LYP/6-31G* (C1-C2) compared to HF/3-21G basis set used indicating that B3LYP/6-31G* models the system more accurately.

	Dihedral Angle (°)
Atoms	B3LYP/6-31G*	HF/3-21G
C2-C3-C4-C5	180	180

The dihedral angle between C2-C3-C4-C5 should be 180° as the two alkene groups are anti to each other. Both basis sets were consistent with this value.

	Angle (°)
Atoms	B3LYP/6-31G*	HF/3-21G
C2-C1-H15	121.86525	121.86752
C2-C1-H16	121.65898	121.82269
H15-C1-H16	116.47521	116.30950

Since C2 atom is $s{p}^2$ hybridised ,the angle for C2-C1-H15 , C2-C1-H16 , H15-C1-H16 should be 120°. It can be seen that for B3LYP/6-31G* that these values are closer compared to HF/3-21G used.

Overall, it can be seen that the geometry is almost the same for both basis sets used but the B3LYP/6-31G* basis set is slightly more accurate than HF/3-21G.

Nf710 (talk) 12:16, 17 December 2015 (UTC) good geometry comparison

Frequency analysis of an anti 1,5-hexadiene conformer

All of the vibrations were positive and no imaginary frequencies were present indicating that the structure was successfully optimised. The presence of an imaginary frequency is characteristic of the transition state.This occurs the 2nd derivative is a negative value( maximum provided 1st derivative is 0) implying a negative force constant due to the relationship as shown by the following quantum harmonic oscillator equation: $\nu {c{m}^{-1}}_{}=\frac{1}{2\pi c}\sqrt{\frac{k}{\mu }}$ where c represents the speed of light in Cm s^-1, k represents the force constant in gs^-2, and μ the reduced mass in grams. The log file can be found here It is also possible to obtain the thermochemistry data which is shown in the following table.

Energetic Values
Sum of Electronic and Zero-point Energies at 0 K	-234.469219
Sum of Electronic and Thermal Energies at 298.15 K	-234.461869
Sum of Electronic and Thermal Enthalpies	-234.460925
sum of Electronic and Thermal Free Energies	-234.500809

The sum of electronic and zero-point energies at 0 K refers to the sum of the electronic potential energy and the zero point energy in the system The sum of electronic and thermal energies at 298.15 K at 1 atm is a sum of the electronic,translational,rotational and vibrational energies. The sum of electronic and thermal enthalpies contains a RT correction term(H = E + RT). The sum of electronic and thermal free energies contains an entropic contribution (G = H - TS).

12:20, 17 December 2015 (UTC) Good understanding of the theory behind the imaginary frequencies and thermochemistry, although the speed of light should defiantly not be there.

Optimisation of allyl fragment

In order to make the transition states of the chair and boat conformation, it is possible to build the transition state from smaller fragments and so an ally fragment was used. This was optimised with the HF/3-21G basis set. and the file can be found here

Optimised Structure	Level of Theory	Point Group	Energy/ Hartrees
	HF/3-21G	C2v	-115.82304010

Optimisation of 1,5-hexadiene Chair Transition State by using TS Berny Method and HF/3-21G theory (Guess method)

The Transition state was built by placing an optimised ally fragment on top of another ally fragment in a 'staggered' conformation.The distance between the terminal carbons of the allyl fragments was set to 2.2 Å . The structure was then optimised using the Berney algorithm The results are summerised below and the log file can be found here.

Optimised Structure	Level of Theory	Point Group	Energy/ Hartrees	Imaginary frequency/cm-1
	HF/3-21G	C1	-231.61932242	-817.93

A imaginary frequency was found with a wavenumber of-817.93^-1 indicating that the transition state is formed. The vibration is shown below.

Animation of imaginary frequency

Optimisation of 1,5-hexadiene Chair Transition State by using frozen coordinate method and HF/3-21G theory

The chair conformation can also be optimised by another method called the frozen coordinate method. The structure was optimised with HF/3-21G where the distances between the terminal carbons of the allyl fragments were fixed to 2.2 Å(where the bonds break and form ). This means that the optimisation proceeded with the terminal carbons being fixed while the rest of the molecule is optimised. The terminal carbons were then unfixed and the whole molecule was reoptimised. The optimised file can be found here.

Optimised Structure	Level of Theory	Point Group	Energy/ Hartrees	Imaginary frequency/cm-1
	HF/3-21G	C1	-231.61932233	-817.89

A imaginary frequency was found with a wavenumber of-817.93^-1 indicating that the transition state is formed. The vibration is shown below.

Animation of imaginary frequency

Method	Bond breaking length/Å	bond forming length/Å
Guess with berney	1.38927	2.02055
Frozen coordinate	1.38929	2.02076

Both methods provide very similar energies,bond lengths and imaginary frequencies indicating that both methods can obtain reasonable results. however the Guess method is highly depended on how well the initial structure is drawn so the frozen coordinate method is more reasonable to use.

Optimisation of 1,5-hexadiene boat Transition State by using QST2 method and HF/3-21G theory

A different method,QST2, is used to optimise the boat transition structure. The transition state is obtained by interpolating between the reactant and product. The labelling of the reactant and product is shown below.

Labelling of reactant	labelling of product

Intially,the anti 2 structure which was used as both the product and reactant from appendix 1 was optimised with HF/3-21G using the QST2 method. However, this lead to a transition structure that was highly unfavorable which is shown below.

In order to obtain the correct geometry for the reactant and product, the following torsion angles were applied :C2-C3-C4-C5 was set to 0° in the reactants,C5-C6-C1-C2 was set to 0° in products.Also the following angles were applied: C2-C3-C4 and C3-C4-C5 were set to 100° in the reactant, C5-C6-C1 and C6-C1-C2 were set to 100° in the product . This was then optimised with HF/3-21G using the QST method.The optimisation and frequency output log file for the successful boat transition structure can be found here.

Optimised Structure	Level of Theory	Point Group	Energy/ Hartrees	Imaginary frequency/cm-1
	HF/3-21G	Cs	-231.60280200	-839.94

A imaginary frequency was found with a wavenumber of-839.94^-1 indicating that the transition state is formed. The vibration is shown below.

Animation of imaginary frequency

Nf710 (talk) 12:28, 17 December 2015 (UTC)All your frequencies are correct here and good use of jmols! very nice comparison of geoms too.

Intrinsic reaction coordinate of chair and boat transition structure at HF/3-21G (IRC)

In order to confirm that the transition structure has been correctly optimised , It is necessary to check whether or not the reaction path from the transition state goes to both minima in both directions(reactants and production). IRC preforms a series of optimisations on the constrained geometries along the reaction path (steepest decent which is from the transition state to the reactants and products)

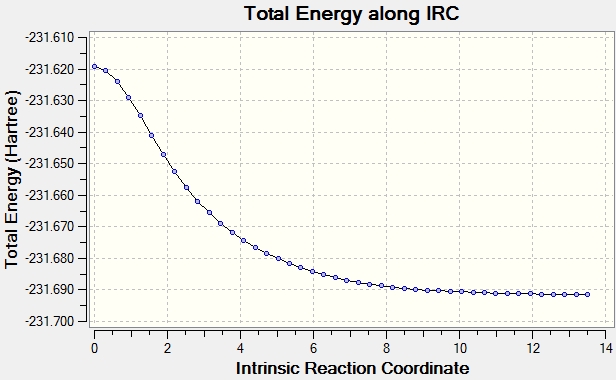
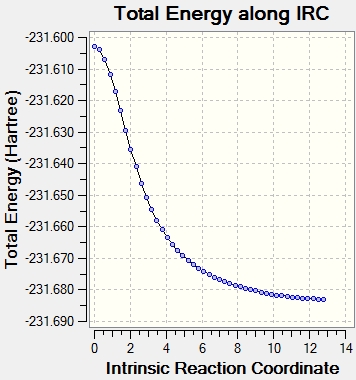
The chair transition structure was optimised with HF/3-21G with and IRC. The reaction coordinate was calculated in the forwards direction only because the reaction coordinate is symmetric. The number of points that were monitored was set to 50. The log file can be found here. The boat IRC can be found here

Chair	Boat

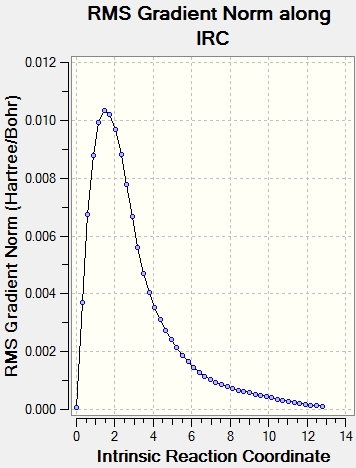
It can be seen from the plots of the total energy vs IRC that the energy is initially at it's peak(the transition state) and then decreases till the total energy does not change(reactant/product as the PEs is symmetrical in this case). On the otherhand, the RMS plot displays how the 1st derivative of the total energy varies with IRC.

Nf710 (talk) 12:31, 17 December 2015 (UTC) Good understanding of the IRC method, however you didn't try to identify why conformer it connects, this could have been done by reoptimising the final structure or doing an IRC with force constants computed at every step

Optimisation of chair and boat transition state at B3LYP/6-31G*

The Boat and Chair transition state was optimised at a higher level of theory using B3LYP/6-31G*. The results are summerised below and the log files can be found here Boat Chair

Optimised Structure	Level of Theory	Point Group	Energy/ Hartrees	Imaginary frequency/Cm^-1
	B3LYP/6-31G*	C2h	-234.55698303	-565.54

Optimised Structure	Level of Theory	Point Group	Energy/ Hartrees	Imaginary frequency/Cm^-1
	B3LYP/6-31G*	C2v	-234.54309307	-530.30

Results Table

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies at 0 K	Sum of electronic and thermal energies at 298.15 K	Electronic energy	Sum of electronic and zero-point energies at 0 K	Sum of electronic and thermal energies at 298.15 K
Chair TS	-231.61932242	-231.466700	-231.461341	-234.55698303	-234.414929	-234.409009
Boat TS	-231.60280200	-231.450928	-231.445299	-234.54309307	-234.402343	-234.396008
Reactant (Anti2)	-231.69253528	-231.539539	-231.532565	-234.61171063	-234.469219	-234.461869

	HF/3-21G		B3LYP/6-31G*		Experimental.
	0 K	298.15 K	0 K	298.15 K	0 K
ΔE (Chair)/kcal/mol	45.71	44.71	34.07	33.17	33.5 ± 0.5
ΔE (Boat)/kcal/mol	55.60	54.76	41.97	41.33	44.7 ± 2.0

The point group for both basis sets used did not change indicating that both basis sets used describes the geometry reasonably well.It can be seen from the table above that using B3LYP/6-31G* provides values that are closer to the experimental literature. As a result ,using HF will provide reasonable results for geometry. however, In order to obtain an accurate value for the energy, A higher level of theory must be used i.e DFT. The activation energies were determined by look at the thermochemistry data which is shown in the first table. The second table shows the conversion to kcal/mol. The activation energy is calculated by finding the energy difference between the reactants and the transition state energy.

The large discrepancy in energy between the HF and DFT method arises from the difference in the how the methods work. HF desribes the system by solving many electron wave functions using slaters determinant. This does fullytake into account the electron-electron interactions hence the energies tend to be higher which is consistent with the data. DFT on the other hand includes these Coulombic interactions.

Nf710 (talk) 13:51, 17 December 2015 (UTC) your energies are very good. well done. you could have looked at the geoms to see tat lower basis sets are still pretty good at working out the energy. Other than that your report is pretty good you have most of the stuff asked of you however you could have taken things a bit further with your understanding of the theory.

Diels alder cycloaddtion

Background

Diels-Alder cyclo additions are a class of pericyclic reactions where two sigma bonds are formed and one pi bond is broken.

Optimisng cis butadiene with AM1 level of theory

Cis butadiene was optimised with the AM1 empirical level of theory. The data is summerised in the following table and the log file for the optimisation can be found here

Optimised Structure	Level of Theory	Point Group	Energy/ Hartrees
	AM1	C2v	0.04879719

(Throughout this section you've uploaded jmols but haven't included the script to display the optimised model. This means you're only displaying the starting geometry. Use <script>frame FRAMENUMBER</script> where FRAMENUMBER is the number of the optimised geometry Tam10 (talk) 16:48, 10 December 2015 (UTC))

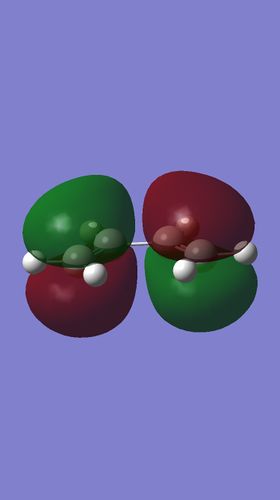
The Homo and Lumo of cis butadiene is shown below.

HOMO	LUMO
The HOMO is antisymmetric with respect to the plane	The LUMO is symmetric with respect to the plane

Optimising ethene with AM1 level of theory

Ethene was optimised with the AM1 empirical level of theory. The data is summerised in the following table and the log file for the optimisation can be found here

Optimised Structure	Level of Theory	Point Group	Energy/ Hartrees
	AM1	D2h	0.02619024

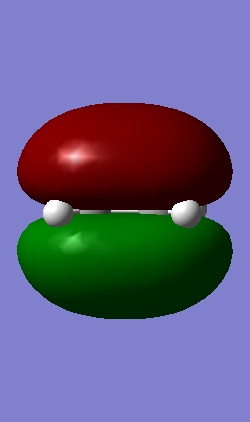
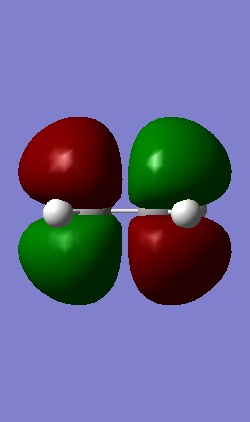
The Homo and Lumo of ethene is shown below.

HOMO	LUMO
The HOMO is symmetric with respect to the plane	The LUMO is antisymmetric with respect to the plane

Optimisation of the ethylene+cis butadiene transition structure

The transition structure was constructed by first building a bicyclo[2,2,2]octane and then removing -CH2-CH2- fragment. The distance between the carbons where sigma bonds are formed are set to 1.5Å. This structure was then optimised with AM1 semi-empirical molecular orbital method using TS berney. The data is summerised in the following table and the log file for the optimisation can be found here

This was also optimised with B3LYP/6-31G* and the log file can be found here

Optimised Structure	Level of Theory	Imaginary frequency/ cm-1	Energy/ Hartrees
	AM1	-956.15	0.11165465

Optimised Structure	Level of Theory	Imaginary frequency/ cm-1	Energy/ Hartrees
	B3LYP/6-31G*	-525.36	-234.54389742

The imaginary frequency vibration corresponding to reaction path at the transition state is shown below.

Animation of imaginary frequency

The vibration shows that the formation of the bonds are synchronous as the vibration shows both bonds being formed at the same time.

The lowest positive frequency was calculated to be 177.19 cm^-1 The vibration of the lowest positive frequency is shown below.

Animation of imaginary frequency

The vibration appears to not have any relation to the formation of the sigma C-C bonds as the vibration does not occur in the direction of where the bonds are formed.

The Homo and Lumo of ethylene+cis butadiene transition structure is shown below.

HOMO	LUMO
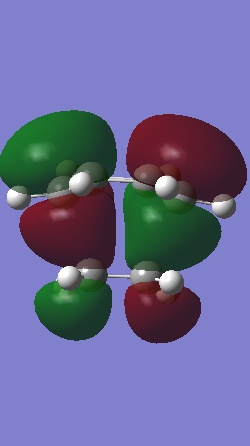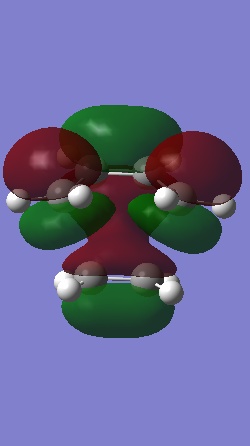
The HOMO is antisymmetric with respect to the plane	The LUMO is symmetric with respect to the plane

The HOMO of butadiene and LUMO of ethene were used to form this transition structure MO.This was deduced by making a direct comparison between the MO of the reactants and the transition structure. Using the woodward Hoffman rule, It can be deduced that both the ${\pi }^4$ and${\pi }^2$ components react in a superfacial manner and hence this reaction is thermally allowed.

(You should go into a bit more depth about the Woodward-Hoffman rules, especially noting the symmetry Tam10 (talk) 16:48, 10 December 2015 (UTC))

The labelling of the transition structure uses the following labels:

Atom	AM1 Bond Lengths (Å)	6-31G* Bond Lengths (Å)
C10-C3	2.11922	2.27222
C7-C2	2.11935	2.27222
C7-C10	1.38290	1.38601
C1-C2	1.38184	1.38306
C1-C4	1.39749	1.40715
C3-C4	1.38185	1.38306

The typical C-C bond length for sp3 and sp2 are 1.54[2] and 1.46[3] Å respectively while the Van der waals radius is 1.7 Å[4]. For both levels of theory, the distance between the carbons where the bonds are formed is less than 3.4 Å( 2 times the van der waals radius) indicating that there is an attractive interaction leading to the sigma bond formation which is consistent with the reaction.

The bond lengths are approximately the same for both basis set used. However, the partly formed sigma C-C bond differ by approximately 0.16 Å.

Exo Transition State Optimisation

The transition state was optimised with both AM1 using the QST2 method. The log files of the optimsation can be found here. AM1

Optimised Structure	Level of Theory	Imaginary frequency/ cm-1	Energy/ Hartrees	HOMO	Relative energy(kcal/mol)
	AM1	-812.32	-0.05041976		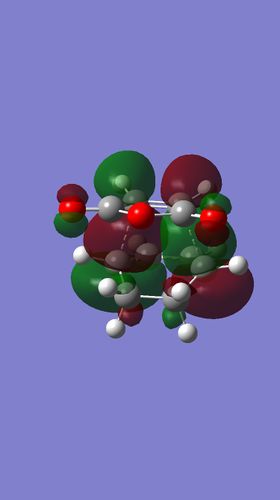1

(Did you mean "0" for the relative energy in kcal/mol? Tam10 (talk) 16:48, 10 December 2015 (UTC))

Endo Transition State Optimisation

The transition state was optimised with both AM1 using the TS berney method. The log file of the optimsation can be found here. AM1

Optimised Structure	Level of Theory	Imaginary frequency/ cm-1	Energy/ Hartrees	HOMO	!Relative energy(kcal/mol)
	AM1	-812.32	-0.05041976		0.68

(Watch out here: you've copied the table across and forgot to update the energy and imaginary frequency

Comparsion between endo and exo

The following numbering is used for the exo transition structure.

Atom	AM1 Bond Lengths (Å)
C6-C17(partly formed σ C-C bond)	2.17027
C15-C3 (partly formed σ C-C bond)	2.17038
C2-C20	2.94494
C19-C1	2.94543
C17-C18	1.41012
C6-C5	1.39440
C5-C4	1.39677
C4-C1	1.39437

The following numbering is used for the endo transition structure.

Atom	AM1 Bond Lengths (Å)
C3-C17(partly formed σ C-C bond)	2.16225
C15-C6 (partly formed σ C-C bond)	2.16249
C6-C20	2.83099
C19-C4	2.89206
C17-C18	1.40850
C3-C3	1.39308
C5-C4	1.39722
C5-C6	1.39304

The partially formed is slightly longer for exo and the distance between the carbonyl carbon and the "opposite" carbon appears to be longer for exo. This suggests that there is some steric effect that makes these distances longer. One of the contributons may stem from the H11 and H8 as they point towards the Maleic anhydride in the exo(sp3 hydrised adjacent carbon centre where as the endo has an sp2 hybrised centre).

(The contributions from H11 and H8 are probably the most significant for the steric effects. These values should be in the table too, really Tam10 (talk) 16:48, 10 December 2015 (UTC))

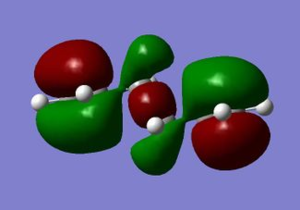
The Secondary orbital overlap effect refers the interaction between orbitals that do not directly participate in the bond forming and breaking in the reaction[5].The HOMO of the Endo transition structure shows very little interaction between (C=O)-O-(C=O) and the diene. The overlap with the rest of the molecule is practically non existent. However, there may be contributions from the through space interaction although it is very weak. This indicates that the reason as to why the transition state is lower in energy is due to predominately due to sterics and not the secondary orbital effect in this optimisation. The lack of Secondary orbital effects may be due to the low level of theory used .

(This is fair enough. The secondary orbital overlap is far too subtle with this level of theory (especially when defining the iso value as 0.02 Tam10 (talk) 16:48, 10 December 2015 (UTC))

Conclusion

In conclusion, the use of computational methods can be used to predict the transition structure and provide greater insight as to how the reaction proceeds by analysis the MOs. Various transition structures of different reactions were examined as a result it was possible to deduce favorable reaction pathways and activation energies.

References

1. Cope, A.C., Hardy, E.M.. (1940). The Introduction of Substituted Vinyl Groups. V. A Rearrangement Involving the Migration of an Allyl Group in a Three-Carbon System. J. Am. Chem. Soc. 62 (2), 441-444.

2.Pauling, L. (1931). THE NATURE OF THE CHEMICAL BOND. II. THE ONE-ELECTRON BOND AND THE THREE-ELECTRON BOND. J. Am. Chem. Soc., 53(9), pp.3225-3237.

3.Wang, J. et al. (2013). New Carbon Allotropes with Helical Chains of Complementary Chirality Connected by Ethene-type π-Conjugation. Sci Rep.. 3, 3077.

4.Rowland,R.S et al. (1996). Intermolecular Nonbonded Contact Distances in Organic Crystal Structures: Comparison with Distances Expected from van der Waals Radii. J. Phys. Chem. 100 (18), 7384–7391.

5.Fox, M., Cardona, R. and Kiwiet, N. (1987). Steric effects vs. secondary orbital overlap in Diels-Alder reactions. MNDO and AM1 studies. The Journal of Organic Chemistry, 52(8), pp.1469-1473.