Rep:Mod:AM8709mod2
Module 2: Computational chemistry in Inorganic Chemistry
In this module various classes of inorganic molecules, from a simple compound to a large structure of organometallic species, were investigated using density functional theory or DFT method. In the first section of this module a simple molecule such as borane (BH3) was optimised; its molecular orbitals and infrared (IR) spectrum were simulated in order to get familiar with the softwares, Gaussian 09 and Gaussview 05, as well as to be able to potentially analyse the data obtained from the calculations. After the study of borane, a molecule consisting of heavy atoms, e.g. TlBr3, was analysed using pseudo-potentials and symmetry restriction to help the calculation go more quickly. Then the cis-, trans- isomerisation of the organometallic molecule, Mo(CO)4(PCl3)2, was studied. In the last section of this module is a mini project about the methylation of the ethylimidazole. In the mini project the reactivity of the imidazole is predicted and described by the inspection of the molecular orbitals of the imidazole. The vibrational modes of the reactants and the products of the reaction were compared. Finally, the reaction energy was calculated and discussed whether the reaction is thermodynamically favourable or not.
Borane, BH3
Optimisation of BH3
A BH3 molecule was drawn in Gaussview 05 by the bond lengths of all three B-H bonds were set to 1.50 Å. The molecule was optimised using DFT/B3LYP method with low accuracy type basis set, 3-21G. 3indicates that the core atomic orbital basis functions of the molecule are composed of three primitive gaussian functions; 21G indicates that the valence orbitals of the molecule are made from two basis functions, one of which is formed by the linear combination of two gaussian functions, the other is composed of just one primitive gaussian function. After the results from the optimisation was obtained, first thing that one must check is whether the optimisation was actually successfully done or not. To do this the values of forces and displacements and derivative of energy and displacement must be check as follows.
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
These data are extracted from *.log file obtained after the optimisation. All values of forces and displacements are converged, and also the values for the derivatives (-DE/DX) are less than 0.001 or equal to 0. The data confirm that the optimisation was completed, because the convergence of forces and displacements as well as zero energy/displacement derivatives mean that small change in displacement of the atoms does not lead to a change in energy,i.e. the energy is at a critical point or at the minimum in this case.

Now look at the summary of the results from Gaussview 05. Most of the information in this window are already mentioned, but some are not. From the window, the molecule is neutral as it has zero charge; the total energy of the molecule is -26.462±0.004 Hartree; the root mean square gradient (<-DE/DX>) is 0.0002 (less than 0.001); the molecule is non-polar as the dipole moment is 0.00 Debye; the molecule is in the D3h point group.
Another way to check that the optimisation has reached the minimum point or not is to look at the Total Energy and RMS Gradient Norm graphs. The principal is the same as mentioned earlier that the gradient, -DE/DX, must be close or equal to zero, and the total energy must decrease from the starting point, and also for this particular case the B-H bonds should be shorten during this 5 cycle optimisation due to the fact that at the beginning they were set to 1.50 Å, which are longer than normal.


The structure of the BH3 molecule after the optimisation indicates that the bond lengths for all B-H bonds are 1.19±0.01 Å (lit.[1], 1.19 Å) and all bond angles are 120° (lit.[1], 120°).
From this it can be concluded that for simple structure molecules such as BH3, 3-21G (low accuracy basis set) worked perfectly for the optimisation. In this case if the more accurate basis set was used, the same results would be obtained, but more time would be consumed. Therefore, it is not necessary to use any better basis set for the optimisation of BH3.
Vibrational analysis of BH3
As mentioned earlier, the optimised molecule of BH3 is classified in the D3h point group. The diagram of the symmetry elements for the BH3 molecule is shown below (Housecroft Inorganic Chemistry). Despite the fact that the symmetry of the molecule has changed during the molecular vibration, the vibrational modes in the molecule can be classified using the symmetry labels of the D3h point group, see later on in this section.

The infrared (IR)spectrum of the optimised molecule was calculated in Gaussian 09 using DFT/B3LYP with 3-21G basis set. Once the results of the calculation were obtained, the total energy of the molecule was compared to the total energy of the optimised molecule. These two energies are necessary to be equal as to ensure that the molecule remained the same geometry during the calculation. If they are not equal, it means that the frequencies gained from the computation do not belong to the optimised molecule. The optimised molecule was used as a starting point for the frequency calculation, because small differences in the geometry of the molecule can lead to large shifts of the frequencies.
According to the summary windows of the optimisation and frequency calculations, the energies from both calculation are identical.

Now let us consider the data from the *.log file from the calculation, the six values at low frequencies were observed as shown below in boldface. These values come from the motions of the centre of mass of the molecule, therefore their magnitudes are much smaller than that for the molecular vibrations showing the IR spectrum shown below in underlined. Theses frequencies are usually close to zero, but the reason for that the ones which found in this study are not close to zero is that the low accuracy basis set (3-21G) was used for the calculation. If the better basis set is used, such values will be close or equal to zero.
The peaks showing on the spectrum are expected to be positive as the frequencies are derived from the second derivative of energy and displacement, and at the minimum critical point such a derivative is positive. Otherwise the structure is not at the minimum energy, i.e. it is at the transition state!!!
Low frequencies --- -66.7708 -66.3686 -66.3683 -0.0019 0.0032 0.2122
Low frequencies --- 1144.1479 1203.6412 1203.6422
Diagonal vibrational polarizability:
0.6013540 0.6012840 1.9090976
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A2" E' E'
Frequencies -- 1144.1479 1203.6412 1203.6422
Red. masses -- 1.2531 1.1085 1.1085
Frc consts -- 0.9665 0.9462 0.9462
IR Inten -- 92.8666 12.3148 12.3173
Atom AN X Y Z X Y Z X Y Z
1 5 0.00 0.00 0.16 0.00 0.10 0.00 -0.10 0.00 0.00
2 1 0.00 0.00 -0.57 0.00 0.08 0.00 0.81 0.00 0.00
3 1 0.00 0.00 -0.57 -0.38 -0.59 0.00 0.14 0.38 0.00
4 1 0.00 0.00 -0.57 0.38 -0.59 0.00 0.14 -0.38 0.00
4 5 6
A1' E' E'
Frequencies -- 2598.4264 2737.4379 2737.4386
Red. masses -- 1.0078 1.1260 1.1260
Frc consts -- 4.0092 4.9714 4.9714
IR Inten -- 0.0000 103.7400 103.7332
Now we shall move to the results which are viewed on Gassview 05. The vibrational modes and the IR spectrum of the molecule are easier to analyse on the Gassview interface since the motion of the molecule in each vibrational mode can dynamically be observed. The wavenumbers for the vibrational modes with the literature values and the dynamic motions of molecule are tabulated in the table below.
| No. | Frequency (literature value [2] for 10BH3 and 11BH3 )/ cm-1 | Intensity | Symmetry label | Mode of vibration | Dynamic motion | Description | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1144 (1137, 1125) | 93 | A2' ' | Wagging (out of plane) |
|
All three hydrogen atoms and the boron atom move out of phase; once the hydrogen atoms move up the boron atom move down and vice versa. | |||
| 2 | 1204 (1610, 1604) | 12 | E' | Scissoring (in plane) |
|
The two hydrogen atoms move inwards/outwards each other and the boron atom moves up and down. | |||
| 3 | 1204 (1610, 1604) | 12 | E' | Rocking (in plane) |
|
Two hydrogen atoms move in phase (rocking) and the other hydrogen atom moves in opposite direction to the BH2 unit with larger magnitude. | |||
| 4 | 2598 (not observed) | 0 | A1' | Symmetric stretching |
|
All hydrogen atoms move towards/outwards the boron atom. This vibration is IR-inactive as it is symmetrical. | |||
| 5 | 2737 (2826, 2808) | 104 | E' | Asymmetric stretching |
|
One hydrogen atom is fixed, the other hydrogen atoms move out of phase towards the boron atom. | |||
| 6 | 2737 (2826, 2808) | 104 | E' | Asymmetric stretching |
|
Two B-H bonds compress/expand in phase and the other B-H stretches with the larger magnitude and out of phase to the other two bonds. |
The symmetry label for each mode corresponds to the dynamic motion of the molecule. For example, for peak No. 1, A2' ' means that this vibrational mode has to be non-degenerate, symmetric to the C3 axis, but unsymmetric to the C2 axis perpendicular to the C3 axis and σh and this corresponds to the wagging mode (out of plane). In addition, the peaks with symmetry label E' have a double degeneracy, and one of the modes is a symmetrical stretch (peak No. 4), which does not cause a change in dipole (IR inacive). Consequently, instead of six peaks there are just three peaks showing on the spectrum. Finally, the calculated IR spectrum is shown below.
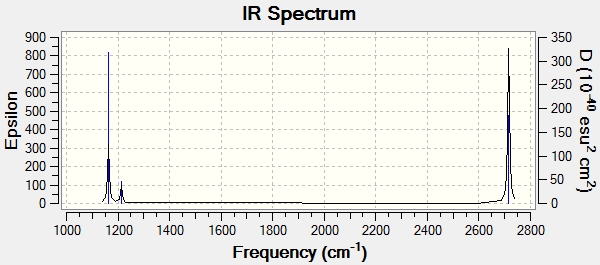
Once we move to the frequency calculation, the deviation of the calculated frequencies using 3-21G basis set from the experimental values starts to be detected. A better basis set, e.g. 6-311G, can be used to improved the results. Moreover, such a deviation may be a result from the isotropic effect as the molecule can be present as either 10BH3 or 11BH3.
Natural bond orbital (NBO) analysis
The optimised molecule was used to run the energy calculation using B3LYP method with 6-311G(d,p) basis set the additional keyword pop=(full,nbo) was added in order to activate the full natural bond orbital calculation. First of all we shall look at the charge distribution within the molecule. The result shown on the Gaussview interface (see the figure below) reveals that the boron atom has low electron density (green, 0.332) and also the high electron density is located on all three hydrogen atoms (dark red, -0.11).

Such result corresponds to the fact that BH3 is an electron deficient molecule and also a lewis acid as the boron atom has six valence electrons, which does not obey the octet rule. As a result it needs two electrons to reach an octet, eight valence electrons. In the *.log file, there is some useful information which cannot be shown in the Gaussview interface. From the *.log file, the numbers in the natural charge column (shown in boldface below) correspond to the shows on the Gaussview interface earlier. In addition, they also indicate that the molecule is neutral.
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.33621 1.99949 2.66272 0.00158 4.66379
H 2 -0.11207 0.00000 1.11052 0.00155 1.11207
H 3 -0.11207 0.00000 1.11052 0.00155 1.11207
H 4 -0.11207 0.00000 1.11052 0.00155 1.11207
=======================================================================
* Total * 0.00000 1.99949 5.99428 0.00623 8.00000
Moreover, the information from the *.log file can tell us the orbital contribution within the molecule. In this case the boron atom contributes 44.41% to the molecular orbital of BH3 meanwhile the three hydrogen atoms contribute 55.52% to the molecular orbital. The orbitals from the boron atom used to interact with the orbitals from the hydrogen atoms have 33% s-character and 67% p-character, i.e. such orbitals are sp2hybrid orbitals. For the orbitals from the hydrogen atoms, they have 100% s-character, i.e. the hydrogen atoms use s orbitals to form the bonds with sp2orbitals from the boron atom.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99720) BD ( 1) B 1 - H 2
( 44.41%) 0.6664* B 1 s( 33.32%)p 2.00( 66.62%)d 0.00( 0.06%)
0.0001 0.5772 0.0000 0.0000 0.0000
0.0000 0.0000 0.8162 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 -0.0213 -0.0122
( 55.59%) 0.7456* H 2 s( 99.93%)p 0.00( 0.07%)
0.9996 -0.0013 -0.0002 0.0000 -0.0269
0.0000
2. (1.99720) BD ( 1) B 1 - H 3
( 44.41%) 0.6664* B 1 s( 33.32%)p 2.00( 66.62%)d 0.00( 0.06%)
0.0001 0.5772 0.0000 0.0000 0.7069
0.0000 0.0000 -0.4081 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0184 0.0000
0.0000 0.0106 -0.0122
( 55.59%) 0.7456* H 3 s( 99.93%)p 0.00( 0.07%)
0.9996 -0.0013 -0.0002 -0.0233 0.0134
0.0000
3. (1.99720) BD ( 1) B 1 - H 4
( 44.41%) 0.6664* B 1 s( 33.32%)p 2.00( 66.62%)d 0.00( 0.06%)
0.0001 0.5772 0.0000 0.0000 -0.7069
0.0000 0.0000 -0.4081 0.0000 0.0000
0.0000 0.0000 0.0000 0.0184 0.0000
0.0000 0.0106 -0.0122
( 55.59%) 0.7456* H 4 s( 99.93%)p 0.00( 0.07%)
0.9996 -0.0013 -0.0002 0.0233 0.0134
0.0000
Form this information, we can conclude that the geometry of the molecule is trigonal planar as the boron atom has sp2 hybridisation and this leads to the fact that the molecule is classified in the D3h point group. If we look at the second order perturbation theory analysis, it can be seen that there is no orbital mixing taking place with the molecule as all the energies shown in the table are less than 20 kcal/mol. Therefore, all B-H bonds within the molecule are 2-centre 2-electron bonds.
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
within unit 1 1. BD ( 1) B 1 - H 2 / 35. BD*( 1) B 1 - H 3 0.54 0.80 0.019 1. BD ( 1) B 1 - H 2 / 36. BD*( 1) B 1 - H 4 0.54 0.80 0.019 2. BD ( 1) B 1 - H 3 / 34. BD*( 1) B 1 - H 2 0.54 0.80 0.019 2. BD ( 1) B 1 - H 3 / 36. BD*( 1) B 1 - H 4 0.54 0.80 0.019 3. BD ( 1) B 1 - H 4 / 34. BD*( 1) B 1 - H 2 0.54 0.80 0.019 3. BD ( 1) B 1 - H 4 / 35. BD*( 1) B 1 - H 3 0.54 0.80 0.019
Orbital analysis
In this section, the molecular orbitals (MO) 1-8 of BH3 molecule obtained from linear combination of atomic orbitals (LCAO) and density functional theory (DFT) are compared. The energy level diagram for such results are shown below.

According to the diagrams, the orders of the molecular orbitals from the LCAO method and DFT/B3YLB with 6-311G(d,p) are the same, but the result from the DFT/B3YLB with 3-21G gives the different result, the LUMO+1 and LUMO+2 swap to the other way round. The difference in the results is caused by that fact that 3-21G basis has very low accuracy. One of the drawbacks of the LCAO approach is the exact energy of each MO cannot be determined, only the relative energy can be evaluated. On the other hand the DFT method can determine the exact energy of each MO but the accuracy of the energy depends on the basis set we used and the complexity of the molecule. It is obvious to see that once the high accuracy basis set (6-311G(d,p)) is used, the results from the LCAO and DFT are corresponding to each other. That is, the shapes and symmetries from both methods are matched.

The energy levels of the MOs are confirmed by the paper from C. Tom Wickham‐Jones, Sean Moran, and G. Barney Ellison, DOI:10.1063/1.456104.
Thallium tribromide, TlBr3
Optimisation
Due to the fact that thallium tribromide, TlBr3, is much heavier than borane. As a result, the symmetry of the molecule was very tightly restricted to D3h point group, and also a pseudo potential was used in order to help the calculation go more quickly. Because there are large numbers of electrons and the relativistic effect within the molecule. In this calculation, LANL2DZ (Los Alamos National Laboratory 2 Double ζ) pseudo potential was used for the optimisation. After the optimisation, the values of forces and displacements must be converged and derivative of energy and displacement must be close to zero as follows.
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.086233D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
From the summary of the results from Gaussview, the molecule is neutral as it has zero charge; the total energy of the molecule is -91.218±0.004 Hartree; the root mean square gradient (<-DE/DX>) is 0.00; the molecule is non-polar as the dipole moment is 0.00 Debye; the molecule is in the D3h point group.

To confirm, the total energy must decrease from the starting point and The slope of the RMS Gradient Norm graph must decrease to be close or equal to zero.

The structure of the BH3 molecule after the optimisation indicates that the bond lengths for all B-H bonds are 2.65±0.01 Å (lit.[3], 2.52 Å) and all bond angles are 120°.
From this it can be concluded that for a heavy molecule such as TlBr3, LANL2DZ worked fairly accurate for the optimisation. Because the values of bond lengths obtained from the calculation are close to the literature value.
Vibrational analysis
Since the frequencies are derived from the second derivative of energy and displacement, at the minimum critical point such a derivative must be positive. Therefore, the frequencies obtained from the calculation have to be positive.
Now let us consider the data from the *.log file from the calculation, the six values at low frequencies were observed as shown below in boldface. These values come from the motions of the centre of mass of the molecule, therefore their magnitudes are much smaller than that for the molecular vibrations showing the IR spectrum shown below in underlined. Theses frequencies are close to zero.
Low frequencies --- -3.4214 -0.0026 -0.0004 0.0015 3.9366 3.9366
Low frequencies --- 46.4289 46.4292 52.1449
Diagonal vibrational polarizability:
61.4729574 61.4706377 57.8640256
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
E' E' A2"
Frequencies -- 46.4289 46.4292 52.1449
Red. masses -- 88.4613 88.4613 117.7209
Frc consts -- 0.1124 0.1124 0.1886
IR Inten -- 3.6867 3.6867 5.8466
Atom AN X Y Z X Y Z X Y Z
1 81 0.00 0.28 0.00 -0.28 0.00 0.00 0.00 0.00 0.55
2 35 0.00 0.26 0.00 0.74 0.00 0.00 0.00 0.00 -0.48
3 35 0.43 -0.49 0.00 -0.01 -0.43 0.00 0.00 0.00 -0.48
4 35 -0.43 -0.49 0.00 -0.01 0.43 0.00 0.00 0.00 -0.48
4 5 6
A1' E' E'
Frequencies -- 165.2685 210.6948 210.6949
Red. masses -- 78.9183 101.4032 101.4032
Frc consts -- 1.2700 2.6522 2.6522
IR Inten -- 0.0000 25.4830 25.4797
The wavenumbers for the vibrational modes with the literature values and the dynamic motions of molecule are summarised in the table below.
| No. | Frequency/ cm-1 | Intensity | Symmetry label | Mode of vibration | Dynamic motion | Description | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 46 | 3.7 | E' | Scissoring (in plane) |
|
The two bromine atoms move inwards/outwards each other and the thallium atom moves up and down. | |||
| 2 | 46 | 3.7 | E' | Rocking (in plane) |
|
Two bromine atoms move in phase (rocking) and the other bromine atom moves in opposite direction to the TlBr2 unit with larger magnitude. | |||
| 3 | 52 | 5,8 | A2 | Wagging (out of plane) |
|
All three bromine atoms and the thallium atom move out of phase; once the bromine atoms move up the thallium atom move down and vice versa. | |||
| 4 | 165 | 0 | A1' | Symmetric stretching |
|
All bromine atoms move towards/outwards the thallium atom. This vibration is IR-inactive as it is symmetrical. | |||
| 5 | 211 | 25.5 | E' | Asymmetric stretching |
|
One bromine atom is fixed, the other two bromine atoms move out of phase towards the thallium atom. | |||
| 6 | 211 | 25.5 | E' | Asymmetric stretching |
|
Two Tl-Br bonds compress/expand in phase and the other Ti-Br stretches with the larger magnitude and out of phase to the other two bonds. |
The symmetry label for each mode corresponds to the dynamic motion of the molecule. For example, for peak No. 1, peak No. 2 and peak No. 5, peak No. 6, E' means that these vibrational modes have to be double-degenerate, and these correspond to scissoring and rocking modes (in plane). In addition, the peak No.3 with symmetry label A2 has a non-degeneracy and Peaks No.1 2 and 3 are close to each other hence show one broad peak. One of the modes is a symmetrical stretch (peak No. 4), which does not cause a change in dipole (IR inacive). Consequently, instead of six peaks there are just 2 peaks showing on the spectrum below.
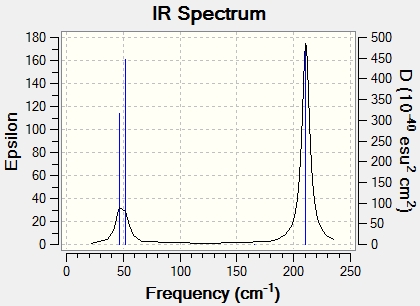
Cis-, trans- isomerisation of MO(CO)4(PCl3)2
Optimisation
DOI:10042/to-11099 DOI:10042/to-11102
Both cis- and trans- isomers of MO(CO)4(PCl3)2 were optimised using DFT/B3LYP with LANL2MB (minimal basis set) and also the additional keyword opt=loose. The general information obtained from the optimisation is shown as follows.
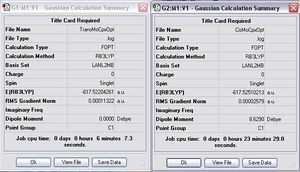
Item Value Threshold Converged? Maximum Force 0.000104 0.002500 YES RMS Force 0.000018 0.001667 YES Maximum Displacement 0.003201 0.010000 YES RMS Displacement 0.000725 0.006667 YES
Item Value Threshold Converged? Maximum Force 0.000415 0.002500 YES RMS Force 0.000155 0.001667 YES Maximum Displacement 0.006123 0.010000 YES RMS Displacement 0.002081 0.006667 YES
From the information above, the values of RMS Gradient Norm for both complexes are close to zero as well as the forces and displacements are converged. This implies that the optimisation was completed. In order to increase the accuracy of the data, the second optimisation was done with a better basis set, LANL2DZ. In addition, the geometries of the complexes were configured to better positions with the additional keyword int=ultrafine scf=conver=9. The general information from the second optimisation is summarised as follows.
DOI:10042/to-11100 DOI:10042/to-11103
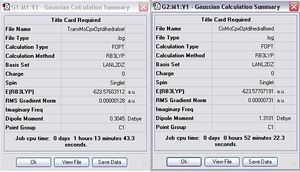
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.002300 0.001800 YES RMS Displacement 0.000551 0.001200 YES
Item Value Threshold Converged? Maximum Force 0.000021 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.001634 0.001800 YES RMS Displacement 0.000530 0.001200 YES
From these we know that the second optimisations for both complexes were successfully done.
According to the summary windows, the trans-isomer has slightly lower energy than the cis-isomer. However, the energy difference (0.001 Hartee) is smaller than the error in energy calculated by Gaussian (±0.004 Hartee). Therefore, it cannot be concluded that the trans-isomer is more stable than the cis-isomer.
From the second optimisation, the values of bond lengths and the literature values for both cis- and trans- complexes are tabulated in the following tables.
| Bonds | Bond lengths from Gaussian/ Å | literature values [4]/ Å |
|---|---|---|
| Mo-C | 2.06 | 2.01 |
| Mo-P | 2.44 | 2.50 |
| C=O | 1.17 | 1.17 |
| P-Cl | 2.24 | N/A |
| Bonds | Bond lengths from Gaussian/ Å | literature values [5]/ Å |
|---|---|---|
| Mo-C (axial) | 2.06 | 2.02 |
| Mo-C (equatorial) | 2.01 | 1.97 |
| Mo-P | 2.51 | 2.56 |
| C=O (axial) | 1.17 | 1.16 |
| C=O (equatorial) | 1.18 | 1.16 |
| P-Cl | 2.24 | N/A |
The literature values are from Mo(CO)4(PPh3)2 molecule not Mo(CO)4(PCl3)2 molecule, because the triphenylphosphine ligands are very bulky ligands and can slow down the calculations. As a result in this study the phosphorus trichloride ligands were used instead of the triphenylphosphine ligands. Even though, the complexes are different, the calculations provide very accurate bond lengths within the complexes.
The reason for that all P-Cl bonds are not shown in Gaussview interface is all phosphorus atoms within the molybdenum complexes are hyper-valence atoms and Gaussian did not take d-orbital in the phosphorus atom into the calculation.
In order to solve this problem the extra basis was added into the calculation by adding some extra code (shown below) into the input file.
(blank line) P 0 D 1 1.0 0.55 0.100D+01 **** (blank line)
DOI:10042/to-11101 DOI:10042/to-11104
Now the d-orbital in the phosphorus atoms will be taken into account, then the P-Cl bonds in the complexes are shown.
The optimisations after the extra basis has been added shown that the structures of both complexes have reached the minimum energy point.


Item Value Threshold Converged? Maximum Force 0.000043 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.000556 0.001800 YES RMS Displacement 0.000140 0.001200 YES Predicted change in Energy=-2.212995D-08 Optimization completed. -- Stationary point found.
Item Value Threshold Converged? Maximum Force 0.000142 0.000450 YES RMS Force 0.000045 0.000300 YES Maximum Displacement 0.001275 0.001800 YES RMS Displacement 0.000467 0.001200 YES Predicted change in Energy=-2.521169D-07 Optimization completed. -- Stationary point found.
To ensure that both structures have reached the minimum critical points not maximum the frequency calculations were carried out in the next section.
Vibrational analysis
DOI:10042/to-11105 DOI:10042/to-11106
The frequencies obtained from the calculations are all positive. Therefore, the optimisations in the previous section were successfully done, the structures are at the minimum energy potential.
For both isomers we will focus on just the CO stretches (2100-1700 cm-1) as both complexes will provide different types of such stretches .
The vibrational modes and frequencies of both isomers are tabulated and summarised in the following tables.
| Frequencies (literature values[6]/cm-1 | symmetry lable | Descriptions |
|---|---|---|
| 1950 (1896) | A | Asymmetric C=O stretches |
| 1951 (1896) | A | Asymmetric C=O stretches |
| Frequencies (literature values [7]/cm-1 | symmetry lable | Descriptions |
|---|---|---|
| 1806 (1946) | A | Asymmetric C=O stretches |
| 1807 (1949) | A | Asymmetric C=O stretches |
| 1817 (1959) | A | Asymmetric C=O stretches |
| 1873 (2024) | A | Symmetric C=O stretches |
As expected, thr trans-isomer gives less mode of CO stretches than the cis-isomer, because the trans-isomer has higher symmetry than the cis-isomer.
Mini Project: The methylation on an ethylimidazole[8]

Optimisations
DOI:10042/to-11107 DOI:10042/to-11108 DOI:10042/to-11109 DOI:10042/to-11110
The structure of ethylimidazole 1a was optimised using DFT/B3YLP with 3-21G basis set at the beginning in order to obtain a rough optimised structure of it. The optimisation was done successfully as the forces and displacements are converged as well as the total energy decreased from the the starting point and the gradient in RMS Gradient Norm approached zero as the optimisation going. Such results are shown as follows.
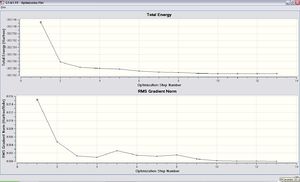
Item Value Threshold Converged? Maximum Force 0.000014 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000453 0.001800 YES RMS Displacement 0.000147 0.001200 YES Predicted change in Energy=-3.316387D-09 Optimization completed. -- Stationary point found.
The molecule from the first optimisation was used to carry on the second optimisation (DFT/B3YLP with 6-311G basis set) to yield the fine structure of 1a.The second optimisation was confirmed to be completed as follows.
DOI:10042/to-11111 DOI:10042/to-11112 DOI:10042/to-11113 DOI:10042/to-11114

Item Value Threshold Converged? Maximum Force 0.000022 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000608 0.001800 YES RMS Displacement 0.000152 0.001200 YES Predicted change in Energy=-6.505691D-09 Optimization completed. -- Stationary point found.
The structures for compound 2a, 3a and 4a were done in the same was as 1a. Their results are shown as follows.
For 2a:

Item Value Threshold Converged? Maximum Force 0.000219 0.000450 YES RMS Force 0.000060 0.000300 YES Maximum Displacement 0.001400 0.001800 YES RMS Displacement 0.000516 0.001200 YES Predicted change in Energy=-3.299091D-07 Optimization completed. -- Stationary point found.

Item Value Threshold Converged? Maximum Force 0.000044 0.000450 YES RMS Force 0.000014 0.000300 YES Maximum Displacement 0.000342 0.001800 YES RMS Displacement 0.000116 0.001200 YES Predicted change in Energy=-1.567034D-08 Optimization completed. -- Stationary point found.
For 3a:

Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.000842 0.001800 YES RMS Displacement 0.000234 0.001200 YES Predicted change in Energy=-1.062290D-09 Optimization completed. -- Stationary point found.

Item Value Threshold Converged? Maximum Force 0.000168 0.000450 YES RMS Force 0.000032 0.000300 YES Maximum Displacement 0.001774 0.001800 YES RMS Displacement 0.000463 0.001200 YES Predicted change in Energy=-1.579196D-07 Optimization completed. -- Stationary point found.
For 4a:

Item Value Threshold Converged? Maximum Force 0.000439 0.000450 YES RMS Force 0.000125 0.000300 YES Maximum Displacement 0.001586 0.001800 YES RMS Displacement 0.000635 0.001200 YES Predicted change in Energy=-7.611706D-07 Optimization completed. -- Stationary point found.

Item Value Threshold Converged? Maximum Force 0.000043 0.000450 YES RMS Force 0.000021 0.000300 YES Maximum Displacement 0.000290 0.001800 YES RMS Displacement 0.000090 0.001200 YES Predicted change in Energy=-1.444968D-08 Optimization completed. -- Stationary point found.
The bond lengths within 1a, 2a, 3a and 4a are summarised in the following table.
| Bonds | Bond lengths within 1a/ Å | Bond lengths within 3a/ Å |
|---|---|---|
| CH at 1 | 1.09 | 1.09 |
| CH at 2 | 1.09 | 1.09 |
| CH at 4 | 1.08 | 1.08 |
| CH at 5 | 1.08 | 1.08 |
| CH at 7 | 1.08 | 1.08 |
| CC (1,2) | 1.53 | 1.52 |
| CN (2,3) (3,4) (5,6) (7,3) | 1.46 1.38 1.37 1.37 | 1.49 1.38 1.38 1.34 |
| C=C (4,5) | 1.37 | 1.36 |
| C=N (6,7) | 1.31 | 1.34 |
| CN at 6 | N/A | 1.47 |
| CH on methyl at 6 | N/A | 1.09 |

The CN bonds at (3,4) (5,6) and (7,3) are shorter than the CN bonds at (2,3) but are close to the C=N at (6,7) because of the resonance effect within the imidazole ring.
| Bonds | Bond lengths within 2a/ Å | Bond lengths within 4a/ Å |
|---|---|---|
| CF | 1.33 | 1.35 |
| CS | 1.88 | 1.88 |
| S=O | 1.45 | 1.47 |
| SO | 1.62 | N/A |
| CO | 1.46 | N/A |
| CH | 1.09 | N/A |
For 4a, the S-O bond length is not observed because of the resonance effect. In addition S=O bonds within the 2a are slightly shorter than the ones within 4a as there is less effect of bond resonance within 2a than 4a because one of the oxygen atom in 2a bonded with methyl.
Frequency analysis
DOI:10042/to-11115 DOI:10042/to-11116 DOI:10042/to-11117 DOI:10042/to-11118
The optimised structures for 1a, 2a, 3a and 4a were used for the frequency calculation using DFT/B3LYP with 6-311G basis set.
The results for each species are shown as following.
For 1a: all frequencies showing on the IR spectrum have positive values. That is, the optimised structure of 1a is at the minimum energy. The significant vibrational modes for 1a are shown in the following table.
| Frequencies/cm-1 | symmetry lable | Descriptions |
|---|---|---|
| 919.13 | A | N(6)C2 in the ring, symmetric stretches |
| 1047 | A | N(3)C2 in the ring, symmetric stretches |
| 1141 | A | CN (5,6) in the ring, stretches |
| 1413 and 1418 | A | N(6)C2 in the ring, asymmetric stretches |
| 1530 | A | C=C and C=N in the ring, symmetric stretches |
| 1141 | A | C=C and C=N in the ring, asymmetric stretches |
| over 3000 | A | CH stretches |
For 3a: all frequencies showing on the IR spectrum have positive values. That is, the optimised structure of 3a is at the minimum energy. The significant vibrational modes for 3a are shown in the following table.
| Frequencies/cm-1 | symmetry lable | Descriptions |
|---|---|---|
| 1037 | A | N(6)C2 in the ring, symmetric stretches |
| 1049 | A | N(3)C2 in the ring, symmetric stretches |
| 1410 | A | N(6)C2 in the ring, asymmetric stretches |
| 1602 | A | C=N in the ring, stretches |
| 1609 | A | C=C in the ring, stretches |
| over 3000 | A | CH stretches |
We can see from the tables above that the in-ring stretching modes of 3a have lower frequencies than that for 1a. This might be due to the fact that the nitrogen atom at position 6 within 3aare bonded more rigidly to the surrounding atoms compared that for 1a. Moreover, C=C and C=N stretches within 3a have different frequencies while the ones within 1a have the same frequency. This takes place with the same reason as the former case, the imidazole ring of 3a is more rigid than that in 1a.
Now move to the frequency comparison between 2a and 4a.
The important bond vibrations within 2a and 4a are shown in the following tables.
| Frequencies/cm-1 | symmetry lable | Descriptions |
|---|---|---|
| 719 | A | C-S-O symmetric stretches |
| 777 | A | C-S-O asymmetric stretches |
| 989 | A | C-O symmetric stretches |
| 1100 | A | S=O symmetry stretches |
| 1228 | A | CF stretches |
| 1354 | A | S=O asymmetric stretches |
| over 3000 | A | CH stretches |
| Frequencies/cm-1 | symmetry lable | Descriptions |
|---|---|---|
| 989 | A | S=O symmetric stretches |
| 1137 | A | CF stretches |
| 1197 | A | C-S stretches |
| 1237 | A | S=O asymmetric stretches |
For 4a, the S-O stretches are not observed because the all SO bonds are equivalent due to the resonance. In addition, the SO stretches in 4a have higher frequency than that in 2a because there is not methyl group within 4a.
Orbital analysis for ethylimidazole, 1a
The significant molecular orbitals are shown in this section with the descriptions.







The molecular orbitals 1-7 are 1S orbitals of the nitrogen atoms and carbon atoms, which are too deep down in energy to interact with other orbitals from other atoms.

The molecular orbital 8 is the overlap between 2S orbitals of the nitrogen atoms and the carbon atoms.


The molecular orbitals 21 22 show the delocalisation of electrons within the imidazole ring.


The molecular orbitals 24 26 illustrate the shape of HOMOs where are located on the alkenes on the imidazole ring. Moreover, this is corresponding to the chemistry knowledge that the alkenes on an imidazole ring are very reactive to the electrophiles.

The molecular orbital indicates the big lobe on the nitrogen atom at position 6, which corresponds to the lone pair of the nitrogen atom. In the methylation of ethylimidazole. the imidazole uses this lobe to interact with the LUMO of the methylating reagent e.g. CF3SO3Me to methylate the imidazole ring.

The molecular orbitals 25 illustrates the LUMO. The shape of the LUMO indicates the fact that the carbon atoms at position 4 and 7 are electrophilic centres.
Reaction energy
From the optimisations, it can be seen that the energies for 1a and 2a are shown as follows. The energy for the reactants is equal to -304.9236 Hartees + -1001.5089 Hartees = -1306.4325 Hartees.

Likewise, for the products, the energies for 3a and 4a are shown as follows and the energy for the products is equal to -344.6348 Hartees + -961.7017 Hartees = -1306.4319 Hartees.

According to this information, the energy of the reactants is slightly lower that that for the product. Therefore the energy difference between these two stagesis equal 0.0006 Hartee or 1.58 kJ/mol. Once again the difference is smaller than the magnitude of the errors from the calculations of Gaussian (about 0.004 Hartee or about 10 kJ/mol). Consequently, it cannot be concluded that whether the reaction is exothermic or endothermic. That is, we cannot say that the reaction is thermodynamically favoured or not.
Further study
The study in kinetics point of view, for example, the stability (energy) of the transition state should be done in order to judge how fast the reaction can undergo. Moreover, the actual Gibb's free energy for each species should be determined rather than the energy as once the free energies are known the Gibb's free energy of the reaction and the equilibrium constant of the reaction can be calculated. Therefore, we can know exactly whether the reaction is thermodynamically favourable or not.
References
- ↑ 1.0 1.1 DOI:10.1021/ja00505a009
- ↑ DOI:10.1021/ja00738a008
- ↑ DOI:10.1021/ja00123a011
- ↑ G. Hogarth, T. Norman, Inorganica Chemica Acta 254 (1997) 167- 171.
- ↑ F.A. Cotton, D.J. Darensbourg, S. Klein and B.W.S. Kolthammer. Inorg. Chem. 21 (1982), p. 294.
- ↑ ELmer C. Alyea and Shuquan Song, Inorg. Chem., 1995, 34, 3864-3873
- ↑ ELmer C. Alyea and Shuquan Song, Inorg. Chem., 1995, 34, 3864-3873
- ↑ Housecroft C.E and Sharpe A.G. Inorganic Chemistry, 2nd edn, p.229.
