Rep:Mod:AM7412
Computational Studies of Transition Structures for Pericyclic Reactions
Introduction
This study involves identifying the transition state structures for well recognised pericylic reactions using several computational methods that use molecular orbital based methods to numerically solve the Schrodinger equation by mapping put the potential energy surface for the reaction pathway. These potential energy surfaces can be used to extract vital information including vibrational modes of the species and energies, including the activation energy for the reaction which can be obtained by analysing crucial thermochemistry data. Understanding the structure of the transition state, a structure which lies at a maximum saddle point on the potential energy surface of the reaction under investigation can provide us with a fundamental understanding of the kinetics, regioselectivity and reaction mechanisms of that reaction.
A Cope Rearrangement and a Diels-Alder reaction stem from a fundamental part of Chemistry referred to as pericyclic reactions. Pericyclic reactions are reactions which occur in a concerted fashion, normally involving π clouds and proceed through a cyclic transition state. The two sub-groups of pericyclic reactions in which a Cope Rearrangement and a Diels-Alder reaction stem from are referred to as [3,3] sigmatropic reactions and cycloadditions respectively.
All energies quoted throughout this study are in Hartree au units, whereby 1 Hartree au = 627.509 kcal/mol, unless otherwise stated.
The Cope Rearrangement
A sigmatropic reaction involves the net conversion of one σ-bond into another, through a rearrangement of the π-system (1). Sigmatropic reactions can occur in two fashions, the first being in a suprafacial manner and the second in an antarafacial manner. For a [3,3]-shift however this is not an issue as the 6-electron (4n+2, where n is the number of π-electrons) process is symmetrical and thus undergoes a suprafacial, Huckel topology transition state under thermal conditions as predicted by the Woodward-Hoffman rules (2). The Cope rearrangement, although is a pericyclic reaction, the transition state can be argued to resemble that of a diradical, both structurally and energetically. The reason for the di-radical like structure is a result of preserving orbital symmetry. This concept is a plausible explanation as to why Cope rearrangements are generally high energy processes. Theoretically however the reaction is believed to proceed via a homoaromatic transition state, with a lower reaction energy pathway (3).
In this computational study of the Cope rearrangement, the structure of the transition states for rearrangement 1,5-hexadiene as well as the minima of the potential energy surface were identified and used to determine the favoured reaction pathway. The mechanism can either proceed through a chair or a boat transition state, with the boat conformation of the transition state theoretically being higher in energy and thus disfavoured. Prior to identifying which transition state structure is preferred, GaussView was used to construct and optimise (using Hartree-Fock and DFT level theory) the conformers of 1,5-hexadiene to locate which conformer is most stable - only anti-periplanar and gauche conformations were investigated.
Optimising the Reactants and Products
Optimisation of Anti-periplanar and Gauche Conformers of 1,5-hexadiene
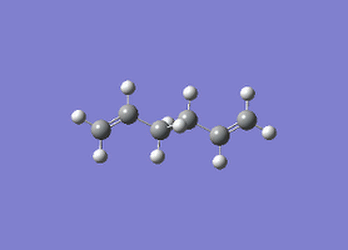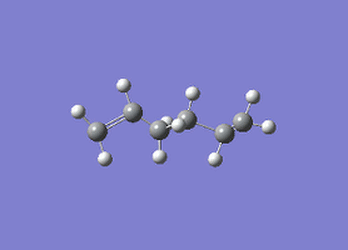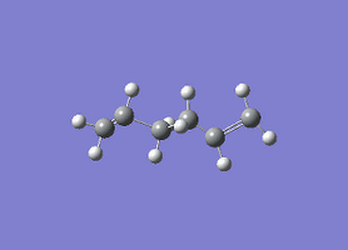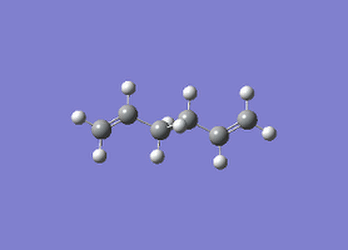
The anti-periplanar conformation of 1,5-hexadiene was constructed using a cyclohexane chair conformer as a starting point and adding the necessary double bonds in the 1 and 5 positions ring as well as deleting the C-C bond at the 1,6 position on the chair. Subsequently, to obtain an anti-periplanar conformation the dihedral angle of each of the four terminal carbon atoms, as well as the central four carbon atoms were altered to 180°. This conformation was then cleaned and optimised using Hartree-Fock theory with a 3-21G basis set to minimise its energy (see Table 1 for energies and point group)
|
Following the generation of the anti-periplanar conformation of 1,5-hexadiene a gauche conformation was constructed by altering the dihedral angle of the central four carbon atoms to 60° rather than 180°. This conformation was then optimised using the same theory and basis set as above to yield a conformer with an energy of -231.69153032 and a C2 point group, once symmetrised.
|
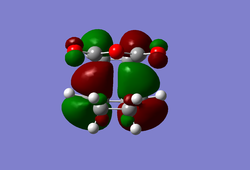
Theoretically there are 27 conformations for 1,5-hexadiene however only 10 of these 27 are chemically distinct and thus have a different total energy. 17 of the conformations are not unique to the presence of enantiomers, making several conformers identical. From the computed energies of the two conformations in Table 1 it can be seen that the energy of the anti-periplanar structure is slightly lower than the gauche4 conformation. This is line with theoretical findings as a result of reduced steric interaction between the vinyl side groups. However, referring to Table 1, from computing the "gauche3" conformer it can be seen that this conformer has the lowest energy and is thus the most stable conformer of 1,5-hexadiene. The reasoning behind this is a result of hyperconjugation, whereby there is a significant overlap between the two π-orbitals of the two C=C double bonds (see figure below). The favourable interaction lowers energy of the respective bonding orbitals, stabilising the gauche3 conformer. These π-π interactions are seen in other conformers such as the gauche4, however maximal overlap is observed in the gauche3 conformer leading to maximal stabilisation as a result of delocalisation of charge within the molecule. The absence of interaction of bonding orbitals in the anti-periplanar conformer makes it slightly higher in energy than the gauche conformer, which is known as the "gauche effect" - energy of a gauche conformer is lower in energy than an anti-periplanar one. One can argue that the difference in energy between the gauche3 and anti2 conformer is extremely small such that by using different computational optimisation techniques the energies of the conformers could vary such that anti2 is more stable than gauche3.  As the structure of the Ci anti2 conformer was previously located it was further optimised using the DFT theory and a 6-31G* (larger) basis set - the energy was found to be -234.62683050 with retention in the point group. This suggests that the change in overall geometry between the two conformations is minimal due to the preservation of the Ci point group (Note that you could have the same symmetry point group but still have very different structures. João (talk) 14:29, 28 December 2014 (UTC)). Minor perturbations were apparent when the bond angles and bond lengths of the two conformers from different levels of theory were analysed (see Table 2).
Although the bond angles and lengths have not changed significantly there is a considerable difference in energies computed from the two basis sets of 2.93429521 Hartree units (1841.3 kcal/mol). This shows that by using a larger, more accurate basis set the energy of the conformation can vary drastically with minimal observable change in geometry. Frequency Analysis of Anti2 ConformerA frequency calculation was run on the B3LYP/6-31G* optimised anti2 conformer to enable us to compare with experimentally measured values as the energies found above simply represent the energy of the conformer on a bare potential energy surface. The resulting vibrational modes were all found to be positive and real, implying that the conformer resides at a critical point on the potential energy surface and is thus a true local minimum. From the 42 vibrational frequencies obtained it was noted that not all of them were IR active as there was no net change in dipole moment (see Figure 5). The peaks at 1727.28 cm-1 and 1730.56 cm-1 were identified to be the symmetric and asymmetric stretches of the two C=C double bonds respectively and are presented below. These are the vibrational modes of the molecule which are of interest as they correspond to the motion of the C=C double bond which is involved in the Cope rearrangement. Other characteristic peaks for 1,5-hexadiene in the IR spectrum are the sp3 C-H stretches found in the region of 2850-3200 cm-1. 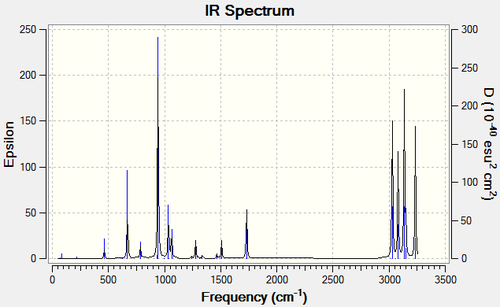 Figure 5: IR Spectrum of Anti2 Conformer at 298.15 K
Through conducting frequency analysis on the 1,5-hexadiene conformer vital thermochemistry data was obtained at 298.15 K.
The first of these values (sum of electronic and zero-point vibrational energies, E = Eelec + ZPE) corresponds to the energy of the molecule at 0 K. The second of these values (sum of electronic and thermal energies) corresponds to the energy of the molecules at 298.15 K and 1 atm which takes into account all of the rotational, vibrational and translational energy modes present (E = Eelec + Erot + Evib + Etrans). The thirs value (sum of electronic and thermal enthalpies) corresponds to the enthalpy of the molecule which takes into account an additional RT term, where R is the gas constant and T is temperature in Kelvin. This value becomes of great importance in dissociation reactions (Why? What does this RT term correspond to? João (talk) 14:29, 28 December 2014 (UTC)) and is thus not essential when looking at [3,3] sigmatropic reactions which lack the dissociation of molecules. The final value (sum of electronic and thermal free energies) incorporates the entropic contribution to the free energy (4) (How could the entropy be evaluated in this case? João (talk) 14:29, 28 December 2014 (UTC)). To observe the effect of temperature on the thermochemistry of a molecule subsequent studies were undertaken at 0.01 K. This temperature was used as it would provide chemical information about the molecule which would resemble that of 0 K, but at the same time it is a temperature that can be experimentally achieved under laboratory conditions (How do you obtain 0K conditions in the laboratory? 0K values can perhaps be obtained by extrapolation. João (talk) 14:29, 28 December 2014 (UTC)). The results obtained from this study are provided below.
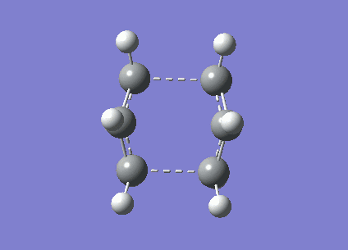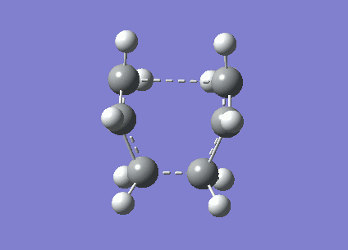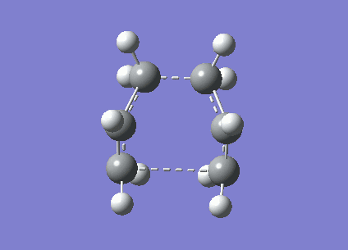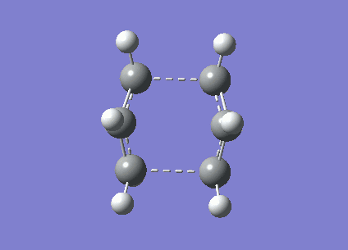
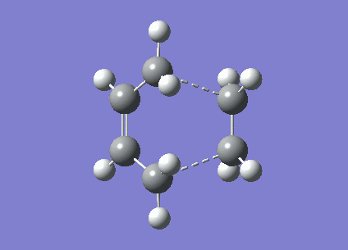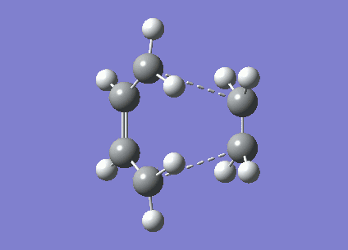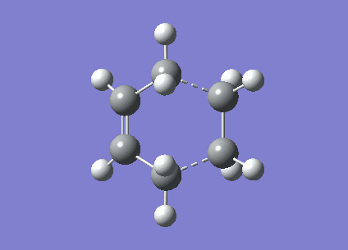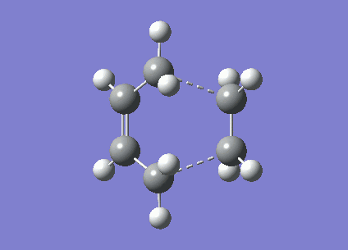
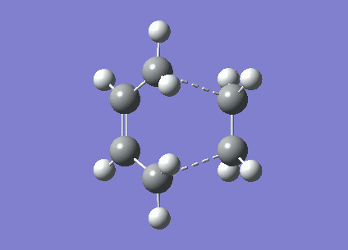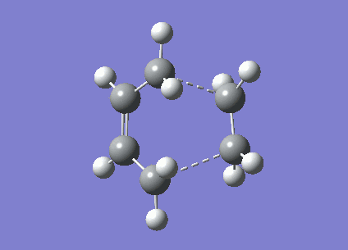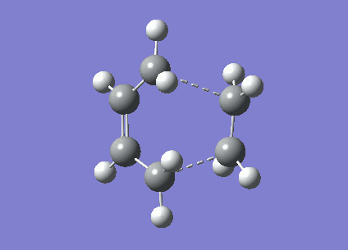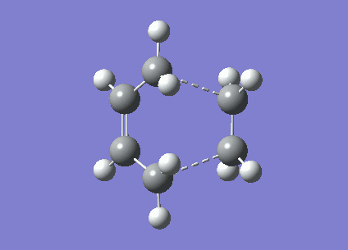
It can be seen from Table 4 that all of the values are equal which is expected as the molecule is residing in its ground state - the energy of the molecule is equal to the electronic energy as there is "no" zero-point vibrational energy (How can there be no zero-point energy? Is the Heisenberg principle violated? Is the value reported in the table the same you reported for the electronic energy above? João (talk) 14:29, 28 December 2014 (UTC)), no rotational, vibrational or translational energy, RT ~ 0 and the entropic term of the Gibbs Free Energy equation ~ 0. Comparing the values from Table 3 and Table 4, everything besides the electronic + zero-point energy decreases on going to a lower temperature. This can further be explained by the fact that in the ground state of any species there is a no heat capacity and as a result the electrons in the molecule cannot get excited to a different energy level forcing both entropy and enthalpy to decrease. Optimising 'Chair' and 'Boat' Transition StructuresIt is known that the transition state for the Cope rearrangement can resemble either a 'chair' or a 'boat' structure, both leading to a different reaction pathway. These structures will be optimised in this study through three different optimisation methods. The energies of the two possible transition states will then be compared to identify which transition structure the reaction is likely to proceed through. Identifying and Optimising an Allyl FragmentAn allyl (C3H5) was initially drawn and optimised to a minimum using the HF/3-21G method to yield the structure presented below. The optimised structure was comparable to half of the chair transition structure that is predicted.  Figure 6: Optimised Allyl Fragment Optimisation of the Chair Transition StateThe optimised structure was then duplicated and re-positioned to construct the 'guess' chair transition state. This was achieved by modifying the separation of both the terminal carbon atoms of each allyl fragment to 2.2 Å. The resulting structure was symmetrised yielding a C2v point group, indicative of the chair transition state. The guess transition state structure was then optimised using the TS Berny setting of the Hartree-Fock method with a 3-21G basis set. In this instance a new keyword ("Opt=NoEigen") was added to the computation to prevent the calculation from crashing if more than one imaginary frequency is present. The optimised transition structure had an energy of -231.61932216 with the C-C separations between the allyl fragments optimised to 2.02134 Å (C1-C1), 2.87982 Å (C2-C2) and 2.02162 Å (C3-C3) _final.png) Figure 7: Hartree-Fock Optimised Chair Transition State
Frequency analysis of the optimised chair transition state above yielded an imaginary frequency at -817.92 cm-1, confirming the formation of a transition state. The simulation of this imaginary frequency agrees with the predicted motion expected from the two allyl fragments coming together in the chair transition state of the Cope rearrangement.
Figure 8: Vibrational Mode of the Chair Transition State Optimisation using the Frozen Coordinate MethodThe chair transition state had also be been located using a frozen coordinate method. In this computational technique the two allyl fragments were once again arranged in a chair transition structure as in the method above and the resulting structure was symmetrised. However, in this case the two terminal carbon atoms of the allyl fragments were frozen to 2.2 Å and the structure optimised to a minimum. After the first optimisation was successful a subsequent optimisation was undertaken using a TS Berny setting with the HF/3-21G method on the previously frozen terminal carbon atoms of the allyl fragments by changing them to unfrozen and to a derivative. As done in previous calculations the Opt=NoEigen keyword was inserted into the computation but in this instance no force constants were computed (Force constants are actually computed numerically but only for the bonds forming/breaking, instead of make the computation for the full molecule. Some information about the surface curvature is needed in order to compute the transition state. João (talk) 14:29, 28 December 2014 (UTC)). The resulting transition state resembled closely that obtained from the simple HF/3-21G method above. The optimised transition structure had an energy of -231.61932227 with C-C separations between the allyl fragments of 2.02062 Å (C1-C1), 2.87884 Å (C2-C2) and 2.02052 Å (C3-C3). The generation of the transition state was confirmed by analysis of the RMS gradient - converged towards 0 (maxima on potential energy surface has been located). (A geometry where the gradient has reached zero is indeed a critical point. But how do you confirm it is a transition state? Did you check for imaginary frequencies? João (talk) 14:29, 28 December 2014 (UTC))
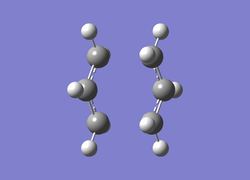.png) As both computational methods gave the same conformer for the chair transition state one can conclude that the two techniques are reliable in predicting both geometry and the energy of the molecule as only a very small discrepancy was observed between the two models. Optimisation of the Boat Transition StateQST2 MethodThe QST2 method can be used to isolate the transition state by interpolating between the reactant and product of the reaction. In order for this calculation to occur successfully all of the atoms in both the reactant and product need to be labelled correctly such that the correlate with the pathway of the reaction. The first calculation was performed on the optimised anti2 1,5-hexadiene conformer using TS (QST2) with the Hartree-Fock method (HF/3-21G). The calculation produced a structure which did not correspond to the boat transition state along with an incorrect vibrational mode. (Why is the vibrational mode incorrect? Isn't it the same vibrational mode you obtained for the chair structure? João (talk) 14:29, 28 December 2014 (UTC))
The inability of Gaussian to compute the correct boat transition structure is a result of the programme being unable to rotate the allyl fragments. Instead it has simply translated the two fragments with respect to each other leading a distorted chair conformation as can be seen by the dashed lines in the structure above. To try and identify the boat transition structure the dihedral angles in both the reactant (anti2 1,5-hexadiene conformer) and the product were altered to 0° for the central four carbon atoms and 100° for carbon atoms C2-C4 and C3-C5 to resemble the boat transition state. Once these modifications had been implemented the the calculation was re-run on this structure and it successfully yielded a boat transition state with an imaginary vibration at -839.98 cm-1.
Although both the chair and boat transition states were identified using the computations used above, it is hard to tell, almost impossible which conformer of 1,5-hexadiene they will lead to during the course of a reaction. This can be determined by undertaking another technique (see below). Intrinsic Reaction Coordinate MethodThe intrinsic reaction coordinate (IRC) method allows one to follow the minimum energy pathway from a transition state structure to a local minimum on the potential energy surface by introducing minute changes in the atomic coordinates of the structure and following the energy of the resulting structures. As the reaction being considered is symmetrical, the reaction coordinate was computed in one direction (forward). The IRC computation was run using both 50 steps and 100 steps to confirm the location of the chair transition state but also the product formed. It was found that in both cases the chair transition state structure was identified in 44 steps, the structure of which is shown below and led to the correct product, of which the energy is -231.69157817. 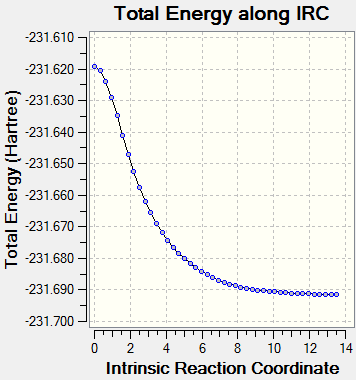IRC_profile.png)
IRC2.gif) To obtain an improved model of the product obtained from the chair transition state, the structure obtained from the IRC calculation with 50 steps was optimised to a minimum using a Hartree-Fock (HF/3-21G) method with a TS Berny setting. This yielded a molecule with a C2 point group and an energy of -231.69166702, proving the optimisation was successful as the energy is lower than that which was previously obtained but also the RMS gradient had converged to 0 (0.00000476), implying the confirmation that the product lies on a plateau whereby the gradient is ~ 0.
From running this IRC method it can be concluded that the predicted 'chair' transition state will lead to the formation of the gauche2 conformer, due to the similarity of the energy and point group obtained from the IRC calculation as well as previous methods (see Table 1). Optimisation using a Higher Basis SetThe previously optimised chair and boat transition state structures were further optimised using a larger basis set with DFT theory (B3LYP/6-31G*) giving a chair transition state structure with an energy of -234.57196486 and a point group of C2h, whereas that for the boat transition structure was -234.55864231 with a C2v point group. From these newly optimised transition states (structures shown previously (Were there any changes in the geometries? João (talk) 14:29, 28 December 2014 (UTC))) frequency analysis showed an imaginary vibration at -571.76 cm-1 and -521.96 cm-1 for the chair and boat transition states respectively. Both of these imaginary frequencies confirm that the transition state has been located and correspond to the correct vibrational mode.
From the frequency analysis of the two transition states it was also possible to extract thermochemistry data to calculate the activation energy governing the reaction for each of the transition states. This is simply done by subtracting the energy of the reactants from the energy of the transition state either at 0 K or at 298.15 K.
Summary of energies (in hartree au)
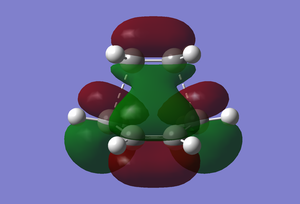
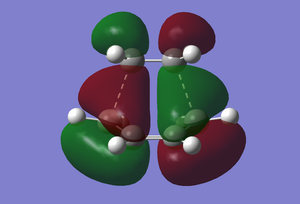
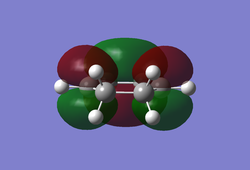
These value agree well with those listed in 'appendix 2' highlighting the fact that the computational methods used are reliable in producing valid data. Moreover, it can be seen that the energy of the chair transition state is significantly lower than the boat transition state in both computational methods implying that the reaction pathway that is favoured is one that proceeds through the chair transition state, which is expected due to the chair conformation being lower in energy. Diels Alder CycloadditionA Diels Alder reaction is a cycloaddition reaction in which two or more unsaturated molecules combine producing a cyclic product in which there is a net reduction in the number of bonds (Is there a net reduction of the number of bonds in your case? Aren't 2 bonds being formed? João (talk) 14:29, 28 December 2014 (UTC)) (International Union of Pure and Applied Chemistry (IUPAC)). Although it is entropically disfavoured as you are going from 2 reactants to one product, the process is however thermodynamically favoured as you are forming two new sigma bonds. The Diels Alder reaction is a [4+2] cycloadditon process involving a diene and a dienophile that is allowed to proceed thermally in a suprafacial/suprafacial manner. The reaction proceeds through a concerted mechanism, thus eliminating any possibility of any intermediates but instead enforces extreme selectivity on the orbital symmetry considerations of the transition state (1). A Diels-Alder reaction can proceed by a normal demand route or an inverse demand route. In the former, the diene’s HOMO (π-orbital) interacts with the LUMO (π*-orbital) of the dienophile if the diene contains and electron-donating group and the dienophile contains an electron-withdrawing group. If the location of the electron-donating/withdrawing groups are reversed the reaction occurs through the latter case (inverse demand). Similar to the [3,3]-sigmatropic reaction where the mechanism is thought to proceed in a concerted manner, a biradical intermediate has been proposed (5). In order for a Diels-Alder reaction to occur successfully the two components need to be in the correct orientation – the diene needs to exist in the s-cis conformation as there is better orbital overlap between the diene and the dienophile in this instance. In the case of butadiene however, its preferred conformation is s-trans which results in poor Diels-Alder reaction efficiency. The reason why the reaction can proceed is due to the low barrier to rotation between the s-cis and s-trans conformer (1). Diels Alder reaction between Cis-Butadiene and EtheneThe constituent fragments for this reaction, cis-butadiene and ethene were both constructed using Gaussview and independently optimised to a minimum using the AM1 semi-empirical method. The molecular orbitals of each of these reactants were computed showing that the HOMO of cis-butadiene is anti-symmetric with respect to the plane of symmetry and the LUMO is symmetric. However, for ethene the opposite is found whereby the HOMO is symmetric and the LUMO is anti-symmetric. These molecular orbitals have been derived theoretically from the linear combination of atomic orbitals (LCAO) from the individual fragments.
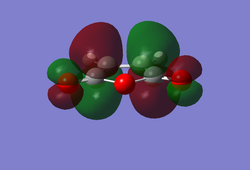
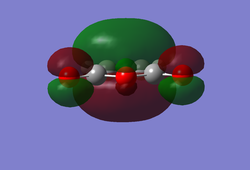
Post-optimisation the cis-butadiene was found to have a C2v point group with an energy of 0.04879719 au, with ethene having an energy of 0.02619028. Identification of the Transition State using AM1 Semi-empirical TheoryOnce the HOMO and LUMO of the reactants had been computed the next step was to determine the transition state structure for the reaction path. The calculation was also undertaken using the AM1 semi-empirical method with a TS Berny setting on a transition state guess structure that had an envelope structure with maximal overlap between the π-orbitals of the ethene and the π-orbitals of the butadiene fragmnent. The distance between the ethene fragment and the terminal carbon atoms of the butadiene fragment were adjusted to 2.1 Å. The transition state structure was obtained and was confirmed by the presence of an imaginary vibrational mode at -956.10 cm-1 which corresponds to the correct motion expected when the two fragments come together. (However this mode is not part of the reaction coordinate.</span João (talk) 14:29, 28 December 2014 (UTC))
In the vibrational mode at -956.10 cm-1 it can be seen that the two fragments come together in a synchronous manner which would be expected, supporting a concerted mechanism. However, looking at the lowest real frequency at 147.73 cm-1 it is evident that there may be some asynchronous manner to the bond formation in the transition state as the two fragments are sliding over one another. As mentioned previously the molecular orbitals of butadiene and ethene come together to give a transition state structure with a particular conformation. According to Woodward-Hoffman rules (2), only molecular orbitals with the same symmetry can come together. As a result the LUMO of the transition state structure consists of the LUMO of cis-butadiene (diene) and the HOMO of ethene (dienophile), whereas the HOMO of the transition state structure is made up from the HOMO of cis-butadiene and the LUMO of ethene.
In the envelope transition state it can be seen that the bond length of the ethene fragment is smaller than the bond length for a sp3-sp3 C-C bond which has a value of 1.54 Å but it is slightly larger than a sp2-sp2 C=C bond, which has a bond length of 1.35 Å (6). This suggests that the distance between the two carbon atoms in the ethene fragment confirms that the bond is in a transition between a single and double bond. The bond distances between the two fragments (along the dashed lines - potential bonds) are 2.12 Å. This is significantly larger than a standard C-C bond. However, if the Van der Waals radii of a carbon atom is taken into account (1.7 Å), the covalent radii for a C-C single bond would equate to 3.4 Å, making the bond present in the transition state a favourable bonding interaction. It is also observed that the bond angles in the transition structure had changed from the reactants - there was a decrease in the H-C-C-H dihedral angles as a result of allowing the two fragments to approach one another with ease, minimising steric clash (see IRC animation).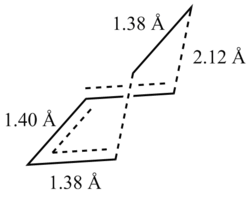 
Envelope Transition State for Diels Alder ReactionIRC Analysis of Reaction Pathway using AM1 Semi-empirical TheoryAn IRC analysis computing 150 steps using AM1 semi-empirical theory was conducted on the previously determined transition state in both directions of the potential energy surface, to compare the relationship between the reactant, transition state and the product of this Diels Alder reaction.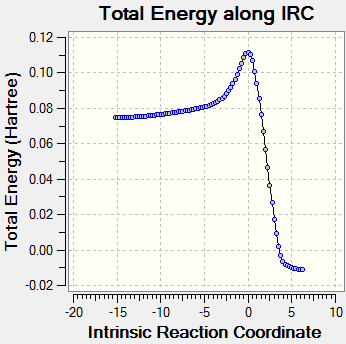 
 From the IRC profile it is evident that there is only one transition state involved in this reaction and it referred to as an 'early transition state' as it resembles the structure of the reactants more closely than it does of the product. The profile also shows that there is a relatively small activation energy and that the overall process is exothermic thus making it a thermodynamically favoured process (Would the thermodynamic viability of the process depend on entropic considerations and not only on energetic ones? João (talk) 14:29, 28 December 2014 (UTC)). The activation energy for this process can be found below and is calculated by subtracting the energies of the reactants from the energy of the transition state at both 0 K and 298.15 K.
Regioselectivity in Diels Alder Reaction of Cyclohexa-1,3-diene with Maleic anhydrideOptimisation of Cyclohexa-1,3-diene and Maleic AnhydrideAs conducted in the previous Diels Alder computational study the reactants, cyclohexa-1,3-diene and maleic anhydride were constructed separately on GaussView and optimised to a minimum individually using the AM1 semi-empirical method. The energy of maleic anhydride was computed to be -0.12182418 and that of cyclohexa-1,3-diene was 0.02795797. Once the fragments had been optimised their molecular orbitals were computed. 
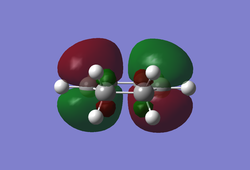
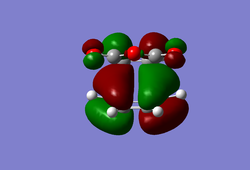
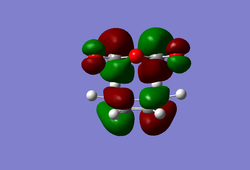
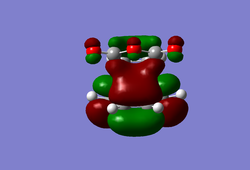
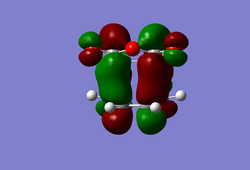
It can be seen that the cyclohexa-1,3-diene HOMO is anti-symmetrical with respect to the plane and the LUMO is symmetrical. However, for maleic anhydride the HOMO is anti-symmetrical (Isn't it symmetrical with respect to the vertical plane of symmetry? João (talk) 14:29, 28 December 2014 (UTC)) and the LUMO is also anti-symmetrical. As a result of this the HOMO-1 and HOMO-2 were investigated and it was found that the HOMO-1 was symmetrical with respect to the plane of symmetry and the HOMO-2 was also symmetrical with respect to the plane. This implies that the HOMO of cyclohexa-1,3-diene interacts with the LUMO of maleic anhydride as one would expect. This interaction is favoured due to the presence of oxygen atoms in the maleic anhydride which are electronegative and thus shift the LUMO to a lower energy state, leading to better overlap and enhanced stabilisation. However, instead of the LUMO of cyclohexa-1,3-diene interacting with the HOMO of maleic anhydride it instead interacts with the HOMO-2 in comparison to the HOMO-1 or HOMO to yield the correct molecular orbitals for the transition state. The reason why there is no interaction between the cyclohexa-1,3-diene HOMO and the maleic anhydride LUMO is because they do not have the same symmetry and thus this interaction is forbidden according to Woodward-Hoffman rules. Instead the LUMO interacts with the HOMO-2, even though it is the lowest in energy (leads to a weaker interaction) out of the three but it is symmetrical and so interactions are allowed. However, the driving force for this interaction is that there is also maximal orbital overlap leading to increased stabilisation of the molecular orbital and thus a favoured interaction in precedence to a possible alternative. Theoretically, the molecular orbitals involved in a chemical reaction are the HOMO and the LUMO of the reactants. This is not the case in this example and the reason for this could be a result of the unreliability of the computational techniques used as they consists of many approximations. Identifying the Endo Transition StateThe previously established optimised cyclohexa-1,3-diene and maleic anhydride reactants were combined together in GaussView to a form a guess structure for the endo transition state with the two fragments 2.1 Å apart at the site of bonding coordination. The strucutre was then optimised using the AM1 semi-empirical method with a TS Berny setting. The resulting transition state structure resembled that of the endo conformer with an energy of -0.05150470 and an imaginary frequency at -806.06 cm-1, confirming that the transition state has been located. 
 Geomteric analysis was performed on the endo transition state structure to identify whether any additional interactions could take place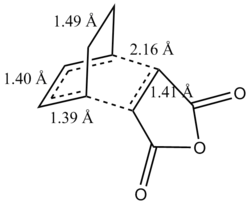 
Endo Transition State for Diels Alder ReactionIn addition to the bonds labelled in the above diagram it was noticed that there were through space interactions between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH=CH- for the endo which equated to 2.89 Å. This is indicative of some steric repulsion as the distance is less than the Van der Waal radii of two carbon atoms. Subsequently an IRC analysis was undertaken on the endo transition state structure in both directions using an AM1 semi-empirical method to see how the reaction path proceeds from the reactants to the products. 
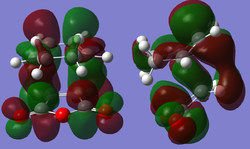
 (In the images above you cyclohexadiene seems to have a C2v geometry. Would this be the most stable configuration of this reactant? João (talk) 14:29, 28 December 2014 (UTC)) It can be seen that the reaction is exothermic and is thus thermodynamically favoured, with the energy of the product being lower than that of the reactants. Analysing the molecular orbital of the endo transition it is clear that there are some secondary orbital overlaps between the C=C double bond of the cyclohexadiene and the C=O bonds found on the maleic anhydride. These interactions appear as a result of π-π* orbital interactions, with the π* orbital being located on the C=O bond as the oxygen atom is electronegative, withdrawing electron density from the bond and lowering the energy of the π* orbital. These secondary orbital overlaps are theoretically supposed to occur in the HOMO of the molecule (Did you check for such an effect in orbitals bellow the HOMO in energy? João (talk) 14:29, 28 December 2014 (UTC)), however it is apparent from the diagrams below that these interactions are only visible in the LUMO+1 and LUMO+2 orbitals. A possible explanation for this is that as we are considering a transition state structure, we can assume that the electrons are not localised to specific bonds but they are delocalised with the entirety of the structure and can thus exist in the LUMO+1 and LUMO+2.
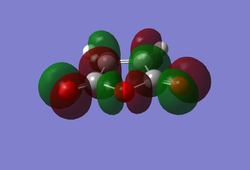
Identifying the Exo Transition StateThe previously established optimised cyclohexa-1,3-diene and maleic anhydride reactants were combined together as done when locating the endo transition state however in this case they were oriented differently such that the C=O groups of the maleic anhydride were not directly above or below the C=C in cyclohexadiene. The two fragments were still kept at 2.1 Å apart at the site of bonding coordination. The strucutre was then optimised using the AM1 semi-empirical method with a TS Berny setting. The resulting transition state structure resembled that of the endo conformer with an energy of -0.05041983 and an imaginary frequency at -812.33 cm-1, confirming that the transition state has been located.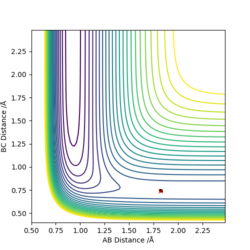 
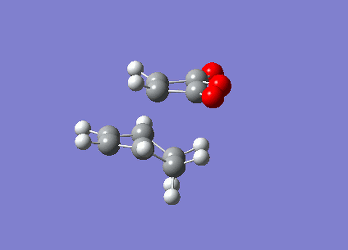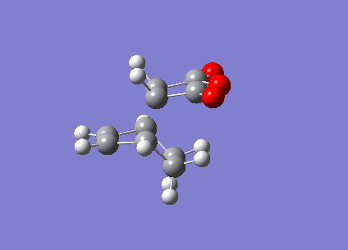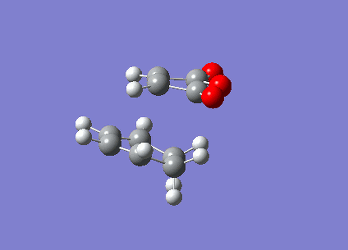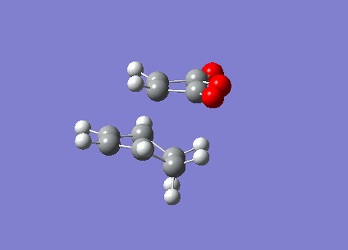 Geomteric analysis was performed on the endo transition state structure to compare the effects of secondary interactions and steric repulsion to see which one has a determining factor on the energy of the transition state.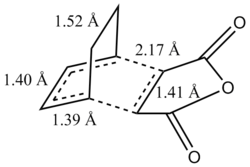 
Exo Transition State for Diels Alder ReactionThere were also through space interactions between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH2-CH2- for the exo confomer which equated to 2.95 Å (Shouldn't you be comparing to the H atom which is closer? João (talk) 14:29, 28 December 2014 (UTC)). This suggests that the exo conformation of the transition state is slightly more strained and experiences a greater steric repulsion between the two fragments, resulting in a slightly elongated distance between the two fragments. This steric repulsion is present in the endo structure of the transition state however it is compensated for by the potential secondary orbital interactions that exist (7). An IRC analysis was not run on the exo transition state as one can assume that if the correct transition state structure was obtained for the endo product simply using a semi-empirical TS Berny optimisation method then the computation would yield the correct structure for the exo transition state and thus be a transition state that connects the reactants to the products. The molecular orbital for the exo transition state were finally examined and orbitals all showed the same overall symmetry when compared with the molecular orbitals of the endo transition state. The only anomalous feature of these orbitals was that when you went up to the LUMO+1 and LUMO+2 secondary orbital overlaps were also observed, however they are not expected to be present due to the orientation of the two fragments
The final calculation to be conducted was the activation energies of both reaction pathways involving the reaction including cyclohexa-1,3-diene and maleic anhydride, one of which occurs through an exo transition state whilst the other occurs through an endo transition state. From determining the thermochemical data for the reactants and both possible transition states it was a lot easier to compare the difference in stability between the two and the preference for the reaction to proceed down one pathway compared to another.
It is evident from the data above that the there is a preference for the Diels Alder reaction to proceed via the endo transition state to form the endo product as it is lower in energy, with a lower activation barrier and thus easier for the reaction pathway to follow this route - the endo transition state is 0.87 kcal/mol lower in energy than the exo transition state. The cause of this lower transition state can be explained due to the secondary orbital overlap that is present between the C=O bonds of the maleic anhydride (dienophile) and the C=C double bond of the diene. This reaction pathway follows normal electron demand where HOMO of the diene interacts with the LUMO of the dienophile and vice versa. ConclusionIn conclusion, these computational methods were extremely successful in optimising and locating transition structures on a potential energy surface for various pericyclic reactions. Each computational technique however has some disadvantages as not every factor has been taken into account. These include solvent effects as well as optimising structures in the presence of other chemical species, as in standard laboratory conditions this is unlikely. References1. Carey, F.A. and R.J. Sundberg. Advanced Organic Chemistry Part A
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
_final_motion2.gif)
_modifiedboat_vibration2.gif)
identified2.gif)
identified2.gif)
.png)
.png)
.png)
.png)
