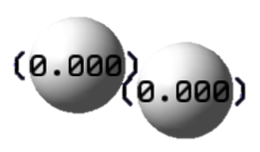Rep:Mod:AKH7493
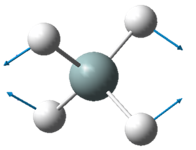
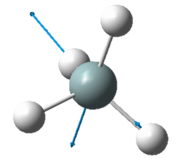
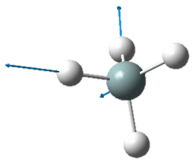
NH3
Item Table
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986280D-10 Optimization completed.
-- Stationary point found.
| category | information |
|---|---|
| Molecule | NH3 |
| Calculation Method | B3LYP |
| Basis set | 6-31G(d,p) |
| Final Energy in au | -56.5577687 |
| RMS Gradient in au | 0.00000485 |
| Point group | C3v |
| Property | Value | unit |
| N-H bond distance | 1.01798 | Ångströms |
| H-N-H bond angle | 105.741 | Degrees |
Jmol
NH3 |
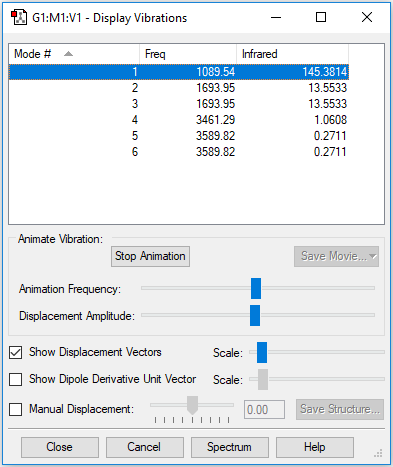
Vibrations
| Image |  |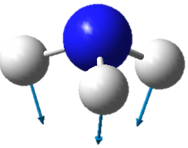
 |
|
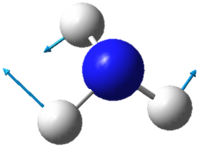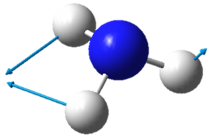
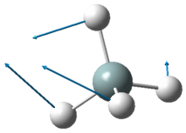
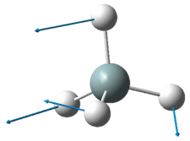
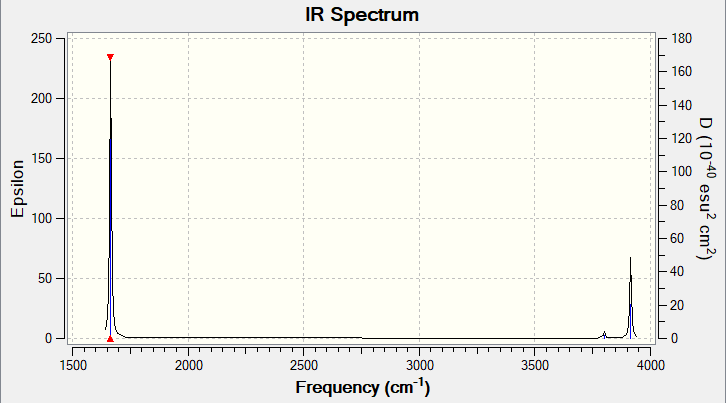
| Wavenumber in cm-1 | 1090 | 1694 | 1694 |
| Symmetry | A1 | E | E |
| Intensity | 145 | 14 | 14 |
| Image |  |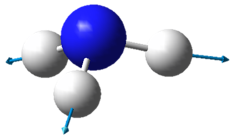
 |
|
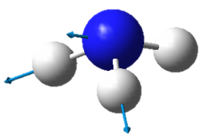
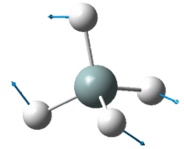
| Wavenumber in cm-1 | 3461 | 3590 | 3590 |
| Symmetry | A1 | E | E |
| Intensity | 1 | ~0 | ~0 |
How many modes are expected from the 3N-6 rule?
Ammonia consists of 4 atoms, so the 3N-6 rule gives 3*4-6=6 vibrational modes in the molecule.
Which modes are degenerate (ie have the same energy)?
The two pairs of vibrational modes with 1694 cm-1 and 3590 cm-1 are degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
The lowest energy vibrational modes with wavenumbers 1090cm-1 and 1694cm-1 are bending vibrations, whereas the more energetic vibrations with wavenumbers 3461 cm-1 and 3590 cm-1 are stretching modes.
Which mode is highly symmetric?
The 3461 cm-1 vibration is highly symmetric.
One mode is known as the "umbrella" mode, which one is this?
The 1090 cm-1 bending mode is known as the "umbrella" mode.
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
I would expect to see two bands in the experimental spectrum of gaseous ammonia. The energetic stretching modes do not involve a change in dipole moment, and are IR inactive. This is in correspondence with the calculated IR intensities of the stertching modes which are almost zero. The two degenerate 1694 cm-1 modes of vibration will contribute to the same band, and the 1090 cm-1 mode will produce the second strong band.
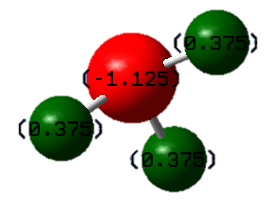
Charge Distribution
Using the "charge distribution" option in Gaussian, the calculated charges were found to be 0.375 e for each H-atom and -1.125 e for the N-atom. As the Pauling electronegativity of Nitrogen is higher (3.04) than Hydrogen (2.20), this result was expected.
H2
Item Table
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-1.164080D-13 Optimization completed. -- Stationary point found.
| category | information |
|---|---|
| Molecule | H2 |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final Energy in au | -1.17853936 |
| RMS Gradient in au | 0.000000172 |
| Point group | D∞h |
| Property | Value | unit |
| Bond distance | 0.74279 | Ångströms |
Jmol
H2 |
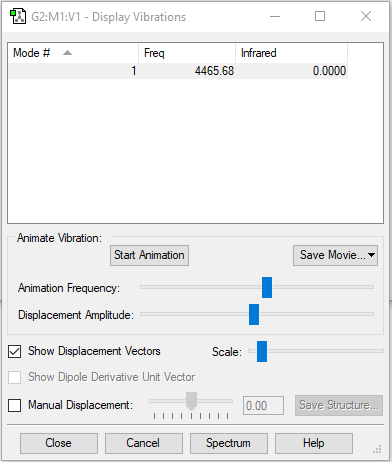
Vibrations
| Image |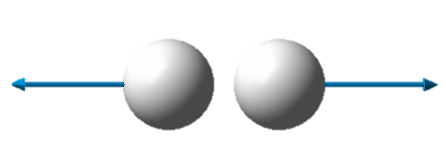 
|
| Wavenumber in cm-1 | 4466 |
| Symmetry | SGG |
| IR intensity | 0 |
Charge Distribution
The charges on the Hydrogen atoms are 0; the H-H bond is purely covalent.
N2
Item Table
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES Predicted change in Energy=-3.401096D-13 Optimization completed. -- Stationary point found.
| category | information |
|---|---|
| Molecule | N2 |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final Energy in au | -109.5241286 |
| RMS Gradient in au | 0.00000060 |
| Point group | D∞h |
| Property | Value | unit |
| Bond distance | 1.10550 | Ångströms |
Jmol
N2 |
Vibrations
| Image |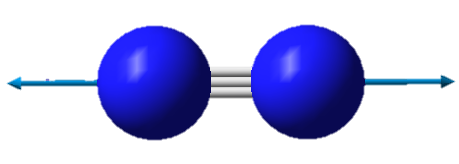 
|
| Wavenumber in cm-1 | 2457 |
| Symmetry | SGG |
| IR intensity | 0 |
Charge Distribution
The charges on the Nitrogen atoms are 0, the bond is purely covalent.
N2 as ligand in TM complex
PAKVEF 1.118 Angstrom Using ConQuest to search for a mono-metallic transition metal complex that coordinates N2, this Cobalt complex was found: [PAKVEF]
Through X-ray diffraction, the dinitrogen bond length in the complex is found to be 1.118 Å, which is higher than the computed value of 1.055 Å. This can be rationalized by considering the electron withdrawing effect of Co. The calculation gives a lower bond distance estimate as it considers isolated N2. When N2 is bonded to the transition metal, the electron density between the nitrogen atoms and thus the bond strength is reduced. This gives a weaker and longer bond.
The Haber-Bosch process
In the Haber-Bosch process, nitrogen and hydrogen gas react to form ammonia:
N2 + 3H2 → 2NH3
The calculated energies of the reaction component are:
E(NH3) = -56.5577687 au
2*E(NH3) = -113.115537 au
E(N2) = -109.5241286 au
E(H2) = -1.17853936 au
3*(H2) = -3.5356181 au
ΔE = 2*E(NH3) - [E(N2) + 3*E(H2)] = -0.563284 au
ΔE = -0.563284 au * 2625.5 (kJ/mol)/au = -147.9 kJ/mol
The reaction is exothermic. This means that heat energy is released when nitrogen and hydrogen gas react to form ammonia, which again means that the ammonia product is more stable energetically than the geaseous reactants.
Project Molecule: Silane
Item Table
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES Predicted change in Energy=-2.449663D-14 Optimization completed. -- Stationary point found.
| category | information |
|---|---|
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final Energy in au | -291.88802760 |
| RMS Gradient in au | 0.00000002 |
| Point group | Td |
| Property | Value | unit |
| Si-H bond distance | 1.48485 | Ångströms |
| H-Si-H bond angle | 109.471 | Degrees |
Jmol
SiH4 |
Vibrations
| Image |  |
 |
|
| Wavenumber in cm-1 | 919 | 919 | 919 |
| Symmetry | T2 | T2 | T2 |
| Intensity | 136 | 136 | 136 |
| Image |  |
 |
|
| Wavenumber in cm-1 | 979 | 979 | 2244 |
| Symmetry | E | E | A1 |
| Intensity | 1 | ~0 | ~0 |
| Image |  |
 |
|
| Wavenumber in cm-1 | 2256 | 2256 | 2256 |
| Symmetry | T2 | T2 | T2 |
| Intensity | 143 | 143 | 143 |
SiH4 Charge Distribution
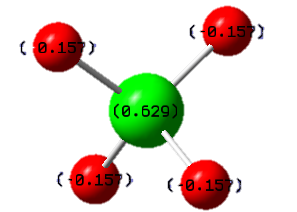
The charges on silicon and hydrogen in SiH4 were found to be 0.629 e and -0.157 e respectively using the NBO function in Gaussian. This is very different from the isoelectric methane, in which the central carbon atom is negatively charged. This stems from the fact that silicon (χ=1.9) is less electronegative than hydrogen (χ=2.20) which again is less electronegative than carbon (χ=2.55).
Molecular orbitals of SiH4
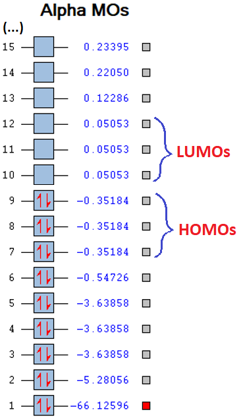
| Image |  |
 |
 |
 |
|
|---|---|---|---|---|---|
| Energy
in au |
-3.63858 | -0.54726 | -0.35184 | 0.05053 | 0.12286 |
| Bonding
property |
Non-bonding | Bonding | Bonding (HOMO) | Anti-bonding (LUMO) | Anti-bonding |
| Symmetry | T2 | A1 | T2 | T2 | A1 |
The first chosen molecular orbital of SiH4 is a low-energy non-bonding orbital. Judging from its shape and size, the major contribution is from the silicon 2p atomic orbital. This explains why it has to degenerate MO's with different orientations. The next molecular orbital has a large positive effect on the bonding of silane. It stems from the in-phase mixing of the Si 3s atomic orbital with the 1s H atomic orbitals. The antibonding orbital of this MO is the last in the table above, and is a result of the out-of-phase mixing of silicons 3s AO with the in-phase 1s AOs of hydrogen. It has one radial node, and is much higher in energy.
The shape of the HOMO can be explained by considering the combination of the four hydrogen 1s AO where two and two are in the same phase. This percieved combination of AOs has the correct symmetry to interact with a 3p AO on silicon in a contructive manner in which the two lobes of the 3p AO combines in phase with one pair of 1s AOs each. The LUMO can be considered as the antibonding of the HOMO. It is formed by the destructive version of the described interaction, and decreases the contructive interference between the lobes of the 3p AO with the same phase 1s AOs. Both the HOMO and the LUMO has two other degenerate forms with the same shape but different orientations in space. This is due to the fact that there are 3 degenerate silicon 3p AOs and many ways of arranging the hydrogen 1s AOs.
Independent work- H2O
Item table
| category | information |
|---|---|
| Calculation Method | B3LYP |
| Basis set | 6-31G(d,p) |
| Final Energy in au | -76.41973740 |
| RMS Gradient in au | 0.00006276 |
| Point group | C2v |
| Property | Value | unit |
| O-H bond distance | 0.96522 | Ångströms |
| H-O-H bond angle | 103.745 | Degrees |
Jmol
H2O |
Vibrations
| Wavenumber in cm-1 | 1665 | 3801 | 3914 |
| IR Intensity (arbitraty unit) | 70 | 2 | 20 |
Predicted IR Spectrum of H2O
Molecular Orbitals of H2O
I will use data from the H2O optimisation in Gaussian to determine whether or not the two lone pairs on oxygen in the Lewis structure of H2O are degenerate.
Calculated molecular orbitals
AO contributions from LOG file
| Image |  |
|
|---|---|---|
| Energy in au | -0.37102 | -0.29197 |
| Type of molecular orbital | Slight bonding character | Non-bonding |
| AO contribution | 55.43% H 1s and 44.5% O 2py | ~100% O 2px |
The calculated MOs of the water molecule suggest that the two lone pairs are electron pairs in the highest energy occupied orbitals of the molecule. The HOMO is the highest energy lone pair and has most contribution from the 2px AO of oxygen which does not have the correct symmetry to interact with the 1s hydrogen orbitals.
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES - very good structure and through explanations. The marks you have lost are entirely due to the lack of links to your log files, everything else is very good well done!
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 0/1
Have you completed the calculation and given a link to the file?
No - you didn't include a direct link to the file!
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES but you didn't include a direct link to the files!
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 4/5
Have you completed the calculation and included all relevant information?
YES - no link to the log file though!
Have you added information about MOs and charges on atoms?
YES - very good explanations well done.
Independence 1/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or
YES
Do an extra calculation on another small molecule, or
YES
Do some deeper analysis on your results so far
YES