Rep:Mod:AHall Computational Lab Module 1
Molecular Mechanics Modeling
Hydrogenation of Cyclopentadiene Dimer
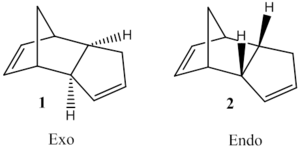
The exo and endo dimers of cyclopentadiene were optimised using a MM2 forcefield. The calculated energies of the two dimers were 31.8764 and 33.9975 kcal/mol for exo/endo respectively:
EXO ------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 2: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.2851 Bend: 20.5804 Stretch-Bend: -0.8381 Torsion: 7.6555 Non-1,4 VDW: -1.4173 1,4 VDW: 4.2333 Dipole/Dipole: 0.3775 Total Energy: 31.8764 kcal/mol Calculation completed ------------------------------------ ENDO ------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 2: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.2509 Bend: 20.8475 Stretch-Bend: -0.8358 Torsion: 9.5109 Non-1,4 VDW: -1.5439 1,4 VDW: 4.3202 Dipole/Dipole: 0.4476 Total Energy: 33.9975 kcal/mol Calculation completed ------------------------------------
The energy for the endo form of the cyclopentadiene dimer is more positive than the exo form, indicating a lower stability. This observation implies that for this reaction the thermodynamic product is the exo form, however the reaction exclusively produces the endo form, which is explained by consideration of the secondary orbital interaction during the transition state.[1] As the favoured product is not the most stable one the mechanism must be under kinetic control.
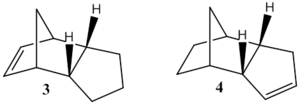

3 ------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 2: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.2768 Bend: 19.8598 Stretch-Bend: -0.8345 Torsion: 10.8076 Non-1,4 VDW: -1.2214 1,4 VDW: 5.6345 Dipole/Dipole: 0.1621 Total Energy: 35.6850 kcal/mol Calculation completed ------------------------------------ 4 ------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 103: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.0965 Bend: 14.5258 Stretch-Bend: -0.5492 Torsion: 12.4969 Non-1,4 VDW: -1.0714 1,4 VDW: 4.5128 Dipole/Dipole: 0.1406 Total Energy: 31.1520 kcal/mol Calculation completed ------------------------------------
Of the two double bonds, the hydrogenation of the bond away from the bridging carbon (structure 3) is less favourable than the hydrogenation of the double bond near to the bridge (structure 4). Of the factors that are used to calculate the total energy, there is a large difference in the bending, torsion and Van-der-Waals energies, with other smaller changes in the stretching and dipole energies.
The removal of either double bond leads to a reduction in the torsional strain of the molecule compared to the un-hydrogenated cyclopentadiene dimer. The decrease in torsional strain is greatest for the hydrogenation of the double bond away from the bridge as hydrogenating this bond allows the ring to distort, minimising the torsion. The double bond closer to the bridge is still constrained by the bridge, so there is less change in torsional strain.
The largest difference is for bending energy, as structure 3 has a much greater bending energy than structure 4. Hydrogenating the double bond closest to the bridge allows this ring to twist, which is normally prevented by the double bond. Hydrogenating the double bond away from the bridge also allows twisting of the ring, however this twisting is also possible to a certain extent in the unsaturated form, so the change in bending energy from hydrogenating this bond is not as significant as hydrogenating the double bond closest to the bridge.
Taxol
Two intermediates in the synthesis of taxol are shown below (structures 9 and 10). Each structure was minimised using the MM2 force field.
| Taxol Intermediate 9 | Taxol Intermediate 10 | ||||||
|---|---|---|---|---|---|---|---|
|
| ||||||
| 47.8395 kcal/mol | 42.6828 kcal/mol |
Structure 9 ------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 2: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.7847 Bend: 16.5413 Stretch-Bend: 0.4304 Torsion: 18.2513 Non-1,4 VDW: -1.5528 1,4 VDW: 13.1094 Dipole/Dipole: -1.7248 Total Energy: 47.8395 kcal/mol Calculation completed ------------------------------------ Structure 10 ------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 178: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.6196 Bend: 11.3410 Stretch-Bend: 0.3433 Torsion: 19.6706 Non-1,4 VDW: -2.1616 1,4 VDW: 12.8723 Dipole/Dipole: -2.0022 Total Energy: 42.6829 kcal/mol Calculation completed ------------------------------------
These results show that structure 10 is lower in energy than structure 9. The largest difference in the contributing energies is from the bending energies, which may be due to the angle that the cyclohexane ring is forced to adopt by the carbonyl (in plane for structure 10 and pointing downwards for structure 9) restricting the bending of the cyclohexane in structure 9, causing the bending energy to be higher.
These intermediates are an example of hyperstable alkenes. A hyperstable alkene is an alkene which is stabilised with respect to the parent alkane, (the calculated energy of the saturated form of structure 9 is 62.5043 kcal/mol) leading to increased experimental stability and decreased reactivity.[2][3] Hyperstable alkenes are found at bridgeheads in medium sized rings such as the taxol intermediates 9 and 10. These alkenes are particularly stable due to the ring structure requiring a bond angle closer to 120° than 109°, and so favouring the sp2 alkene over the sp3 centred alkane. Small rings cannot support bridgehead alkenes as the ring strain induced would cause the desired bond angle to be <100°, and so the alkene would be strongly disfavoured, with the alkane form being much more stable.
The optimisation was repeated using the MMFF94 force field to compare how the energies differed. Whilst it is not possible to directly compare the energies between different force fields, it can be observed that the same pattern of stability is present, with the intermediate 10 being the lower energy form.
- Intermediate 9: 70.5284 kcal/mol
- Intermediate 10: 60.5445 kcal/mol
Addition of Dichlorocarbene to a diene
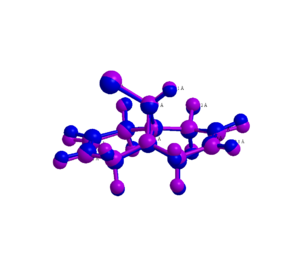
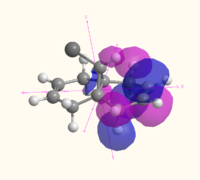
Molecule 12 is a diene which can interact with electrophillic reagents including carbenes. The geometry of structure 12 was optimised using the MM2 and MOPAC methods and the geometries compared. As can be seen from the overlaid structures (see image to right), the MM2 (purple) and MOPAC (blue) geometries are not identical, particularly with respect to the positions of the hydrogen atoms. The MOPAC geometry has a greater bending of the rings than the MM2 geometry and also has slightly shorter bond lengths (eg. for C-H MOPAC is 1.0946Å compared to 1.1035Å for MM2). The biggest difference in geometries is for the alkene hydrogens as the bending of the ring moves the outermost atoms more than the inner atoms.
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 182: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 0.6187 Bend: 4.7352 Stretch-Bend: 0.0399 Torsion: 7.6605 Non-1,4 VDW: -1.0664 1,4 VDW: 5.7941 Dipole/Dipole: 0.1123 Total Energy: 17.8945 kcal/mol Calculation completed ------------------------------------
------------ Mopac Interface ------------ Model: AHall_diene_MM2 Mopac Job: AUX RM1 CHARGE=0 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.07953 (< 0.10000) Heat of Formation = 22.82757 Kcal/Mol -----------------------------------------
MO Calculations
Gaussian
------------ Gaussian Interface ------------ Model: AHall_diene_MOPAC_2 1) Gaussian Job: # B3LYP/6-31G Test Charges (Electron Density): C(1) 4.962337 C(2) 4.932324 C(3) 5.141098 C(4) 5.499868 C(5) 5.499868 C(6) 5.128338 C(7) 5.141172 C(8) 4.932342 C(9) 4.962394 C(10) 5.128336 C(11) 5.958274 Cl(12) 16.935732 H(13) 0.599510 H(14) 0.609465 H(15) 0.613754 H(16) 0.607330 H(17) 0.609378 H(18) 0.620105 H(19) 0.607301 H(20) 0.613753 H(21) 0.609466 H(22) 0.599540 H(23) 0.609353 H(24) 0.620075 H(25) 0.522183 Charges (Mulliken Charges): C(1) -0.107045 C(2) -0.085159 C(3) -0.306433 C(4) 0.062963 C(5) 0.062963 C(6) -0.296953 C(7) -0.306490 C(8) -0.085166 C(9) -0.107058 C(10) -0.296932 C(11) -0.387676 Cl(12) 0.044633 H(13) 0.120357 H(14) 0.112346 H(15) 0.145582 H(16) 0.144803 H(17) 0.147728 H(18) 0.136007 H(19) 0.144818 H(20) 0.145607 H(21) 0.112348 H(22) 0.120340 H(23) 0.147720 H(24) 0.136016 H(25) 0.194683 Gaussian Interface: Dipole = (-1.9036, 0.0012, -1.4709) 2.4056 Debye Gaussian Interface: SCF Energy = -556594.14 Kcal/Mol --------------------------------------------
MOPAC
------------ Mopac Interface ------------ Model: AHall_diene_MOPAC_2 Mopac Job: RM1 CHARGE=0 EF GNORM=0.100 GRAPH SHIFT=80 Mopac Interface: Core-Core Repulsion = 9301.92140 eV Mopac Interface: COSMO Area = 195.06 A^2 Mopac Interface: COSMO Volume = 214.38 A^3 Mopac Interface: Dipole = (1.245, -0.034, -1.811) 2.198 Debye Mopac Interface: Electronic Energy = -11247.57545 eV Mopac Interface: Heat of Formation = 22.82755 Kcal/Mol Mopac Interface: Ionization Potential = 9.114060 eV Mopac Interface: Molecular Weight = 180.677 Mopac Interface: Total Energy = -1945.65405 eV Finished @ RMS Gradient = 0.07257 (< 0.10000) Heat of Formation = 22.82755 Kcal/Mol -----------------------------------------
Comparison
The MOs of molecule 12 are shown in the table below as calculated using Gaussian (B3LYP/6-31G(d,p)), MOPAC (RM1) and Huckel methods. The Gaussian MOs include a 3D rotatable model which can be accessed by the links next to the pictures:
| Gaussian (B3LYP/3-61G) | MOPAC (RM1) | Huckel | |
|---|---|---|---|
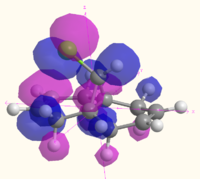
| LUMO+2 | 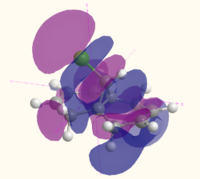 MO 51 MO 51 |
 |
|
| LUMO+1 | 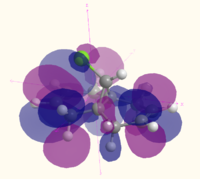 MO 50 MO 50 |
 |
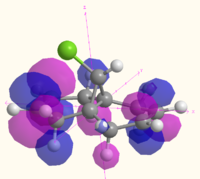
|
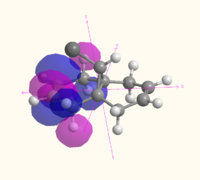
| LUMO |  MO 49 MO 49 |
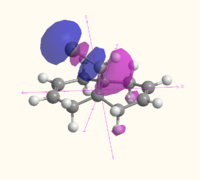 |
|
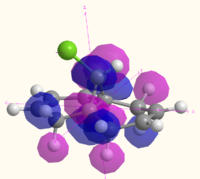
| HOMO |  MO 48 MO 48 |
 |
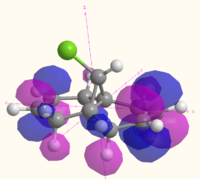
|
| HOMO-1 |  MO 47 MO 47 |
 |
|
| Total No. MOs | 98 | 61 | 61 |
The MOs illustrate the symmetry present in the molecule, as whilst there is a plane of symmetry (with respect to the shape of the orbitals, the phase of the orbitals is inverted) that passes through the two double bonds and the chlorine atoms, the two double bonds are not equal. The chlorine atoms appears to play a large role in the MOs of the alkene on the same side of the molecule, with the HOMO-1, HOMO, LUMO and LUMO+1 all showing interactions with the chlorine that are not present for the other alkene and the hydrogen atom on the bridge. The electron density of the alkenes also varies with more electron density on the chlorine side for the HOMO and LUMO-1, and more electron density on the side away from the chlorine for the HOMO-1 and LUMO. The LUMO+2 clearly shows the σ* anti-bonding interaction of the C-Cl bond.
The difference between the different calculation methods appears to be mainly in the ordering of the orbitals. The HOMO-1 has similar shaped orbitals for both the Gaussian and MOPAC calculations, however the Huckel calculation has a very different shape, which may be due to a different ordering of the orbitals. The HOMO appears the same in all calculation methods, however the LUMO is very different. The shape of the MOs in the LUMO are the same for the Gaussian calculation as for the Huckel calculation (however the Huckel calculation does not take into account the mixing very well). The shape of the LUMO from the MOPAC calculation is much closer to the LUMO+2 for the Gaussian calculation, and is most likely to be due to a reordering of the orbitals depending on the energy that the method calculated. The MOPAC LUMO+1 is the closest match to the Gaussian LUMO, and again the shape of the Gaussian MO is closely matched by the Huckel calculation. The LUMO+2 shows the biggest variation in shape, with the Gaussian calculation showing the σ* of the C-Cl bond, the MOPAC calculation showing the anti-bonding π* of the alkene closest to the chlorine, and the Huckel calculation showing an entirely different MO which does not have electron density on chlorine or the alkenes.
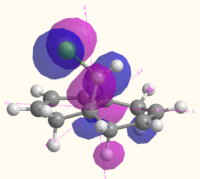
Molecular Electrostatic Potential

The Molecular Electrostatic Potential (MEP) was also calculated in Gaussian (Jmol image below; red=positive charge, blue=negative charge). The MEP was also calculated in MOPAC as shown in the image to the right. The surface shows that there is a much bigger difference in negative potential over the double bond closest to the chlorine. The MEP also indicates a strong contribution from the chlorine atom, as a significant amount of the negative charge is localised on the chlorine atom due to the lone electron pairs. The MOPAC MEP also shows a greater density of negative charge over the alkene on the chlorine side, however the electron density on the chlorine atom itself is not calculated.
Orbital |
Vibrational Analysis
Vibrational analysis was carried out using the B3LYP/6-31G(d,p) method. The output files can be found at DOI:10042/24373 . The low frequencies are shown below:
Low frequencies --- -5.4985 -0.0004 0.0018 0.0018 7.5241 10.6316 Low frequencies --- 90.2563 125.6213 158.1295
A total of 69 vibrations are calculated, however only those with intensity of >50% are shown here.
| Vibration Number | Frequency /Hz | Intensity | Animation |
|---|---|---|---|
| 18 | 689.48 | 53.3591 | 
|
| 55 | 1737.03 | 4.1981 | 
|
| 56 | 1757.34 | 3.9363 | 
|
| 59 | 3009.68 | 100.7981 | 
|
| 63 | 3033.66 | 62.7628 | 
|
| 67 | 3176.22 | 54.6718 | 
|
Vibrations 55 and 56 are stretches of the C=C bond. It is interesting to note that the stretch for the C=C bond closest to the chlorine occurs 10cm-1 higher in frequency than the stretch for the other double bond. This may be caused by stablisisation of the double bond by interaction with the chlorine as shown in the HOMO-1 MO.
The vibrations with intensity >50% are all either bending or stretching motions of the hydrogen atoms - there are very few vibrational modes assoiciated with the carbon framework or the C-Cl bond. The carbon framework is held fairly rigidly in shape by the double bonds and tricyclic nature, restricting its motion so any vibrations including the framework are very low in intensity.
Sugars
Intermediate A Optimisation
(Click on titles to view 3D structures)
Acetyl up, Carbonyl up
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 685: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.4447 Bend: 14.6039 Stretch-Bend: 0.9110 Torsion: 2.9291 Non-1,4 VDW: 0.1601 1,4 VDW: 19.7860 Charge/Dipole: -27.5555 Dipole/Dipole: 8.3385 Total Energy: 21.6178 kcal/mol Calculation completed ------------------------------------ ------------ Mopac Interface ------------ Model: AHall_sugarA_u_u.mol Mopac Job: AUX PM6 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.08425 (< 0.10000) Heat of Formation = -67.13110 Kcal/Mol -----------------------------------------
Acetyl up, Carbonyl down
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 278: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.3734 Bend: 11.7761 Stretch-Bend: 0.8360 Torsion: 3.0796 Non-1,4 VDW: -0.7500 1,4 VDW: 19.8635 Charge/Dipole: -24.6139 Dipole/Dipole: 6.5015 Total Energy: 19.0663 kcal/mol Calculation completed ------------------------------------ ------------ Mopac Interface ------------ Model: AHall_sugarA_u_d.mol Mopac Job: AUX PM6 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.08489 (< 0.10000) Heat of Formation = -76.46707 Kcal/Mol -----------------------------------------
Acetyl down, Carbonyl up
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 675: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.1600 Bend: 11.9305 Stretch-Bend: 0.8274 Torsion: 3.2232 Non-1,4 VDW: -1.3435 1,4 VDW: 19.8651 Charge/Dipole: -28.5068 Dipole/Dipole: 5.9009 Total Energy: 14.0568 kcal/mol Calculation completed ------------------------------------ ------------ Mopac Interface ------------ Model: AHall_sugarA_d_u.mol Mopac Job: AUX PM6 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.09677 (< 0.10000) Heat of Formation = -85.04659 Kcal/Mol -----------------------------------------
Acetyl down, Carbonyl down
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 2: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.2850 Bend: 15.5319 Stretch-Bend: 0.9518 Torsion: 0.5811 Non-1,4 VDW: -1.5420 1,4 VDW: 18.7919 Charge/Dipole: -24.1310 Dipole/Dipole: 9.8639 Total Energy: 22.3326 kcal/mol Calculation completed ------------------------------------ ------------ Mopac Interface ------------ Model: AHall_sugarA_d_d.mol Mopac Job: AUX PM6 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.06685 (< 0.10000) Heat of Formation = -75.90748 Kcal/Mol -----------------------------------------
Intermediate B Optimisation
(Click on titles to view 3D structures)
Both on bottom face
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 2: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.9565 Bend: 12.9781 Stretch-Bend: 0.7430 Torsion: 7.8213 Non-1,4 VDW: -3.6683 1,4 VDW: 17.6506 Charge/Dipole: -2.9956 Dipole/Dipole: 0.3778 Total Energy: 34.8635 kcal/mol Calculation completed ------------------------------------ ------------ Mopac Interface ------------ Model: AHall_sugarB_d_d.mol Mopac Job: AUX PM6 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.09056 (< 0.10000) Heat of Formation = -88.06989 Kcal/Mol -----------------------------------------
C-O down, C=O up
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 545: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.9320 Bend: 19.7526 Stretch-Bend: 0.8829 Torsion: 5.4103 Non-1,4 VDW: -3.2338 1,4 VDW: 18.5260 Charge/Dipole: -1.2288 Dipole/Dipole: -0.0293 Total Energy: 43.0119 kcal/mol Calculation completed ------------------------------------ ------------ Mopac Interface ------------ Model: AHall_sugarB_d_u.mol Mopac Job: AUX PM6 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.09707 (< 0.10000) Heat of Formation = -66.86420 Kcal/Mol -----------------------------------------
Both on top face
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 795: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.7912 Bend: 22.7092 Stretch-Bend: 0.7541 Torsion: 7.4668 Non-1,4 VDW: -2.1619 1,4 VDW: 16.9664 Charge/Dipole: -23.8443 Dipole/Dipole: 1.1740 Total Energy: 24.8554 kcal/mol Calculation completed ------------------------------------ ------------ Mopac Interface ------------ Model: AHall_sugarB_u_u.mol Mopac Job: AUX PM6 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.08259 (< 0.10000) Heat of Formation = -91.64154 Kcal/Mol -----------------------------------------
C-O up, C=O down
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 503: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.6686 Bend: 19.9984 Stretch-Bend: 0.7825 Torsion: 6.3093 Non-1,4 VDW: -2.7712 1,4 VDW: 18.4537 Charge/Dipole: -6.1437 Dipole/Dipole: 0.5719 Total Energy: 39.8695 kcal/mol Calculation completed ------------------------------------ ------------ Mopac Interface ------------ Model: AHall_sugarB_u_d.mol Mopac Job: AUX PM6 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.09598 (< 0.10000) Heat of Formation = -65.46929 Kcal/Mol -----------------------------------------
Comparison
Intermediate A
For the structures where the acetyl group is attached to the top face of the sugar, both the MM2 and PM6 calculations show that the most favourable conformation is where the carbonyl group is pointing downwards. This may be due to the steric repulsion of the methyl group, which is lower for the form where the carbonyl points downwards as the methyl group points away from the rest of the molecule. The contributions towards the MM2 energy show that the biggest differences are for the bending energy and for the dipole interactions. When the carbonyl is pointing down there is a potentially favourable 2.2Å O...H interaction possible which may contribute towards the reduced dipole-dipole energies and the increased stability of the molecule.
The structures where the acetyl group is attached to the bottom face are the more favourable configuration, mainly because the ring conformation allows the terminal OMe group to twist around over the top of the oxenium cation, presumably stabilising the charge by donation of electron density from the oxygen lone pairs. Of the two configurations of the carbonyl group the most stable form is when the carbonyl is pointing upwards (this is the most stable form overall. The major contributions to this lower energy are the same as for the first pair of molecules, with the bending and dipole energies being the biggest changes. This is also likely to be due to stabilising interactions of the oxygen with nearby hydrogens and the location of the methyl group away from the rest of the molecule.
When considering the most stable form of the two stereoisomers (acetyl up, carbonyl down) and (acetyl down, carbonyl up) using the MM2 and PM6 methods it is found for the acetyl up, carbonyl down form the MM2 method gives the C-O bond from the acetyl group to the ring as 1.4108Å whereas the PM6 method has this bond as 1.4258Å. The C-O-C bond angle is also different at 118.6134° for the MM2 method and 117.0197° for PM6. The C-O+=C bond angle shows the biggest difference at 128.8951° for MM2 and 122.2478° for PM6. In general the bonds are all slightly shorter for PM6 than MM2.
For the acetyl down, carbonyl up version the C-O+=C bond angle is 129.6622° for MM2 and 107.7615° for PM6, with the O+=C bond 0.1374Å shorter (1.2242Å for MM2 compared to 1.3616Å for PM6). These changes can be explained by the interaction of the terminal OMe group donating electron density to the oxenium ion and so weakening the C=O bond and making the geometry closer to sp3 which is present in the PM6 calculation but not the MM2.
Intermediate B
The most stable structures are those that have both bonds for the acetyl group on the same face of the molecule, with most of the difference to the MM2 energy coming from the lower bending energy when both bonds are on the same face. The torsion also plays a smaller effect opposing the difference in bending energy as the forms where there is one bond on each face have a lower torsional strain than those both on the same face as the twist that is required to put one bond on each face increases the bond angle and so decreases the strain.
The overall lowest energy form is the one where both bonds are formed on the bottom face and is stabilised by participation of the terminal OMe group in a similar way as the acetyl down, carbonyl up structure for the intermediate A was. For this form the MM2 calculation is very different to the PM6 with the Oring-C=O bond angle being 113° for the MM2 calculation and 104° for the PM6 calculation. This change in bond angle is mainly due to the terminal OMe group moving around to interact with the oxenium ion, twisting the ring so that the acetyl is forced into an axial position. The C=O also lengthens, changing from 1.2187Å for MM2 to 1.2877Å. The O-C=O bond angle in the acetyl widens from 112° to 114° corresponding to decrease in sp2 character of the bond, however the decrease is not as significant as for intermediate A. There is also a general decrease in bond length for the PM6 method.
Mini Project
Taxol Intermediate
Optimisation
An intermediate in the synthesis of taxol with the carbonyl pointing upwards is shown in (structure 17). This structure was minimised using the MM2 method:
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 376: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 5.4233 Bend: 20.8592 Stretch-Bend: 0.8130 Torsion: 21.8004 Non-1,4 VDW: 2.0064 1,4 VDW: 16.5747 Dipole/Dipole: -2.2468 Total Energy: 65.2303 kcal/mol Calculation completed ------------------------------------
The structure was then submitted to optimisation using the B3LYP method with a 6-31G(d,p) basis set using a benzene solvent environment (keywords: # RB3LYP/6-31G(d,p) Opt SCRF=(CPCM,Solvent=benzene)). The optimised files can be found at DOI:10042/24347 .
| File Name | AHall_taxol_opt |
| File Name | AHall_taxol_nmr |
| File Type | .fch |
| Calculation Type | SP |
| Calculation Method | RMPW1PW91 |
| Basis Set | 6-31G(D,P) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy | -1651.64031896 a.u. |
| RMS Gradient Norm | 0.00000000 a.u. |
| Imaginary Freq | |
| Dipole Moment | 4.1990 Debye |
| Point Group | |
| Job cpu time: | 0 days 16 hours 43 minutes 36.3 seconds. |
Item Value Threshold Converged?
Maximum Force 0.000015 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.001165 0.001800 YES
RMS Displacement 0.000206 0.001200 YES
Predicted change in Energy=-2.388588D-08
Optimization completed.
-- Stationary point found.
NMR

To determine the NMR spectrum another calculation was run using the keyword # mpw1pw91/6-31G(d,p) NMR SCRF=(CPCM,Solvent=Chloroform). The output files can be found at DOI:10042/24348 .
| Calculated Shift (ppm) | Degeneracy | Atoms | Literature Shift (ppm)[4] |
|---|---|---|---|
| 217.5580700513 | 1.0000 | 7 | 218.79 |
| 146.8718778670 | 1.0000 | 14 | 144.63 |
| 125.4320810175 | 1.0000 | 9 | 125.33 |
| 87.8671952225 | 1.0000 | 3 | 72.88 |
| 59.8503147090 | 1.0000 | 2 | - |
| 57.1496002243 | 1.0000 | 1 | 56.19 |
| 52.0271495959 | 1.0000 | 11 | 52.52 |
| 51.3486023828 | 1.0000 | 15 | 48.50 |
| 47.4060036639 | 1.0000 | 8 | 46.80 |
| 45.8216003306 | 1.0000 | 20 | 45.76 |
| 41.9817445965 | 1.0000 | 4 | 39.80 |
| 40.1770004732 | 1.0000 | 21 | 38.81 |
| 35.5407984308 | 1.0000 | 10 | 35.85 |
| 31.1468115922 | 1.0000 | 12 | 32.66 |
| 29.5817067271 | 1.0000 | 23 | 28.79 |
| 29.1419948542 | 1.0000 | 6 | 28.29 |
| 27.0785041769 | 1.0000 | 13 | 26.88 |
| 26.4206987212 | 1.0000 | 17 | 25.66 |
| 22.9794513824 | 1.0000 | 5 | 23.86 |
| 20.2062955307 | 1.0000 | 16 | 20.96 |
| - | - | - | 18.71 |
| Calculated Shift (ppm) | Degeneracy | Atoms | Literature Shift (ppm)[4] |
|---|---|---|---|
| 5.2780247271 | 1.0000 | 33 | 4.84 (1H) |
| 3.3718811860 | 1.0000 | 48 | 3.40-3.10 (m, 4H) |
| 3.2668603922 | 1.0000 | 47 | 3.40-3.10 (m, 4H) |
| 3.1403186317 | 1.0000 | 24 | 3.40-3.10 (m, 4H) |
| 3.0640977854 | 2.0000 | 50,49 | 3.40-3.10 (m, 4H) |
| 2.7414930775 | 2.0000 | 40,35 | 2.99 (1H) |
| 2.6076583133 | 1.0000 | 42 | 2.80-1.35 (series of m, 14 H) |
| 2.5108969465 | 1.0000 | 32 | 2.80-1.35 (series of m, 14 H) |
| 2.4181982911 | 3.0000 | 34,31,26 | 2.80-1.35 (series of m, 14 H) |
| 2.3189313623 | 2.0000 | 38,39 | 2.80-1.35 (series of m, 14 H) |
| 2.1732250874 | 1.0000 | 36 | 2.80-1.35 (series of m, 14 H) |
| 2.0947238584 | 1.0000 | 30 | 2.80-1.35 (series of m, 14 H) |
| 1.9953348035 | 1.0000 | 25 | 2.80-1.35 (series of m, 14 H) |
| 1.9132288129 | 1.0000 | 28 | 2.80-1.35 (series of m, 14 H) |
| 1.7862770702 | 1.0000 | 51 | 2.80-1.35 (series of m, 14 H) |
| 1.6607775097 | 2.0000 | 27,37 | 2.80-1.35 (series of m, 14 H) |
| 1.5941869755 | 1.0000 | 45 | 1.38 (3H) |
| 1.5163310642 | 1.0000 | 29 | 1.38 (3H) |
| 1.2297020834 | 1.0000 | 52 | 1.25 (3H) |
| 0.9538500274 | 4.0000 | 43,46,44,41 | 1.10 (3H) |
| 0.6533519579 | 1.0000 | 53 | 1.00-4.80 (m, 1H) |
The 13C NMR data generally matches the literature data relatively well, particularly for the higher shifts. There are a few deviations from the literature data, in particular the literature peak at 72.88ppm is calculated to be at a significantly higher shift (88ppm). This carbon is the one which is bonding to both sulfur atoms, and so the difference in chemical shift is likely to be due to a difference in conformation at this point in the real molecule to the calculated one. The rest of the shifts are within 5% of the literature shift and so indicate that this calculation was successful. The small differences in chemical shift are probably due to the structure not quite being in its optimal geometry due to approximations made by the calculation method or the location of a minima on the potential energy surface of slightly higher energy. As the molecule is not entirely rigid it is very hard to find the absolute minimum as there are many bonds which can be in slightly different meta-stable orientations.
The 1H NMR data is not as good a fit as the 13C data, although it is difficult to tell much information about the peaks as the literature assignments list ranges of lots of peaks. One particular problem is that the integrals of the peaks do not match up well with the calculated integrals, which may be due to calculation error or incomplete minimisation of the diene molecule.
Tetrazoles
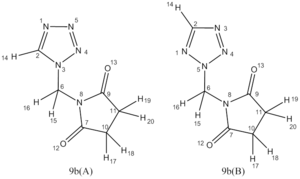
N-(R-Aminoalkyl)tetrazoles exist in two different tautomeric forms, depending on whether the R group is attached to a nitrogen adjacent to one carbon and one nitrogen or to a nitrogen adjacent to two more nitrogen atoms. The two different tautomeric forms are labled 9b(A) and 9b(B) in the diagram to the right. A practical NMR study has been carried out to determine which isomer is favoured in the equilibrium for a range of different 'R' substituents.[5] These tetrazoles are particuarly suited to NMR study, as they are virtually indistinguishable by IR or mass spectrometry due to the similarity in structures. 13C, 1H and 15N are all recorded by Katritzky et al. for these molecules and give very distinct peaks indicative of each tautomer.
In particular the key difference in NMR spectrum are expected to occur for the two different nitrogen atoms that the R group may bond to, as well as neighboring nuclei which would be expected to experience secondary effects due to changes in local electron density due to the differences in bonding.
Optimisation
Optimisation was carried out first using the MM2 method, followed by a B3LYP/6-31G(d,p) minimisation. Output files can be found at DOI:10042/24368 and DOI:10042/24369 . 9b(A)
------------MM2 Minimization------------ Pi System: 3 2 1 4 5 Warning: Some parameters are guessed (Quality = 1). Iteration 1083: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 0.5376 Bend: 20.9633 Stretch-Bend: -0.1933 Torsion: 2.7197 Non-1,4 VDW: -2.0079 1,4 VDW: 3.7070 Dipole/Dipole: -4.3613 Total Energy: 21.3652 kcal/mol Calculation completed ------------------------------------
| File Name | AHall_9bA_opt |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -657.06420777 a.u. |
| RMS Gradient Norm | 0.00001334 a.u. |
| Imaginary Freq | |
| Dipole Moment | 8.6418 Debye |
| Point Group | C1 |
| Job cpu time: | 0 days 2 hours 1 minutes 30.8 seconds. |
Item Value Threshold Converged?
Maximum Force 0.000019 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.001795 0.001800 YES
RMS Displacement 0.000373 0.001200 YES
Predicted change in Energy=-1.837819D-08
Optimization completed.
-- Stationary point found.
9b(B)
------------MM2 Minimization------------ Pi System: 3 2 1 5 Warning: Some parameters are guessed (Quality = 1). Iteration 575: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 0.5405 Bend: 13.6522 Stretch-Bend: -0.1083 Torsion: 3.1719 Non-1,4 VDW: -2.2241 1,4 VDW: 4.4664 Dipole/Dipole: -0.4654 Total Energy: 19.0333 kcal/mol Calculation completed ------------------------------------
| File Name | AHall_9bB_opt |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -657.06389878 a.u. |
| RMS Gradient Norm | 0.00001430 a.u. |
| Imaginary Freq | |
| Dipole Moment | 5.1372 Debye |
| Point Group | C1 |
| Job cpu time: | 0 days 2 hours 14 minutes 38.6 seconds. |
Item Value Threshold Converged?
Maximum Force 0.000046 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.001280 0.001800 YES
RMS Displacement 0.000282 0.001200 YES
Predicted change in Energy=-1.941047D-08
Optimization completed.
-- Stationary point found.
NMR
NMR spectra were calculated for both molecules using the mpw1pw91/6-31G(d,p) method using DMSO as the solvent (solvation method=CPCM). As there is no preloaded TMS standard in GaussView for this method/solvation, a new TMS standard was created by optimisation and calculation of the TMS NMR spectrum using the above method/solvation. The TMS NMR data was then used to create a new standard for use in NMR comparison. The files used in the NMR calculations can be found at DOI:10042/24371 and DOI:10042/24372 .

| Atoms | 9bA | 9bB | ||
|---|---|---|---|---|
| Calc. Shift (ppm) | Lit.[5] Shift (ppm) | Calc. Shift (ppm) | Lit. Shift (ppm) | |
| 2 | 143.1514656986 | 146.4 | 150.9620623384 | 155.3 |
| 6 | 50.6848307318 | 48.9 | 54.5947432372 | 53.4 |
| 7, 9 | 175.2891916085, 172.9995132117 | 178.4 | 173.7423859277 | 178.0 |
| 10, 11 | 30.0943563558, 30.6640691616 | 30.0 | 30.0921938184, 30.3947566515 | 29.9 |
From the 13C NMR data it can be seen that for carbon 2 (inside the ring) and carbon 6 (bonded to the tetrazole ring) the chemical shifts for the two tautomers are very different, with the carbon becoming more deshielded for the 'B' tautomer as the carbon is in a region of higher electron density. Carbon 6 is also deshielded in tautomer B as it is bonded to a nitrogen which is more electron rich than in tautomer A as it has two neighboring nitrogen atoms to donate electron density. As the other carbon atoms are quite far from the tetrazole ring they are not significantly affected by the change in ring bonding position. The calculated chemical shifts are a reasonable match for the literature values with <5% deviation in most cases. The deviations which are observed are most likely due to approximations taken in calculation steps or slight imperfections in the structure.


| Atoms | 9bA | 9bB | ||
|---|---|---|---|---|
| Calc. Shift (ppm) | Lit.[5] Shift (ppm) | Calc. Shift (ppm) | Lit. Shift (ppm) | |
| 14 | 9.2846486703 | 9.42 | 8.8256581033 | 9.01 |
| 15, 16 | 6.2180339081, 5.7191761824 | 6.02 | 6.2050359626 | 6.20 |
| 17, 18, 19, 20 | 2.7130992367, 2.6257819177, 2.6257819177, 2.7130992367 | 2.69 | 2.6818353934, 2.5593985668, 2.6818353934, 2.6818353934 | 2.74 |
The 1H NMR data also shows that the protons in close proximity to the ring are more strongly affected by the change in bonding position. For proton 14 (on the tetrazole ring) the change is the opposite to that observed for carbon, with the proton becoming more shielded for tautomer B. The other two protons that are close to the tetrazole ring (15 and 16) are deshielded in tautomer B which implies that the deshielding is related to a ring current which affects protons differently depending on their distance from the ring. The calculated chemical shifts are a good match for the literature values with less than 0.2ppm difference in most cases.


| 9bA | 9bB | ||||
|---|---|---|---|---|---|
| Atom | Calc. Shift (ppm) | Lit.[5] Shift (ppm) | Atom | Calc. Shift (ppm) | Lit. Shift (ppm) |
| 1 | 335.1348192840 | 395.0 | 3 | 310.2839000000 | not measured |
| 3 | 248.1045641560 | 239.3 | 1 | 337.6268000000 | 383.5 |
| 4 | 372.5110029849 | 370.0 | 5 | 388.8404000000 | 307.9 |
| 5 | 397.1375831567 | not measured | 4 | 293.3246000000 | 284.1 |
| 8 | 192.9850592954 | 180.4 | 8 | 191.4648000000 | 180.0 |
NB. The atoms are labeled differently on each molecule, each row indicates the same atom in each structure.
The 15N NMR(reference=NH3) shows the biggest difference of all of the NMR spectra, and some of the literature assignments do not match the calculated peaks. The literature assigns the peak at 395.0ppm to atom 1 in tautomer A, however when the calculated shifts are considered this peak would appear to be more similar to that for atom 5, so it is possible that this peak was assigned incorrectly. In tautomer B a similar anomaly is noticed as the literature peak at 307.9ppm is assigned to atom 4, whereas the calculations imply that this would be better assigned to atom 1. The peak at 383.5ppm is also much closer to the calculated peak for atom 4 than for atom 3 as it is assigned.
After these corrections are accounted for the fit between the calculated and the literature shifts is not too bad, however there are still some significant differences, for example for atom 4 in the B tautomer where the literature value is 284, but the calculated value is 293ppm. This may be due to calculation inaccuracies.
There are big differences between the chemical shifts for the same atoms in each tautomer, for example atom 3 in the A tautomer has a shift of 239ppm, however the corresponding atom (1) in the B tautomer has a shift of 383ppm. This large change is because the atom is bonding to the R group in tautomer A, whereas in tautomer B the atom is no longer attached to the R group, causing a large change in environment.
Pinene
The techniques used for the calculation of the tetrazole NMR can also be applied to many other molecules. Pinene was also calculated, however as this is often used as a standard in the development of many of the calculation methods this molecule was not necessarily an ideal choice for an original study and so is only included as additional material.
Introduction
Pinene is a bicyclic hydrocarbon from the monoterpene class of compounds which is found in pine needles and is commonly used as a starting material in the synthesis of perfumes. Pinene has two structural isomers (α and β) which depend on the location of the double bond in the molecule. Each of these structural isomers has two enantiomers, however unless chiral shift agents are used these will not cause any difference to the NMR spectra.
As pinene is an abundant natural product there are relatively few papers detailing its synthesis, however some do exist [6]. As pinene is most commonly extracted from natural sources, which contain both α and β isomers it is important to be able to identify which isomer is in each fraction after distillation. NMR analysis would help determine which isomer is present (however cannot distinguish between the different enantiomers), however in practise the physical properties (eg. boiling point) are the main method of identifying which isomer is present.
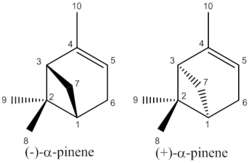 |

|
| α-pinene | β-pinene |
|---|
Optimisation
The α and β forms of pinene were optimised using the MM2 method:
α-pinene
------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 220: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.7991 Bend: 21.2439 Stretch-Bend: -1.1787 Torsion: 10.6087 Non-1,4 VDW: -0.4309 1,4 VDW: 6.4995 Dipole/Dipole: 0.1965 Total Energy: 38.7381 kcal/mol Calculation completed ------------------------------------
β-pinene
------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 248: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.7876 Bend: 20.8238 Stretch-Bend: -1.0284 Torsion: 15.3586 Non-1,4 VDW: -0.3028 1,4 VDW: 6.8837 Dipole/Dipole: 0.0000 Total Energy: 43.5225 kcal/mol Calculation completed ------------------------------------
Further optimisation was carried out using the RB3lYP method with a 6-31G(d,p) basis set, specifying a chloroform solvent environment using the CPCM method (see optimised files at DOI:10042/24202 and DOI:10042/24203 ).
α-pinene
| File Name | AHall_pin_alpha_OPT |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -390.68327081 a.u. |
| RMS Gradient Norm | 0.00002564 a.u. |
| Imaginary Freq | |
| Dipole Moment | 0.2212 Debye |
| Point Group | C1 |
| Job cpu time: | 0 days 0 hours 49 minutes 41.9 seconds. |
Item Value Threshold Converged?
Maximum Force 0.000043 0.000450 YES
RMS Force 0.000013 0.000300 YES
Maximum Displacement 0.001355 0.001800 YES
RMS Displacement 0.000316 0.001200 YES
Predicted change in Energy=-1.127783D-07
Optimization completed.
-- Stationary point found.
β-pinene
| File Name | AHall_pin_beta_OPT |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -390.67869132 a.u. |
| RMS Gradient Norm | 0.00001079 a.u. |
| Imaginary Freq | |
| Dipole Moment | 0.8624 Debye |
| Point Group | C1 |
| Job cpu time: | 0 days 0 hours 57 minutes 14.3 seconds. |
Item Value Threshold Converged?
Maximum Force 0.000018 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.001663 0.001800 YES
RMS Displacement 0.000269 0.001200 YES
Predicted change in Energy=-1.854955D-08
Optimization completed.
-- Stationary point found.
13C NMR
Using the optimised checkpoint files of the two pinene molecules the NMR spectrum was calculated using the mpw1pw91/6-31G(d,p) method with solvent effects calculated for chloroform using the CPCM method (see files at DOI:10042/24207 and DOI:10042/24206 ).


| Carbon Number | Calculated shift/δ | Degeneracy | Literature Shift/δ[7] | Literature Assignment |
|---|---|---|---|---|
| 1 | 42.4311159099 | 1.0000 | ||
| 2 | 42.5373383383 | 1.0000 | ||
| 3 | 47.9318176510 | 1.0000 | 47.8 | 3 |
| 4 | 144.8864470892 | 1.0000 | 145.0 | 4 |
| 5 | 117.2934306007 | 1.0000 | 116.6 | 5 |
| 6 | 33.6007706627 | 1.0000 | ||
| 7 | 34.0539668434 | 1.0000 | ||
| 8 | 26.6134661376 | 1.0000 | 27.0 | 9 |
| 9 | 21.8189300694 | 1.0000 | 21.4 | 10 |
| 10 | 24.5063068649 | 1.0000 | 23.5 | 8 |
| Carbon Number | Calculated shift/δ | Degeneracy | Literature Shift/δ[7] | Literature Assignment |
|---|---|---|---|---|
| 1 | 42.0564239403 | 1.0000 | ||
| 2 | 44.9292311807 | 1.0000 | ||
| 3 | 52.6462739781 | 1.0000 | 52.9 | 3 |
| 4 | 150.5374707994 | 1.0000 | 152.7 | 4 |
| 5 | 26.8928060552 | 1.0000 | ||
| 6 | 26.1208142537 | 1.0000 | ||
| 7 | 28.1310383116 | 1.0000 | 27.6 | 7 |
| 8 | 26.3314231813 | 1.0000 | 26.5 | 9 |
| 9 | 22.8816731987 | 1.0000 | 22.2 | 8 |
| 10 | 106.0386915199 | 1.0000 | 106.8 | 10 |
References
- ↑ Braddock, C. Alkanes, Alkenes and Alkynes, Lecture 3 1st year lecture course, Imperial College London
- ↑ Wilhelm F. Maier and Paul von Ragué Schleyer; J. Am. Chem. Soc. 1981, 103, pp.1891-1900 DOI:10.1021/ja00398a003
- ↑ Alan B. McEwent and Paul von Ragué Schleyer; J. Am. Chem. Soc. 1986, 108, pp.3951-3960 DOI:10.1021/ja00274a016
- ↑ 4.0 4.1 Leo A. Paquette, Neil A. Pegg, Dana Toops, George D. Maynard, and Robin D. Rogers; J. Am. Chem. Soc. 1990, 112, pp.211-283 DOI:0.1021/ja00157a043
- ↑ 5.0 5.1 5.2 5.3 Katritzky, Alan R.; El-Gendy, Bahaa El-Dien M.; Draghici, Bogdan; Hall, C. Dennis and Steel, Peter J. J. Org. Chem. Vol. 75, No. 19, 2010 pp.6468-6476 DOI:10.1021/jo101195z
- ↑ M. T. Thomas and A. G. Fallis, J. Am. Chem. Soc., 1976, 98, 1227-1231. DOI:10.1021/ja00421a029
- ↑ 7.0 7.1 E. D. Skakovskii, S. A. Lamotkin, S. I. Shpak, L. Y. Tychinskaya, O. A. Gaidukevich, and A. I. Lamotkin, Journal of Applied Spectroscopy, 2006, 73, 275-279 LA - English. DOI:10.1007/s10812-006-0068-2
