Bonding and Molecular Orbitals in Main Group Compounds

Amh110 15:12, 18 February 2013 (UTC)

Optimisation of BH₃

Using 3-21G basis set

BH₃ was optimised using the B3LYP method with a 3-21G basis set. The optimised .log file can be found here.

B-H bond length = 1.19349Å (lit.^[1] 1.1900Å)
H-B-H bond angle = 120.000°
Total energy = -26.46226338 au (-69476.7 kJ/mol)

3-21G optimisation
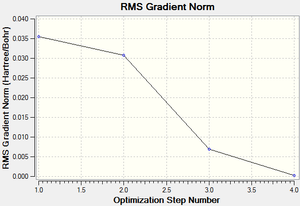
File Name	BH3_opt
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Charge	0
Spin	Singlet
E(RB3LYP)	-26.46226338 a.u.
RMS Gradient Norm	0.00020672 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	D3H
Job cpu time:	0 days 0 hours 0 minutes 20.0 seconds.

 Item               Value     Threshold  Converged?
 Maximum Force            0.000413     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.
    -- Stationary point found.

Using 6-31G(d,p) basis set

Using the output from the previous optimisation a further optimisation was performed using the B3LYP method with a 6-31G(d,p) basis set. The output .log file can be found here.

B-H bond length = 1.19349Å
H-B-H bond angle = 120.000°
Total energy = -26.61722301 au (-69883.5 kJ/mol)

6-31G(d,p) optimisation
File Name	BH3_OPT_631g_dp
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31+G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-26.61722301 a.u.
RMS Gradient Norm	0.00014139 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	D3H
Job cpu time:	0 days 0 hours 0 minutes 10.0 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000283     0.000450     YES
 RMS     Force            0.000185     0.000300     YES
 Maximum Displacement     0.001125     0.001800     YES
 RMS     Displacement     0.000736     0.001200     YES
 Predicted change in Energy=-4.770182D-07
 Optimization completed.
    -- Stationary point found.

Pseudo-Potentials

Optimisation of TlBr₃

The geometry of TlBr₃ was optimised using a B3LYP method with a medium level basis set; LanL2DZ. The geometry of the TlBr₃ was constrained so that only solutions with a D_3h point group were calculated. A link to the optimised .log file can be found at DOI:10042/23345 .

Tl-Br bond length = 2.65095 Å (lit.^[1] 2.6182Å)
Br-B-Br bond angle = 120.000°
Total energy = -91.21812851 au

TlBr₃ optimisation
File Name	TlBr3_opt_LanL2DZ
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-91.21812851 a.u.
RMS Gradient Norm	0.00000090 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	D3H
Job cpu time:	0 days 0 hours 0 minutes 29.3 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000014     0.001200     YES
 Predicted change in Energy=-6.084070D-11
 Optimization completed.
    -- Stationary point found.

Optimisation of BBr₃

Using the output from the 6-31G(d,p) optimised BH₃ molecule, the hydrogen atoms were changed for bromine atoms. The molecule was then optimised using a 6-31G(d,p) basis set for the boron atom and a LanL2DZ basis set for the bromines. A link to the optimised .log file can be found at DOI:10042/23346 .

B-Br bond length = 1.93396 Å (lit.^[1] 1.893Å)
Br-B-Br bond angle = 120.000°
Total energy = -64.43645296 au

BBr₃ optimisation
File Name	BBr3_OPT_GEN
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	GEN
Charge	0
Spin	Singlet
E(RB3LYP)	-64.43645296 a.u.
RMS Gradient Norm	0.00000382 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	D3H
Job cpu time:	0 days 0 hours 0 minutes 23.9 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.027020D-10
 Optimization completed.
    -- Stationary point found.

Comparison of Bond lengths

Optimised bond lengths
Molecule	Bond Length/Å
BH₃	1.19349
BBr₃	1.93396
TlBr₃	2.65095

NB. When BH₃ is optimised with starting bond lengths 1.5Å the optimised bond length is 1.19349Å. If the structure is optimised starting from default bond length (1Å) then the optimised length is 1.19231Å.

The bond length for BH₃ is approximately 0.74Å shorter than the bond length for BBr₃. This can be explained by considering the differences in size of the ligands, as bromine is a much larger atom than hydrogen and so the distance between the boron and bromine nuclei will be much greater than the distance between the boron and hydrogen nuclei. As the bromine has very diffuse orbitals when compared to the hydrogen, interaction of the bromine and boron atoms will be weaker, also leading to a longer bond length. Both bromine and hydrogen atoms are one electron short of a full valence shell and so form a single covalent bond to boron, however the atoms are of very different sizes and so the bonds have different properties.

Changing the central atom to thallium also causes a large increase in bond length. Thallium is a much larger atom than boron and so again will cause a lengthening of the bond, as the valence electrons are much further from the nucleus and so the nuclei must be further apart to bond. There is a large size difference between thallium and bromine atoms, so the orbitals are much more diffuse for thallium than bromine, causing poorer interaction.

Gaussian shows bonds whenever two atoms are within a set distance which is predetermined from known bond lengths. In some cases Gaussian will not show a bond where one is expected to exist, as the atoms forming the bond are too far apart. This does not necessarily mean that there is no bonding interaction between the atoms as the visual representation supplied by the computer is only a model to illustrate the relative positions of the atoms, and does not show how the electrons are interacting in the molecule.

The concept of a physical bond is an inaccurate way of describing the interactions between atoms, which are better represented by showing the electronic interactions with molecular orbitals, however the concept of a bond is a useful approximation to simplify interactions within molecules. A covalent bond is where two atoms are held together by the presence of electron density between the atoms.

Frequency Calculations

BH₃

Optimisation

A molecule of BH₃ was optimised using the B3LYP method and the basis set 3-21G followed by a further optimisation using the basis set 6-31G(d,p). The optimised .log file can be found here.

B-H bond length = 1.19231 Å (lit.^[1] 1.1900Å)
H-B-H bond angle = 120°
Energy = -26.61532363 au.

BH3 re-optimised
File Name	BH3_opt_6-31Gdp_2
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-26.61532363 a.u.
RMS Gradient Norm	0.00000475 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	D3H
Job cpu time:	0 days 0 hours 0 minutes 11.0 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000009     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000038     0.001800     YES
 RMS     Displacement     0.000025     0.001200     YES
 Predicted change in Energy=-5.342736D-10
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

Frequency analysis was performed using the B3LYP method and the basis set 6-31G(b,p). The energy after frequency analysis was the same as for the geometry optimisation. The .log file can be found here.

BH3 freguency
File Name	AHall_bh3_freq_2
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-26.61532363 a.u.
RMS Gradient Norm	0.00000477 a.u.
Imaginary Freq	0
Dipole Moment	0.0000 Debye
Point Group	D3H
Job cpu time:	0 days 0 hours 0 minutes 14.0 seconds.

 Item               Value     Threshold  Converged?
 Maximum Force            0.000010     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000038     0.001800     YES
 RMS     Displacement     0.000019     0.001200     YES
 Predicted change in Energy=-5.368808D-10
 Optimization completed.
    -- Stationary point found.

Low frequencies ---   -3.5991   -1.1355   -0.0054    1.3745    9.7046    9.7707
 Low frequencies --- 1162.9825 1213.1733 1213.1760
 Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
 activities (A**4/AMU), depolarization ratios for plane and unpolarized
 incident light, reduced masses (AMU), force constants (mDyne/A),
 and normal coordinates:
                     1                      2                      3
                    A2"                    E'                     E'
 Frequencies --  1162.9825              1213.1733              1213.1760
 Red. masses --     1.2531                 1.1072                 1.1072
 Frc consts  --     0.9986                 0.9601                 0.9601
 IR Inten    --    92.5497                14.0545                14.0581
  Atom  AN      X      Y      Z        X      Y      Z        X      Y      Z
     1   5     0.00   0.00   0.16     0.00   0.10   0.00    -0.10   0.00   0.00
     2   1     0.00   0.00  -0.57     0.00   0.08   0.00     0.81   0.00   0.00
     3   1     0.00   0.00  -0.57     0.39  -0.59   0.00     0.14  -0.39   0.00
     4   1     0.00   0.00  -0.57    -0.39  -0.59   0.00     0.14   0.39   0.00
                     4                      5                      6
                    A1'                    E'                     E'
 Frequencies --  2582.3247              2715.4994              2715.5006
 Red. masses --     1.0078                 1.1273                 1.1273
 Frc consts  --     3.9597                 4.8979                 4.8979
 IR Inten    --     0.0000               126.3285               126.3189
  Atom  AN      X      Y      Z        X      Y      Z        X      Y      Z
     1   5     0.00   0.00   0.00     0.11   0.00   0.00     0.00   0.11   0.00
     2   1     0.00  -0.58   0.00     0.02   0.00   0.00     0.00  -0.81   0.00
     3   1     0.50   0.29   0.00    -0.60  -0.36   0.00    -0.36  -0.19   0.00
     4   1    -0.50   0.29   0.00    -0.60   0.36   0.00     0.36  -0.19   0.00

Table of Vibrations
No.	Symmetry	Frequency/cm^-1	Intensity	Description
1	A2"	1162.98	92.5497	All hydrogen atoms bend out of plane in a concerted manner. Small motion of boron atom opposing motion of hydrogens.
2	E'	1213.17	14.0545	Two hydrogen atoms bend in plane in a scissoring motion. Small motion of boron atom opposing motion of hydrogens.
3	E'	1213.18	14.0581	The entire molecule rocks (small side-to-side motion of boron) with one hydrogen atom moving horizontally in a sort of scissoring motion with both other hydrogens.
4	A1'	2582.32	0.0000	All B-H bonds stretch symmetrically in a concerted motion. Boron atom remains stationary.
5	E'	2715.50	126.3285	Asymmetric stretching of two B-H bonds. Small motion of Boron atom away from stretching bond.
6	E'	2715.50	126.3189	Two hydrogens stretch symmetrically with the third also stretching in a concerted manner, however with opposing phase. Small motion of boron atom opposing motion of symmetric stretching hydrogens.

The second and third and the fifth and sixth vibrations are very close in frequency, and so are overlapped on the spectrum leading to only three peaks being visible on the spectrum.

TlBr₃

Frequency analysis was carried out on TlBr₃ using the previously optimised .log file as the input. The output .log file can be found at: DOI:10042/23395 .

TlBr₃ frequency
File Name	AHall_TlBr3_freq
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-91.21812851 a.u.
RMS Gradient Norm	0.00000088 a.u.
Imaginary Freq	0
Dipole Moment	0.0000 Debye
Point Group	D3H
Job cpu time:	0 days 0 hours 0 minutes 22.2 seconds.

        Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000011     0.001200     YES

 Low frequencies ---   -3.4213   -0.0026   -0.0004    0.0015    3.9367    3.9367
 Low frequencies ---   46.4289   46.4292   52.1449
 Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
 activities (A**4/AMU), depolarization ratios for plane and unpolarized
 incident light, reduced masses (AMU), force constants (mDyne/A),
 and normal coordinates:
                     1                      2                      3
                    E'                     E'                     A2"
 Frequencies --    46.4289                46.4292                52.1449
 Red. masses --    88.4613                88.4613               117.7209
 Frc consts  --     0.1124                 0.1124                 0.1886
 IR Inten    --     3.6867                 3.6867                 5.8466
  Atom  AN      X      Y      Z        X      Y      Z        X      Y      Z
     1  81     0.00   0.28   0.00    -0.28   0.00   0.00     0.00   0.00   0.55
     2  35     0.00   0.26   0.00     0.74   0.00   0.00     0.00   0.00  -0.48
     3  35     0.43  -0.49   0.00    -0.01  -0.43   0.00     0.00   0.00  -0.48
     4  35    -0.43  -0.49   0.00    -0.01   0.43   0.00     0.00   0.00  -0.48
                     4                      5                      6
                    A1'                    E'                     E'
 Frequencies --   165.2685               210.6948               210.6948
 Red. masses --    78.9183               101.4032               101.4032
 Frc consts  --     1.2700                 2.6522                 2.6522
 IR Inten    --     0.0000                25.4830                25.4797
  Atom  AN      X      Y      Z        X      Y      Z        X      Y      Z
     1  81     0.00   0.00   0.00     0.42   0.00   0.00     0.00   0.42   0.00
     2  35     0.00  -0.58   0.00     0.01   0.00   0.00     0.00  -0.74   0.00
     3  35     0.50   0.29   0.00    -0.55  -0.32   0.00    -0.32  -0.18   0.00
     4  35    -0.50   0.29   0.00    -0.55   0.32   0.00     0.32  -0.18   0.00

The lowest 'real' mode is 46.4289cm^-1, approximately 10 times greater than the highest 'zero' frequency mode.

Table of Vibrations for TlBr₃
No.	Symmetry	Frequency/cm^-1	Intensity	Description
1	E'	46.43	3.6867	Two of the bromine atoms move in a scissoring motion. The thallium and remaining bromine atom move in the opposite direction to the scissoring motion in a concerted manner.
2	E'	46.43	3.6867	One bromine atom rocks in the plane of the molecule. The rest of the molecule bends in the opposite direction.
3	A2"	52.14	5.8466	Out of plane bending of entire molecule. The thalium atom moves in the opposite direction to the bromine atoms with a similar magnitude.
4	A1'	165.27	0.0000	Symmetrical stretching of Tl-Br bonds in the plane of the molecule.
5	E'	210.69	25.4830	Asymmetric stretching of two Tl-Br bonds. Thallium atom moves significantly towards the contracting Tl-Br bond. The third bromine atom remains stationary.
6	E'	210.69	25.4797	Asymmetric stretching of entire molecule. Two bonds lengthen as the other bond contracts, and the thallium atom moves significantly towards the contracting Tl-Br bond(s).

Comparison

IR stretching frequencies of BH₃ and TlBr₃.
Number	BH₃		TlBr₃
Number	Frequency /cm^-1	Symmetry	Frequency /cm^-1	Symmetry
1	1162.98	A2"	46.43	E'
2	1213.17	E'	46.43	E'
3	1213.18	E'	52.14	A2"
4	2582.32	A1'	165.27	A1'
5	2715.50	E'	210.69	E'
6	2715.50	E'	210.69	E'

There is a large difference in the stretching frequencies for BH₃ and TlBr₃, which reflects the difference in bond strength. As the BH₃ has higher frequency vibrations the energy needed to cause the vibrations is higher, indicating a stronger bond. This increased bond strength results in the B-H bond being much shorter than the Tl-Br bond.

For TlBr₃ the out-of-plane bending mode is the third vibration observed, whereas for BH₃ this mode is the first observed. As the energies of the modes are fairly similar, the change required to cause this reordering does not need to be very large.

Both spectra show a single peak at higher frequencies and two peaks close together at lower frequencies, with the single peak being of much higher intensity than the two lower peaks. The separation between the peaks is much greater for the BH₃ than for the TlBr₃. The vibrations can be divided into two sets; vibrations 1-3 which have lower frequency, and vibrations 4-6 which have higher frequency. The first set of vibrations are due to bending of the bonds, whereas the second set are due to bond stretching. As it takes more energy to stretch a bond than to bend it, the second set of vibrations are at higher frequencies.

It is important to use the same method and basis set for optimisation and frequency analysis calculations as otherwise the results will be incorrect due to differences in the optimised structure using different basis sets.

Frequency analysis is carried out to check that the optimisation has reached a minimum, as if the optimisation is not complete then the low frequencies will be large compared to the 'real' frequencies, and there is a chance that some of the 'real' frequencies will be negative, which is impossible.

The low frequencies represent the motion of the centre of mass of the molecule, and are represented by the '-6' part of the 3N-6 vibrational modes for a molecule with 'N' atoms.

MOs

BH₃

The checkpoint file (.chk) from the optimised BH₃ molecule was submitted to Energy calculation to calculate the MOs. The output checkpoint file can be found at: DOI:10042/23403 .

BH3 MOs
File Name	AHall_bh3_MOs
File Type	.fch
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	6-31G(D,P)
Charge	0
Spin	Singlet
Total Energy	-26.61532363 a.u.
RMS Gradient Norm	0.00000000 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group

MO	LCAO	Calculated	Comments
1a'₁			Not shown on MO diagram as the energy is too low.
2a'₁			Larger contribution towards LCAO from H₃ fragment due to closer energy.
1e'₁
1a"₂			Non-bonding.
3a'₁			Larger contribution towards LCAO from B fragment due to closer energy.
2e'₁			Absolute ordering of 3a'₁ and 2e'₁ is hard to predict as the energy levels are relatively close.

There is a close relationship between the LCAO predicted orbitals and the calculated MOs. The calculated MOs show what happens when the combined atomic orbitals mix producing orbitals which are delocalised over multiple atoms. Some of the anti-bonding MOs (particularly 2e'1) have lobes which are bent away from the shape predicted by LCAO due to repulsion with other lobes.

This implies that MO theory is a good representation of the position of the electrons in the molecules, as it matches well to the predicted orbitals from LCAO. The calculated MOs are better than the LCAO orbitals as they show how the orbitals mix to give bonding and anti-bonding orbitals and so can help with theory of how the bonding in the molecule works.

NBO Analysis

NH₃

Optimisation

A molecule of NH₃ was optimised using the B3LYP method with a 6-31G(d,p) basis set. The .log file can be found here.

NH3 optimisation
File Name	NH3_opt
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-56.55776856 a.u.
RMS Gradient Norm	0.00000885 a.u.
Imaginary Freq
Dipole Moment	1.8464 Debye
Point Group	C1
Job cpu time:	0 days 0 hours 0 minutes 25.0 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000024     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000079     0.001800     YES
 RMS     Displacement     0.000053     0.001200     YES
 Predicted change in Energy=-1.629732D-09
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The optimised NH₃ .log file was submitted to frequency analysis. The output .log file can be found here.

Low frequencies ---  -30.7295    0.0008    0.0014    0.0016   20.1705   28.2664
 Low frequencies --- 1089.5535 1694.1244 1694.1856
 Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
 activities (A**4/AMU), depolarization ratios for plane and unpolarized
 incident light, reduced masses (AMU), force constants (mDyne/A),
 and normal coordinates:
                     1                      2                      3
                     A                      A                      A
 Frequencies --  1089.5535              1694.1244              1694.1856
 Red. masses --     1.1800                 1.0644                 1.0644
 Frc consts  --     0.8253                 1.8000                 1.8001
 IR Inten    --   145.4405                13.5558                13.5560
  Atom  AN      X      Y      Z        X      Y      Z        X      Y      Z
     1   7     0.12   0.00   0.00     0.00  -0.02  -0.06     0.00   0.06  -0.02
     2   1    -0.53  -0.21   0.00    -0.07  -0.04   0.73     0.25   0.14   0.20
     3   1    -0.53   0.11   0.18     0.25  -0.24  -0.03    -0.07  -0.62   0.40
     4   1    -0.53   0.11  -0.18    -0.18   0.52   0.18    -0.18  -0.41  -0.36
                     4                      5                      6
                     A                      A                      A
 Frequencies --  3460.9818              3589.3998              3589.5230
 Red. masses --     1.0272                 1.0883                 1.0883
 Frc consts  --     7.2496                 8.2615                 8.2621
 IR Inten    --     1.0593                 0.2700                 0.2709
  Atom  AN      X      Y      Z        X      Y      Z        X      Y      Z
     1   7    -0.04   0.00   0.00     0.00  -0.04   0.07     0.00   0.07   0.04
     2   1     0.18  -0.55   0.00    -0.15   0.35   0.02     0.27  -0.66   0.01
     3   1     0.18   0.27   0.47    -0.16  -0.22  -0.34    -0.26  -0.31  -0.56
     4   1     0.18   0.27  -0.48     0.31   0.38  -0.65    -0.01   0.01   0.03

         Item               Value     Threshold  Converged?
 Maximum Force            0.000021     0.000450     YES
 RMS     Force            0.000009     0.000300     YES
 Maximum Displacement     0.000078     0.001800     YES
 RMS     Displacement     0.000039     0.001200     YES
 Predicted change in Energy=-1.611689D-09
 Optimization completed.
    -- Stationary point found.

As the low frequencies are significantly lower than the main frequencies the optimisation is complete.

Molecular Orbitals

A link to the .chk file for the energy calculation can be found at: DOI:10042/23452 .


MO 1	MO 2	MO 3	MO 4 (HOMO)	MO 5 (LUMO)	MO 6	MO 7	MO 8

NBO analysis

The charge distribution of NH₃ is indicated on the diagram to the left. The charge on nitrogen is -1.125 and the charge on hydrogen is 0.375

 Summary of Natural Population Analysis:                 
                                                         
                                       Natural Population
                Natural  -----------------------------------------------
    Atom  No    Charge         Core      Valence    Rydberg      Total
 -----------------------------------------------------------------------
      N    1   -1.12515      1.99982     6.11104    0.01429     8.12515
      H    2    0.37505      0.00000     0.62250    0.00246     0.62495
      H    3    0.37505      0.00000     0.62250    0.00246     0.62495
      H    4    0.37505      0.00000     0.62249    0.00246     0.62495
 =======================================================================
   * Total *    0.00000      1.99982     7.97852    0.02166    10.00000

       (Occupancy)   Bond orbital/ Coefficients/ Hybrids
 ---------------------------------------------------------------------------------
     1. (1.99909) BD ( 1) N   1 - H   2 
                ( 68.83%)   0.8297* N   1 s( 24.87%)p 3.02( 75.05%)d 0.00(  0.09%)
                                           -0.0001 -0.4986 -0.0059  0.0000 -0.2910
                                            0.0052  0.8155  0.0277  0.0000  0.0000
                                            0.0281  0.0000  0.0000  0.0032  0.0082
                ( 31.17%)   0.5583* H   2 s( 99.91%)p 0.00(  0.09%)
                                           -0.9996  0.0000  0.0072 -0.0289  0.0000
     2. (1.99909) BD ( 1) N   1 - H   3 
                ( 68.83%)   0.8297* N   1 s( 24.86%)p 3.02( 75.05%)d 0.00(  0.09%)
                                            0.0001  0.4986  0.0059  0.0000  0.2910
                                           -0.0052  0.4077  0.0138  0.7062  0.0240
                                            0.0140  0.0243  0.0076  0.0033  0.0031
                ( 31.17%)   0.5583* H   3 s( 99.91%)p 0.00(  0.09%)
                                            0.9996  0.0000 -0.0072 -0.0145 -0.0250
     3. (1.99909) BD ( 1) N   1 - H   4 
                ( 68.83%)   0.8297* N   1 s( 24.87%)p 3.02( 75.05%)d 0.00(  0.09%)
                                            0.0001  0.4986  0.0059  0.0000  0.2909
                                           -0.0052  0.4077  0.0138 -0.7062 -0.0239
                                            0.0140 -0.0243 -0.0076  0.0033  0.0031
                ( 31.17%)   0.5583* H   4 s( 99.91%)p 0.00(  0.09%)
                                            0.9996  0.0000 -0.0072 -0.0145  0.0250
     4. (1.99982) CR ( 1) N   1           s(100.00%)
                                            1.0000 -0.0002  0.0000  0.0000  0.0000
                                            0.0000  0.0000  0.0000  0.0000  0.0000
                                            0.0000  0.0000  0.0000  0.0000  0.0000
     5. (1.99721) LP ( 1) N   1           s( 25.38%)p 2.94( 74.52%)d 0.00(  0.10%)
                                            0.0001  0.5036 -0.0120  0.0000 -0.8618
                                            0.0505  0.0000  0.0000  0.0000  0.0000
                                            0.0000  0.0000  0.0000 -0.0269  0.0155
     6. (0.00000) RY*( 1) N   1           s( 99.98%)p 0.00(  0.02%)d 0.00(  0.00%)
     7. (0.00000) RY*( 2) N   1           s(100.00%)
     8. (0.00000) RY*( 3) N   1           s(  0.03%)p99.99( 99.97%)d 0.01(  0.00%)
     9. (0.00000) RY*( 4) N   1           s(  0.00%)p 1.00(100.00%)d 0.00(  0.00%)
    10. (0.00000) RY*( 5) N   1           s(  0.00%)p 1.00(100.00%)d 0.00(  0.00%)
    11. (0.00000) RY*( 6) N   1           s(  0.00%)p 1.00(  0.12%)d99.99( 99.88%)
    12. (0.00000) RY*( 7) N   1           s(  0.00%)p 1.00(  0.12%)d99.99( 99.88%)
    13. (0.00000) RY*( 8) N   1           s(  0.00%)p 1.00(  0.01%)d99.99( 99.99%)
    14. (0.00000) RY*( 9) N   1           s(  0.01%)p 4.42(  0.06%)d99.99( 99.92%)
    15. (0.00000) RY*(10) N   1           s(  0.00%)p 1.00(  0.03%)d99.99( 99.97%)
    16. (0.00112) RY*( 1) H   2           s( 72.77%)p 0.37( 27.23%)
                                            0.0038  0.8531  0.5218 -0.0017 -0.0001
    17. (0.00045) RY*( 2) H   2           s( 26.59%)p 2.76( 73.41%)
                                           -0.0017  0.5157 -0.8435 -0.1501 -0.0007
    18. (0.00034) RY*( 3) H   2           s(  0.00%)p 1.00(100.00%)
                                            0.0000  0.0004 -0.0005 -0.0001  1.0000
    19. (0.00000) RY*( 4) H   2           s(  0.72%)p99.99( 99.28%)
    20. (0.00112) RY*( 1) H   3           s( 72.77%)p 0.37( 27.23%)
                                            0.0038  0.8531  0.5218  0.0009  0.0014
    21. (0.00045) RY*( 2) H   3           s( 26.59%)p 2.76( 73.41%)
                                           -0.0017  0.5157 -0.8435  0.0756  0.1297
    22. (0.00034) RY*( 3) H   3           s(  0.00%)p 1.00(100.00%)
                                            0.0000  0.0004 -0.0005 -0.8660  0.5000
    23. (0.00000) RY*( 4) H   3           s(  0.72%)p99.99( 99.28%)
    24. (0.00112) RY*( 1) H   4           s( 72.76%)p 0.37( 27.24%)
                                            0.0038  0.8530  0.5219  0.0009 -0.0015
    25. (0.00045) RY*( 2) H   4           s( 26.61%)p 2.76( 73.39%)
                                           -0.0017  0.5158 -0.8435  0.0750 -0.1300
    26. (0.00034) RY*( 3) H   4           s(  0.00%)p 1.00(100.00%)
                                            0.0000  0.0000  0.0000  0.8660  0.5000
    27. (0.00000) RY*( 4) H   4           s(  0.72%)p99.99( 99.28%)
    28. (0.00000) BD*( 1) N   1 - H   2 
                ( 31.17%)   0.5583* N   1 s( 24.87%)p 3.02( 75.05%)d 0.00(  0.09%)
                ( 68.83%)  -0.8297* H   2 s( 99.91%)p 0.00(  0.09%)
    29. (0.00000) BD*( 1) N   1 - H   3 
                ( 31.17%)   0.5583* N   1 s( 24.86%)p 3.02( 75.05%)d 0.00(  0.09%)
                ( 68.83%)  -0.8297* H   3 s( 99.91%)p 0.00(  0.09%)
    30. (0.00000) BD*( 1) N   1 - H   4 
                ( 31.17%)   0.5583* N   1 s( 24.87%)p 3.02( 75.05%)d 0.00(  0.09%)
                ( 68.83%)  -0.8297* H   4 s( 99.91%)p 0.00(  0.09%)

 Natural Bond Orbitals (Summary):

                                                            Principal Delocalizations
           NBO                        Occupancy    Energy   (geminal,vicinal,remote)
 ====================================================================================
 Molecular unit  1  (H3N)
     1. BD (   1) N   1 - H   2          1.99909    -0.60417  
     2. BD (   1) N   1 - H   3          1.99909    -0.60417  
     3. BD (   1) N   1 - H   4          1.99909    -0.60416  
     4. CR (   1) N   1                  1.99982   -14.16768  
     5. LP (   1) N   1                  1.99721    -0.31756  24(v),16(v),20(v),17(v)
                                                    21(v),25(v)

Association Energies

Optimisation

A molecule of BH₃NH₃ was created and optimised using the B3LYP method with a 3-21G basis set: (.log file is at DOI:10042/23512 )

NH₃BH₃ optimisation 3-21G
File Name	AHall_NB_3_21
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Charge	0
Spin	Singlet
E(RB3LYP)	-82.76661837 a.u.
RMS Gradient Norm	0.00003006 a.u.
Imaginary Freq
Dipole Moment	5.8431 Debye
Point Group	C1
Job cpu time:	0 days 0 hours 1 minutes 9.7 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000094     0.000450     YES
 RMS     Force            0.000030     0.000300     YES
 Maximum Displacement     0.000419     0.001800     YES
 RMS     Displacement     0.000178     0.001200     YES
 Predicted change in Energy=-5.742850D-08
 Optimization completed.

The molecule was they further optimised using the 6-31G(d,p) basis set: (.log file is at DOI:10042/23514 )

NH₃BH₃ optimisation 6-31G(d,p)
File Name	AHall_NB_6_31
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-82.22468922 a.u.
RMS Gradient Norm	0.00005766 a.u.
Imaginary Freq
Dipole Moment	5.5623 Debye
Point Group	C1
Job cpu time:	0 days 0 hours 1 minutes 8.1 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000134     0.000450     YES
 RMS     Force            0.000037     0.000300     YES
 Maximum Displacement     0.001246     0.001800     YES
 RMS     Displacement     0.000556     0.001200     YES
 Predicted change in Energy=-1.230457D-07
 Optimization completed.

Frequency Analysis

Frequency analysis was performed on the optimised NH₃BH₃ molecule. The output .log file can be found at DOI:10042/23520 .

NH₃BH₃ optimisation 6-31G(d,p)
File Name	AHall_NB_freq
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-82.22468920 a.u.
RMS Gradient Norm	0.00005767 a.u.
Imaginary Freq
Dipole Moment	5.5623 Debye
Point Group	C1
Job cpu time:	0 days 0 hours 1 minutes 5.0 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000260     0.000450     YES
 RMS     Force            0.000058     0.000300     YES
 Maximum Displacement     0.001437     0.001800     YES
 RMS     Displacement     0.000712     0.001200     YES
 Predicted change in Energy=-2.209903D-07
 Optimization completed.
    -- Stationary point found.

Vibrations for NH₃BH₃.
Frequency	Intensity	Frequency	Intensity
262.67	0.0000	1329.09	113.7119
631.28	14.1300	1676.07	27.5527
637.66	3.5747	1676.13	27.5350
638.79	3.5764	2472.42	67.0654
1068.50	40.4761	2532.75	231.1535
1068.96	40.5518	2532.90	231.1579
1196.15	109.0108	3464.04	2.5184
1203.28	3.5024	3580.87	27.8921
1203.57	3.4862	3580.97	27.9013

 Low frequencies ---  -14.4083    0.0011    0.0012    0.0014   12.1717   17.1399
 Low frequencies ---  262.6686  631.2804  637.6627

Comparison

Energies:

NH₃ = -56.55776856 au.
BH₃ = -26.61532363 au.
NH₃BH₃ = -83.22468920 au.

Energy difference between Products and Reagents = (-83.22468920) - (-56.5577685) - (-26.61532363) = -0.05159707 au. Convert to kJmol^-1: -0.05159707 x 2625.50 = -135.455 kJmol^-1 (3d.p.)

Dissociation energy = 135.455 kJmol^-1 (lit.^[2] 31.7 kcal/mol (=132.63 kJ/mol))

Aromaticity

Benzene

Optimisation

A molecule of benzene was optimised using the B3LYP basis set and the 3-21G basis set followed by the 6-31G(d,p) basis set. The output .log files can be found at DOI:10042/23541 and DOI:10042/23543

Benzene Optimisation 6-31G(d,p)
File Name	AHall_ben_opt_6_31
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-232.25819628 a.u.
RMS Gradient Norm	0.00004042 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	C1
Job cpu time:	0 days 0 hours 2 minutes 9.2 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000090     0.000450     YES
 RMS     Force            0.000024     0.000300     YES
 Maximum Displacement     0.000337     0.001800     YES
 RMS     Displacement     0.000103     0.001200     YES
 Predicted change in Energy=-4.743663D-08
 Optimization completed.
    -- Stationary point found.

As the point group is incorrectly assigned to be C₁, the final optimization was repeated with the point group constrained to D_6h. The output .log files can be found at DOI:10042/23671 .

Benzene Optimisation 6-31G(d,p)
File Name	AHall_ben_D6h
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-232.25821426 a.u.
RMS Gradient Norm	0.00004040 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	D6H
Job cpu time:	0 days 0 hours 0 minutes 18.1 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000084     0.000450     YES
 RMS     Force            0.000029     0.000300     YES
 Maximum Displacement     0.000182     0.001800     YES
 RMS     Displacement     0.000075     0.001200     YES
 Predicted change in Energy=-4.892354D-08
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

Frequency analysis was performed on the optimised benzene molecule. The .log file can be found at DOI:10042/23673 . The low frequencies are sufficiently low that the optimisation is complete:

Low frequencies ---   -0.0088   -0.0041   -0.0041   11.3041   11.3041   15.5388
 Low frequencies ---  414.2825  414.2825  621.2723

MOs

The energy of the benzene was optimised and MOs calculated. The formatted checkpoint file can be found at DOI:10042/23675 .

The calculated MOs were analysed and a MO diagram produced for the six MOs on either side of the HOMO/LUMO gap:

NBO analysis

NBO analysis was carried out as part of the energy calculations. The carbon atoms have a charge of -0.23859 and the hydrogen atoms +0.23859 and the molecule is completely symmetrical.

The analysis also shows that the C-C bonds are formed from equal contributions of the orbitals of each carbon. The C-C bond is formed of 35% 's' atomic orbitals and 65% 'p' atomic orbitals, implying that the bonding is sp² as expected. There is also a very small contribution from 'd' orbitals (0.04%). The π bonding is shown to be formed almost entirely of 'p' orbitals, with a very small 'd' orbital contribution (0.04%). As expected the π bonding also has equal contributions from each carbon atom.

The C-H bonds contain unequal contributions from the carbon (62%) and the hydrogen (38%). The carbon contribution to the bonding is 30% 's' and 70% 'p' with a very small amount of 'd' contribution (0.04%), implying a hybridisation close to sp². The hydrogen contribution to the bonding is almost entirely due to 's' orbitals, with a very small amount of 'p' contribution (0.05%).

The core orbitals on carbon are shown to be entirely 's' orbitals.

The Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis table shows that E(2) is 20.43 kcal/mol for the interactions between the 'p' based C-C bonds, implying that there is a large amount of mixing between these orbitals and so supporting the idea of a delocalised 'p' electron cloud in aromatic molecules.

The energy of the bonding orbitals is around -0.2 to -0.6 au. whereas the core orbitals have energies of around -10 au. and so will not affect the interactions with the valence electrons.

Boratabenzene

Optimisation

Optimisation was performed on a molecule of Boratabenzene (BC₅H₆) using the B3lYP method with a 3-21G basis set followed by a 6-31G(d,p) basis set. As the point group was incorrectly determined to be C1 the second optimisation was repeated with the point group constrained to C_2v. The optimised .log file can be found at DOI:10042/23710 .

Boratobenzne optimisation
File Name	AHall_bor_opt_c2v
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	-1
Spin	Singlet
E(RB3LYP)	-219.02053052 a.u.
RMS Gradient Norm	0.00003502 a.u.
Imaginary Freq
Dipole Moment	2.8454 Debye
Point Group	C2V
Job cpu time:	0 days 0 hours 0 minutes 23.4 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000062     0.000450     YES
 RMS     Force            0.000018     0.000300     YES
 Maximum Displacement     0.000218     0.001800     YES
 RMS     Displacement     0.000071     0.001200     YES
 Predicted change in Energy=-3.182072D-08
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

As the low frequencies are low compared to the 'real' frequencies, and none of the 'real' frequencies are negative the optimisation was successful. A link to the .log file can be found at DOI:10042/23724 .

 Low frequencies ---  -12.4155   -0.0008   -0.0003    0.0006   14.0145   18.0525
 Low frequencies ---  371.3796  404.1483  565.1933

MOs

The MOs for boratabenzene are shown below. A link to the relevant files can be found at DOI:10042/23723 .

The presence of the boron atom strongly disrupts the shape of the MOs; for some MOs the boron atom contributes more to the MO than the carbon atoms (eg. MOs 16, 18, 19, 21), and for some MOs the boron is contributing less to the MO (eg. 17, 24, 28). This can be explained by considering the difference in electronegativity between carbon and boron. As the boron is more electropositive than carbon (and hydrogen) the atomic orbitals of boron will be higher in energy than those for carbon. This means that the boron contributes less to bonding interactions than to anti-bonding interactions; for example in MO 17, all of the interactions are bonding, so the boron contributes less, and for MO 23 the interactions are anti-bonding so the boron contributes more.

MOs for Boratabenzene
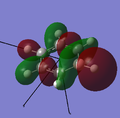
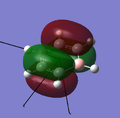
MO 16	MO 17	MO 18	MO 19	MO 20
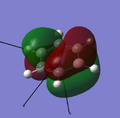
MO 21	MO 22	MO 23	MO 24	MO 25
MO 26	MO 27	MO 28

NBO anaylsis

The analysis also shows that the C-C bonds are formed from nearly equal contributions of the orbitals of each carbon. The C-C bond is formed of 36% 's' atomic orbitals and 64% 'p' atomic orbitals, implying that the bonding is close to sp². There is also a very small contribution from 'd' orbitals (0.04%). The π bonding is shown to be formed almost entirely of 'p' orbitals, with a very small 'd' orbital contribution (0.03%). As expected the π bonding also has equal contributions from each carbon atom.

The C-H bonds vary considerable around the ring (unlike in benzene where they are all equal) with some cases the carbon being close to sp² (70% 'p', 30% 's') and in others (closer to the boron) the carbon is nearly sp³ (74% 'p', 25% 's'). The carbon generally contributes to about 60% with the remainder being made up by the hydrogen 's' orbital.

The C-B bond is formed from about 66% carbon (42% 's', 58% 'p') and 33% boron (33% 's', 67% 'p'). The B-H bond is 55% hydrogen and 45% boron, with the boron atom as sp² (33% 's', 67% 'p') and the hydrogen entirely 's'.

The core orbitals on carbon and boron are shown to be entirely 's' orbitals.

Lone pairs have been assigned to the boron and the carbon directly opposite the boron, both with entirely 'p' character.

Significant mixing is observed for the π bonds on carbon, with a small amount of mixing between the lone pair on boron and the π bonds for carbon indicating that the molecule has some aromatic behaviour.

Pyridinium

Optimisation

A pyridinium ion was optimised using the B3LYP method with the 3-21G basis set followed by the 6-31G(d,p) basis set. The optimised .log file can be found at DOI:10042/23745 .

Pyridinium Optimisation
File Name	AHall_pyr_opt_6_31
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	1
Spin	Singlet
E(RB3LYP)	-248.66807392 a.u.
RMS Gradient Norm	0.00004765 a.u.
Imaginary Freq
Dipole Moment	1.8719 Debye
Point Group	C2V
Job cpu time:	0 days 0 hours 1 minutes 13.7 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000086     0.000450     YES
 RMS     Force            0.000028     0.000300     YES
 Maximum Displacement     0.000672     0.001800     YES
 RMS     Displacement     0.000207     0.001200     YES
 Predicted change in Energy=-1.043954D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

As the low frequencies are low compared to the 'real' frequencies, and non of the 'real' frequencies are negative, the optimisation has completed. The .log file can be found at DOI:10042/23970 and DOI:10042/23962 .

 Low frequencies ---   -6.9726   -0.0004   -0.0003    0.0006   17.3253   18.4293
 Low frequencies ---  392.5033  404.0211  620.5147

MOs

Energy calculation was performed on the optimised pyridinium ion. The output files can be found at DOI:10042/23983

The opposite trend to that for boron is observed, as the nitrogen is more electrophilic than carbon and so has lower energy atomic orbitals. As the nitrogen orbitals are lower in energy they contribute more to the bonding orbitals than to the anti-bonding orbitals. This can be seen in the MOs below, as the bonding interactions in MOs 17 and 24 have much larger contributions from nitrogen than the anti-bonding interactions in MOs 18, 20, 22 and 25.

MOs for Boratabenzene
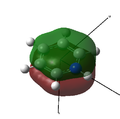
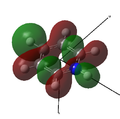
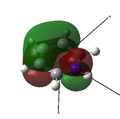
MO 16	MO 17	MO 18	MO 19	MO 20
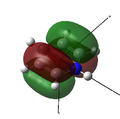
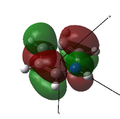
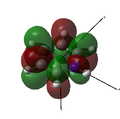
MO 21 (LUMO)	MO 22 (HOMO)	MO 23	MO 24	MO 25
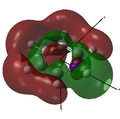
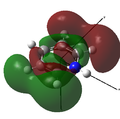
MO 26	MO 27

NBO analysis

The NBO analysis of pyridinium indicates more similarities with benzene than boratabenezene, as the C-C bonds contain roughly equal contributions from both atoms and are sp² with 33% 's' and 67% 'p'. The C-C π bonds are entirely 'p' based and contain equal contributions from each carbon atom. The C-H bonds are 65% carbon and 35% hydrogen with the carbon 31% 's' and 69% 's'.

The C-N bond is 37% C and 63% N, with carbon using 28% 's' and 72% 'p' and nitrogen using 37% 's' and 63% 'p'. C-N π bonds are also observed with 28% carbon contribution and 71% nitrogen with entirely 'p' orbitals. The N-H bond is 25% hydrogen and 75% nitrogen (27% 's', 73% 'p').

The core orbitals of carbon and nitrogen are entirely 's' based.

Significant mixing between the C-C and C-N π bonds is observed, implying that the system is aromatic.

Borazine

Optimisation

A molecule of borazine was optimised using the B3LYP method with the 3-21G basis set followed by the 6-31G(d,p) basis set. The .log files can be found at DOI:10042/23974 and DOI:10042/23975 .

Borazine Optimisation
File Name	AHall_borz_opt_6_31
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-242.68458200 a.u.
RMS Gradient Norm	0.00010596 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	D3H
Job cpu time:	0 days 0 hours 0 minutes 50.0 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000110     0.000450     YES
 RMS     Force            0.000047     0.000300     YES
 Maximum Displacement     0.000527     0.001800     YES
 RMS     Displacement     0.000204     0.001200     YES
 Predicted change in Energy=-3.565285D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

All of the low frequencies are much lower than the 'real' frequencies, and none of the 'real' frequencies are negative, indicating that the optimisation was successful. The .log file for the frequency analysis can be found at DOI:10042/23978 .

 Low frequencies ---  -14.3764  -14.0440  -10.4678   -0.0163   -0.0114    0.0336
 Low frequencies ---  289.0878  289.0895  404.1828

MOs

Energy calculations were performed on the optimised borazine. The output files can be found at DOI:10042/23982 .

MOs for Borazine
MO 16	MO 17	MO 18	MO 19	MO 20
MO 21 (LUMO)	MO 22 (HOMO)	MO 23	MO 24	MO 25
MO 26	MO 27

NBO analysis

The framework in borazine is made up from B-N bonds which are made up of 76% nitrogen (s( 38.56%), p( 61.43%)) and 24% boron (s( 31.24%), p( 68.51%)). The π bonds are 88% N and 22% B and are entirely 'p' based.

The B-H bonds are 45% boron (s( 37.48%),p( 62.45%)) and 55% hydrogen. The N-H bonds are 71% nitrogen (s(22.81%), p( 77.16%)) and 29% hydrogen.

The core orbitals on boron and nitrogen are entirely 's' based.

Mixing is observed between the B-N π framework, indicating that the molecule is aromatic.

Comparison

Charge Distribution

Benzene		Boratabenzene		Pyridinium		Borazine


Carbon 1	-0.239	Carbon 1	-0.250	Carbon 1	-0.241	Boron 1	0.747
Carbon 2	-0.239	Carbon 2	-0.588	Carbon 2	0.071	Nitrogen 2	-1.102
Carbon 3	-0.239	Boron 3	0.202	Nitrogen 3	-0.476	Boron 3	0.747
Carbon 4	-0.239	Carbon 4	-0.588	Carbon 4	0.071	Nitrogen 4	-1.102
Carbon 5	-0.239	Carbon 5	-0.250	Carbon 5	-0.241	Boron 5	0.747
Carbon 6	-0.239	Carbon 6	-0.340	Carbon 6	-0.122	Nitrogen 6	-1.102
Hydrogen 7	0.239	Hydrogen 7	0.186	Hydrogen 7	0.292	Hydrogen 1	0.432
Hydrogen 8	0.239	Hydrogen 8	0.179	Hydrogen 8	0.297	Hydrogen 1	-0.077
Hydrogen 9	0.239	Hydrogen 9	0.184	Hydrogen 9	0.285	Hydrogen 1	0.432
Hydrogen 10	0.239	Hydrogen 10	-0.097	Hydrogen 10	0.483	Hydrogen 1	-0.077
Hydrogen 11	0.239	Hydrogen 11	0.184	Hydrogen 11	0.285	Hydrogen 1	0.432
Hydrogen 12	0.239	Hydrogen 12	0.179	Hydrogen 12	0.297	Hydrogen 1	-0.077
Total	0	Total	-1	Total	+1	Total	0

As expected the charge on benzene is very low, and all carbon atoms are identical, as are all hydrogen atoms. The charge on borazine - also relatively symmetrical - is much higher. Due to the symmetry there is no overall dipole, however due to the differences in electronegativity the boron atoms are very strongly positively charged, and the nitrogen atoms negatively charged. The charge on boron/nitrogen induces a smaller opposing charge on the hydrogen atoms which are attached to them.

Both boratabenzene and pyridinium have unsymmetrical charge on the carbon atoms, with those located closest to the heteroatom having greater charge. The boron atom has a positive charge which induces a more negative charge onto the neighboring carbon and hydrogen atoms. For the carbon atoms which are already partially negatively charged this reinforces the charge, making the carbon atoms more negative; however for hydrogen which is normally positively charged this opposes the charge, making the hydrogen atom less strongly charged. As the nitrogen atom in pyridinium has a negative charge this causes the opposite effect to boron, with the neighboring carbon atoms having an small induced positive charge and the neighboring hydrogen atom having its positive charge reinforced.

The charges in pyridinium are greater than in boratabenzene as the difference in electronegativities between carbon and nitrogen are greater than the difference between carbon and boron. The largest charge difference is for borazine, as this molecule contains alternative electropositive and electronegative atoms. The smallest charge difference is for benzene as there is no difference in electronegativities between the ring atoms, and the difference in electronegativities between carbon and hydrogen are small.

MOs

MO 17

Benzene	Boratabenzene	Pyridinium	Borazine

The MOs for benzene and borazine are symmetrical, whereas those for boratabenzene and pyridinium are asymmetric due to the presence of the heteroatom. The nitrogen orbital contributes more to the MO as nitrogen is more electronegative than carbon, and so has atomic orbitals which are lower in energy, and so contribute more to the bonding orbitals than to the anti-bonding orbitals. The opposite is true for boron as boron is less electronegative than carbon and so has orbitals higher in energy which contribute less to bonding orbitals and more to anti-bonding orbitals.

MO 18/19

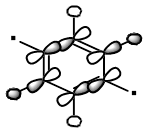
	Benzene	Boratabenzene	Pyridinium	Borazine
MO 18
MO 19

As this MO contains significant anti-bonding character the opposite effect to MO 17 can be observed, with boron contributing more to the MO than nitrogen due to its lower electronegativity. MOs 18 and 19 are degenerate for benzene and borazine, however for boratabenzene and pyridinium there is a significant difference in energy (0.00789 au. for borazine and 0.00296 au. for pyridine). This difference in energy is due to the asymmetry that the heteroatom induces. For pyridinium the higher energy MO has the same shape as the MO 19 for benzene, whereas for boratabenzene the MO with this shape is of lower energy.

MO 20/21

	Benzene	Boratabenzene	Pyridinium	Borazine
MO 20
MO 21

As with MOs 18 and 19, MOs 20 and 21 are degenerate for benzene and borazine, but not for boratabenzene and pyridinium. As the MOs with the same shape as MO 20 on benzene do not include the heteroatom for boratabenzene and pyridinium, these MOs are largely undistorted, however for borazine the contribution from nitrogen is significantly bigger than the contribution from boron as the orbital is bonding and so electronegative atoms contribute more than electropositive atoms. As was the case for MOs 18 and 19 the ordering is different for boratabenzene and pyridinium, probably due to the increased antibonding effects in MO 21 of boratabenzene compared to MO 20 of pyridinium due to the less electronegative boron atom contributing more.

The MOs with the same shape as MO 21 in benzene are much more varied, with the boron lobe in the boratabenzene being much larger than the nitrogen lobe in pyridinium due to the antibonding interactions in the orbital favouring the less electronegative atom. MO 21 for borazine is particularly interesting as the orbital is unsymmetrical due to the lack of a xz plane of symmetry meaning that there are two nitrogen atoms and one boron forming half of the MO, and the other half is formed of two borons and one nitrogen atom.

Effects on full MO diagram

Substituting a single boron or nitrogen atom into the ring causes a loss of symmetry, and therefore a loss of degeneracy between orbitals. This means that the MO diagrams for boratabenzene and pyridinium would not have as much degeneracy as for benzene, however as the difference in energy of the orbitals due to the loss of symmetry is low, the previously degenerate orbitals would still be close together. For borazine there is less loss of symmetry and so there would be more degenerate orbitals on the MO diagram.

References

↑ ^1.0 ^1.1 ^1.2 ^1.3 D. R. Lide, CRC handbook of chemistry and physics., CRC ;, Boca Raton, Fla., 93rd ed., 2012.
↑ Li,Jun; Kathmann,Shawn M.; Hu, Han-Shi; Schenter, Gregory K.; Autrey, Tom; and Gutowski, Maciej; Inorg. Chem., 2010, 49 (17), pp 7710–7720 DOI:10.1021/ic100418a

[CRC-1] 1.0 ^1.1 ^1.2 ^1.3 D. R. Lide, CRC handbook of chemistry and physics., CRC ;, Boca Raton, Fla., 93rd ed., 2012.

[Li-2] Li,Jun; Kathmann,Shawn M.; Hu, Han-Shi; Schenter, Gregory K.; Autrey, Tom; and Gutowski, Maciej; Inorg. Chem., 2010, 49 (17), pp 7710–7720 DOI:10.1021/ic100418a

[1]

[2]

Bonding and Molecular Orbitals in Main Group Compounds

Optimisation of BH3

Using 3-21G basis set

Using 6-31G(d,p) basis set

Pseudo-Potentials

Optimisation of TlBr3

Optimisation of BBr3

Comparison of Bond lengths

Frequency Calculations

BH3

Optimisation

Frequency Analysis

TlBr3

Comparison

MOs

BH3

NBO Analysis

NH3

Optimisation

Frequency Analysis

Molecular Orbitals

NBO analysis

Association Energies

Optimisation

Frequency Analysis

Comparison

Aromaticity

Benzene

Optimisation

Frequency Analysis

MOs

NBO analysis

Boratabenzene

Optimisation

Frequency Analysis

MOs

NBO anaylsis

Pyridinium

Optimisation

Frequency Analysis

MOs

NBO analysis

Borazine

Optimisation

Frequency Analysis

MOs

NBO analysis

Comparison

Charge Distribution

MOs

MO 17

MO 18/19

MO 20/21

Effects on full MO diagram

References

Optimisation of BH₃

Optimisation of TlBr₃

Optimisation of BBr₃

BH₃

TlBr₃

BH₃

NH₃