Rep:Mod:AGB201113
Synthesis and Computational Lab: 1C
Introduction: Part 1
The foundations of force field methods are atoms, rather than electrons and therefore, the bonding information cannot be solved from the electronic Schrodinger equation. In addition, the nuclei are treated classically rather than quantum mechanically (ball and spring model)[1]. Force field methods also assume that atoms and bonds are not fixed at one size and bond length, i.e. they are vibrating. In this report, force field methods are used to find geometries of stable molecules and their different conformations and consequently finding energy minima. A possible drawback of using the force field method is that it does not account for any error within the method, i.e. it is "zero-dimensional". This means that the data obtained must usually be backed up by experimental data[2].
The Hydrogenation of the Cyclopentadiene Dimer
Molecules 1 and 2 shown below are the two possible products resulting from the dimerisation of cyclopentadiene. A molecular mechanics technique was used to obtain information about whether the cyclodimerisation of cyclopentadiene and the following hydrogenation of the dimer were thermodynamically or kinetically controlled. This was done by computing the geometries and energies of the dimers using an MM2 force field in ChemBio3D. Cyclopentadiene dimerises specifically to the endo dimer (2) rather than the exo dimer (1). The dimerisation of cyclopentadiene is a bispericyclic reaction which proceeds via a [3,3] sigmatropic shift and a simultaneous π2s + π4s/π4s + π2s cycloaddition[3]. The transition state proceeds via a Huckel intermediate (4n+2e + heat; proceeds suprafacially with disrotation). The dimer with the lowest transition state energy gives the endo product. However, it was found that the endo dimer (2) had a higher total energy (33.9975 kcal/mol) than the exo dimer (1) (31.8765 kcal/mol). This indicates that the exo isomer is in fact the thermodynamic product rather than the observed endo isomer. Therefore, we can conclude that the dimerisation is kinetically controlled with the endo isomer having the greater transition state stability. The main component that makes the energies of the two isomers different is the torsional strain (1.8566 kcal/mol higher in the endo isomer). The torsional strain is higher in the endo isomer since there is more Pauli bond repulsion due to the carbon frameworks being closer to each other.
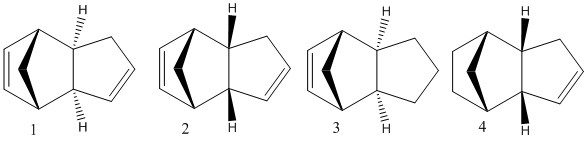
| Property | Dimer 1 | Dimer 2 | Dimer 3 | Dimer 4 |
|---|---|---|---|---|
| Stretch | 1.2850 | 1.2500 | 1.235 | 1.0965 |
| Bend | 20.5804 | 20.8493 | 18.9392 | 14.5227 |
| Stretch-bend | -0.8383 | -0.8357 | -0.7608 | -0.5495 |
| Torsion | 7.6543 | 9.5109 | 12.1232 | 12.4978 |
| 1,4 VDW | 4.2336 | 4.3189 | 5.7291 | 4.5127 |
| Dipole/Dipole | 0.3775 | 0.1631 | 0.1637 | 0.1406 |
| Total energy | 31.8765 kcal/mol | 33.9975 kcal/mol | 35.9266 kcal/mol | 31.1521 kcal/mol |
The hydrogenation of the endo dimer (2) results in the two dimers 3 and 4. It can be concluded from the total energy of dimer 4 (31.1521 kcal/mol) that it is the more stable dimer compared to the energy of dimer 3 (35.9266 kcal/mol). The stability of the double bond is what determines the stability of dimers 3 and 4. We can conclude therefore that the double bond is most stable in a 5-membered ring than in a bridged 6-memebered ring. This stability can be rationalised if we look at the Bend energy. It is 4.4165 kcal/mol higher in 3 than in 4. Even though optimised cyclohexene is more stable than optimised cyclopentene, the bridging structure reduces the internal angles of the 6-membered ring which puts strain on the ring and consequently raises the energy. Since this is the largest differing energy component, we can conclude that this is the contributing factor to the stability of dimer 4.
Atropisomerism in an Intermediate Related to the Synthesis of Taxol
Configurational and conformational isomers (atropisomers) 9 and 10 were investigated to find the most stable isomer. The results show the 4 different energy minima resulting from the differing conformations the cyclohexane ring can exist in:
| Property | Chair 1 | Twist Boat 1 | Twist Boat 2 | Chair 2 |
|---|---|---|---|---|
| Stretch | 2.7839 | 2.9482 | 2.8790 | 3.3212 |
| Bend | 16.5443 | 17.2096 | 17.2786 | 20.4952 |
| Stretch-bend | 0.4299 | 0.5010 | 0.4731 | 0.4986 |
| Torsion | 18.2569 | 21.2856 | 20.6072 | 22.0149 |
| 1,4 VDW | 13.1100 | 14.5039 | 14.3725 | 14.9632 |
| Dipole/Dipole | -1.7252 | -1.7305 | -1.7088 | -1.8326 |
| Total energy | 47.8397 kcal/mol | 53.3044 kcal/mol | 53.0099 kcal/mol | 58.3858 kcal/mol |
| Property | Chair 1 | Twist Boat 1 | Twist Boat 2 | Chair 2 |
|---|---|---|---|---|
| Stretch | 2.6218 | 2.8341 | 2.7106 | 3.3212 |
| Bend | 11.3409 | 12.9807 | 11.7412 | 20.4952 |
| Stretch-bend | 0.3436 | 0.3903 | 0.3236 | 0.4986 |
| Torsion | 19.6675 | 22.9739 | 21.8696 | 22.0149 |
| 1,4 VDW | 12.8707 | 14.1187 | 13.9197 | 14.9632 |
| Dipole/Dipole | -2.0024 | -2.0322 | -2.0315 | -1.8326 |
| Total energy | 42.6829 kcal/mol | 49.5133 kcal/mol | 46.4336 kcal/mol | 58.3858 kcal/mol |
In both cases (atropisomer 9 and 10) the total energy of the a chair conformation is higher than the twist boat conformations, whereas normally, the twist boat minima are higher in energy than the chair minima.
Overall, the most stable atropisomer is 10, since its most stable minima (Chair 1) has the lowest total energy (42.6829 kcal/mol) compared to the most stable minima in 9 (Chair 1 at 47.8397 kcal/mol).
This can be rationalised by the idea that the reactivity of alkenes is controlled by the stability of the intermediate carbocation (with tertiary carbocations being most stable through a high level of sigma conjugation). In reality, this alkene reacts much slower than expected since it is a hyperstable alkene due to the bridged-ring structure[4]. The bridged-ring structure does not allow for the formation of a planar carbocation intermediate, thereby increasing the energy of the carbocation transition state, and affecting the rate of reactivity of the alkene. From Hammond's postulate we can deduce that since the transition state energy is high, the energy of the carbocation intermediate will also be high.
Spectroscopic Simulation using Quantum Mechanics
For the molecule below (17), the 1H and 13C spectra were simulated and compared to the literature values[5] to see whether they were accurate or not. The NMR spectra generated in the literature were carried out in CDCl3 solvent on a 300 MHz spectrometer for 1H and a 75 MHz spectrometer for 13C.
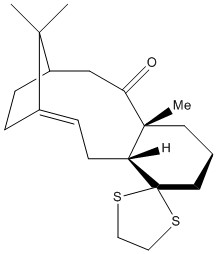
The results from the initial optimisation of molecule 17 are shown below:
| Property | 17 |
|---|---|
| Stretch | 4.9996 |
| Bend | 22.8522 |
| Stretch-bend | 0.7665 |
| Torsion | 20.9565 |
| 1, 4 VDW | 15.7982 |
| Dipole/Dipole | -2.1621 |
| Total Energy | 63.9637 kcal/mol |
1H NMR Spectrum of 17:
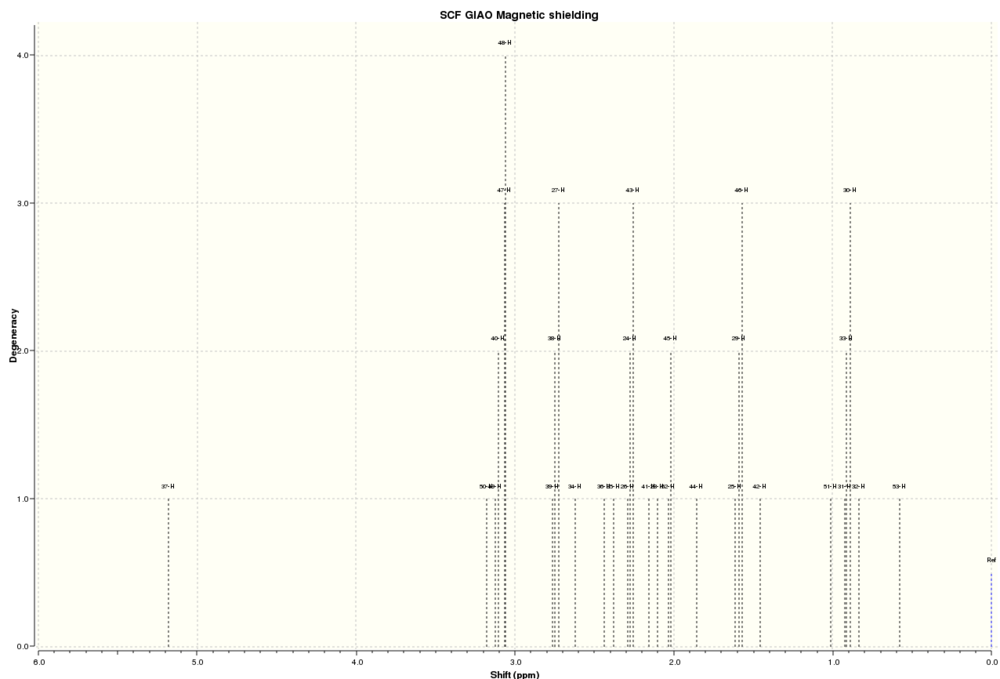
By comparing the literature values of the chemical shifts for molecule 17, we can deduce how far the computed structure is from its natural state.
| Atoms | Computed Chemical Shifts (ppm) | Literature Chemical Shifts (ppm) |
|---|---|---|
| 37 | 5.18 | 4.84 |
| 50 | 3.18 | 3.10 - 3.40 |
| 49,40,47,48 | 3.09 | 3.10 - 3.40 |
| 39,38,27 | 2.74 | 2.99 |
| 34 | 2.62 | 1.35 - 2.80 |
| 36 | 2.44 | 1.35 - 2.80 |
| 35 | 2.38 | 1.35 - 2.80 |
| 26,24,43 | 2.27 | 1.35 - 2.80 |
| 41 | 2.16 | 1.35 - 2.80 |
| 28 | 2.10 | 1.35 - 2.80 |
| 52,45 | 2.03 | 1.35 - 2.80 |
| 44 | 1.85 | 1.35 - 2.80 |
| 25,29,46 | 1.59 | 1.35 - 2.80 |
| 42 | 1.46 | 1.38 |
| 51 | 1.01 | 1.10 |
| 31,33,30 | 0.91 | 0.80 - 1.00 |
| 32 | 0.84 | 0.80 - 1.00 |
| 53 | 0.58 |
Analysis and Comparison of NMR Chemical Shifts:
- Atom number 37 is due to the only allylic proton which is to be expected at around 5 ppm. The computed value has a lower field than the literature value indicating that it is more deshielded. This is most likely due to the large electron cloud around the sulphur atoms that spreads out towards the double bond and increases the electron density surrounding it leading to a deshielding effect. Another possibility would be the electron density from the carbonyl oxygen. Since in molecule 17, the carbonyl is pointing upwards, the allylic proton is on the same face as the carbonyl and is consequently in close proximity.
- The next highest chemical shifts are those due to hydrogens alpha to sulphur (expected at 3.00 - 3.50 ppm). A pair of hydrogens alpha to sulphur 20 (hydrogens 49 and 50) and a pair alpha to sulphur 19 (hydrogens 47 and 48). Atoms 47 and 49 should be degenerate in chemical shift due to the C2 axis through the 5-membered dithiolane ring, which is in good accordance with the Gaussian computed spectrum. Atom 50 has a slightly lower field chemical shift compared to the other hydrogens alpha to sulphur atoms. This could be due to its slightly closer proximity to the center of the 5-membered ring which contains the most electron density (since it is between two electron rich sulphur atoms).
- The ordering of the chemical shifts for the remaining protons depends strongly on which face of the molecule they are on. Those that point upwards, in the same direction of the carbonyl oxygen tend to be of a lower field shift than those that point downwards away from the oxygen. This is again due to the deshielding nature of the electronegative oxygen atom.
- Those hydrogens that are part of the decane ring, seem to have lower field chemical shifts as well, which might suggest a concentration of electron density through the decane ring. This can be deduced because some hydrogens that would otherwise have higher field chemical shifts (alkyl protons for example) are computed to have considerably lower field chemical shifts than expected.
- In general, when compared with the literature values have a lower field chemical shift. Gaussian is known to make this systematic error for all NMR calculations as it overestimates the deshielding effects on the nucleus[6].
13C NMR Spectrum of 17:
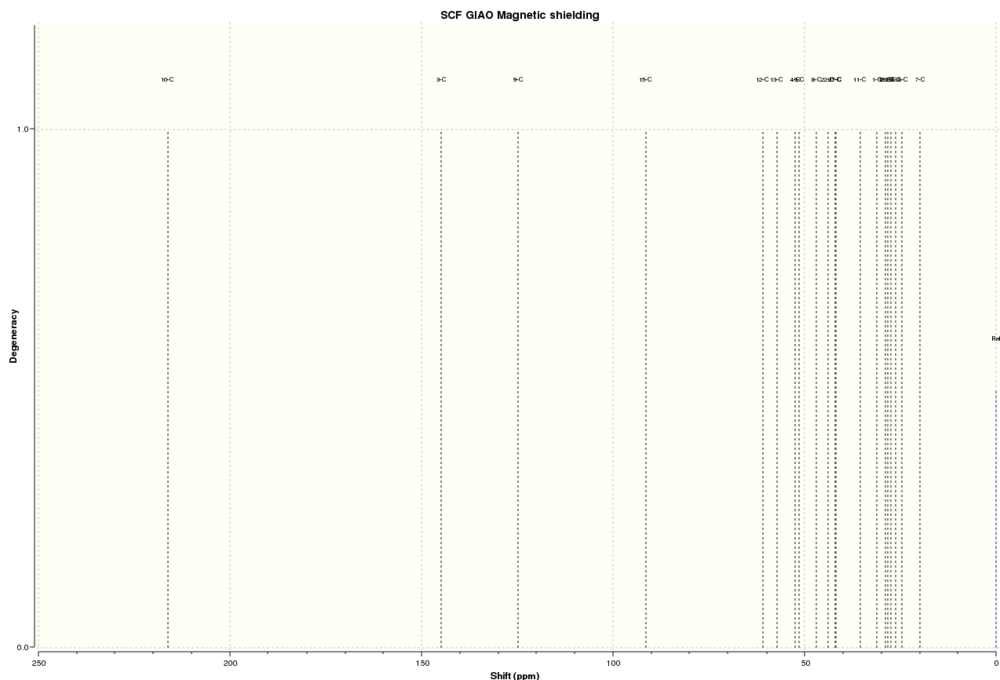
| Atoms | Computed Chemical Shifts (ppm) | Literature Chemical Shifts (ppm) |
|---|---|---|
| 10 | 216.27 | 218.79 |
| 3 | 144.86 | 144.63 |
| 9 | 124.72 | 125.33 |
| 15 | 91.37 | 72.88 |
| 12 | 60.96 | 56.19 |
| 13 | 57.08 | 52.52 |
| 4 | 52.47 | 48.50 |
| 5 | 51.49 | 46.80 |
| 8 | 46.92 | 45.76 |
| 22 | 43.88 | 39.80 |
| 21 | 41.94 | 38.81 |
| 17 | 41.87 | 38.81 |
| 11 | 35.44 | 35.85 |
| 1 | 31.20 | 32.66 |
| 16 | 28.94 | 28.79 |
| 23 | 28.36 | 28.29 |
| 2 | 27.38 | 26.88 |
| 6 | 26.33 | |
| 18 | 24.55 | 25.66 |
| 23.86 | ||
| 20.96 | ||
| 7 | 19.78 | 18.71 |
- Atom 10 has the lowest field chemical shift since it is directly bonded to the carbonyl oxygen which is electron withdrawing and therefore deshields the carbon 10. The next lowest field chemical shift is due to the allylic carbons (atoms 3 and 9) which are deshielded due to the alkene ring current. These two carbons have similar chemical shifts. Next is carbon 15 which is in between two highly electron rich sulphur atoms, making it very deshielded.
- Atoms 12 and 13 are in between carbon 15 and carbon 10. They have the next lowest chemical shifts since the effects felt by the carbonyl oxygen and the oxygen between the sulphur atom affect these carbons as well.
- Comparing the computed chemical shifts to the literature, in general there is a good match. However, an interesting point to note is that the chemical shift for carbon 15 has a much higher ppm predicted by Gaussian than the literature reports (18.49 ppm higher). This suggests that there is less electron density from the two sulphur atoms in reality than what Gaussian predicts.
Vibrational Analysis of 17
| Component | Energy (Hartree/Particle) |
|---|---|
| Zero-point correction | 0.468395 |
| Thermal correction to Energy | 0.489750 |
| Thermal correction to Enthalpy | 0.490694 |
| Thermal correction to Gibbs Free Energy | 0.422008 |
| Sum of electronic and zero-point Energies | -1651.414386 |
| Sum of electronic and thermal Energies | -1651.393031 |
| Sum of electronic and thermal Enthalpies | -1651.392087 |
| Sum of electronic and thermal Free Energies | -1651.460772 |
The Gibbs free energy here is defined by the 'Sum of electronic and thermal Free Energies' component and is given in Hartrees as -1651.460772. This is converted into kJ/mol using the relationship: 1 Hartree = 2625.50 kJ/mol to give the result below:
ΔG for molecule 17 = -4335900 kJ/mol
Introduction: Part 2
This part of the module is dedicated to examining the asymmetric epoxidations of various alkenes using the Jacobsen and Shi catalysts. In particular, the chiroptical properties of the resulting epoxides will be computed, as well as the transition state energies of the Jacobsen and Shi epoxidation. This result will then be used to determine the enantiomeric excess of the epoxidations. The NMR of the resulting epoxides was also computed, analysed and compared to literature values.
Stable Precursor to Shi Catalyst (21) [7]
Please right-click on the Jmol picture ---> "Style" ---> "Labels" ---> "With atom no.", to make sense of the bond numbering.
Pentahelicene |
| C-O Bond | Length (A) | Part of Anomeric Centre? |
|---|---|---|
| 1 -2 | 1.429 | No |
| 15 - 2 | 1.423 | Yes |
| 4 - 15 | 1.454 | Yes |
| 3 - 4 | 1.423 | Yes |
| 3 - 12 | 1.415 | Yes |
| 12 - 11 | 1.434 | No |
| 9 - 10 | 1.437 | No |
| 10 - 16 | 1.428 | Yes |
| 16 - 8 | 1.456 | Yes |
| 8 - 7 | 1.415 | No |
- The alpha anomer of a cyclohexane ring is stabilised by donation of the lone pair on oxygen into the antibonding orbital of the C-O bond. The optimised structure has the lowest energy transition state as the boat conformer, but the chair conformation is the only conformation that benefits from stabilisation from the anomeric effect (due to the syn-periplanar relationship that results giving maximum orbital overlap).
- Bond 3-12 is the shortest C-O bond that is part of an anomeric centre since it benefits from this syn-periplanar arrangement of the lone pair and antibonding orbital. This results in shortening of the bond because the anomeric effect here is maximised and the electron density between the carbon and oxygen atom is maximised resulting in an increase in bond order.
- The 5-membered ring consisting of bonds: 9-10, 10-16, 16-8 and 8-7 is in a half chair conformation. The bond length for the 10-16 bond (1.428 A) is shorter than for the 16-8 bond (1.456 A), meaning that it has better orbital overlap between the oxygen lone pair and the antibonding C-O sigma orbital. Since bonds 8-7 and 9-10 are not part of the anomeric centre, there is no anomeric stabilisation since there is no available C-O antibonding orbital to donate a lone pair of electrons in to. Because of this, it is expected that these bonds should be longer than their anomeric counterparts, however they are not, indicating that there is no relationship between the bond length and the stabilisation benefit from the anomeric effect.
- The 5-membered ring consisting of bonds: 3-4, 4-15, 15-2 and 1-2 is in an envelope conformation. Bonds 3-4, 4-15 and 15-2 are able to be stabilised by the anomeric effect, whereas 1-2 is not. Again, it is expected therefore that bond 1-2 is longer than the other three, but again there is no relationship between stabilisation and bond length since the 1-2 bond is shorter than 4-15.
- The lack of a relationship between stabilisation and bond length could be due to strain effects from the 5-membered rings or steric effects.
Pre-Catalyst to Jacobsen (23)[8]
23 |
- Interactions between two hydrogen atoms become repulsive when the distance between them becomes less than the sum of the van der Waals radius. For hydrogen this radius it 1.2 Å[9] . Therefore, the maximum attraction is when the distance is 2.4 Å and becomes repulsive at < 2.1 Å.
- There are two groups of close approaching tert-butyl groups, one group on the same face as the chlorine atom and another on the opposite face as the chlorine atom. The hydrogen atoms on the tert-butyl groups come into close contact on both sides. On the same face as the chlorine atom, the distance between the two hydrogen atoms is 0.264 nm and the distance between hydrogen atoms on the opposite face of the chlorine atom is 0.242 nm, as can be seen from the molecule above. This results in two attractive interactions. The interactions of the hydrogens on the opposite face of the chlorine atom are more attractive than on the same face as the chlorine atom because 0.242nm is closer to the maximum attraction length of 0.24 nm than 0.264 nm is.
- Another interesting feature of this pre-catalyst is that the salen ligand has lost its disymmetry upon coordinating to the manganese and the whole molecule comes closer to planarity (but not total planarity as can be seen from the curved nature of the molecule). Also, it is interesting to note that the cyclohexane ring is in the chair conformation, and therefore we can assume that this is the most stable conformation for the ring.
NMR Epoxides
1HNMR dihydronaphthalene oxide:
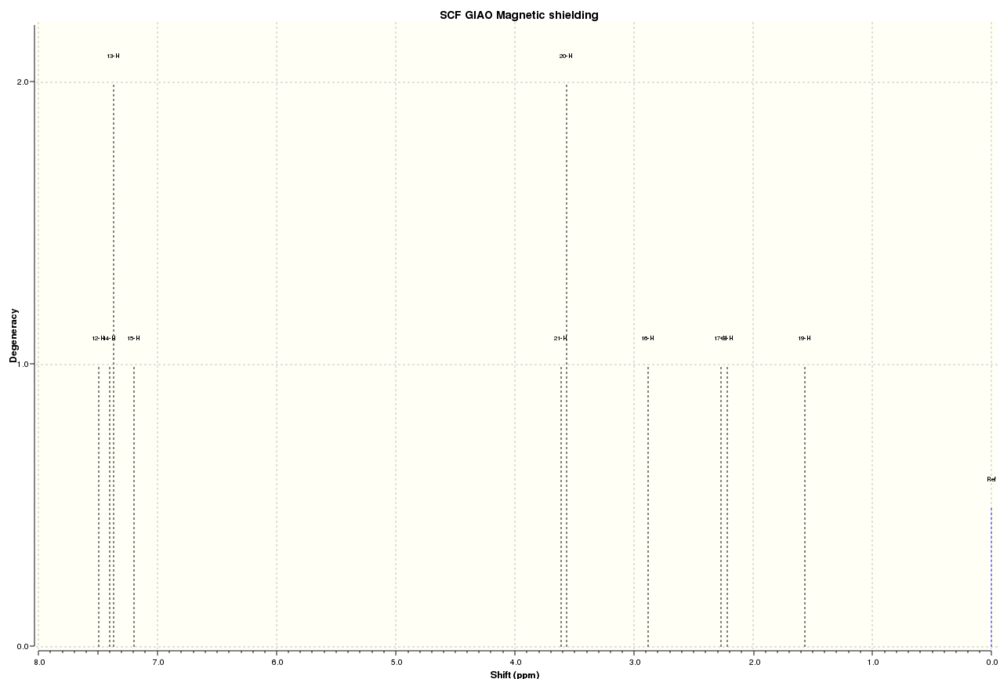
| Atoms | Computed Chemical Shifts (ppm) | Literature Chemical Shifts (ppm)[10] |
|---|---|---|
| 12 | 7.49 | 7.33 |
| 14, 13 | 7.39 | 7.14 - 7.21 |
| 15 | 7.20 | 7.01 |
| 21, 20 | 3.59 | 3.65 - 3.78 |
| 16 | 2.88 | 2.65 - 2.70 |
| 17 | 2.27 | 2.45 |
| 18 | 2.22 | 2.31 - 2.39 |
| 19 | 1.56 | 1.60 - 1.70 |
From the table above it is clear that the computed chemical shifts match up to the literature values very well, with some computed chemical shifts being slightly lower field than the literature due to the Gaussian program which always results in slightly higher ppm chemical shifts as mentioned before in Part 1.
13CNMR dihydronaphthalene oxide:
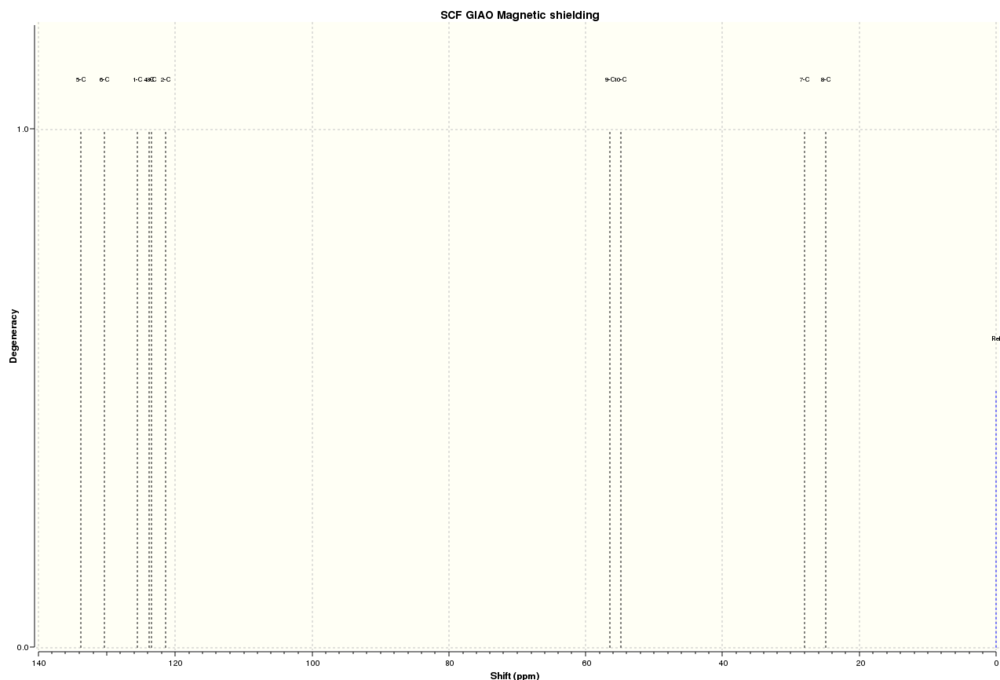
| Atoms | Computed Chemical Shifts (ppm) | Literature Chemical Shifts (ppm)[10] |
|---|---|---|
| 5 | 133.84 | 137.10 |
| 6 | 130.38 | 132.90 |
| 1 | 125.55 | 129.90 |
| 4 | 123.84 | 128.80 |
| 3 | 123.43 | 128.80 |
| 2 | 121.44 | 126.50 |
| 9 | 56.43 | 55.50 |
| 10 | 54.83 | 55.20 |
| 7 | 28.04 | 24.80 |
| 8 | 24.95 | 22.20 |
Again, the computed chemical shifts are a good match to the literature values. However, the computed chemical shifts tend to be of a higher field than the literature values, which is not expected and not what we have seen in the previous cases. Since we expect Gaussian to exaggerate the deshielding effect this is something that is unexpected and could be a source of investigation in another review.
1H NMR Stilbene:
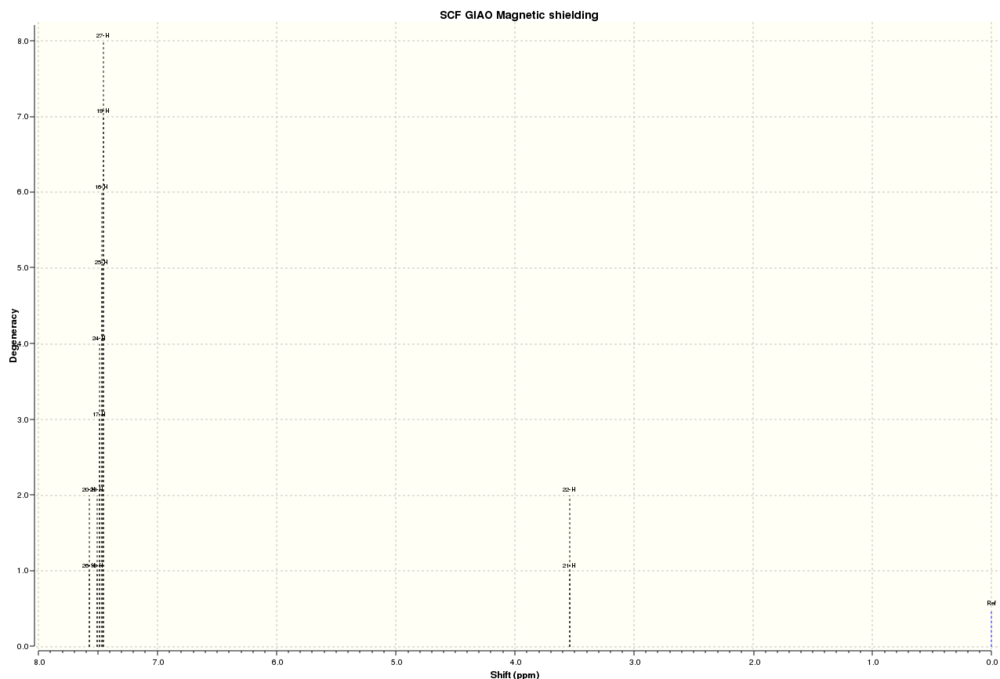
| Atoms | Computed Chemical Shifts (ppm) | Literature Chemical Shifts (ppm)[10] |
|---|---|---|
| 26, 20 | 7.57 | 7.30 - 7.38 |
| 18, 23, 17, 24, 25, 16, 19, 27 | 7.48 | 7.30 - 7.38 |
| 21, 22 | 3.54 | 3.87 |
The chemical shifts of aromatic protons are in the expected chemical shift region and the literature values match up nicely with the computed spectrum.
13CNMR Stilbene:
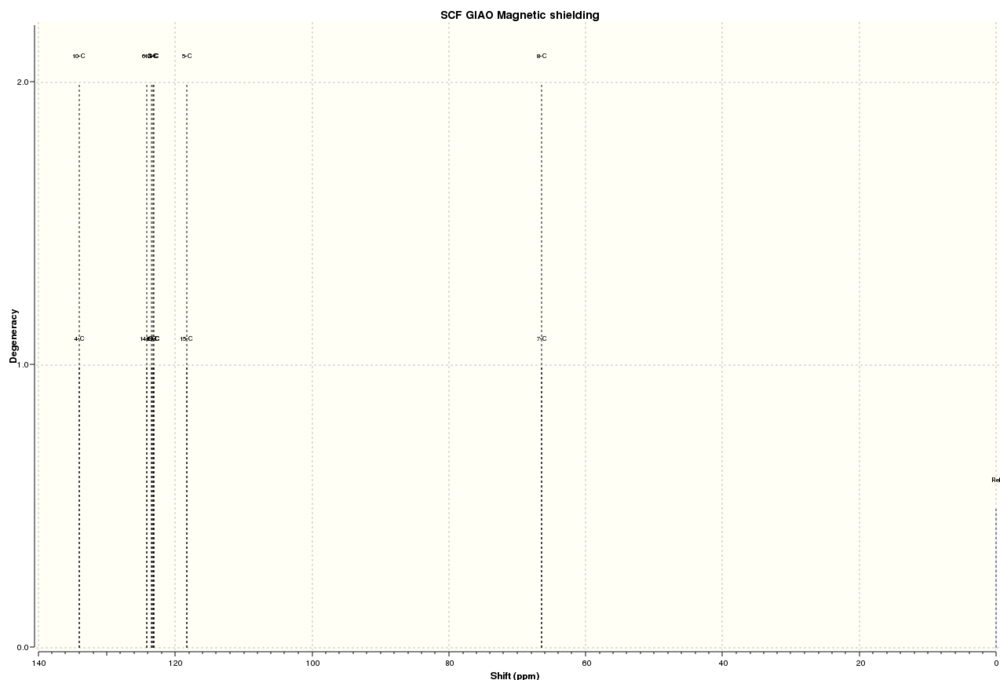
| Atoms | Computed Chemical Shifts (ppm) | Literature Chemical Shifts (ppm)[10] |
|---|---|---|
| 4, 10 | 134.09 | 137.21 |
| 14, 6 | 124.23 | 128.50 |
| 2, 12 | 123.52 | 128.50 |
| 13, 1 | 123.21 | 128.30 |
| 11, 3 | 123.08 | 125.50 |
| 15, 5 | 118.26 | 125.50 |
| 7, 8 | 66.42 | 62.80 |
The paired degeneracy of the computed chemical shifts above reflects the C2 nature of trans-stilbene oxide. The computed spectrum again matches up to the literature values.
Chiroptical Properties of Epoxides: Trans-Stilbene Oxide and Dihydronaphthalene Oxide
Below are the computed chiroptical properties compared to the literature values. Gaussian calculates two different optical rotations at two different wavelengths (365 nm and 589 nm). However, the literature values were only found for optical rotations at 589 nm.
| Wavelength (nm) | Calculated Optical Rotation | Literature Optical Rotation |
|---|---|---|
| 589 | 297.88 | 296 |
| 365 | 1253.34 | - |
| Wavelength (nm) | Calculated Optical Rotation | Literature Optical Rotation |
|---|---|---|
| 589 | 149.34 | 145 |
| 365 | 932.64 | - |
The agreement from the literature that is available is very good.
Transition State Analysis Shi Catalyst
The free energies of the epoxidation transition states were computed and used to determine the enantioselectivity of each epoxidation for the Shi catalyst and the Jacobsen catalyst.
Trans-Stilbene Shi Catalyst Epoxidation
- Under kinetic control, the epoxidations of trans-stilbene and 1,2-dihydronaphthalene will proceed via the lowest energy transition state. From the computed free energies of the transition state we can deduce which stereoisomer will be produced in enantiomeric excess. The computed free energies are shown above in Hartrees/Particle.
| [R,R] Trans-Stilbene | [S,S] Trans-Stilbene |
|---|---|
| -1534.687808 | -1534.683440 |
| -1534.687252 | -1534.685089 |
| -1534.700037 | -1534.693818 |
| -1534.699901 | -1534.691858 |
The difference between the two lowest free energy transition states for both the [R,R] and [S,S] was calculated which gave 0.003812H. This was then converted into kJ/mol: 9.9112 kJ/mol, and substituted into the following equation to find K, the equilibrium constant:
ΔG = -RTlnK
K = 0.996
This value of K was then substituted into the following equation to find x, where x = enantiomeric excess:
x = K/(K+1)
x = 0.498 = 50% enantiomeric excess of [R,R] Trans-stilbene oxide.
1,2-dihydronaphthalene Shi Catalyst Epoxidation
| [R,S] Dihydronaphthalene | [S,R] Dihydronaphthalene |
|---|---|
| -1381.120782 | -1381.131343 |
| -1381.125886 | -1381.116109 |
| -1381.134059 | -1381.126039 |
| -1381.126722 | -1381.136239 |
The difference between the two lowest free energy transition states for both the [R,S] and [S,R] was calculated which gave 0.004673H. This was then converted into kJ/mol: 12.1498 kJ/mol, and substituted into the following equation to find K, the equilibrium constant:
ΔG = -RTlnK
K = 0.995
This value of K was then substituted into the following equation to find x, where x = enantiomeric excess:
x = K/(K+1)
x = 0.499 = 50% enantiomeric excess of [R,S] dihydronaphthalene oxide.
From this transition state analysis, we can analyse the mechanism of the epoxidation. It is known that the mechanism of epoxidation with dioxiranes occurs via a concerted oxygen transfer (as is further proved in the QTAIM analysis below) via a spiro aligned transition state[13]. As the catalyst approaches the alkene, the dioxirane is perpendicular to the plane of the alkene. Despite the steric repulsions that result from the planar transition state it is the main pathway that the reaction takes. The spiro transition state allows us to deduce the stereochemical outcome of the epoxidation[14].
Transition State Analysis Jacobsen's Catalyst
Cis-β-methyl styrene Jacobsen's Catalyst Epoxidation
| [S,R] cis-β-methyl styrene | [R,S] cis-β-methyl styrene |
|---|---|
| -3383.259559 | -3383.251060 |
| -3383.253442 | -3383.250270 |
The difference between the two lowest free energy transition states for both the [S,R] and [R,S] was calculated which gave 0.003172H. This was then converted into kJ/mol: 8.2472 kJ/mol, and substituted into the following equation to find K, the equilibrium constant:
ΔG = -RTlnK
K = 0.997
This value of K was then substituted into the following equation to find x, where x = enantiomeric excess:
x = K/(K+1)
x = 0.499 = 50% enantiomeric excess of [S,R] cis-β-methyl styrene oxide.
Trans-β-methyl styrene Jacobsen's Catalyst Epoxidation
| [S,S] trans-β-methyl styrene | [R,R] trans-β-methyl styrene |
|---|---|
| -3383.262481 | -3383.253816 |
| -3383.257847 | -3383.254344 |
The difference between the two lowest free energy transition states for both the [S,S] and [R,R] was calculated which gave 0.004031H. This was then converted into kJ/mol: 10.4806 kJ/mol, and substituted into the following equation to find K, the equilibrium constant:
ΔG = -RTlnK
K = 0.996
This value of K was then substituted into the following equation to find x, where x = enantiomeric excess:
x = K/(K+1)
x = 0.499 = 50% enantiomeric excess of [S,S] trans-β-methyl styrene oxide.
Styrene Jacobsen's Catalyst Epoxidation
| [S] styrene | [R] styrene |
|---|---|
| -3343.969197 | -3343.960889 |
| -3343.963191 | -3343.962162 |
The difference between the two lowest free energy transition states for both the [S] and [R] was calculated which gave 0.002302H. This was then converted into kJ/mol: 5.9852 kJ/mol, and substituted into the following equation to find K, the equilibrium constant:
ΔG = -RTlnK
K = 0.998
This value of K was then substituted into the following equation to find x, where x = enantiomeric excess:
x = K/(K+1)
x = 0.499 = 50% enantiomeric excess of [S] styrene oxide.
The transition state geometry for the Jacobsen catalysed epoxidation is slightly different. The mechanism involves a stepwise addition via radical intermediates, c.f. Shi catalysed epoxidation via dioxirane intermediate and concerted addition of oxygen. It has been suggested that there are different approaches of the catalyst for cis-substituted alkenes and trans-substituted alkenes [15]. Approach of the alkene in either a skewed or parallel orientation to the plane of the salen ligand. The epoxidation of trans-stilbene results in two competing transition state geometries[15]:
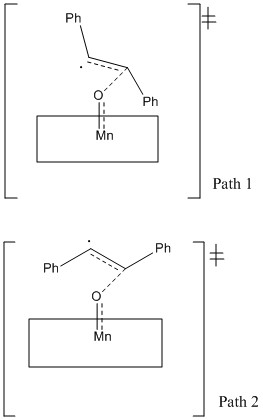
Path 1 dominates slightly because there is less steric repulsion between the alkene and ligand than in path 2. The relatively low enantioselectivity of the epoxidation of trans-stilbene using the Jacobsen catalyst can be rationalised by these two competing pathways.
Non-covalent Interactions in the Active-Site of the Reaction Transition State
Orbital |
Above is an image of the lowest energy transition state for the asymmetric Shi epoxidation of trans-stilbene. It has been subjected to a non-covalent analysis. Non-covalent interactions include van der Waals interactions, hydrogen bonding, dispersion interactions and electrostatic interactions. These images help to identify which regions of the transition state the catalyst and substrate are interacting. The colours shown in the image give an idea as to whether these interactions are attractive or repulsive (blue is strongly attractive, green is mildly attractive, yellow is mildly repulsive and red is strongly repulsive). From all this information we can deduce the stereoselectivity of the catalyst for the substrate.
The image is mainly made up of green regions suggesting mildly attractive interactions which can be interpreted using the sum of the van der Waals radii. The sum of the van der Waals radii is the length between two atoms that produces the most attractive interaction. The most interesting part of this image however is the core of the reaction centre, that being the approach of the oxygen atom towards the double bond. It has regions of blue in it suggesting strongly attractive forces. This is due to the favourable donation of a lone pair of electrons from the oxygen atom into the alkene antibonding orbital that results in a new stabilised molecular orbital. However, there are also regions of red in the same region suggesting strongly repulsive forces. This can be explained by the fact that the oxygen atom needs to approach the double bond quite close before it can donate its electrons to maximise effective orbital overlap, resulting in repulsive van der Waals interactions as the distance between atoms becomes shorter than the sum of the atomic radii. However, the attractive blue overcomes this repulsive steric interaction and goes on to form the products.
It is interesting to note that the approach of the methyl groups on the Shi catalyst towards the alkene result in green attractive interactions. It is expected that there would be some sort of steric clash of the hydrogens from the methyl groups on the catalyst with the aromatic hydrogens of trans-stilbene, however this is not the case. Again, this can be rationalised by the sum of the atomic radii being the optimum distance between these groups of atoms and the overall attractive effect of the formation of a newly stabilised MO compensating for any steric clashing.
Investigating the Electronic Topology (QTAIM) in the Active-Site of the Reaction Transition State
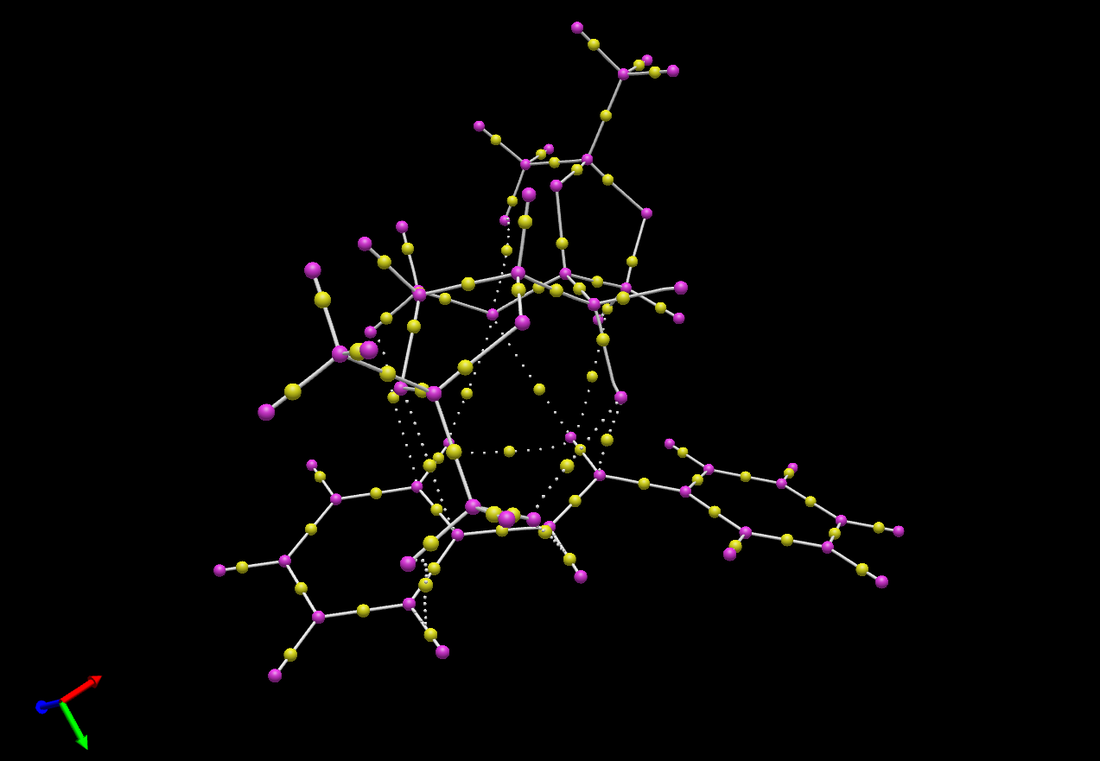
Contrary to the NCI analysis the QTAIM analysis focuses on covalent interactions, i.e. bonding interactions, as well as non-covalent interactions. A QTAIM analysis was carried out for the transition state of the asymmetric Shi epoxidation of trans-stilbene. The image above shows regions of electron density where the yellow dots indicate electron density of a bond and purple dots indicate atoms.
It is interesting to note that the approach of the oxygen towards the double bond shows a covalent interaction forming between oxygen and the double bond but also that there is still regions of electron density between the oxygen and carbon atom of the catalyst suggesting that the C-O bond has not broken completely while it forms a new covalent bond to the alkene. So, from this we can deduce that these two bond forming and bond breaking actions are concerted.
There are regions of electron density between the substrate and catalyst which hold the transition state in place to react as the positive nuclei of the alkene and catalyst are simultaneously attracted to this region of electron density thereby lowering the energy of the transition state.
Suggesting new candidates for investigations
The following compound, pulegone oxide, has an optical rotary power of 853.9 degrees at 324 nm[16]:
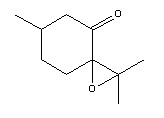
A literature reference was found on the synthesis of the above compund via the epoxidation of a double bond from the following starting material[17]:
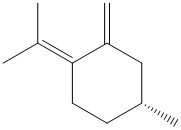
The synthesis does not require a catalyst but the reaction conditions of H2O2 and NaOH in MeOH.
References
- ↑ Jensen, F. (2007). Introduction to Computational Chemistry (2nd ed., p. 22). John Wiley and Sons.
- ↑ Jensen, F. (2007). Introduction to Computational Chemistry (2nd ed., p. 70). John Wiley and Sons.
- ↑ Caramella, P., Quadrelli, P., & Toma, L. (2002). An unexpected bispericyclic transition structure leading to 4+2 and 2+4 cycloadducts in the endo dimerization of cyclopentadiene. Journal of the American Chemical Society, 124(7), 1130-1.DOI:10.1021/ja016622h
- ↑ W. F. Maier, P. Von Rague Schleyer, J. Am. Chem. Soc., 1981, 103, 1891.DOI:10.1021/ja00398a003
- ↑ L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, J. Am. Chem. Soc.,, 1990, 112, 277-283. DOI:10.1021/ja00157a043
- ↑ http://www.gaussian.com/g_whitepap/nmrcomp.htm. Date Accessed: 27/11/2013
- ↑ Zhi-Xian Wang, S.M.Miller, O.P.Anderson, Yian Shi, J.Org.Chem., 66, 521, 2001, DOI:10.1021/jo001343i
- ↑ J.W.Yoon, T.-S.Yoon, S.W.Lee, W.Shin. , Acta Crystallogr., Sect.C:Cryst.Struct.Commun., 55, 1766, DOI:10.1107/S0108270199009397
- ↑ Mantina, M., Chamberlin, A. C., Valero, R., Cramer, C. J., & Truhlar, D. G. (2009). Consistent van der Waals radii for the whole main group. The journal of physical chemistry. A, 113(19), 5806–12.DOI:10.1021/jp8111556
- ↑ 10.0 10.1 10.2 10.3 Ji, L., Wang, Y.-N., Qian, C., & Chen, X.-Z. Nitrile-Promoted Alkene Epoxidation with Urea–Hydrogen Peroxide (UHP). Synthetic Communications, 2013, 43(16), 2256-2264. doi:10.1080/00397911.2012.699578 DOI:10.1080/00397911.2012.699578
- ↑ Diep-Vohuule, Anh; Solladie-Cavallo, Arlette; Sunjic, Vitomir; Vinkovic, Vladimir Tetrahedron Asymmetry, 1996 , vol. 7, # 6 p. 1783 - 1788, DOI:10.1016/0957-4166(96)00213-3
- ↑ Hamada; Irie; Katsuki; Sasaki; Suzuki Tetrahedron, 1994 , vol. 50, # 41 p. 11827 - 11838, DOI:10.1016/S0040-4020(01)89298-X
- ↑ Houk, K. N., Liu, J., Demello, N. C., & Condroski, K. R. Transition States of Epoxidations : Diradical Character , Spiro Geometries , Transition State Flexibility , and the Origins of Stereoselectivity. Chart, 1997, 119, 10147-10152.DOI:10.1021/ja963847x
- ↑ Wang, Z.-xian, Tu, Y., Frohn, M., Zhang, J.-rong, & Shi, Y. An Efficient Catalytic Asymmetric Epoxidation Method. Tetrahedron, 1997, 119, 11224-11235.DOI:10.1021/ja972272g
- ↑ 15.0 15.1 Brandes, B. D., & Jacobsen, E. N. Highly Enantioselective, Catalytic Epoxidation. J. Org. Chem, 1994, 59, 4378-4380.DOI:10.1021/jo00095a009
- ↑ Johnson, K. The Oxides, 1963 2557(3), 2557-2560.DOI:10.1021/jo01045a016
- ↑ Raldugin, V. A., Bagryanskaya, I. Y., Gatilov, Y. V., Edil, T. T., Turdybekov, K. M., & Adekenov, S. M. Synthesis and Crystal and Molecular Structure of a Pulegone Isoxazole Derivative. Education, 2005, 41(1), 83-84.
