Jump to content

Rep:Mod:AGB1993

From ChemWiki

Third Year Computational Chemistry Lab: Bonding and Molecular Orbitals in Main Group Compounds

Day 1

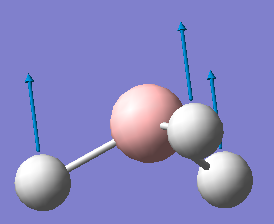
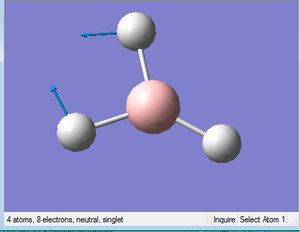
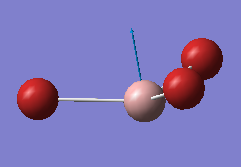
BH3 Optimization

BH3_OPT.LOG

Summary:

File Type: .log
Calculation type: FOPT
Calculation Method: RB3LYP
Basis Set: 3-21G
Final Energy: -26.462263 a.u.
Gradient: 0.00020672 a.u.
Dipole Moment: 0.00 Debye
Point Group: D3h
Calculation Time: 15 seconds


Converged Forces 

        Item               Value     Threshold  Converged?
Maximum Force            0.000413     0.000450     YES
RMS     Force            0.000271     0.000300     YES
Maximum Displacement     0.001610     0.001800     YES
RMS     Displacement     0.001054     0.001200     YES

A Better Basis Set: 6-31G(d,p)

AGB BH3 OPT 631G DP

Summary:

File Type: .log
Calculation type: FOPT
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Charge: 0
Spin: Singlet
Final Energy: -26.615324 a.u.
RMS Gradient Norm: 0.00000235 a.u.
Dipole Moment: 0.00 Debye
Point Group: D3h
Calculation Time: 4.0 seconds


Converged Forces 

        Item               Value     Threshold  Converged?
Maximum Force            0.000005     0.000450     YES
RMS     Force            0.000003     0.000300     YES
Maximum Displacement     0.000019     0.001800     YES
RMS     Displacement     0.000012     0.001200     YES

Optimised B-H bond distance and Optimised H-B-H bond angle

B-H bond distance: 1.19 Angstrom

H-B-H bond angle: 30.0 Degrees

Comparison of Total Energies for Both Basis Sets

Total Energy (3-21G): -26.462263 a.u.

Total Energy (6-31G(d,p)): -26.615324 a.u.

Day 2

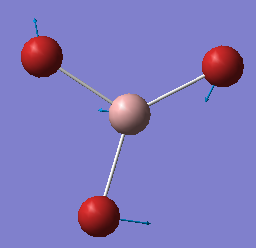
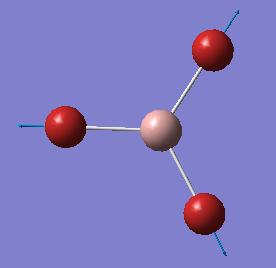
GaBr3 Optimisation

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25215

Summary:


File Type: .log
Calculation Type: FOPT
Calculation Method: RB3LYP
Basis Set: LANL2DZ
Charge: 0
Spin: Singlet
Final Energy: -41.700828 a.u.
RMS Gradient Norm: 0.00000016 a.u.
Dipole Moment: 0.00 Debye
Point Group: D3h
Calculation Time: 11.6 seconds


Converged Forces

Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000003 0.001800 YES
RMS Displacement 0.000002 0.001200 YES

Optimised Ga-Br Bond Distance and Br-Ga-Br Bond Angle

Optimised Ga-Br bond distance: 2.35 angstroms

Optimised Br-Ga-Br bond angle: 30.0 degrees

Comparison of Optimised Ga-Br Bond Distance to Literature

If we compare the obtained Ga-Br bond distance, 2.35 Å, to the literature value of 2.3525 Angstroms[1] we can see that the value obtained computationally is not unreasonable.

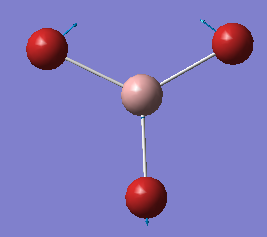
Combining Basis Sets and Pseudo Potentials: BBr3 Optimisation

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25228

Summary:


File Type: .log
Calculation Type: FOPT
Calculation Method: RB3LYP
Basis Set: GEN
Charge: 0
Spin: Singlet
Final Energy: -64.436453 a.u.
RMS Gradient Norm: 0.00000382 a.u.
Dipole Moment: 0.00 Debye
Point Group: D3h
Calculation Time: 17.0 seconds



Converged Forces

Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000023 0.001200 YES

Optimised B-Br Bond Distance and Br-B-Br Angle

Optimised B-Br bond distance: 1.93 Angstroms

Optimised Br-B-Br bond angle: 30.0 Degrees

Comparing the Bond Distances for BH3, BBr3 and GaBr3

Optimised Bond Distance (Å)
BH3 1.19
BBr3 1.93
GaBr3 2.35


- For BH3 and BBr3, both central elements are the same, but the ligands change and the bond lengths are 1.19 Å and 1.93 Å respectively. The B-Br bond length is significantly lengthened and is almost double that of the B-H bond length.

- Even though the difference in electronegativity between the boron and bromine atoms is larger than that of the boron and hydrogen atoms, the bromine atom is much larger than the hydrogen atom. This means that the internuclear distance for boron and bromine is much larger than for boron and hydrogen, leading to a longer B-Br bond. So, the size of the ligand, and not the electronegativity difference is the overriding factor.

- On changing the central element from boron to gallium, we see an increase in bond length, by comparing the B-Br (1.19 Å) bond length and Ga-Br (2.35Å) bond length.

- This is again due to the size, which overrides the effects of electronegativity. Gallium and boron are both in group 3 of the periodic table and both have fairly similar electronegativities. However, gallium is a significantly larger atom than boron and this increases the internuclear distance thereby increasing the bond length of Ga-Br compared to B-Br.

Questions

In some structures gaussview does not draw in the bonds where we expect, does this mean there is no bond? Why?

Gaussview has a certain set of criteria that decides whether two atoms are bonded by defining a specific bond lenth, over which the two atoms are not bonded. This does not therefore necessarily mean there is no bond, it just means that the bond may be weakened or stretched.

What is a bond?

A bond is an electrostatic attraction between two opposite charges, the charges being either electrons and nuclei or coming from a dipole. There are two main types of bond: covalent and ionic. In a covalent bond, the electrons are shared between the two atoms and in an ionic bond one atom accepts or donates electrons valence electrons to/from the other atom.

The maximum attraction between two atoms can be defined by the sum of the van der Waals radii for the two atoms concerned. If the distance between the two atoms is shorter than the sum of the van der Waals radii, the forces can become repulsive, and if the distance becomes much longer then the bond will eventually dissociate and there will be no attractive forces between the two atoms.

Day 3

Frequency Analysis of BH3

AGB_BH3_FREQUENCY

Summary:

File Type: .log
Calculation Type: FREQ
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Charge: 0
Spin: Singlet
Final Energy: -26.615324 a.u.
RMS Gradient Norm: 0.00000237 a.u.
Dipole Moment: 0.00 Debye
Point Group: D3h
Calculation Time: 13.0 seconds

Low Frequencies

Low Frequencies -0.9033 -0.7343 -0.0054 -6.7375 12.2491 12.2824
Low Frequencies 1163 1213 1213 2582 2715 2715




No. Form of Vibration Frequency Intensity Symmetry D3h Point Group
1
widthpx
The H atoms move up and down in a concerted bending motion, while the B atom moves in the opposite direction.		 1163 93 A2"
2
widthpx
2 H atoms move in a concerted bending motion along the molecule plane. The B atom moves in a concerted motion with the remaining H atom		 1213 14 E'
3
widthpx
All H atoms move in a concerted bending motion in opposing directions along the plane of the molecule while the B atom moves along the plane of the molecule also.		 1213 14 E'
4
widthpx
All H atoms move in and out in plane of molecule in a concerted stretching motion while the B atom stays stationary.		 2582 0 A1'
5
widthpx
Two H atoms move in and out in a stretching motion in opposing directions, while the B atom and remaining H atom move in a concerted motion.		 2715 126 E'
6
widthpx
Two H atoms move in and out in a concerted stretching motion, while the remaining H atom moves in and out in an opposing direction that is concerted with the B atom.		 2715 126 E'

IR Spectrum of BH3


Why are there less than six peaks in the spectrum, when there are obviously six vibrations?

- Vibration number 4 has an intensity of zero meaning that the peak will not show up in the spectrum. This is because the vibration is not IR-active since there is no change in the dipole moment as it vibrates.

- Vibrations 2 and 3 have very similar intensities, the same vibrational frequencies and degenerate symmetry groups meaning that the two vibrations merge into one signal.

- Vibrations 5 and 6 have the same vibrational frequencies, very similar intensities and degenerate symmetry groups meaning that the two vibrations merge into one signal.

- This leaves vibration 1 which has a different symmetry group to the rest of the vibrations, a different frequency and a different intensity meaning it gives rise to its own single peak.

- This all adds up to 3 peaks in total.

GaBr3 Frequency Analysis

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25314

Summary:

File Type: .log
Calculation Type: FREQ
Calculation Method: RB3LYP
Basis Set: LANL2DZ
Charge: 0
Spin: Singlet
Final Energy: -41.700828 a.u.
RMS Gradient Norm: 0.00000011 a.u.
Dipole Moment: 0.00 Debye
Point Group: D3h
Calculation Time: 10.4 seconds

Low Frequencies

Low frequencies --- -0.5252, -0.5247, -0.0024, -0.0010, 0.0235, 1.2010

Low frequencies --- 76, 76, 100, 197, 316, 316


Lowest Real Normal Mode: 76

IR Spectrum of GaBr3

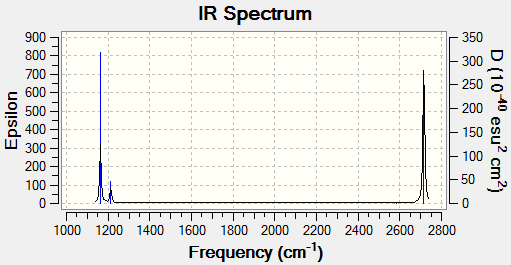
Comparing the Frequencies

No Form of Vibration Frequency Intensity Symmetry D3h Point Group
1
widthpx
Br-Ga-Br group move in a concerted bending motion as the remaining H atom moves in the opposite direction.		 76 3 E'
2
widthpx
Ga-Br unit moves up and down in a bending motion and remaining Br atoms move up and down in a concerted bending motion.		 76 3 E'
3
widthpx
3 Br atoms move up and down in a concerted bending motion while the Ga atom moves in the opposite direction.		 100 9 A2"
4
widthpx
3 Br atoms move in and out in a concerted stretching motion while the Ga atom is stationary		 197 0 A1'
5
widthpx
One Br atom is stationary, while the Br-Ga-Br group moves in an asymmetric stretch.		 316 57 E'
6
widthpx
A Br-Ga unit moves in a two-atom stretch and the Br-Ga-Br unit moves in a symmetric stretch.		 316 57 E'


Table of Frequencies For GaBr3 and BH3:

Molecule 1 2 3 4 5 6
GaBr3 76 76 100 197 316 316
BH3 1163 1213 1213 2582 2715 2715

What does the large difference in the value of the frequencies for BH3 compared to GaBr3 indicate?

This indicates the difference in size of the atoms between the two molecules, since vibrational frequency depends on the reduced mass from the equation:

widthpx


Since it is an inverse relationship, the vibrational frequencies of GaBr3 are smaller, since the ligands and central element are much heavier than for BH3.[2]

Has there been a reordering of modes?

Yes there has been a reordering of modes since the A2" mode has been reordered from the first mode in BH3 to the 3rd mode in GaBr3 which also results in a reordering of the first two E' modes.

How are these spectra similar?

They both have 3 visible peaks.

For both spectra two modes lie fairly closely together, the A2 and E' modes and then the other two modes also lie fairly close together, the A1' and E' modes, but higher in energy. Why is this?

The A2 and E' modes are both bending modes and therefore, for both spectra, the vibrational frequencies for these symmetry groups are similar. The A1' and E' modes are both stretching modes and for both spectra these frequencies are therefore similar. The A1' and E' modes are higher in energy because stretching vibrations generally require more energy than bending vibrations and therefore result in higher frequencies for the A1' and E' modes compared to the A2 and E' modes.

Why must you use the same method and basis set for both the optimisation and frequency analysis calculations?

To ensure that the final energies are the same and therefore that we are dealing with two of the same structures.

What is the purpose of carrying out a frequency analysis?

To ensure that our structures are indeed minimums.

What do the "Low frequencies" represent?

The first low frequencies row represents the motions of the center of mass of the molecule. These are much smaller than the second row which lists the vibrations of the molecule corresponding to each symmetry group.

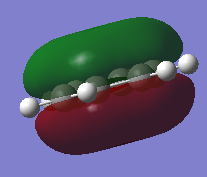
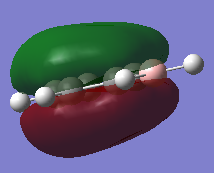
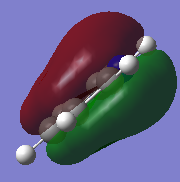
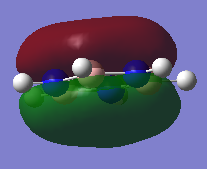
Molecular Orbitals of BH3

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25322

Summary:

File Type:.chk
Calculation Type: SP
Calculation Method: RB3LYP
Basis Set: 6-31G(D,P)
Charge: 0
Spin: Singlet
Final Energy: -26.615324 a.u.
RMS Gradient Norm: 0.000 a.u.
Dipole Moment: 0.00 Debye

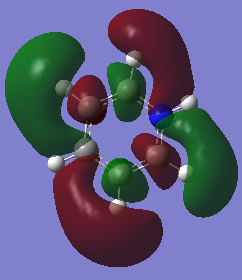
Molecular Orbital Diagram of BH3


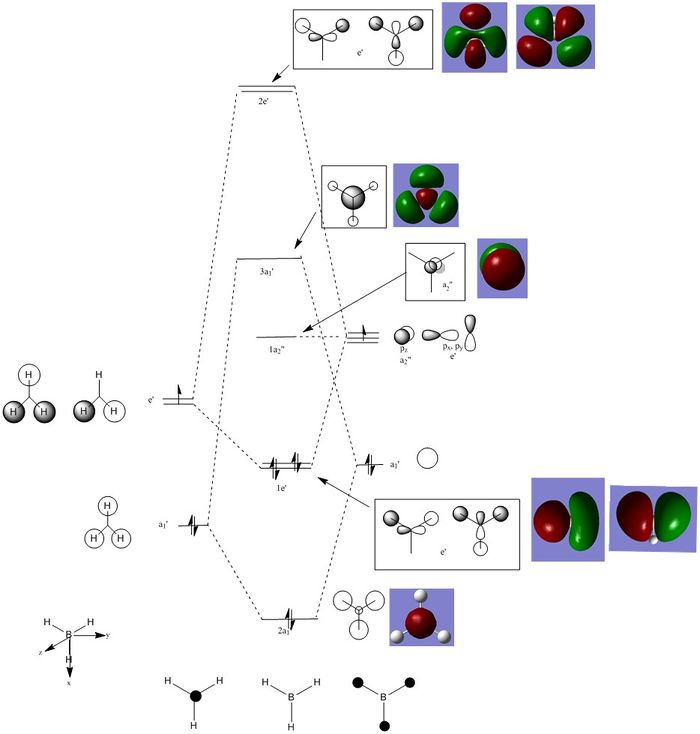
Are there any significant differences between the real and LCAO MOs?

- The s-p overlap in the LCAO compared to the real MOs is different, with the real MO showing the s and p orbitals joined into one new molecular orbital.

- For the 2a1 level, the LCAO shows the s orbitals on the hydrogens and boron to be separate, whereas the real MO shows the completely bonded s orbitals of the hydrogens and boron as one fully bonding MO that is centered at the boron atom.

What does this say about the accuracy and usefulness of qualitative MO theory?

It is very useful as a starting point, however, knowledge of how atomic orbitals interact with each other and form new molecular orbitals is necessary to be able to fully analyse the molecular orbitals of a particular molecule.

NH3 Optimisation

AGB_NH3_DP_OPTIMISATION

Summary:

File Type: .log
Calculation Type: FOPT
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Charge: 0
Spin: Singlet
Final Energy: -56.557769 a.u.
RMS Gradient Norm: 0.00000885 a.u.
Dipole Moment: 1.85 Debye
Point Group: C1
Calculation Time: 10.0 seconds.

N.B. Even though the point group in the summary says C1, the real point group for NH3 is C3v.

Converged Forces

Item Value Threshold Converged?
Maximum Force 0.000024 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000079 0.001800 YES
RMS Displacement 0.000053 0.001200 YES

Optimised Bond Distances and Angles

Optimised N-H Bond Distance = 1.02 Angstroms

Optimised H-N-H Bond Angle = 37.1 Degrees

NH3 Frequency Analysis

Summary of further optimisation of NH3 before frequency analysis using keyword: int=ultrafine scf=conver=9

NH3_Second_optimisation_AGB

Summary:

File Type: .log
Calculation Type: FOPT
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Charge: 0
Spin: Singlet
Final Energy: -56.557769 a.u.
RMS Gradient Norm: 0.00000815 a.u.
Dipole Moment: 1.85 Debye
Point Group: C1
Calculation Time: 6.0 seconds.

Proof of Convergence

Item Value Threshold Converged?
Maximum Force 0.000003 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000007 0.001800 YES
RMS Displacement 0.000003 0.001200 YES

Link to Frequency Calculation:

NH3_frequency_AGB

Summary of Frequency Calculation:

File Type: .log
Calculation Type: FREQ
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Charge: 0
Spin: Singlet
Final Energy: -56.557769 a.u.
RMS Gradient Norm: 0.00000891 a.u.
Dipole Moment: 1.84 Debye
Point Group: C1
Calculation Time: 8.0 seconds.

Proof of Minimisation by Low Frequencies

Low frequencies --- -9.2109 -8.1223 -6.2020 0.0006 0.0009 0.0015

Low frequencies --- 1089, 1694, 1694, 3461, 3590, 3590

Molecular Orbitals of NH3

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25340

Summary of MO Analysis

File Type: .log
Calculation Type: SP
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Charge: 0
Spin: Singlet
Final Energy: -56.557769 a.u.
Dipole Moment: 1.84 Debye
Point Group: C1
Calculation Time: 7.5 seconds.

NH3 NBO Analysis

Charge Distribution

widthpx

Range: -1.0 to 1.0

Specific NBO charge for nitrogen: -1.125

Specific NBO charge for hydrogen: 0.375

NH3BH3 Optimisation

Link:

AGB_NH3BH3_OPTIMISATION

Summary:

File Type: .log
Calculation Type: FOPT
Calculation Method: UB3LYP
Basis Set: 6-31G(d,p)
Charge: 0
Spin: Doublet
Final Energy: -82.549442 a.u.
RMS Gradient Norm: 0.00000051 a.u.
Dipole Moment: 5.63 Debye
Point Group: C1
Calculation Time: 46.0 seconds.

Converged Forces:

Item Value Threshold Converged?
Maximum Force 0.000002 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000016 0.000060 YES
RMS Displacement 0.000007 0.000040 YES

NH3BH3 Frequency Analysis

Link:

AGB_FREQUENCY_NH3BH3

Summary:

File Type: .log
Calculation Type: FREQ
Calculation Method: UB3LYP
Basis Set: 6-31G(d,p)
Charge: 0
Spin: Doublet
Final Energy: -82.549442 a.u.
RMS Gradient Norm: 0.00000054 a.u.
Dipole Moment: 5.63 Debye
Point Group: C1
Calculation Time: 39.0 seconds.

Converged Forces:

Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000015 0.001800 YES
RMS Displacement 0.000008 0.001200 YES

Proof of Minimum by Low Frequencies:

Low frequencies --- -8.8480, 0.0004, 0.0008, 0.0009, 0.2526, 6.4603

Low frequencies --- 239, 594, 651, 686, 877, 1059

Calculation of Association Energies

Molecule Final Energy (a.u.)
NH3 -56.557769
BH3 -26.615324
NH3BH3 -82.549442


Energy Difference:

ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]

= 0.624 a.u.

Dissociation Energy/Bond Energy: 

 = 1621.49 kJ/mol



  1. ↑ Lide, David R, "CRC Handbook of Chemistry and Physics", '2013-2014, 94, 1399.
  2. ↑ Jensen, Frank, "Introduction to Computational Chemistry", '2007, 2, 432.

Week 2 - Mini Project - Aromaticity

Week 2 - Benzene

Benzene Optimisation (6-31G Basis Set)

Dspace:

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25474

Summary:

File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Charge = 0
Spin = Singlet
E(RB3LYP) = -232.258206 a.u.
RMS Gradient Norm = 0.00009550 a.u.
Dipole Moment = 0.0001 Debye
Point Group = C1
Calculation time: 57.4 seconds.

Item Table: 

 Item Value Threshold Converged?
Maximum Force 0.000212 0.000450 YES
RMS Force 0.000085 0.000300 YES
Maximum Displacement 0.000991 0.001800 YES
RMS Displacement 0.000315 0.001200 YES

Benzene Frequency Analysis

Dspace:

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25564

Summary:

File Type = .log
Calculation Type = FREQ
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Charge = 0
Spin = Singlet
E(RB3LYP) = -232.258206 a.u.
RMS Gradient Norm = 0.00009558 a.u.
Dipole Moment = 0.0001 Debye
Point Group = C1
Calculation time = 47.6 seconds.

Converged Forces: 

 Item Value Threshold Converged?
Maximum Force 0.000190 0.000450 YES
RMS Force 0.000093 0.000300 YES
Maximum Displacement 0.000971 0.001800 YES
RMS Displacement 0.000372 0.001200 YES

Low Frequencies and no negative frequencies:

Low frequencies --- -15.5056 -14.4335 -13.9326 -0.0007 -0.0003 0.0007

Low frequencies --- 414.0670, 414.1475, 620.9628, 620.9704, 693.0526, 718.3053, 864.1034, 864.1758, 973.6436, 973.7258, 1012.3706, 1017.8803, 1019.9460, 1066.3449, 1066.4246, 1179.2543, 1202.1725, 1202.2788, 1356.0857, 1380.2376, 1524.3490, 1524.4327, 1653.0250, 1653.1537, 3174.3425, 3183.8169, 3183.9959, 3199.4787, 3199.6573, 3210.1520

Spectrum:

Benzene Population Analysis

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25483

Benzene NBO Analysis

Charge Distribution:

widthpx

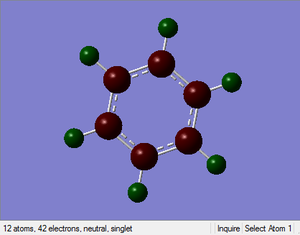
Range: -1.00 to 1.00

Specific NBO Charges:

widthpx

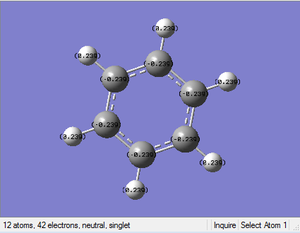
Specific NBO Charge Carbon: -0.239

Specific NBO Charge Hydrogen: +0.239

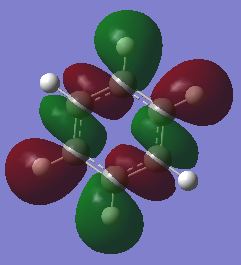
Benzene Molecular Orbital Diagram

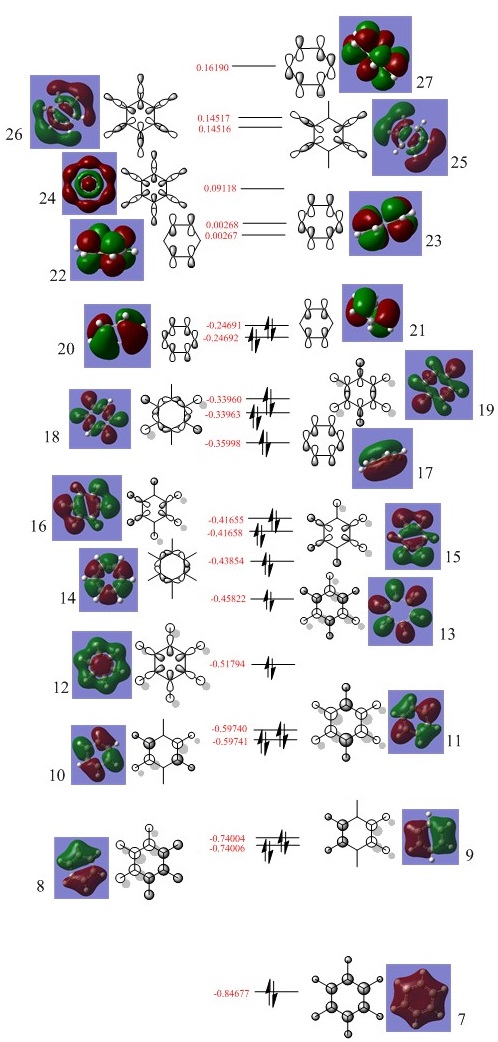
How do these MOs relate to the common conception of aromaticity?

Aromaticity is the idea that, electrons that normally occupy orbitals in pairs, are now delocalised in an electron cloud. In benzene specifically the electrons are delocalised in a cloud above and below the plane of the molecule. LCAO theory shows the electrons occupying very specific locations within s or p orbitals, whereas the MOs computed by Gaussian show a more delocalised and spread out view of the orbitals. In addition, the p orbital overlap that forms a pi bond is difficult to represent using drawn molecular orbitals, but these MOs computed by Gaussian show the pi bonds that form, as the p orbitals lose their typical shape and form a cloud or ring type structure above and below the plane of the molecule. This helps to relate it to the theory of aromaticity.

Week 2 - Boratabenzene

Boratabenzene Optimisation

Dspace:

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25501

Summary:

File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Charge = -1
Spin = Singlet
E(RB3LYP) = -219.020530 a.u.
RMS Gradient Norm = 0.00015822 a.u.
Dipole Moment = 2.8465 Debye
Point Group = C1
Calculation time: 28.0 seconds.

Converged Forces: 

 Item Value Threshold Converged?
Maximum Force 0.000159 0.000450 YES
RMS Force 0.000069 0.000300 YES
Maximum Displacement 0.000911 0.001800 YES
RMS Displacement 0.000335 0.001200 YES

Boratabenzene Frequency

Dspace

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25576

Summary

File Type = .log
Calculation Type = FREQ
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Charge = -1
Spin = Singlet
E(RB3LYP) = -219.020522 a.u.
RMS Gradient Norm = 0.00015676 a.u.
Dipole Moment = 2.8467 Debye
Point Group = C1
Calculation time: 58.2 seconds.

Low Frequencies and No Negative Frequencies

Low frequencies --- -6.8488 -0.0001 0.0005 0.0009 3.2602 5.6229

Low frequencies --- 371.2616, 404.4992, 565.1641, 568.3301, 608.0689, 710.7277, 756.6598, 814.9152, 873.5246,906.3515, 917.4298, 950.7178, 951.3335, 960.3054, 1012.1150, 1084.9956, 1175.2468, 1179.7598, 1227.9104, 1333.5285, 1449.2578, 1462.8113, 1564.5869, 1591.5283, 2446.6005, 3027.4802, 3029.5284, 3059.6215, 3060.7453, 3115.0029

Converged Forces 

 Item Value Threshold Converged?
Maximum Force 0.000439 0.000450 YES
RMS Force 0.000157 0.000300 YES
Maximum Displacement 0.000855 0.001800 YES
RMS Displacement 0.000392 0.001200 YES

Boratabenzene Population Analysis

Dspace

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25650

Summary:

File Type = .fch
Calculation Type = SP
Calculation Method = RB3LYP
Basis Set = 6-31G(D,P)
Charge = -1
Spin = Singlet
Total Energy = -219.020530 a.u.
RMS Gradient Norm = 0.00000000 a.u.
Dipole Moment = 2.8465 Debye

Boratabenzene NBO Analysis

Charge Distribution

widthpx

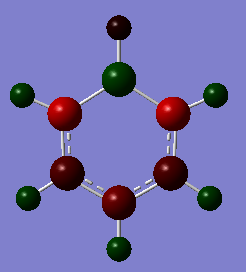
Range: -1.00 - 1.00

Specific NBO Charges

widthpx
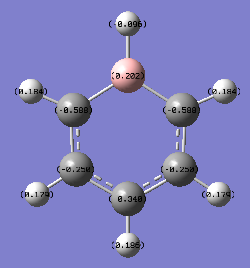
Atom Specific NBO Charge
Hydrogen para to boron +0.186
hydrogen meta to boron +0.179
hydrogen ortho to boron +0.184
carbon para to boron -0.340
carbon meta to boron -0.250
carbon ortho to boron -0.588
boron +0.202
hydrogen bonded to boron -0.096

Week 2 - Pyridinium

Pyridinium Optimisation

Dspace

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25657

Summary


File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Charge = 1
Spin = Singlet
E(RB3LYP) = -248.668074 a.u.
RMS Gradient Norm = 0.00003896 a.u.
Dipole Moment = 1.8727 Debye
Point Group = C1
Calculation time: 21.2 seconds.


Converged Forces 

 Item Value Threshold Converged?
Maximum Force 0.000064 0.000450 YES
RMS Force 0.000023 0.000300 YES
Maximum Displacement 0.000702 0.001800 YES
RMS Displacement 0.000174 0.001200 YES

Pyridinium Frequency Analysis

Dspace:

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25674

Summary

File Type = .log
Calculation Type = FREQ
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Charge = 1
Spin = Singlet
E(RB3LYP) = -248.668061 a.u.
RMS Gradient Norm = 0.00003256 a.u.
Dipole Moment = 1.8727 Debye
Point Group = C1
Calculation time: 36.9 seconds.

Converged Forces 

 Item Value Threshold Converged?
Maximum Force 0.000128 0.000450 YES
RMS Force 0.000033 0.000300 YES
Maximum Displacement 0.000790 0.001800 YES
RMS Displacement 0.000228 0.001200 YES

Low Frequencies and No Negative Frequencies

Low frequencies --- -9.4924, -5.2498, -0.0009, -0.0007, 0.0006, 4.0077

Low frequencies --- 391.9056, 404.3502, 620.1994, 645.1608, 676.7768, 747.7032, 854.2647, 882.7249 991.9079 1005.6392 1022.4651 1047.8035 1052.1362 1082.1541 1087.1614 1199.6044, 1228.7653, 1299.8972, 1374.0760, 1416.0790, 1523.6838, 1580.1828, 1656.6983, 1676.5303, 3223.6622, 3240.2767, 3241.8120, 3252.4512, 3253.8171, 3569.2668

Pyridinium Population Analysis

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25677

Summary:

File Type = .fch
Calculation Type = SP
Calculation Method = RB3LYP
Basis Set = 6-31G(D,P)
Charge = 1
Spin = Singlet
Total Energy = -248.668074a.u.
RMS Gradient Norm = 0.00000000 a.u.
Dipole Moment = 1.8728 Debye

Pyridinium NBO Analysis

Charge Distribution:

widthpx

Range: -1.00 to 1.00

Specific NBO Charges:

widthpx
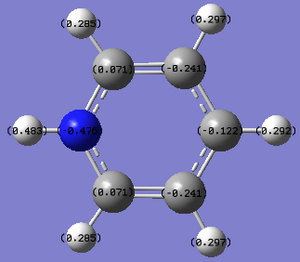
Atom Specific NBO Charge
hydrogen ortho to nitrogen +0.285
hydrogen meta to nitrogen +0.297
hydrogen para to nitrogen +0.292
carbon ortho to nitrogen +0.071
carbon meta to nitrogen -0.241
carbon para to nitrogen -0.122
nitrogen -0.476
hydrogen bonded to nitrogen +0.483

Week 2 - Borazine

Borazine Optimisation

Dspace:

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25565

Summary:

File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Charge = 0
Spin = Singlet
E(RB3LYP) = -242.684598 a.u.
RMS Gradient Norm = 0.00007126 a.u.
Dipole Moment = 0.0003 Debye
Point Group = C1
Calculation time: 21.2 seconds.

Converged Forces 

Item Value Threshold Converged?
Maximum Force 0.000117 0.000450 YES
RMS Force 0.000036 0.000300 YES
Maximum Displacement 0.000327 0.001800 YES
RMS Displacement 0.000104 0.001200 YES

Borazine Frequency Analysis

Dspace

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25584

Summary

File Type = .log
Calculation Type = FREQ
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Charge = 0
Spin = Singlet
E(RB3LYP) = -242.684600 a.u.
RMS Gradient Norm = 0.00006962 a.u.
Dipole Moment = 0.0002 Debye
Point Group = C1
Calculation time: 11 minutes 0.1 seconds.

Low Frequencies and No Negative Frequencies

Low frequencies --- -3.7898 -0.0004 0.0009 0.0010 0.4352 6.8161

Low frequencies --- 289.6164, 289.6921, 404.1981, 525.0377, 525.0434, 710.0461, 710.1329, 732.3031, 864.4660, 927.4413, 927.4548, 936.8217, 944.4549, 944.5425, 944.9663, 1051.7880, 1080.5904, 1080.6761, 1245.3291, 1314.0322, 1400.0665, 1400.1590, 1492.1887, 1492.2960, 2641.5556, 2641.6181, 2651.5003, 3642.1285, 3643.9256, 3643.9833

Converged Forces 

 Item Value Threshold Converged?
Maximum Force 0.000205 0.000450 YES
RMS Force 0.000070 0.000300 YES
Maximum Displacement 0.000369 0.001800 YES
RMS Displacement 0.000133 0.001200 YES

Borazine Population Analysis

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/25652

Borazine NBO Analysis

Charge Distribution

widthpx

Range: -1.00 to 1.00

Specific NBO Charges

widthpx
Atom Specific NBO Charge
Nitrogen -1.102
Boron +0.747
hydrogen bonded to nitrogen +0.432
hydrogen bonded to boron -0.077

Week 2 - Comparison of Charge Distributions

Charges Across the Atoms in this Series of Molecules
Molecule 1 2 3 4 5 6 7 8 9 10 11 12
Benzene -0.239 -0.239 -0.239 -0.239 -0.239 -0.239 +0.239 +0.239 +0.239 +0.239 +0.239 +0.239
Boratabenzene +0.202 -0.588 -0.250 -0.340 -0.250 -0.588 -0.096 +0.184 +0.179 +0.186 +0.179 +0.184
Pyridinium -0.476 +0.071 -0.241 -0.122 -0.241 +0.071 +0.483 +0.285 +0.297 +0.292 +0.297 +0.285
Borazine -1.102 +0.747 -1.102 +0.747 -1.102 +0.747 +0.432 -0.077 +0.432 -0.077 +0.432 -0.077

- The electronegativities of boron, carbon and nitrogen are 2.01, 2.50 and 3.07 respectively[1].

- The benzene framework is made up of only carbons and is negatively charged because carbon is more electronegative than hydrogen.

- If we compare boratabenzene and benzene, the carbons ortho to the boron atom in boratabenzene are more negatively charged than those in benzene because the electron withdrawing effect of boron is not as strong as that of carbon. This makes the whole carbon framework more negatively charged in boratabenzene than in benzene, with the effect being more pronounced in the carbons ortho to the boron and less so in the carbon para to the boron atom. The hydrogen atoms in boratabenzene (excluding the one directly bonded to boron)are more negatively charged than in benzene which is again due to the same effect of the boron atom being less electron withdrawing than carbon, resulting in more electron density on the hydrogens in boratabenzene than in benzene. For the hydrogen atom that is bonded directly to the boron atom, it is much more negatively charged than the corresponding atom in benzene. This is because boron is less electronegative than carbon, leaving more electron density on the hydrogen in boratabenzene. The boron atom itself is more positive than the corresponding carbon atom in benzene because carbon is more electronegative than boron.

- Comparing benzene and pyridinium, the carbon framework of pyridinium is more positive than in benzene because the nitrogen is more electronegative than carbon and withdraws electron density from the carbon framework, making it more positively charged. The carbon framework of pyridinium is also more positively charged than in boratabenzene, because nitrogen is more electronegative than boron. Nitrogen itself is highly negatively charged due to its high electronegativity. The hydrogens are also more positively charged than those in boratabenzene and in benzene, which is again due to the high electronegativity of nitrogen.

- Borazine's framework is made up of both boron and nitrogen. Since nitrogen is more electronegative than boron, the nitrogens are more negatively charged than the boron atoms. The hydrogens bonded to nitrogens are more positively charged than those bonded to boron atoms, since nitrogen withdraws more electron density than boron. The nitrogen atoms in borazine are more negative than the nitrogen atom in pyridinium because, in borazine the nitrogens are bonded to boron atoms, whereas in pyridinium the nitrogen is bonded to two carbon atoms. Since carbon atoms are more electronegative than boron atoms, they withdraw more electron density resulting in a more positive nitrogen atom in pyridinium than in borazine.

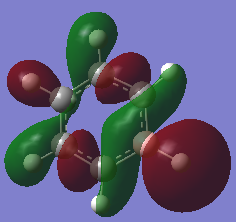
Week 2 - Comparison of MOs

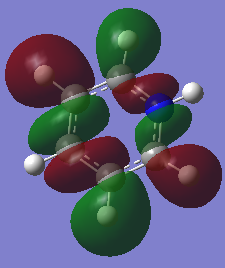
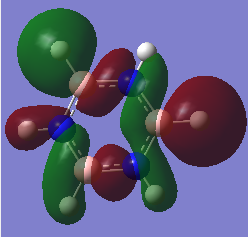
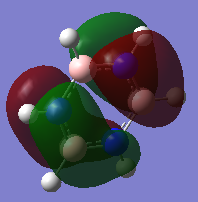
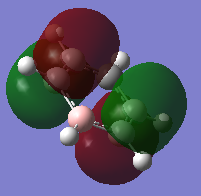
Orbital 17

Molecule Molecular Orbital Energy Electron Density
Benzene
widthpx
 -0.35998 These MOs are all bonding in character. In benzene, the pi orbitals that form two rings above and below the benzene ring have an even electron density over the carbon framework. Comparing this to the corresponding molecular orbital in boratabenzene, we can see that since boron is less electronegative than carbon, the ring electron density gets smaller over the boron atom. In contrast, the corresponding pyridinium molecular orbital has more electron density over the nitrogen atom, since nitrogen is more electronegative than carbon.
Boratabenzene
widthpx
 -0.13208 As already mentioned, the electron density gets smaller over the boron atom. This means that the energy of the molecular orbital is higher than that of benzene.
Pyridinium
widthpx
 -0.64064 The effect of electronegativity is particularly visible in this molecular orbital. It is clear that the electron density increases over and below the nitrogen atom. This results in a decrease and stabilisation of this molecular orbital energy compared to the corresponding benzene and boratabenzene molecular orbitals (energy of pyridinium MO is almost double that of benzene MO, disregarding the signs).
Borazine
widthpx
 -0.36130 The energy of the borazine MO is similar to that of the benzene MO, and the MO looks similar too, with an even distribution of electron density over and above the ring. This is due to a combination of the stronger electron withdrawing effect of nitrogen than carbon, and the weaker electron withdrawing effect of boron than carbon. This then results in a very similar electron density above and below the ring to that of benzene.

Orbital 18

Molecule Molecular Orbital Energy Analysis
Benzene
widthpx
 -0.33963 All of these MOs are antibonding in character. They are all made up of LCAOs that are made up of p orbitals only, however the p orbitals form no pi bonds like in orbital 17. The energies can be rationalised similarly to the energies of orbitals 17. This benzene MO has a similar energy to that of borazine. The borazine MO has the two opposing effects of nitrogen being strongly electron withdrawing and boron being weakly electron withdrawing, compared to carbon. Since borazine contains equal numbers of nitrogen atoms and boron atoms, its energy is similar to that of benzene, whose framework is made up of only carbons. This is because their electron densities are similar.
Boratabenzene
widthpx
 -0.09171 Boratabenzene has the highest energy of all the MOs because the boron atom is weakly electron withdrawing compared to carbon and nitrogen, contributing to a higher energy.
Pyridinium
widthpx
 -0.57741 Pyridinium has the lowest energy MO since nitrogen is highly electron withdrawing compared to carbon and boron and withdraws more electron density over the nitorgen atom contributing to a lower energy.
Borazine
widthpx
 -0.31996 Borazine has a similar energy to that of benzene as explained in the benzene analysis box.

Highest Occupied Molecular Orbital

Molecule Molecular Orbital Energy Analysis
Borazine
widthpx
 -0.27590 The MOs across this series of molecules has been ordered in increasing energy. All the MOs are antibonding in character, their LCAOs are all made up of only p orbitals, however their energies differ. This borazine MO has the lowest energy and is therefore the most stable in energy. This is because the pi bond formed over and above the ring is spread across a larger section of the ring compared with benzene and boratabenzene for example.
Benzene
widthpx
 -0.24691 This benzene MO is visually very similar to the corresponding HOMO in boratabenzene. This also means that their energies are similar. They both form pi bonds between two atoms on either side of the rings. The energies of boratabenzene and benzene are both higher than that of borazine because the two pi bonds in borazine form over the 3 atoms each compared to just two atoms each in benzene and boratabenzene.
Boratabenzene
widthpx
 -0.03493 The energy of this boratabenzene MO is slightly higher than the corresponding HOMO in benzene because the boron is less electronegative than carbon, and this reduces the electron density over the boron atom, increasing the energy of the MO. Even though there is no p orbital over the boron atom, this still has a very small effect on the electron density and energy, because there are no other differences in the molecular orbital of boratabenzene compared to benzene.
Pyridinium
widthpx
 -0.00495 This pyridinium MO looks visually very different to the other MOs. This is because there are no pi bonds forming. However, the LCAO is similar since the MO is made up of only p orbitals. It is antibonding in character just as the other MOs. Since pyridinium contains a nitrogen atom, which is more electronegative than carbon and boron, we would expect that the electron density over this atom is greater contributing to a smaller energy compared to the other MOs. However, this is not the case due to there being no pi bonding, which stabilises the MO contributing to a smaller energy in borazine, benzene and boratabenzene.

Effect of Substitutions on Full MO Diagram

Boratabenzene

Boratabenzene would have the effect of raising the energies of the MOs in general compared to the benzene MO, since the boron atom substituion makes the energies of the MOs higher because boron is less electronegative than carbon.

Pyridinium

Pyridinium would have the effect lowering the energies of the MOs in general compared to the benzene MO diagram, since nitrogen is more electronegative than carbon.

Borazine

Borazine has boron and nitrogen atoms substituted in place of the carbon framework in benzene. The combined result of the relatively strong electron withdrawing effects of nitrogen atoms and the relatively weak electron withdrawing effects of the boron atoms is that the MO diagram is similar to that of benzene, with regards to the MO energies. The LCAO will differ slightly due to the differing atoms, but the energy levels of the MOs produced from the LCAOs will be similar to that of benzene.


  1. ↑ Zhang, Yonghe, "American Chemical Society, Electronegativities of Elements in Valence States", '1982, 82, 3888.
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:AGB1993&oldid=816177"