Rep:Mod:AC5116
2nd Year Inorganic Computational Chemistry Lab - Day 1: Optimisation of EX3 Species
BH3 Frequency Calculations
Method, Basis set and Results
BH3 was initially optimised using the B3LYP method with a 3-21G basis set. The structure was then optimised again using the B3LYP DFT functional with a 6-31G(d,p) basis set, then optimised at this level again and symmetrised into the D3h point group. Frequency calculations were then calculated on the optimised structure at the B3LYP/6-31G(d,p) level.
B3LYP/6-31G(d,p) Level

Item Table
Item Value Threshold Converged? Maximum Force 0.000014 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000056 0.001800 YES RMS Displacement 0.000037 0.001200 YES
The 'item' table of the final optimised structure indicates that the optimisation has converged correctly.
Low Frequencies:
Low frequencies --- -15.9409 -15.9378 -12.6652 0.0006 0.0143 0.3146 Low frequencies --- 1162.9369 1213.1137 1213.1139
The first 6 of these frequencies correspond with translations and rotations of the molecule and are ideally equal to 0. These values are all significantly different to the next 3 low frequencies, corresponding to actual normal modes of vibration, and hence are acceptable
The *.log file for the frequency calculation can be found here: AC5116_BH3_FREQ.log.
BH3 Optimised with 6-31G(d,p) Basis |
Vibrational Spectrum of BH3
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1163 | 93 | A2 | yes | out-of-plane bend |
| 1213 | 14 | E' | very slight | bend |
| 1213 | 14 | E' | very slight | bend |
| 2583 | 0 | A1' | no | symmetric stretch |
| 2716 | 126 | E | yes | asymmetric stretch |
| 2716 | 126 | E | yes | asymmetric stretch |

Despite there being 6 normal vibrational modes of BH3 only 3 peaks apperar in the predicted spectrum. There are 2 pairs of degenerate vibrational modes with symmetry E'(1213 cm-1 and 2716 cm-1, hence 4 modes result in only two peaks and one of the other two modes is IR inactive (2583 cm-1). The IR inactive mode is so because it involves the totally symmetric stretching of all 3 B-H bonds and a zero transitional dipole moment.
The Molecular Orbitals of BH3
The optimisation of BH3 with the 6-31G(d,p) basis set gives rise to 30 MOs. This is considerably more than in the typical qualitative MO picture, which only has 8 MOs because qualitative MO diagrams always use a minimal basis set, whereas the 6-31G(d,p) has split valence orbitals (2 orbitals per normal minimal basis valence atomic orbital) and added d polarisation functions on the boron atom and p polarisation functions on the hydrogen atoms.
Of the 30 computed MOs, the lowest 4 are occupied. The figure below shows a qualitative MO diagram of BH3 along with the first 8 computed MOs of BH3.
As can be seen above, the simple qualitative MOs correspond quite closely to the computed MOs, showing the strength of Qualitative MO theory. Some of the computed MOs, however, have a few odd differences between them and the qualitative pictures. For example, the 3a1' orbitals shown look very similar from the front, however, the side on view of the calculated MO shows a large red lobe that has an oddly cylindrically shape that protrudes out from the plane of the molecule, whereas this is expected to be spherical by qualitative MO theory.

Smf115 (talk) 23:57, 21 May 2018 (BST)Well presented MO diagram and nice inclusion of the 3a1' MO to illustrate the subtle differences between the qualitative LCAO approach and the calculated MOs. The opening paragraph raises a good idea, however, isn't fully correct. For example, there are only 8 MOs in the qualitative MO diagram because we only choose to consider that many. The LCAO approach can be applied to generate higher MOs but as these are non-bonding, high energy MOs then they are not of interest to us.
Determining H3B-NH3 Adduct Bond Strength
The dissociation energy of a Lewis Base-Lewis Acid adduct can be calculated as the energy of the adduct relative to the total energies of the two separate molecules: ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]. Performing this calculation is acceptable provided the same level of theory is used for the optimisations and energy calculations of each of the 3 molecules. The energy of BH3 from the optimisation described above shall be used, along with the energies from B3LYP/6-31G(d,p) optimisations of NH3 and the H3B-NH3 adduct.
Smf115 (talk) 23:51, 21 May 2018 (BST)Nice introduction to the section showing understanding of the limitations to comparing calculations.
NH3 Optimisation
Optimisation Calculation was carried out on NH3 at the B3LYP/6-31G(d,p) theory level.

The item table found in the *.log file shows that the optimisation converged. Further frequency calculations showed no negative frequencies, indicating a minimum was found successfully.
Item Table
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES RMS Displacement 0.000037 0.001200 YES
The *.log file for this optimisation calculation can be found here: Media:AC5116 NH3 OPT B3LYP 631G D P.LOG.
The low frequencies table of the frequency log file had:
Low frequencies --- -0.0138 -0.0032 -0.0015 7.0783 8.0932 8.0937 Low frequencies --- 1089.3840 1693.9368 1693.9368
The energy of the optimised NH3 molecule is: E(NH3)=-56.55777 Hatrees (5.d.p)
NH3 Optimised with 6-31G(d,p) Basis |
BH3NH3 Complex Frequency Optimisation
Frequency-Optimisation Calculation was carried out on BH3NH3 at the B3LYP/6-31G(d,p) theory level. and symmetrised to the C3v point group.

The item table found in the *.log file shows that the optimisation converged. Further frequency calculations showed no negative frequencies, indicating a minimum was found successfully.
Item Table
Item Value Threshold Converged? Maximum Force 0.000123 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000585 0.001800 YES RMS Displacement 0.000320 0.001200 YES
The *.log file for this frequency-optimisation calculation can be found here: Media:AC5116 BH3NH3 OPT FREQ B3LYP 631G D P.LOG.
The low frequencies table of the frequency log file had:
Low frequencies --- 0.0008 0.0008 0.0010 16.8436 17.4462 37.3291 Low frequencies --- 265.8243 632.2043 639.3227
The energy of the optimised BH3NH3 molecule is: E(BH3NH3)=-83.22469 Hatrees (5.d.p)
The frequency analysis showed no negative frequencies; minimum found.
BH3NH3 Optimised with 6-31G(d,p) Basis |
Calculating the association energy of NH3 and BH3, ΔE
Using the energies of the individual molecules and the complex:
E(BH3)=-26.61532 Hatrees (5.d.p)
E(NH3)=-56.55777 Hatrees (5.d.p)
E(BH3NH3)=-83.22469 Hatrees (5.d.p)
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] using the conversion 1 kJmol-1 = 0.0004
ΔE=-129 kJmol-1
BBr3 Optimisation
An optimisation calculation was carried out on BBr3 with mixed basis sets (LanL2DZ for Br and 6-31G(d,p) for B) theory level using the B3LYP DFT Functional. A LanL2DZ pseudo-potential was used on the Br atoms. This pseudo replaces several core electrons on all 3 Br atoms with a potential function that are easier to calculate. This has the effect of decreasing computational time as the use of fewer orbitals on Br reduces the size of the matrices of orbitals used during energy calculations.

The item table found in the optimisation *.log file shows that the optimisation converged. Further frequency calculations showed no negative frequencies, indicating a minimum was found successfully.
Item Table
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000024 0.001200 YES
The *.log file for this optimisation calculation can be found here: Media:AC5116 BBR3 OPT B3LYP 631G D P LANL2DZ.LOG. The *.log file of the frequency calculation was uploaded to the DSpace repository DOI:10042/202388 .
The low frequencies table of the frequency log file had:
Low frequencies --- -2.3055 -0.0029 -0.0018 0.0774 0.7534 0.7534 Low frequencies --- 155.9402 155.9405 267.6894
The frequency analysis showed no negative frequencies; minimum found.
BH3NH3 Optimised with 6-31G(d,p) Basis |
2nd Year Inorganic Computational Chemistry Lab - Day 2 and 3: Project - Aluminium trihalides as Lewis Acids and Bases
Aluminium trihalides, as monomers, contain a central aluminium atom bonded to 3 electron withdrawing halide groups. This makes the aluminium atom extremely electron deficient, allowing to function as a Lewis Acid. Unlike in boron trihalides, aluminium trihalides don't exist as monomers as the Al 3p orbitals are too large for effective pi overlap for stabilisation by hyperconjugation, as in BX3, so instead must dimerise, usually understood as by donation of a lone pair from a halogen on one AlX3 monomer to the empty Al 3p of another. The dimer formed is stable relative to the separated molecules due to these interactions.
Smf115 (talk) 23:50, 21 May 2018 (BST)Great introduction to the project section with clear thought given to the system being studied.

Of course, under MO theory, orbitals are delocalised across the molecule and include contributions from multiple atoms, so this simple picture doesn't necessarily hold true.
In the following project the 2 isomers of the (AlCl2Br)2 dimer are calculated and discussed. They are highlighted in the diagram below, out of 3 other isomers of this dimer.

Optimisation of the AlCl2Br Monomer, Isomer 1 and Isomer 2
All 3 molecules were optimised using B3LYP with the 6-31G(d,p)/LanL2DZ mixed basis. The LanL2DZ basis and pseudo potential were used on Br atoms and the 6-31G(d,p) basis set on Cl and Al atoms. All were optimised into their correct point groups.
The summary tables of all 3 optimisations are below.


The item tables all showed convergence and the low frequencies showed no large transnational/rotational frequencies:
Monomer: Freq log file: Media:AC5116 ALBRCL2 MONOMER FREQ B3LYP 631G D P LANLDZ.LOG
Item Value Threshold Converged? Maximum Force 0.000092 0.000450 YES RMS Force 0.000045 0.000300 YES Maximum Displacement 0.001710 0.001800 YES RMS Displacement 0.001067 0.001200 YES
Low frequencies --- 0.0025 0.0029 0.0031 3.3756 3.6552 4.1209 Low frequencies --- 120.7185 133.9343 185.8750
Isomer 1: Freq log file: Media:AC5116 AL2BR2CL4 TRANS CLBRIDGE FREQ.LOG
Item Value Threshold Converged? Maximum Force 0.000056 0.000450 YES RMS Force 0.000029 0.000300 YES Maximum Displacement 0.000966 0.001800 YES RMS Displacement 0.000305 0.001200 YES
Low frequencies --- -1.2316 -0.9577 0.0023 0.0024 0.0027 2.9388 Low frequencies --- 18.3248 49.2664 72.8875Isomer 2:
Opt log file: Media:AC5116_AL2BR2CL4_BR_BRIDGE_FREQ_D2H_631G_D_P_LANLDZ.LOG
Maximum Force 0.000118 0.000450 YES RMS Force 0.000046 0.000300 YES Maximum Displacement 0.001337 0.001800 YES RMS Displacement 0.000537 0.001200 YES
Low frequencies --- -2.3824 0.0024 0.0025 0.0028 0.0337 1.1622 Low frequencies --- 15.9625 63.4410 85.9623
- Frequency calculations on Isomer 1 and 2 broke convergence somehow. I realised this just before initially submitting and attempted to recalculate both frequency files. The MOs in the later section are from the original frequency calculation of the trans Cl bridged isomer.*
J mol:
Monomer |
Isomer 1 |
Isomer 2 |
Relative energies=
E(Monomer) = -1176.19014 au E(Isomer 1) = -2352.41630 au E(Isomer 2) = -2352.40632 au
Energy of forming isomer 1 = E(Isomer 1) - 2*E(Monomer) = -90 kJmol-1
Isomer 1 is more stable as the smaller 3p orbitals on Cl overlap better with the 3p on Al giving stronger donation.
MOs of Isomer 1
The 4 MOs of Isomer 1 are analysed below.

This MO is a strongly anti-bonding unoccupied, where this filled it is unlikely any Al-Cl-Al bridging would occur.

This occupied MO is responsible for a large amount of the Cl-Al-Cl bridging bonding. The next highest orbital has some Al-Al bonding character also responsible for bridging.
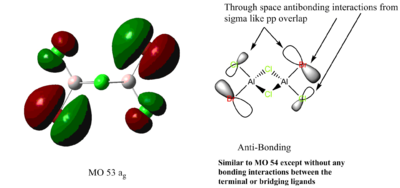
This MO is occupied and very-weakly anti-bonding(only anti-bonding interactions however all are weak due to pi like overlap of distant p orbitals.
Smf115 (talk) 23:48, 21 May 2018 (BST)Good MO analysis with a nice range of character covered by the MOs chosen. The key interactions are labelled clearly with good terminology. To develop the discussion durther more details could be included. For example, even though electron density is polarised off the terminal atoms the s-orbital contributions should be included on the LCAO for MO 57. The nodal plane close to these atoms and the medium through space interaction between the terminal s-orbitals could then be annotated too.
Smf115 (talk) 23:48, 21 May 2018 (BST)Overall a good report with obvious thought given to the project section.

