Rep:Mod:AB01346889
1st Year Modelling 2 Report
Using Gaussview, molecules were optimised and then their properties were recorded on this page, such as vibrational modes and frequencies, bond lengths, bond angles and molecular orbitals.
Part 1: Molecule optimisation
NH3
Molecule name: NH3 (ammonia)
| Calculation Method | Basis Set | Final Energy E(RB3LYP) | RMS Gradient Norm | Point Group |
|---|---|---|---|---|
| RB3LYP | 6-31G(d,p) | -56.55776873 a.u. | 0.00000485 a.u. | C3V |
Optimised bond length: 1.01798 Å
Optimised angle (HNH): 105.741o
RMS Gradient Norm 0.00000485 < 0.0005, thus we can consider that optimisation has run correctly.
| Item | Value | Threshold | Converged |
|---|---|---|---|
| Maximum Force | 0.000004 | 0.000450 | YES |
| RMS Force | 0.000004 | 0.000300 | YES |
| Maximum Displacement | 0.000072 | 0.001800 | YES |
| RMS Displacement | 0.000035 | 0.001200 | YES |
Predicted change in Energy=-5.986256D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
NH3 |
Media:NH3OPTIMISATION2_01346889.LOG
Part 2: vibrations and charges
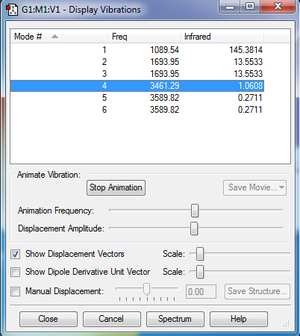
Questions
How many modes do you expect from the 3N-6 rule?
NH3 has N=4 atoms, so we expect 3*4-6=12-6=6 vibrational modes.
Which modes are degenerate (i.e. have the same energy)?
Modes 2&3 and 5&6 are degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Modes 1 to 3 are bending. Modes 4 to 6 are bond stretch.
Which mode is highly symmetric?
Mode 4 is highly symmetric.
One mode is known as the "umbrella" mode, which one is this?
Mode 1 is the umbrella mode.
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
There are four different possible energies, however mode 4 is IR inactive as there is no change in dipole moment. Thus we would expect three bands on the experimental spectrum. If we look at the theoretical spectrum we see three peaks of different intensities (the first very high, the second rather small and the last very small). What we might see on an experimental spectrum that has a lot of noise is that the last peak isn't visible and the second one might be considerably reduced.
Charges determined: -1.125 a.u. on N, 0.375 a.u. on each H
N is more electronegative than H -X(N) =3.0 and X(H)=2.2 on Pauling's scale [1]-, so the electrons shared will tend to be closer to the former rather than the latter, explaining why we would expect a slightly negative charge on N and a slightly positive charge on H.
Part 3: reactions and orbitals
N2
Molecule name: Dinitrogen (Nitrogen)
| Calculation Method | Basis Set | Final Energy E(RB3LYP) | RMS Gradient Norm | Point Group |
|---|---|---|---|---|
| RB3LYP | 6-31G(d,p) | -09.52412868 a.u. | 0.00000060 a.u. | D*H |
| Item | Value | Threshold | Converged |
|---|---|---|---|
| Maximum Force | 0.000001 | 0.000450 | YES |
| RMS Force | 0.000004 | 0.000001 | YES |
| Maximum Displacement | 0.000000 | 0.001800 | YES |
| RMS Displacement | 0.000000 | 0.001200 | YES |
Predicted change in Energy=-3.401038D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
H-H Optimised bond length: 0.74279 Å
Vibrations
Modes: 1 Freq: 2457.33 cm-1
N2 |
Media:N2OPTIMISATION1_01346889.LOG
H2
Molecule name : Dihydrogen
| Calculation Method | Basis Set | Final Energy E(RB3LYP) | RMS Gradient Norm | Point Group |
|---|---|---|---|---|
| RB3LYP | 6-31G(d,p) | -1.17853936 a.u. | 0.00000017 a.u. | D*H |
| Item | Value | Threshold | Converged |
|---|---|---|---|
| Maximum Force | 0.000000 | 0.000450 | YES |
| RMS Force | 0.000000 | 0.000300 | YES |
| Maximum Displacement | 0.000000 | 0.001800 | YES |
| RMS Displacement | 0.000001 | 0.001200 | YES |
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
H-H Optimised bond length: 0.74279 Å
Vibrations
Modes: 1 Freq: 4465.68 cm-1
H2 |
Media:H2OPTIMISATION1_01346889.LOG
Haber Process Calculations
Using the results found above we can calculate the change in energy occurring during the Haber Process for ammonia production.
E(NH3)= -56.55776873 a.u. 2*E(NH3)= 2 * -56.55776873 a.u. = -113.1155375 a.u. E(N2)= -109.52412868 a.u. E(H2)= -1.17853936 a.u. 3*E(H2)= 3 * -1.17853936 = -3.53561808 a.u. ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= 2 * -56.55776873 - (-109.52412868 + 3*-1.17853936) = -0.0557907 a.u. = -146.47849401 kJ/mol
(energy units converted using an online converter )
The energy change is negative, which means the energy of the products is smaller than that of the reactants, making the former more stable than the latter. Therefore, it is an exothermic process.
Part 4: Your choice of small molecule
CH4
Molecule Name : Methane
Optimisation
| Calculation Method | Basis Set | Final Energy E(RB3LYP) | RMS Gradient Norm | Point Group |
|---|---|---|---|---|
| RB3LYP | 6-31G(d,p) | -40.52401404 a.u. | 0.00003263 a.u. | Td |
| Item | Value | Threshold | Converged |
|---|---|---|---|
| Maximum Force | 0.000063 | 0.000450 | YES |
| RMS Force | 0.000034 | 0.000300 | YES |
| Maximum Displacement | 0.000179 | 0.001800 | YES |
| RMS Displacement | 0.000095 | 0.001200 | YES |
Predicted change in Energy=-2.256043D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.092 -DE/DX = -0.0001 !
! R2 R(1,3) 1.092 -DE/DX = -0.0001 !
! R3 R(1,4) 1.092 -DE/DX = -0.0001 !
! R4 R(1,5) 1.092 -DE/DX = -0.0001 !
! A1 A(2,1,3) 109.4712 -DE/DX = 0.0 !
! A2 A(2,1,4) 109.4712 -DE/DX = 0.0 !
! A3 A(2,1,5) 109.4712 -DE/DX = 0.0 !
! A4 A(3,1,4) 109.4712 -DE/DX = 0.0 !
! A5 A(3,1,5) 109.4712 -DE/DX = 0.0 !
! A6 A(4,1,5) 109.4712 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -120.0 -DE/DX = 0.0 !
! D2 D(2,1,5,3) 120.0 -DE/DX = 0.0 !
! D3 D(2,1,5,4) -120.0 -DE/DX = 0.0 !
! D4 D(3,1,5,4) 120.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
CH4 |
Media:CH4OPTIMISATION1_01346889.LOG
C-H Optimised Bond Length: 1.09197 Å
Comment: Stanton's work on more accurate estimates of this bond length determined C-H to be of 1.0859 ± 0.003 Å [2]
H-C-H Optimised Angle: 109.471 o
Frequency analysis
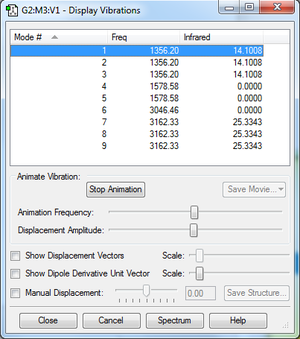
We see there are four different energy levels - modes (1,2,3), (4,5) and (7,8,9) being degenerate-, so we would expect a maximum of four bands on an experimental spectrum.
Charges
C: -0.930 a.u.
H: 0.233 a.u.
This is explained by the very small difference in electronegativities of the two atoms ( X(C)=2.6 and X(H)=2.2 on Pauling's Scale [1])
Molecular Orbitals
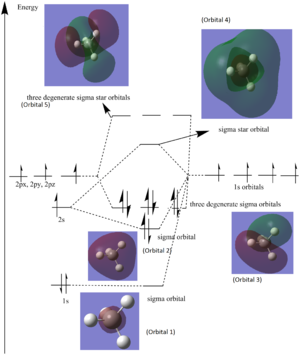
Five orbitals were chosen for the discussion: three out of the five bonding orbitals, and two anti-bonding orbitals (the LUMO and the one just after).
| Orbital 1 - MO-1 sigma | Comment |
|
Generated mainly from the 1s orbital of carbon, this orbital is very deep in energy (-10.16707 a.u.) and doesn't interact with anything, so much that its anti-bonding correspondent cannot be found (it might also be because this orbital is a mix of bonding and anti-bonding). It is an occupied molecular orbital, but doesn't lead to any bond. As the coefficient 0.99284 in the LOG file indicates, it is almost entirely comes from the 1s atomic orbital of carbon. |
| Orbital 2 - MO-2 sigma | Comment |
|
A bonding orbital. Its spherical shape and the coefficient 0.38672 in the LOG file lead us to think that the 2s atomic orbital of the carbon contributes the most to this molecular orbital. It is an occupied molecular orbital and leads to a sigma bond. It is significantly higher in energy (-0.69041 a.u.) compared to Orbital 1. |
| Orbital 3 - MO-3 sigma | Comment |
|
One of the three degenerate bonding orbitals. They look the same (same shape) but are all directed towards different axes (x, y and z). This leads us to think that there is a heavy contribution from the px, py and pz atomic orbitals of carbon respectively -in the LOG file we find the coefficient 0.44276 which supports this statement- . We note that for each orbital, hydrogens are paired up (they need to be adjacent) in a same phase. One of them (arbitrarily chosen, since the orbitals are degenerate) is the HOMO. These orbitals are occupied: lead to sigma bonding. Their energy is of -0.38831 a.u. |
| Orbital 4 - MO-6 sigma star | Comment |
|
An anti-bonding orbital. It is the LUMO: as such, it is unoccupied. By its shape, we supposed it could be the anti-bonding equivalent of Orbital 2. Its energy is of 0.11824 a.u. |
| Orbital 5 - MO-7 sigma star | Comment |
|
One of three degenerate anti-bonding orbitals. Looking at its shape, two hydrogens in the same phase at once, but this time non-adjacent hydrogens, leads us to think that these are the anti-bonding equivalent of Orbital 3 type of orbitals. The coefficients in the LOG file indicate that these orbitals come from the 2p atomic orbitals (0.38122) but from the 3p atomic orbitals as well ( 1.34476). These orbitals are higher in energy (0.17677 a.u.) and are unoccupied. |
Note: the actual electronic configuration of carbon is 1s22s22px12py1, however in the diagram an electron from 2s was promoted to 2pz, to illustrate the hybridised atomic orbitals of carbon (sp3 hybridised) and facilitate the understanding of the formation of molecular orbitals.