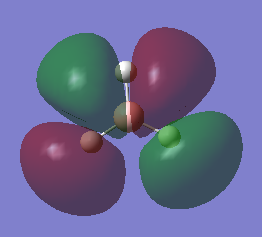Rep:Mod:A-Niall-Ator
Niall Killilea Module 2
Introduction
Chemistry, is, by its nature, an experimental nature requiring measurements of a characteristic. Computational simulation of chemical structures allows for prediction and explanation of complex systems. This module is concerned with simulation of inorganic systems and interpretation of then results.
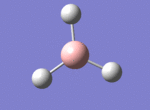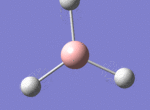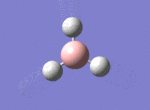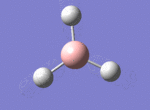
BH3
The borane BH3 is a trigonal planar, highly unstable molecule, and under ambient conditions will spontaneously dimerise to form diborane, B2H6, and only the presence of a Lewis base (for example tetrahydrofuran) wil stabilise its monomeric form. This makes studying the molecular structure of the monomeric form difficult under the best of conditions.
Computational studies of BH3 therefore allows an estimation of the molecular properties without dealing directly with the BH3.
Initial Optimisation
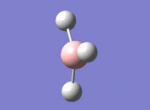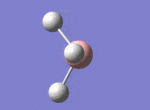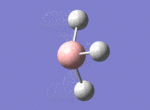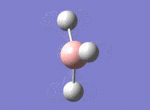
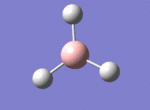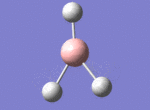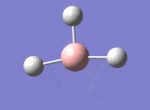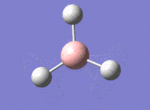
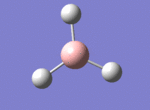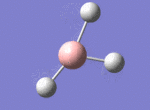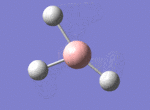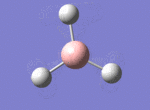
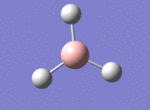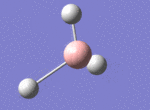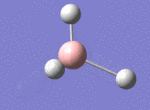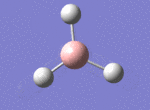
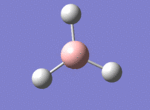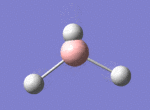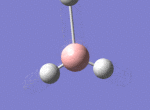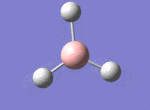
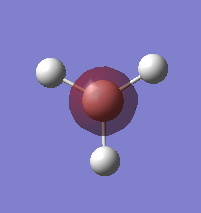
A BH3 molecule was drawn out on Gaussian. Each of the B-H bond lengths was changed to a value of 1.50Å, and the overall molecule was optimised using a B3LYP method and 3-21G basis set. The resultant molecule is as follows:
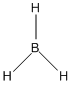
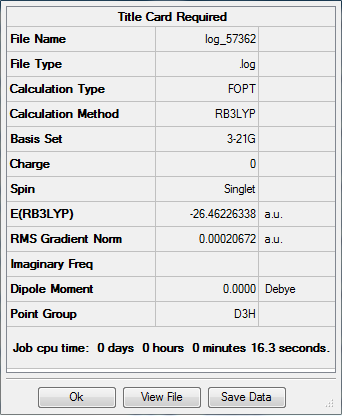
http://hdl.handle.net/10042/to-13018
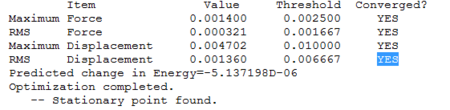
To make sure that the energy of the molecule had been minimised, the output file was opened so as to check that the calculation converged:
As shown, the potential energy of the molecule converged (ie the derivative of the potential energy dE/dx), and the minimum conformer energy was found.
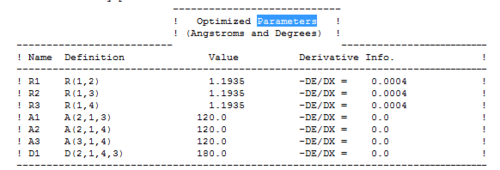
The bond angle H-B-H is 120 as expected for the D3h sp2 hybridised boron atom, and each of the B-H bond lengths is 1.194Å (see below for optimised parameters), which is in close agreement with the experimentally determined value of 1.190Å [1].
The optimisation of the molecule occurs through 4 stages:
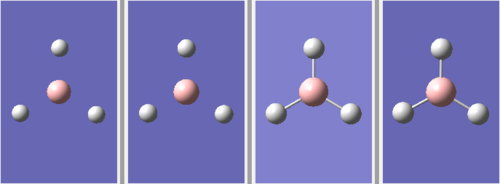
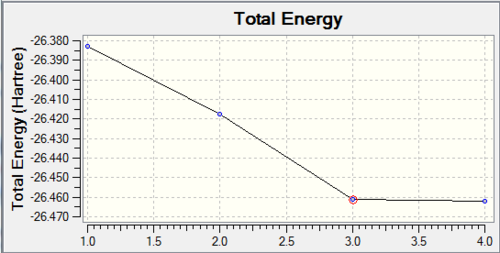
The first two stages have no formal B-H bonds. This is because the Gaussview system defines whether or not a bond exists by the distance between the atoms, rather than overlap of atomic orbitals.
The optimised parameters of the BH3 are as follows:
Vibrational Analysis
Vibrational analysis of a molecule is very important- it provides vital information concerning the strength of a bond. The summary of the BH3 vibrational analysis is as follows:
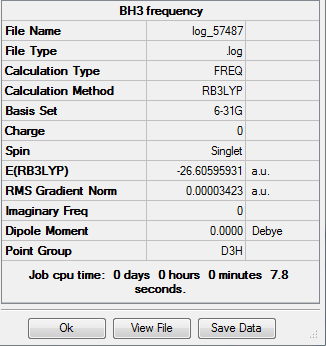
The potential energy of the molecule is very similar to that produced by the initial molecule optimisation (the two differ by a value of 0.144au)
Vibrational analysis of the BH3 molecule was carried out on the optimised BH3 molecule using the B3LYP method and 6-21G basis set. Any non-linear molecule, has 3N-6 vibrational motions, where N is the number of atoms. Therefore, in the case of BH3, there are 3(4)-6=6 vibrations:
| Molecular Vibration | Frequency (cm-1) | Intensity | Symmetry | ' |
 |
1153 | 93 | A2" | BH3 rocking |
 |
1210 | 13 | E' | BH2 scissoring |
 |
1210 | 13 | E' | BH3 wag |
 |
2576 | 0 | A1' | Symmetric B-H stretch (zero intensity due to symmetry) |
 |
2715 | 136 | E' | Assymetric B-H stretch |
 |
2715 | 136 | E' | Assymetric B-H stretch |
The overall spectrum is therefore composed of 4 peaks at 1153cm-1, 1210cm-1 and 2715cm-1. These values are within 5% of the literature values [2] of 1208cm-1, 1267cm-1 and 2791cm-1 which shows reasonable accuracy.
The “-6” vibrational motions are are motions of the centre of mass of the molecule, and are listed as "low frequencies" in the Gaussian output file. They are expected to be very small. In this case:
Another important reason for carrying out the vibrational analysis of the molecule is to ensure that the final optimised structure has been found. Consider the following sketch of the potential energy against B-H bond length:
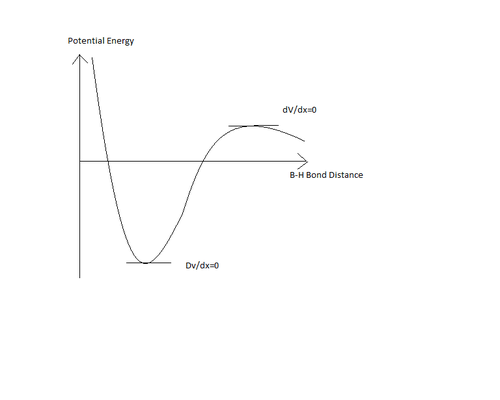
The initial optimisation carried out previously finds the optimised structure by taking a point on the potential energy curve, measuring the gradient, and changing the bond lengths and angles so as to minimise this energy until the gradient is zero. HOWEVER, the optimisation cannot differentiate between a maximum point and a minimum point on the curve, hence the optimised structure may be incorrect (resulting in a tranisiton state for the B-H bond breaking). The vibrational analysis allows for testing whether a minimum or a maximum has been found. If all of the vibrations predicted are positive, then a minimum point on the curve has been found, while if any of the vibrations are highly negative (<-10cm-1) then a maximum point on the curve has been found.
Molecular Orbitals
The energies and shape of the molecular orbitals is what dictates the reactivity of the molecule- for example, the form of the frontier molecular orbitals can explain BH3 reactivity towards Lewis Bases.
Linear combination of atomic orbitals allows for a basic representation of the BH3 molecular orbital diagram:
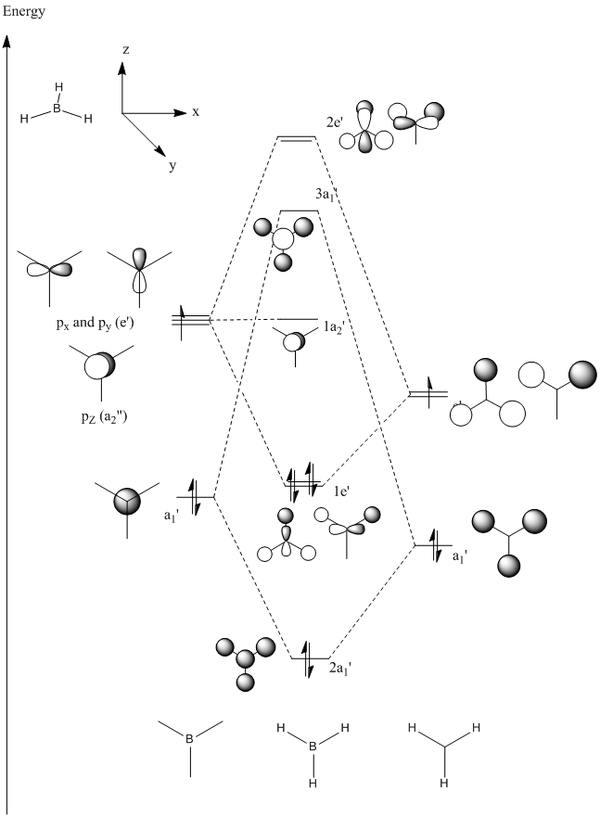
The HOMOs of the molecule is therefore the two 1e’ orbitals, and the LUMO is the 1a2’ orbital (unoccupied pz orbital).
The molecular orbitals were calculated using the DFT method and 6-21G basis set[3]. The energies and shape of the molecular orbitals is as follows:
| 1a1' | 2a1' | 1e' (HOMO) | ' |
 |
 |
 |
 |
| 1a2' (LUMO) | 3a1' | 2e' | |
 |
 |
 |
 |
As shown, the resultant MOs are of the same shape as those that resulted from the LCAO approximation.
Natural Bond Order Analysis
The natural bond analysis of the molecule is a precursor to the molecular orbital diagram. It gives important information about the molecule, including:
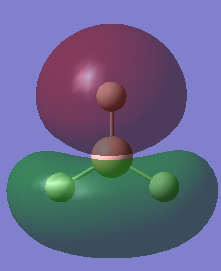
1.The distribution of the electron density:
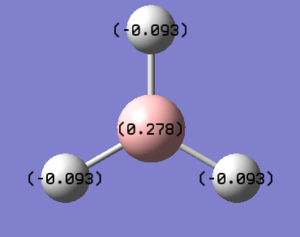
The green colour denotes a region of positive charge and the red denotes a regions of negative charge. The positive charge on the boron is expected, as the atom is a known electron acceptor (Lewis Acid).
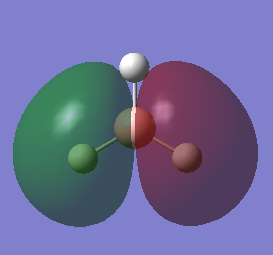
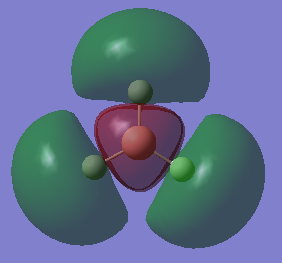
2. The breakdown of the molecular orbital- ie the atomic orbitals from each of the atoms which make up the orbital in question:
Orbitals 1; 2 and 3 are all bonding orbitals which describe the B-H bonds. Orbital 4 is the 1s non-bonding lone pair of the boron. Orbital 5 is unexpected- it predicts an s lone pair. This is probably a discrepancy in the program. Orbital 6 is the unoccupied pz orbital (LUMO). The nbo analysis shows that the 3 bonding orbitals (1, 2 and 3) is composed of 45% contribution from the boron atom- which is a 33% s orbital contribution and 67% p orbital contribution (ie. sp2)- and 55% contribution from the three hydrogen atoms.
Thallium Tribromide TlBr3
Initial Optimisation
Optimisation of TlBr3 is a great deal more complicated than for the BH3 system due to the number of electrons- the borane system only has to deal with 9 electrons while the thallium system has to deal with 186 electrons. To simplify the system, only the frontier orbitals need to be considered. For this, a different basis set is therefore required which will only consider the frontier orbitals- LANL2DZ.
The TlBr3 molecule was built on Gauassview, its symmetry restricted to D3h and the molecule optimised using the B3LYP method and LANL2DZ basis set, resulting in the following:
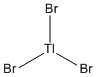
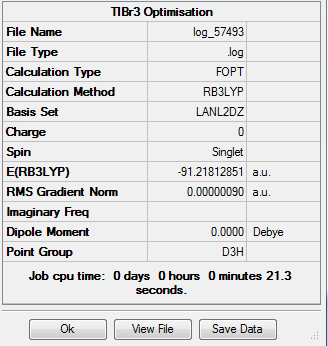
The convergence of the conformer was checked as before:
As shown, a stationary point on the potential energy curve has been found.
The optimization of the molecule occurred through three stages:
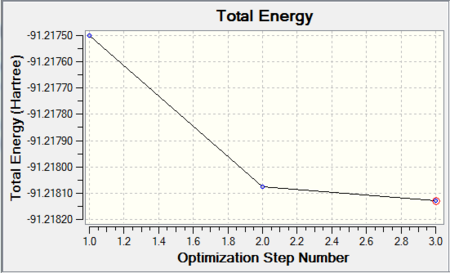
The optimized parameters of the molecule are as follows:
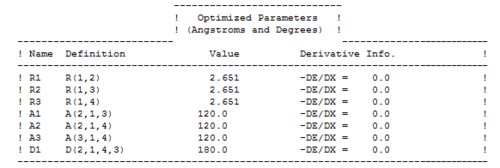
As expected for the D3h molecule, all of the bond angles are 120°. All of the bond lengths are 2.651Å, which is similar to the literature value of 2.52Å [4]. However, this literature value is measured in aqueous solvent and so is slightly different from the computed value.
Vibrational Analysis
Vibrational analysis was carried out on the molecule, again using the same B3LYP method and LANL2DZ basis set, resulting in the 6 vibrational motions as expected:
| Animation | Frequency (cm-1) | Intensity | Symmetry | Comment |
 |
46 | 4 | E' | Br-Tl-Br rocking |
 |
46 | 4 | E' | Tl-Br wagging |
 |
52 | 6 | A2" | TlBr3 deformation |
 |
165 | 0 | A1' | Tl-Br symmetric stretch (complete symmetry results in ziero intensity) |
 |
211 | 25 | E' | Assymetric Tl-Br stretch |
 |
211 | 25 | E' | Assymetric Tl-Br stretch |
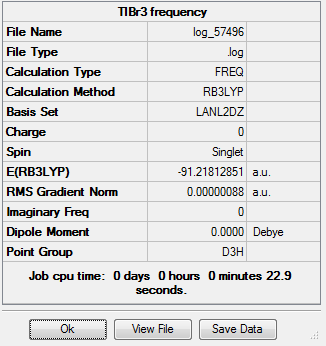
The potential energy of the molecule is identical for both the optimisation and the vibrational analysis (-91.22au). This is evidence that the optimised structure is ideal. The motions of the centre of mass of the molecule (the "-6" vibrations) are as follows:
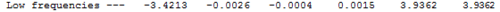
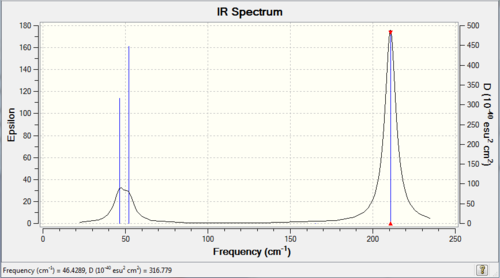
Although some of the frequencies are negative, they are all very close to zero and are therefore suitable. The overall vibrational therefore consists of 3 peaks at 46cm-1, 52cm-1 and 211cm-1. The overall spectrum is as follows:
What is A Chemical Bond?
A chemical bond can be defined as the filling of bonding molecular orbitals, a stabilising interaction of atomic orbitals between two or more atoms. Gaussview, however, only defines chemical bonds by the intermolecular distance between the atoms: if the bond distance is greater than a value defined by the program, then it will respond: no bond exists!
Molybdenum Isomers
The complex [Mo(CO)4(PCl3)2] exists as on of two possible isomers, the cis- and the trans isomer:
Due to the difference in symmetry of the two complexes, the vibrational spectra of the complexes will very different with reference to the carbonyl stretching frequencies- only one peak is observed for the trans-isomer whereas four are observed for the cis-isomer. Gaussian was used to investigate the stretching to explain this result.
Optimisation of Isomers
Consider the following potential diagram for an arbitrary molecule:
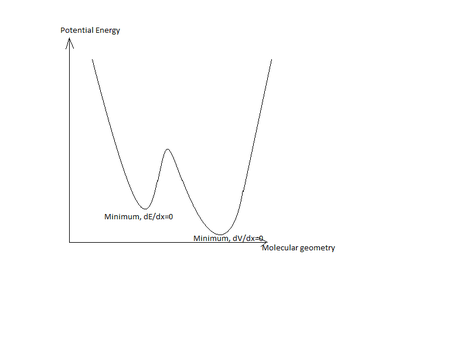
In this simplified example, there are two possible energetic minima for the molecular geometry. If the basis set is too narrow, and the calculation is started at a point closer to the higher minima than the global minima than the incorrect minima will be found. To avoid this problem, a simpler basis set must be used, and afterwards a more complicated basis set can be used to narrow down on the overall global minima.
For the two isomers of the molybdenum complex, the optimisation of each isomer was iteratively carried out three times using different basis sets:
Initial Optimisation
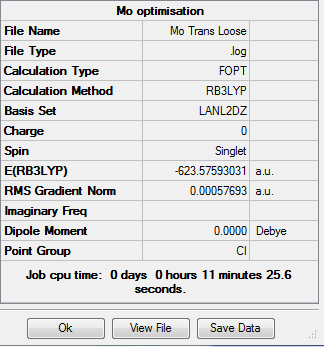
The two isomers were drawn out on Gaussian and their forms optimised using B3LYP method and LANL2DZ basis set. The additional keywords "opt=loose" were also added. The results were as follows: For the trans-isomer:
For the cis-isomer:
Convergence to a minimum was therefore successful in both cases.
Dihedral Optimisation
The two isomers were then altered before optimising the structures again.
Trans Isomer
For the trans isomer, the P-Cl bonds of the trans isomer were altered such that each P-Cl bond on either side of the Mo eclipses a P-Cl bond on the other side. The structure was then minimised using the LANL2DZ basis set, and inserted into the additional keywords is "int=ultrafine scf=conver=9" so as to ensure a more detailed basis set, resulting in the following structure:
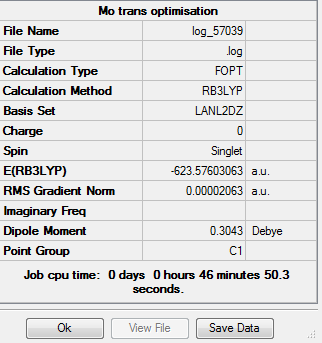
The metal-ligand bond lengths are as follows:
Where atom 1 is molybdenum, atoms 2, 4, 6 and 8 are all carbon atoms, and atoms 10 and 11 are phosphorus. The Mo-C bonds are on average 2.060Å and the Mo-P bonds are on average 2.444Å
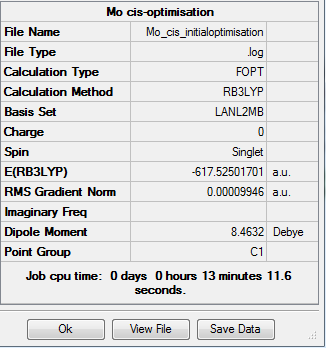
Cis-Isomer
For the cis isomer, one of the P-Cl bonds is altered on each ligand so that is lies parallel to one of the axial CO bonds. The structure was then minimised using the LANL2DZ basis set, and inserted into the additional keywords is "int=ultrafine scf=conver=9" so as to ensure a more detailed basis set, resulting in the following structure:
The metal-ligand bond lengths are as follows:
Where atom 1 is molybdenum, atoms 2, 4, 6 and 8 are all carbon atoms, and atoms 10 and 11 are phosphorus. The Mo-C bond lengths are therfore 2.012Å for the CO trans- to the phophorus ligands and 2.058Å for the CO cis- to the phosphorus.
Extra Basis Set: Introduction of D Orbitals
The third and final optimisation of the two complexes is the introduction of the low lying 3d orbitals of the phosphorus. In order to introduce these, the input file was modified with the following code at the end:
Trans-Isomer
The resultant complex for the trans-complex is as follows:
The bond lengths between the ligands and the metal are as follows:
Where atom 1 is the molybdenum, atoms 2, 4, 6 and 8 are all carbons (on the carbonyl ligands) and atoms 10 and 11 are phosphorus, ie the Mo-C bonds are all on average 2.057Å and the Mo-P bonds are both 2.422Å. The addition of the d-orbital basis set of the tow phosphorus atoms therefore results in a decrease of the Mo-P bond length from 2.44Å to 2.42Å- a very small difference, and the Mo-C bond lengths does not change (2.06Å)
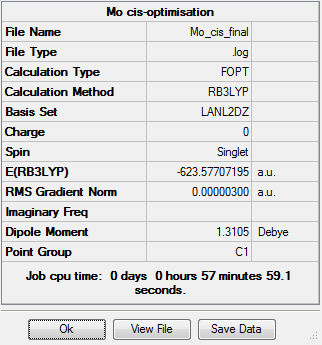
Cis-Isomer
The resultant complex for the cis-complex is as follows:
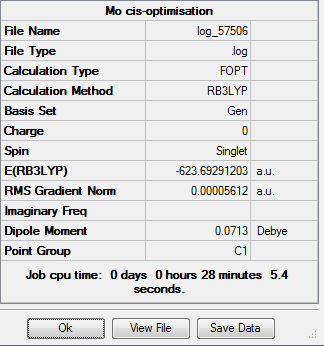
The bond lengths between the ligands and the metal are as follows:
Where atom 1 is the molybdenum, atoms 2, 4, 6 and 8 are all carbons (on the carbonyl ligands) and atoms 10 and 11 are phosphorus, ie the Mo-C bonds are 2.021Å and 2.055Å for trans- to the phosphorus and cis- to the phosphorus ligands respectively. The Mo-P bonds are both 2.476Å. The addition of the d-orbital basis set of the tow phosphorus atoms therefore results in a decrease of the Mo-P bond length from 2.50Å to 2.48Å- a very small difference, and the Mo-C bond lengths increase from 2.01Å to 2.02Å- a negligible difference.
The energy terms for the two isomers (E(RB3LYP)) shows that the two isomers are equal is stability (E(trans)=-623.7au and E(cis)=-623.7). The energies of the two comlexes can be compared to find which is more stable because they are isomers (contain the same atoms)
Vibrational Analysis
Vibrational analysis was carried out on the optimised forms of the final cis- and the trans- isomers (Including the introduction of the d orbitals of the phosphorus). The optimisation+vibrational calculation was carried out using the B3LYP method and LANL2DZ basis set with the modification of the input file to include the d orbitals.
Trans-Isomer
The summary of the vibrational analysis for the trans isomer is as follows:
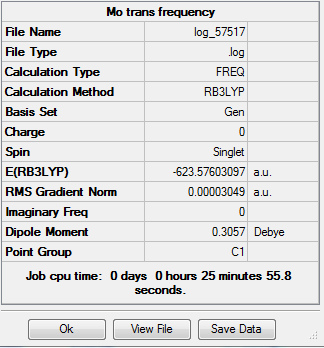
The carbonyl bond stretches are as follows:
| Animation | Frequency (cm-1) | Intensity | Comment |
 |
1950 | 1475 | |
 |
1951 | 1467 | |
 |
1977 | 0.6 | Intensity is very small due to symmetry |
 |
2031 | 4 | Intensity is very small due to symmetry |
The first two asymmetric stretches (1950cm-1 and 1951cm-1) are the only two which will appear on the vibrational spectrum, as the second two are both symmetric stretches (1977cm-1 and 2031cm-1) and have intensities of practically zero. Dynamic motion of the molecule (which is not included in this analysis) will result in the first two peaks overlapping. Computational studies of the trans isomer therefore predicts a single carbonyl stretching frequency at 1950. This result The overall vibrational spectrum of the trans-isomer is as follows:
Cis-Isomer
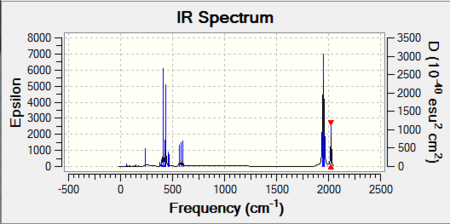
The summary of the vibrational analysis of the cis isomer is as follows:
The carbonyl bond stretches are as follows:
| Animation | Frequency (cm-1) | Intensity |
 |
1945 | 763 |
 |
1949 | 1499 |
 |
1958 | 633 |
 |
2023 | 597 |
As expected, there are four distinct carbonyl stretches all of which have a reputable intensity and would appear on the vibrational spectrum. Computational analysis therefore predicts four distinct carbonyl stretches at 1945. 1949, 1958 and 2023. This result. The overall vibrational spectrum for the cis-isomer is as follows:
Mini Project:- Variation of Organometallic Ligand Structure With Substituents
The aim of this mini-project is to investigate the structure of 3 nickel based complexes of the form trans-[Ni(CO)3(CX32] for X=Cl; Br and H and how the substituents affect the Ni-C organometallic bond length and carbonyl stretching frequencies. The bond strength of the carbonyl ligand is dependent on the the electron density of the nickel metal centre, as the backbonding of the ligand results in filling of the π* orbital and weaking of the C=O bond. Therefore, depending on the substituents of the organometallic ligand (ie X)- a strongly electronegeative atom (such as Cl) will result in less electron density on the metal and therefore a stronger C=O bond. The strength of the C=O bond for each of the complexes can be compared by comparing the symmetric C=O bond stretching frequencies.
Initial Optimisation
All three isomers were drawn out on Gaussview and optimised using the B3LYP method and 6-311G basis set, resulting in the following optimised structures:
| Complex | Summary | Structure |
| Trans-[Ni(CO)3(CBr3)2] |  |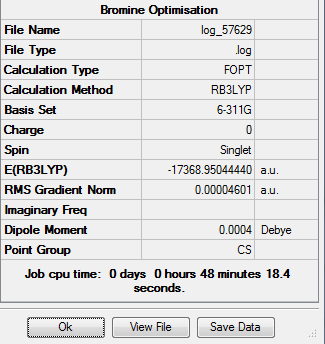
|
| Trans-[Ni(CO)3(CCl3)2] |  |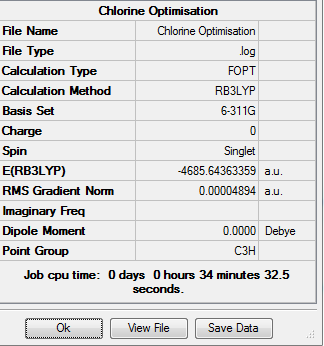
|
| Trans-[Ni(CO)3(CH3)2] |  |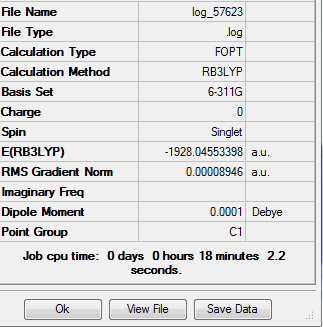
The three isomers cannot be compared by the resultant energy from the optimisation calculation because they are based on different elements.
The organometallic Ni-C bond lengths are summarised as follows:
| Complex | Ni-C bond length (Å) | Substituint Electronegativity (Pauling scale) |
| Trans-[Ni(CO)3(CBr3)2] | 2.03 | 2.96 |
| Trans-[Ni(CO)3(CCl3)2] | 2.05 | 3.16 |
| Trans-[Ni(CO)3(CH3)2] | 2.01 | 2.20 |
As expected, the Ni-C bond length increases with increasing electronegativity. This is due to the electron withdrawing effect which comes with a higher electronegativity resulting in a decrease of the carbon ligands ability to bond with its spare electron to the metal.
Vibrational Analysis
The vibrational analysis was carried out using the same B3LYP method and 6-311G basis set. The spectrums and symmetric carbonyl C=O stretches are summarised as follows:
| Complex | Spectrum | Carbonyl symmetric stretching frequency (cm-1) | Animation | Substituint Electronegativity (Pauling scale) |
| Trans-[Ni(CO)3(CCl3)2] |  |
2082 |  |
3.16 |
| Trans-[Ni(CO)3(CBr3)2] |  |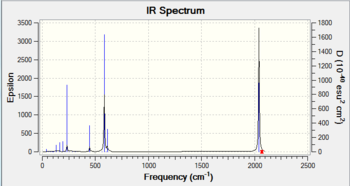
2069 |  |
2.96 |
| Trans-[Ni(CO)3(CH3)2] |  |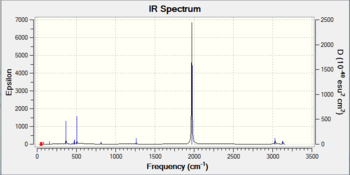
2021 |  |
2.2 |
As expected, the vibrational bond stretching frequency of the C=O bond increases with increasing electronegativity, because of the electron withdrawing effect resulting in less donation of electron density from the organometallic carbon based ligand to the metal centre. The metal centre therefore has less electron density, there is less back bonding to the carbonyl ligands and a stronger C=O bond.
References
- ↑ J. Chem. Phys. 96, 3411 (1992); http://dx.doi.org/10.1063/1.461942
- ↑ J. Am. Chem. Soc., 1994, 116 (11), pp 4970–4976; http://dx.doi.org/10.1021/ja00090a048
- ↑ http://hdl.handle.net/10042/to-13199
- ↑ J. Am. Chem. Soc., 1995, 117 (18), pp 5089–51; http://dx.doi.org/10.1021/ja00123a011